Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

ijkl

with any permutation of a given set ijkl are equal. Note that G

ijkl

has more

symmetries than the elastic compliance tensor. For isotropic symmetry, the elements

of G

ijkl

are given by the Table 6.14.1.

Table 6.14.1 gives exactly the same result as the isotropic equations of Mavko and

Jizba (1991) presented in Section 6.10.

When the rock is transversely isotropic with the 3-axis as the axis of rotational

symmetry, the five independent components of G

ijkl

are

1111

¼

ðdryÞ

1111



1  4a



ðdryÞ

1122

þ 

ðdryÞ

1133

1122



ðdryÞ

1122

1  4a

1133



ðdryÞ

1133

1  4a

3333

¼

ðdryÞ

3333



8a

ðdryÞ

1133

1  4a

2323



ðdryÞ

2323

1  4a





ðdryÞ

1111

þ 

ðdryÞ

3333

4ð1  4aÞ

1111

þ G

3333

The nine independent components of G

ijkl

for orthorhombic symmetry are

1111

¼

ðdryÞ

1111



1  4a



ðdryÞ

1122

þ 

ðdryÞ

1133

2222

¼

ðdryÞ

2222



1  4a



ðdryÞ

1122

þ 

ðdryÞ

2233

3333

¼

ðdryÞ

3333



1  4a



ðdryÞ

1133

þ 

ðdryÞ

2233

1122



ðdryÞ

1122

1  4a

Table 6.14.1 Elements of the tensor G

ijkl

for isotropic symmetry.

ij 11 22 33 23 13 12

11 1/5 1/15 1/15 0 0 0

22 1/15 1/5 1/15 0 0 0

33 1/15 1/15 1/5 0 0 0

23 0 0 0 1/15 0 0

13 00001/15 0

12 000001/15

307 6.14 Anisotropic squirt

1133



ðdryÞ

1133

1  4a

2233



ðdryÞ

2233

1  4a

2323



ðdryÞ

2323

1  4a





ðdryÞ

2222

þ 

ðdryÞ

3333

4ð1  4aÞ

2222

þ G

3333

1313



ðdryÞ

1313

1  4a





ðdryÞ

1111

þ 

ðdryÞ

3333

4ð1  4aÞ

1111

þ G

3333

1212



ðdryÞ

1212

1  4a





ðdryÞ

1111

þ 

ðdryÞ

2222

4ð1  4aÞ

1111

þ G

2222

where



ðdryÞ

ijkl

S

ðdryÞ

ijkl

S

ðdryÞ

ggbb

a ¼

ð

ðdryÞ

gbgb

 1Þ

Computed from the dry data, a is the ratio of the representative shear-to-normal

compliance of a crack set, including all elastic interactions with other cracks. When

the orthorhombic anisotropy is due to three mutually perpendicular crack sets,

superposed on a general orthorhombic background, with the crack normals along

the three symmetry axes, the wet-frame compliances are obtained from

ðdryÞ

ijkl

 S

ðwetÞ

ijkl



S

ðdryÞ

1111

1 þ 

ð1Þ

soft

ðb

 b

Þ=S

ðdryÞ

1111

S

ðdryÞ

2222

1 þ 

ð2Þ

soft

ðb

 b

Þ=S

ðdryÞ

2222

S

ðdryÞ

3333

1 þ 

ð3Þ

soft

ðb

 b

Þ=S

ðdryÞ

3333

where d

is the Kronecker delta, and 

ðiÞ

soft

refers to the soft porosity caused by the ith

crack set. The above expressions assume that the intrinsic compliance tensor of planar

crack-like features is sparse, the largest components being the normal and shear

compliances, whereas the other components are approximately zero. This general

property of planar crack formulations reflects an approximate decoupling of normal

and shear deformation of the crack and decoupling of the in-plane and out-of-plane

compressive deformation. In the case of a single crack set (with crack normals along

308 Fluid effects on wave propagation

the 3-axis) the wet-frame compliances can be calculated from the dry compliances for

a completely general, nonsparse crack compliance as

ðwetÞ

ijkl

¼ S

ðdryÞ

ijkl



S

ðdryÞ

llij

S

ðdryÞ

kl

S

ðdryÞ

g gdd

þ 

soft

ðb

 b

Little or no change of the S

ðdryÞ

1111

and S

ðdryÞ

2222

dry compliances with stress would

indicate that all the soft, crack-like porosity is aligned normal to the 3-axis. However,

a rotationally symmetric distribution of cracks may often be a better model of crack-

induced transversely isotropic rocks than just a single set of aligned cracks. In this

case the equations in terms of G

ijkl

should be used.

The anisotropic squirt formulation presented here does not assume any idealized

crack geometries. Because the high-frequency saturated compliances are predicted

entirely in terms of the measured dry compliances, the formulation automatically

incorporates all elastic pore interactions, and there is no limitation to low crack density.

Although the formulation presented here is independent of any idealized crack

shape, the squirt behavior is also implicit in virtually all published formulations for

effective moduli based on elliptical cracks (see Sections 4.7–4.11). In most of those

models, the cavities are treated as isolated with respect to flow, thus simulating the

high-frequency limit of the squirt model.

Uses

The anisotropic squirt formulation can be used to calculate high-frequency, saturated-

rock velocities from dry-rock velocities.

Assumptions and limitations

The use of the anisotropic squirt formulation requires the following considerations:



high seismic frequencies ideally suited for ultrasonic laboratory measurements are

assumed. In-situ seismic velocities will generally have neither squirt nor Biot disper-

sion and should be described by using Brown and Korringa equations. Sonic-logging

frequencies may or may not be within the range of validity, depending on the rock

type and fluid viscosity;



all minerals making up rock have the same compliances; and



fluid-bearing rock is completely saturated.

Extensions

The following extensions of the anisotropic squirt formulation can be made:



for mixed mineralogy, one can usually use an effective average modulus for b

;



for clay-filled rocks, it often works best to consider the “soft” clay to be part of the

pore-filling phase rather than part of the mineral matrix. The pore fluid is then

“mud,” and its modulus can be estimated with an isostress calculation.

309 6.14 Anisotropic squirt

6.15 Common features of fluid-related velocity dispersion

mechanisms

Synopsis

Many physical mechanisms have been proposed and modeled to explain velocity

dispersion and attenuation in rocks: scattering (see Section 3.14), viscous and inertial

fluid effects (see Sections 6.1, 6.2,and6.10–6.19), hysteresis related to surface forces,

thermoelastic effects, phase changes, and so forth. Scattering and surface forces appear

to dominate in dry or nearly dry conditions (Tutuncu, 1992; Sharma and Tutuncu,

1994). Viscous fluid mechanisms dominate when there is more than a trace of pore

fluids, such as in the case of the poroelasticity described by Biot (1956)andthelocal

flow or squirt mechanism (Stoll and Bryan, 1970;MavkoandNur,1975; O’Connell and

Budiansky, 1977; Stoll, 1989; Dvorkin and Nur, 1993). Extensive reviews of these were

given by Knopoff (1964), Mavko, Kjartansson, and Winkler (1979), and Bourbie

et al.

(1987), among others. Extensive reviews of these were given by Winkler (1985, 1986).

This section highlights some features that attenuation–dispersion models have in

common. These suggest a simple approach to analyzing dispersion, bypassing some

of the complexity of the individual theories, complexity that is often not warranted

by available data.

Although the various dispersion mechanisms and their mathematical descriptions are

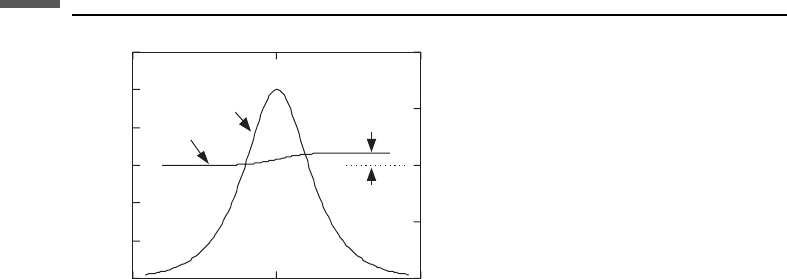
distinct, most can be described by the following three key parameters (see Figure 6.15.1):

1. a low-frequency limiting velocity V

(or modulus, M

) often referred to as the

“relaxed” state;

2. a high-frequency limiting velocity V

(or modulus, M

) referred to as the

“unrelaxed” state;

3. a characteristic frequency, f

, that separates high-frequency behavior from low-

frequency behavior and specifies the range in which velocity changes most rapidly.

High- and low-frequency limits

Of the three key parameters, usually the low- and high-frequency limits can be

estimated most easily. These require the fewest assumptions about the rock micro-

geometry and are, therefore, the most robust. In rocks, the velocity (or modulus)

generally increases with frequency (though not necessarily monotonically in the case

of scattering), and thus M

> M

. The total amount of dispersion between very

low-frequency and very high-frequency (M

– M

)/M ¼DM/M is referred to as the

modulus defect (Zener, 1948), where M ¼

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

One of the first steps in analyzing any dispersion mechanism should be to estimate

the modulus defect to see whether the effect is large enough to warrant any additional

modeling. In most situations all but one or two mechanisms can be eliminated based

on the size of the modulus defect alone.

310 Fluid effects on wave propagation

As an example, consider the local flow or squirt mechanism, which is discussed in

Sections 6.10–6.14 and 6.17. The squirt model recognizes that natural heterogeneities

in pore stiffnessess, pore orientation, fluid compressibility, and saturation can cause

spatial variations in wave-induced pore pressures at the pore scale. At sufficiently low

frequencies, there is time for the fluid to flow and eliminate these variations; hence,

the very low-frequency limiting bulk and shear moduli can be predicted by Gassmann’s

theory (Section 6.3), or by Brown and Korringa’s theory (Section 6.5)iftherockis

anisotropic. At high frequencies, the pore-pressure variations persist, causing the rock

to be stiffer. The high-frequency limiting moduli may be estimated from dry-rock data

using the Mavko and Jizba method (Section 6.10). These low- and high-frequency

limits are relatively easy to estimate and require minimum assumptions about pore

microgeometry. In contrast, calculating the detailed frequency variation between

the low- and high-frequency regimes requires estimates of the pore aspect-ratio or

throat-size distributions.

Other simple estimates of the high- and low-frequency limits associated with the

squirt mechanism can be made by using ellipsoidal crack models such as the Kuster

and Tokso

z model (Section 4.7), the self-consistent model (Section 4.8), the DEM

model (Section 4.9), or Hudson’s model (Section 4.10). In each case, the dry rock is

modeled by setting the inclusion moduli to zero. The high-frequency saturated rock

conditions are simulated by assigning fluid moduli to the inclusions. Because each

model treats the cavities as isolated with respect to flow, this yields the unrelaxed

moduli for squirt. The low-frequency saturated moduli are found by taking the model-

predicted effective moduli for dry cavities and saturating them with the Gassmann

low-frequency relations (see Section 6.3).

The characteristic frequency is also simple to estimate for most models but

usually depends more on poorly determined details of grain and pore microgeometry.

Hence, the estimated critical frequency is usually less robust. Table 6.15.1 summarizes

0.1

0.2

0.3

0.4

0.5

0.6

0.5

1.5

−50 5

1/Q (∆M/M)

Modulus (M/M

)

log(f

/f )

1/Q

∆M

∞

Figure 6.15.1 Key parameters in various dispersion mechanisms: M

, the low-frequency limiting

modulus, M

, the high-frequency limiting modulus, and f

, the characteristic frequency separating

high- and low-frequency behavior.

311 6.15 Common features of fluid-related velocity dispersion

Table 6.15.1 High- and low-frequency limits and characteristic frequency of dispersion mechanisms.

Mechanism

Low-frequency limit

High-frequency limit

Characteristic frequency (f

)

Biot [6.1] Gassmann’s relations [6.3] Biot’s high-frequency formula [6.1] f

Biot

 f/2pr

Squirt [6.10–6.14]

b Gassmann’s relations [6.3] Mavko–Jizba relations [6.10] f

squirt

 K

/

c Kuster–Tokso

z dry relations [4.7] ! Gassmann Kuster–Tokso

z saturated relations ”

c DEM dry relations [4.9] ! Gassmann DEM saturated relations ”

c Self-consistent dry relations [4.8] ! Gassmann Self-consistent saturated relations ”

d Hudson’s dry relations [4.10] ! Brown and Korringa [6.5] Hudson’s saturated relations ”

Patchy saturation [6.17, 6.18]

e Gassmann’s relations [6.3] Hill equation [4.5] f

patchy

 k/L

(b

þ b

)

f Gassmann’s relations [6.3] White high-frequency formula [6.18] f

patchy

 kK

/pL



g Generalized Gassmann’s relations [6.6] Dutta–Ode

high-frequency formula [6.18] ”

Viscous shear

Scattering [3.10–3.14]

hhf

visc.crack

 am/2p

i Effective medium theory [4.1–4.15] Ray theory [3.11–3.13] f

scatter

 V/2pa

j Backus average [4.13] Time average [3.11–3.13] ”

Numbers in brackets [ ] refer to sections in this book.

Inputs are measured dry-rock moduli; no idealized pore geometry.

Pore space is modeled as idealized ellipsoidal cracks.

Anisotropic rock modeled as idealized penny-shaped cracks with preferred orientations.

Dry rock is homogeneous; saturation has arbitrarily shaped patches.

Dry rock is homogeneous; saturation is in spherical patches. Same limits as

Dry rock can be heterogeneous; saturation is in spherical patches.

The mechanism modeled by Walsh (1969) is related to shearing of penny-shaped cracks with viscous fluids. Interesting only for extremely high viscosity or extremely high

frequency.

General heterogeneous three-dimensional medium.

Normal-incidence propagation through a layered medium.

f ¼ porosity, L ¼ characteristic size (or correlation length), K

, m ¼ bulk and shear moduli of mineral of saturation heterogeneity, K

¼ saturated rock modulus, r

¼ density

of the pore fluid, b

¼ compressibility of the pore fluid,  ¼ viscosity of the pore fluid, b

¼ compressibility of the pore space, a ¼ pore aspect ratio, a ¼ characteristic size

(or correlation length) of scatterers, k ¼ rock permeability, V ¼ wave velocity at f

approaches to estimating the low-frequency moduli, high-frequency moduli, and char-

acteristic frequencies for five important categories of velocity dispersion and attenuation.

Each mechanism shown in the table has an f

value that depends on poorly determined

parameters. The Biot (see Section 6.1)andpatchy(seeSection 6.17) models depend on

the permeability. The squirt (see Sections 6.10–6.14) and viscous shear (Walsh, 1969)

models require the crack aspect ratio. Furthermore, the formula for f

–squirt is only a

rough approximation, for the dependence on a

is of unknown reliability. The patchy-

saturation (see Section 6.17) and scattering (see Sections 3.10–3.14) models depend on

the scale of saturation and scattering heterogeneities. Unlike the other parameters, which

are determined by grain and pore size, saturation and scattering can involve all scales,

ranging from the pore scale to the basin scale.

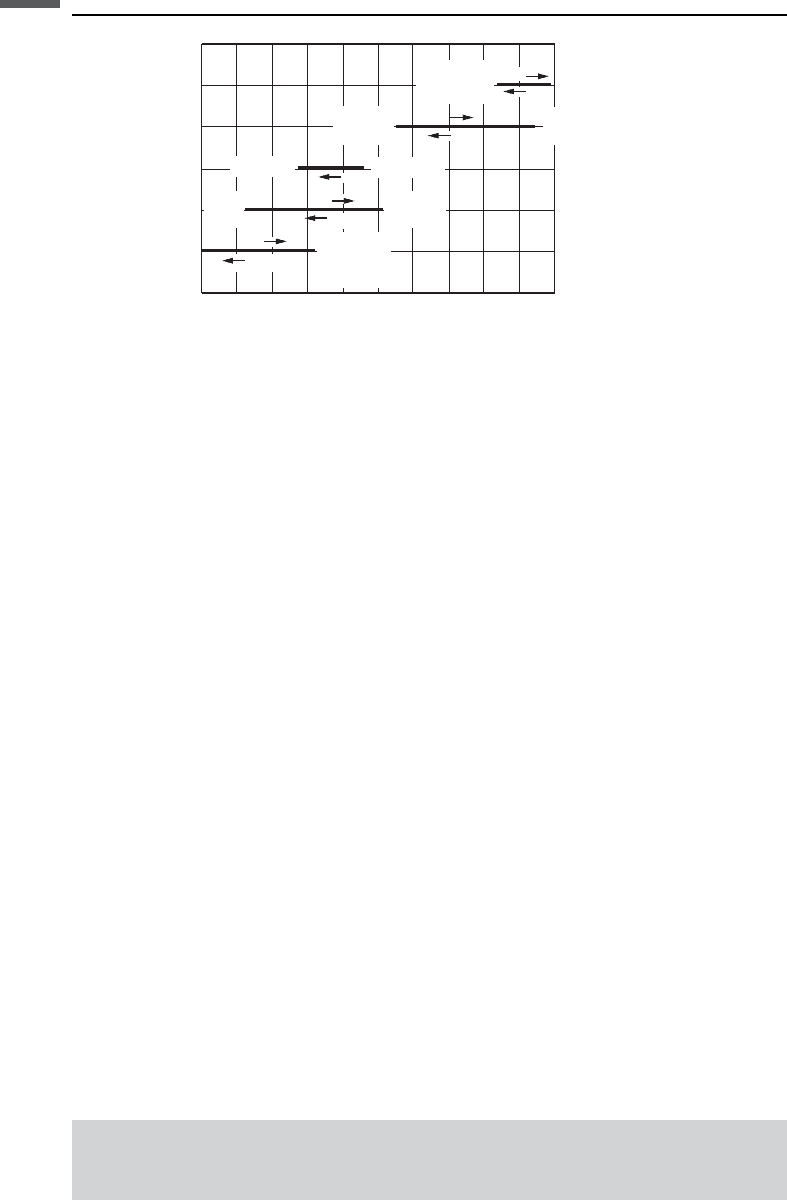
Figure 6.15.2 compares some values for f

predicted by the various expressions in

the table. The following parameters (or ranges of parameters) were used:

f ¼0.2 ¼porosity

¼1.0 g/cm

¼fluid density

 ¼1–10 cP ¼fluid viscosity

k ¼1–1000 mD ¼permeability

a ¼10

–3

–10

–4

¼crack aspect ratio

V ¼3500 m/s ¼wave velocity

a, L ¼0.1–10 m ¼characteristic scale of heterogeneity

m ¼17 GPa ¼rock shear modulus

K ¼18 GPa ¼rock bulk modulus

Caution

Other values for rock and fluid parameters can change f

considerably.

−1

Critical frequency f

(Hz)

Biot

Squirt

Patchy saturation

Viscous shear

Scattering

a =10

−4

a =10

−3

a =10

−4

h = 10 cP

h = 1 cP

k = 1 mD

k =1 D

a = 10 m

a = 0.1 m

L = 0.1 m

h,L

Figure 6.15.2 Comparison of characteristic frequencies for typical rock and fluid parameters.

Arrows show the direction of change as the labeled parameter increases.

313 6.15 Common features of fluid-related velocity dispersion

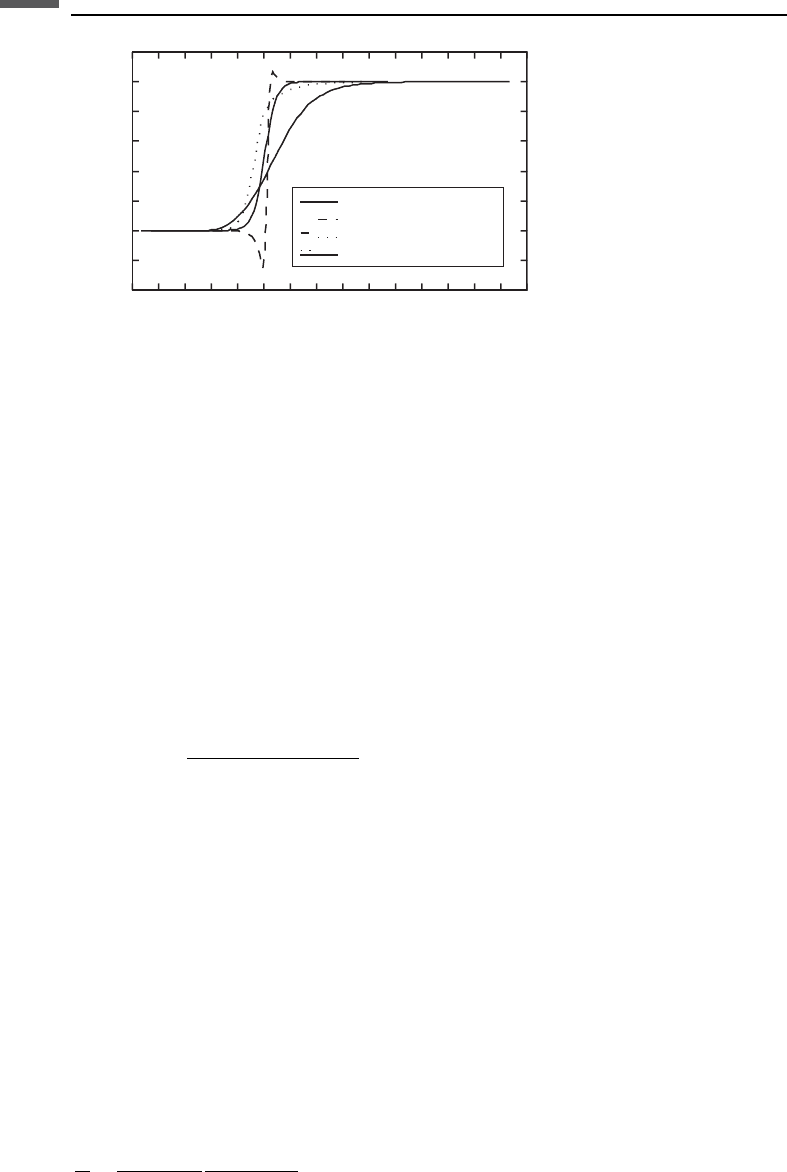
Complete frequency dependence

Figure 6.15.3 compares the complete normalized velocity-versus-frequency depend-

ence predicted by the Biot, patchy-saturation, and scattering models. Although there are

differences, each follows roughly the same trend from the low-frequency limits to the

high-frequency limits, and the most rapid transition is in the range f  f

. This is not

always strictly true for the Biot mechanism, where certain combinations of parameters

can cause the transition to occur at frequencies far from f

Biot

. All are qualitatively

similar to the dispersion predicted by the standard linear solid (see Section 3.8):

ReðMðo ÞÞ ¼

1 þ f =f

ðÞ

þ f =f

ðÞ

Because the value of f

and the resulting curves depend on poorly determined

parameters, we suggest that a simple and practical way to estimate dispersion curves

is to use the standard linear solid. The uncertainty in the rock microgeometry,

permeability, and heterogeneous scales – as well as the approximations in the theories

themselves – often makes a more detailed analysis unwarranted.

Attenuation

The Kramers–Kronig relations (see Section 3.9) completely specify the relation

between velocity dispersion and attenuation. If velocity is known for all frequencies,

then attenuation is determined for all frequencies. The attenuation versus frequency

for the standard linear solid is given by

 M

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

f =f

1 þ f =f

ðÞ

−0.4

−0.2

0.0

0.2

0.4

0.6

0.8

1.0

1.2

−5

−3

0.1 10 10

Biot dispersion

Scattering dispersion

Patchy dispersion

Standard linear solid

f /f

(V − V

)/(V

∞

− V

)

Figure 6.15.3 Comparison of the complete normalized velocity-versus-frequency dependence

predicted by the Biot, patchy-saturation, and scattering models.

314 Fluid effects on wave propagation

Similarly, it can be argued (see Section 3.8) that, in general, the order of magnitude of

attenuation can be determined from the modulus defect:



 M

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

Uses

The preceding simplified relations can be used to estimate velocity dispersion and

attenuation in rocks.

Assumptions and limitations

This discussion is based on the premise that difficulties in measuring attenuation and

velocity dispersion, and in estimating aspect ratios, permeability, and heterogeneous

scales, often make detailed analysis of dispersion unwarranted. Fortunately, much

about attenuation–dispersion behavior can be estimated robustly from the high- and

low-frequency limits and the characteristic frequency of each physical mechanism.

6.16 Dvorkin–Mavko attenuation model

Synopsis

Dvorkin and Mavko (2006) present a theory for calculating the P- and S-wave

inverse quality factors (Q

1

and Q

1

, respectively) at partial and full saturation. The

basis for the quality factor estimation is the standard linear solid (SLS) model

(Section 3.8) that links the inverse quality factor Q

1

to the corresponding elastic

modulus M versus frequency f dispersion as

1

ðf Þ¼

ðM

 M

Þðf =f

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

½1 þðf =f



where M

and M

are the low- and high-frequency limits of the modulus M,

respectively; and f

is the critical frequency at which the inverse quality factor is

maximum.

Partial water saturation

Consider rock in which K

dry

is the bulk modulus of the dry frame of the rock; K

mineral

is the bulk modulus of the mineral phase; and f is the total porosity. Its bulk modulus

at partial water saturation S

is (according to Gassmann’s equation)

¼ K

mineral

K

dry

ð1 þ ÞK

dry

mineral

þ K

ð1  ÞK

þ K

mineral

 K

dry

mineral

315 6.16 Dvorkin–Mavko attenuation model

where K

is the bulk modulus of the pore fluid which is a uniform mixture of water

with the bulk modulus K

and hydrocarbon (e.g., gas) with the bulk modulus K

1  S

Then the compressional modulus M

is obtained from K

and the shear modulus of

the dry frame m

dry

¼ K

dry

Alternatively, to obtain M

, one may use the approximate V

-only fluid-substitution

equation with the dry-frame compressional modulus M

dry

and the mineral-phase

compressional modulus M

mineral

¼ M

mineral

M

dry

ð1 þ ÞK

dry

mineral

þ K

ð1  ÞK

þ M

mineral

 K

dry

mineral

The compressional modulus M

thus obtained (either by Gassmann’s equation or V

only fluid-substitution) is considered the low-frequency limit of the compressional

modulus M.

The high-frequency limit of the compressional modulus M

is calculated using the

patchy-saturation equations (Section 6.17). It is assumed that the difference between

and M

is nonzero only at water saturation larger than the irreducible water

saturation S

irr

. For S

 S

irr

, M

¼ M

, i.e., Q

1

¼ 0.

For S

> S

irr

dry

ðS

 S

irr

Þ=ð1  S

irr

dry

ð1  S

Þ=ð1  S

irr

mineral

irr

dry

where

¼ K

mineral

K

dry

ð1 þ ÞK

dry

mineral

þ K

ð1  ÞK

þ K

mineral

 K

dry

mineral

irr

¼ K

mineral

K

dry

ð1 þ ÞK

irr

dry

mineral

þ K

irr

ð1  ÞK

irr

þ K

mineral

 K

irr

dry

mineral

irr

1  S

irr

Then the high-frequency limit of the compressional modulus M

¼ K

dry

and the inverse P-wave quality factor Q

1

is calculated from the SLS dispersion

equation as presented at the beginning of this section.

316 Fluid effects on wave propagation