Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

Assumptions and limitations

The preceding relations have the following limitations:



these relations are empirical and thus, strictly speaking, they apply only to the

set of rocks studied. However, the result should extend in general to many

consolidated sandstones. In any case, the key result is that clay content is an

important parameter for quantifying velocity; if possible, the regression coeffi-

cients should be recalibrated from core s or logs at the site being studied, but be

sure to include clay;



Han’s linear regression coefficients change slightly with confining pressure. They

are fairly stable above about 10 MPa; below this, they vary more, and the correl-

ation coefficients degrade;



a common mistake is to try to overinterpret the empirical coefficients by

comparing the equations, for example, to Wyllie’s time-average equation (see

Section 7.3). This can lead to nonsensical interpreted values for the velocities

of water and clay. This is not surprising, for Wyllie’s equations are only

heuristic and;



it is dangerous to extrapolate the results to values of porosity or clay content outside

the range of the experiments. Note, for example, that the intercepts of the various

equations corresponding to no porosity and no clay do not agree with each other

and generally do not agree with the velocities in pure quartz.

7.6 Velocity–porosity–clay models: Tosaya’s empirical relations for

shaley sandstones

Synopsis

On the basis of their measurements, Tosaya and Nur (1982) determined empirical

regressions relating ultrasonic (laboratory) P- and S-wave velocities to porosity and

clay content. For water-saturated rocks at an effective pressure of 40 MPa, they found

ðkm=sÞ¼5:8  8:6  2:4C

ðkm=sÞ¼3:7  6:3  2:1C

where f is the porosity and C is the clay content by volume. See also Han’s relation

in Section 7.5.

Uses

Tosaya’s relations can be used to relate velocity, porosity, and clay content empiric-

ally in shaley sandstones.

357 7.6 Tosaya’s empirical relations for shaley sandstones

Assumptions and limitations

Tosaya’s relations have the following limitations:



these relations are empirical, and thus strictly speaking they apply only to the set

of rocks studied. However, the result should extend in general to many consoli-

dated sandstones. In any case, the key result is that clay content is an important

parameter for quantifying velocity; if possible, the regression coefficients should

be recalibrated from cores or logs at the site being studied, but be sure to

include clay;



the relation given above holds only for the high effective pressure value of 40 MPa.



a common mistake is to try to overinterpret the empirical coefficients by comparing

the equations, for example, to Wyllie’s time-average equation (see Section 7.3).

This can lead to nonsensical interpreted values for the velocities of water and clay.

This is not surprising, because Wyllie’s equations are heuristic only; and



it is dangerous to extrapolate the results to values of porosity or clay content outside

the range of the experiments.

7.7 Velocity–porosity–clay models: Castagna’s empirical relations

for velocities

Synopsis

On the basis of log measurements, Castagna et al. (1985) determined empirical

regressions relating velocities with porosity and clay content under water-saturated

conditions. See also Section 7.9 on V

–V

relations.

For mudrock (clastic silicate rock composed primarily of clay and silt-sized

particles), they found the relation between V

and V

(in km/s) to be

ðkm=sÞ¼1:36 þ 1:16V

where V

and V

are the P- and S-wave velocities, respectively.

For shaley sands of the Frio formation they found

ðkm=sÞ¼5:81  9:42  2:21C

ðkm=sÞ¼3:89  7:07  2:04C

where f is porosity and C is the clay volume fraction.

Uses

Castagna’s relations for velocities can be used to relate velocity, porosity, and clay

content empirically in shaley sandstones.

358 Empirical relations

Assumptions and limitations

Castagna’s empirical relations have the following limitations:



these relations are empirical, and thus strictly speaking they apply only to the set of

rocks studied;



a common mistake is to try to overinterpret the empirical coefficients by comparing

the equations, for example, to Wyllie’s time-average equation (see Section 7.3).

This can lead to nonsensical interpreted values for the velocities of water and clay.

This is not surprising because Wyllie’s equations are heuristic only; there is no

theoretical justification for them, and they do not represent an empirical best fit to

any data.

7.8 V

–V

–density models: Brocher’s compilation

Synopsis

Brocher (2005) compiled data on crustal rocks from the laboratory, wireline logs,

VSP (vertical seismic profiling), and field tomography, from which he found empir-

ical relations among V

, V

, bulk density (r), and Poisson’s ratio (n) for crustal rocks.

The data represented a broad range of lithologies, including sandstones, shales,

mafics, gabbros, calcium-rich rocks (dolomites and anorthosite), and other crystalline

rocks. The resulting empirical relations are intended to represent the average behavior

of crustal rocks over a large depth range. Brocher compared his results with an

excellent compilation of other published empirical relations, which are summarized

in this section.

–density

Brocher (2005) computed the following polynomial fit to the Nafe–Drake curve

(Ludwig et al., 1970) relating P-wave velocity and bulk density, previously presented

only graphically:

 g=cm



¼ 1:6612V

km=sðÞ0:4721V

þ 0:0671V

 0:0043V

þ 0:000 106 V

ð7:8:1Þ

Equation (7.8.1) is intended for velocities in the range 1:5 < V

< 8:5km=s and all

crustal rocks, except crustal mafic and calcium-rich rocks. Brocher also presented an

inverse relation

359 7.8 V

–V

–density models: Brocher’s compilation

km=s

ðÞ

¼ 39:128 g=cm



 63:064

þ 37:083

 9:1819

þ 0:8228

ð7:8:2Þ

which is accurate in the density range 2:0 <<3:5g=cm

. Equations (7.8.1) and

(7.8.2) can be compared with an equation from Gardner et al. (1974) for sedimentary

rocks:

 g=cm



¼ 1:74V

0:25

ð7:8:3Þ

which is valid for velocities in the range 1:5 < V

< 6:1.

Christensen and Mooney (1995) published a relation between P-wave velocity and

bulk density in crystalline rocks at 10 km depth (except for volcanic and monomi-

neralic rocks) and in the range 5:5 < V

< 7:5:

 g=cm



¼ 0:541 þ 0:360V

ð7:8:4Þ

Godfrey et al. (1997) proposed a linear relation for basalt, diabase, and gabbro, based

on data reported by Christensen and Mooney (1995):

 g=cm



¼ 2:4372 þ 0:0761V

ð7:8:5Þ

Equation (7.8.5) is also intended for crustal rocks at 10 km depth in the velocity

range 5:9 < V

< 7:1.

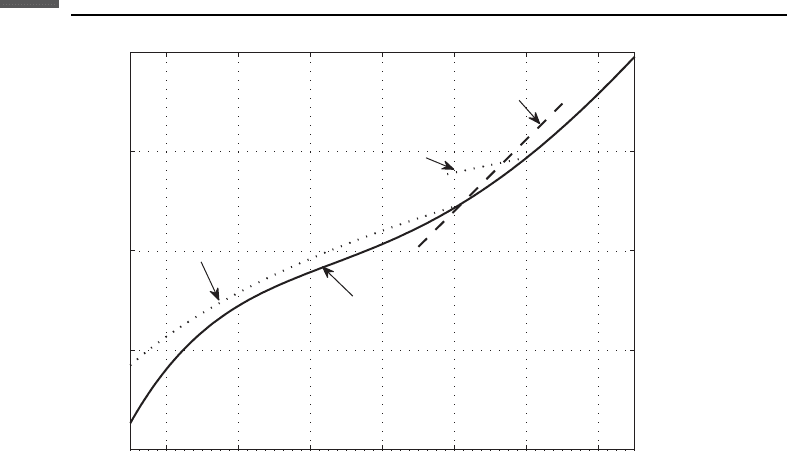
Equations (7.8.1) and (7.8.3)–(7.8.5) are compared in Figure 7.8.1.

2 3 4 5 6 7 8

1.5

2.5

3.5

(km/s)

Density (g/cm

)

Nafe–Drake (Eq. 1)

Gardner et al.

(Eq. 3)

Christensen and

Mooney (Eq. 4)

Godfrey et al.

Basalts, diabase, gabbro

(Eq. 5)

Figure 7.8.1 Brocher’s comparison of empirical V

-bulk density trends for crustal rocks,

equations (7.8.1), (7.8.3)–(7.8.5).

360 Empirical relations

–V

Brocher (2005) derived the following expression relating V

and V

in a broad range

of lithologies (excluding calcium-rich and mafic rocks, gabbros, and serpentinites),

using data from Ludwig et al. (1970):

km=sðÞ¼0:7858  1:2344V

þ 0:7949V

 0:1238V

þ 0:0064V

ð7:8:6Þ

Equation (7.8.6) is accurate for velocities in the range 1:5 < V

< 8:0km=s. The

inverse is given as

km=sðÞ¼0:9409 þ 2:0947V

 0:8206V

þ 0:2683V

 0:0251V

ð7:8:7Þ

Brocher’s relation, intended more specifically for calcium-rich (dolomites and

anorthosites), mafic rocks, and gabbros, labeled the “mafic line” in Figure 7.8.2,is

given by

km=sðÞ¼2:88 þ 0:52 V

 5:25ðÞ; 5:25 < V

< 7:25 ð7:8:8Þ

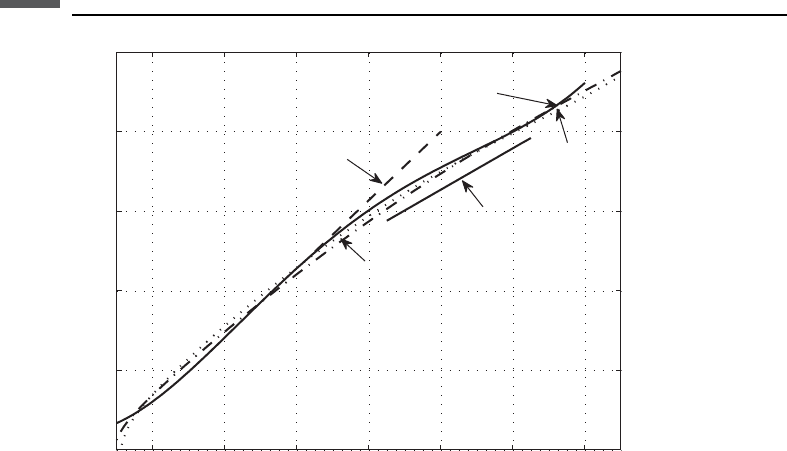
2345678

(km/s)

Brocher

regression (Eq. 6)

Mudrock (Eq. 9)

Mafic line (Eq. 8)

Brocher

empirical fit

(Eq. 10)

Ludwig

empirical fit

(Eq. 11)

Figure 7.8.2 Brocher’s comparison of empirical V

–V

trends for crustal rocks,

equations (7.8.6), (7.8.8)–(7.8.11).

361 7.8 V

–V

–density models: Brocher’s compilation

Equations (7.8.7) and (7.8.8) can be compared with the well-known mudrock line

of Castagna et al. (1985):

km=sðÞ¼V

 1:36ðÞ=1:16 ð7:8:9Þ

Figure 7.8.2 compares equations (7.8.6) and (7.8.8)–(7.8.11).

–Poisson’s ratio

Brocher (2005) computed the following equation, labeled “Brocher’s empirical fit,”

relating P-wave velocity and Poisson’s ratio, valid in the range, 1:5 < V

< 8:5:

 ¼ 0:8835  0:315V

þ 0:0491V

 0:0024V

ð7:8:10Þ

A similar relation, derived by Brocher from data by Ludwig et al. (1970), labeled

“Ludwig’s empirical fit,” is

 ¼ 0:769  0:226V

þ 0:0316V

 0:0014V

ð7:8:11Þ

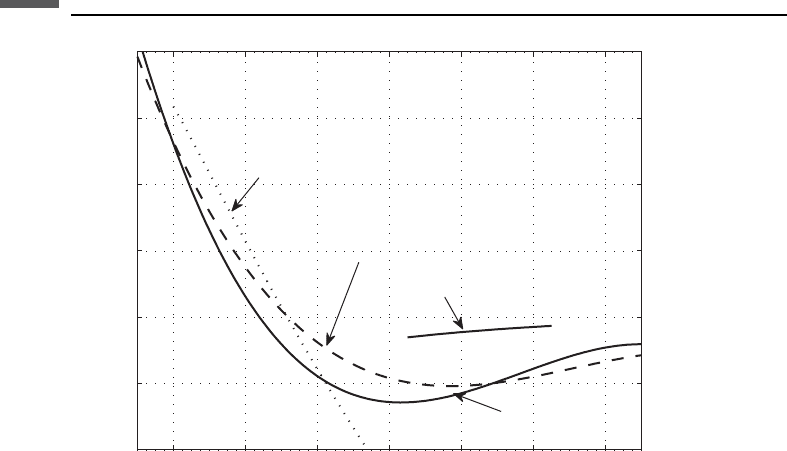
Equations (7.8.8)–(7.8.11) are compared in Figure 7.8.3.

Uses

These equations can be used to link V

, V

, and density in crustal rocks.

2 3 4 5 6 7 8

0.2

0.25

0.3

0.35

0.4

0.45

0.5

(km/s)

Poisson’s ratio

Mudrock (Eq. 9)

Mafic line (Eq. 8)

Brocher's

empirical fit

(Eq. 10)

Ludwig's

empirical fit (Eq. 11)

Figure 7.8.3 Brocher’s comparison of empirical V

–Poisson’s ratio trends for crustal rocks,

equations (7.8.8)–(7.8.11).

362 Empirical relations

Assumptions and limitations

The equations in this section are empirical. Many of them, particularly those of

Brocher, are intended to represent a broad range of crustal lithologies and depths.

Dependence of the relations on pore fluids is not shown; it can be assumed that these

represent water-saturated rocks.

7.9 V

–V

relations

Synopsis

–V

relations are key to the determination of lithology from seismic or sonic log

data as well as for direct seismic identification of pore fluids using, for example,

AVO analysis. Castagna et al. (1993) give an excellent review of the subject.

There is a wide and sometimes confusing variety of published V

–V

relations and

prediction techniques, which at first appear to be quite distinct. However, most

reduce to the same two simple steps.

1. Establish empirical relations among V

, V

, and porosity, f, for one reference pore

fluid – most often water-saturated or dry.

2. Use Gassmann’s (1951) relations to map these empirical relations to other pore-

fluid states (see Section 6.3).

Although some of the effective-medium models summarized in Chapter 4 predict

both P- and S-velocities on the basis of idealized pore geometries, the fact remains

that the most reliable and most often used V

–V

relations are empirical fits to

laboratory or log data, or both. The most useful role of theoretical methods is

extending these empirical relations to different pore fluids or measurement frequen-

cies, which accounts for the two steps listed above.

We summarize here a few of the popular V

–V

relations compared with laboratory

and log data sets and illustrate some of the variations that can result from lithology,

pore fluids, and measurement frequency.

Some empirical relations

Limestones

Figure 7.9.1 shows laboratory ultrasonic V

–V

data for water-saturated limestones

from Pickett (1963), Milholland et al. (1980), and Castagna et al. (1993), as compiled

by Castagna et al. (1993). Superimposed, for comparison, are Pickett’s (1963)

empirical limestone relation derived from laboratory core data:

¼ V

=1:9 ðkm=sÞ

and a least-squares polynomial fit to the data derived by Castagna et al. (1993):

¼0:055V

þ 1:017V

 1:031 ðkm=sÞ

363 7.9 V

–V

relations

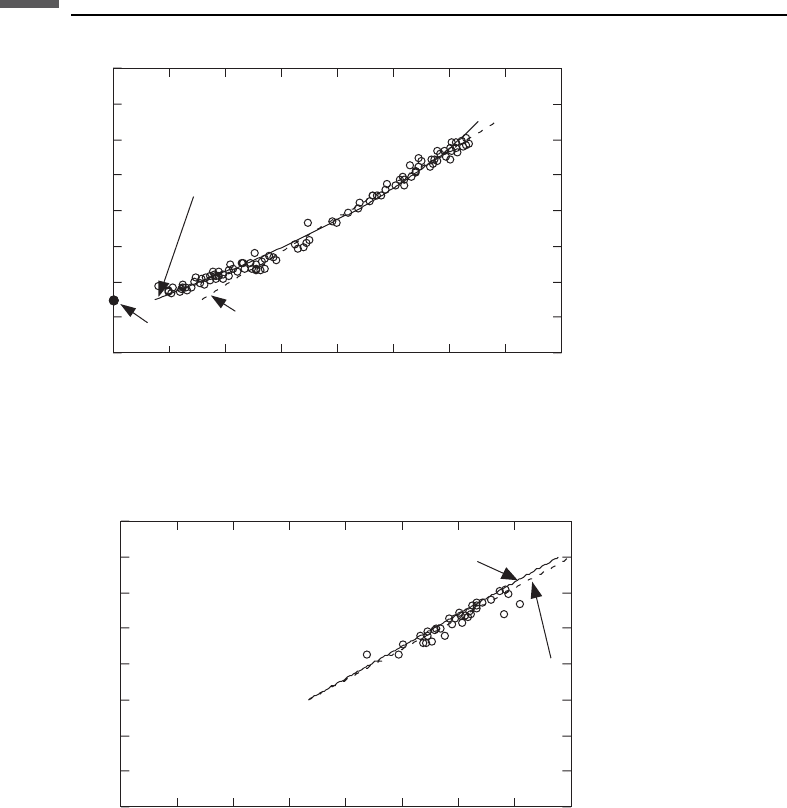
At higher velocities, Pickett’s straight line fits the data better, although at lower

velocities (higher porosities), the data deviate from a straight line and trend toward

the water point, V

¼ 1.5 km/s, V

¼ 0. In fact, this limit is more accurately described

as a suspension of grains in water at the critical porosity (see the discussion below), at

which the grains lose contact and the shear velocity vanishes.

Dolomite

Figure 7.9.2 shows laboratory V

–V

data for water-saturated dolomites from

Castagna et al. (1993). Superimposed, for comparison, are Pickett’s (1963) dolomite

(laboratory) relation

01234

Water-saturated dolomites

(km/s)

Castagna et al. (1993)

= 0.5832V

− 0.077 76

Pickett (1963)

= V

/1.8

(After Castagna et al., 1993)

Figure 7.9.2 Laboratory V

–V

data for water-saturated dolomites.

01234

Water-saturated limestones

(km/s)

= V

/1.9

Pickett (1963)

Castagna et al. (1993)

= −0.05508 V

+ 1.0168 V

−1.0305

Water

(After Castagna et al., 1993)

Figure 7.9.1 Laboratory ultrasonic V

–V

data for water-saturated limestones.

364 Empirical relations

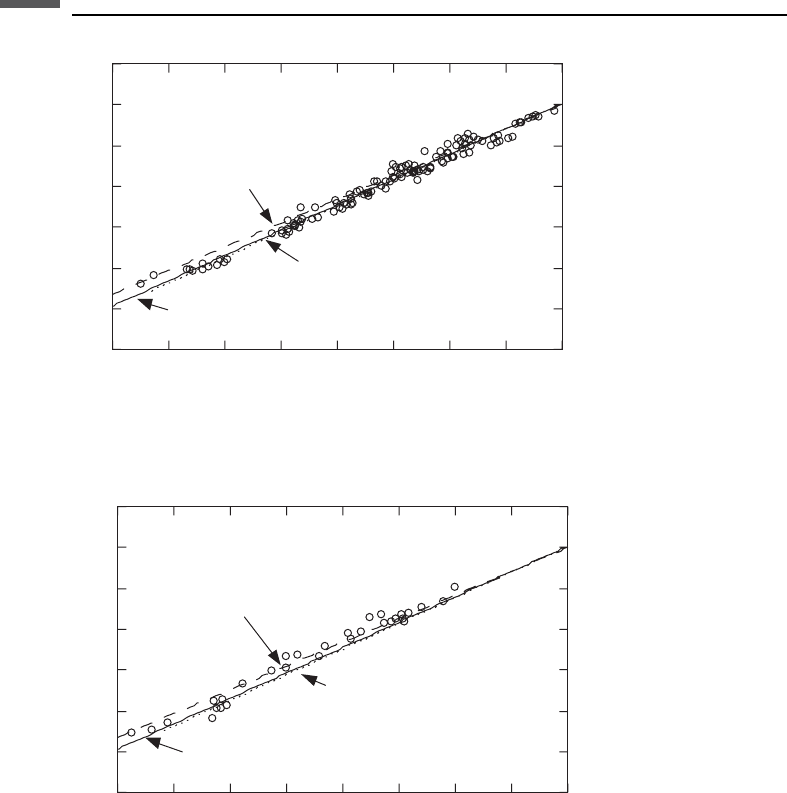
¼ V

=1:8 ðkm=sÞ

and a least-squares linear fit (Castagna et al., 1993)

¼ 0:583V

 0:078 ðkm=sÞ

For the data shown, the two relations are essentially equivalent. The data range is too

limited to speculate about behavior at much lower velocity (higher porosity).

Sandstones and shales

Figures 7.9.3 and 7.9.4 show laboratory V

–V

data for water-saturated sandstones

and shales from Castagna et al. (1985, 1993) and Thomsen (1986), as compiled by

01234

Water-saturated sandstones

(km/s)

Mudrock

= 0.8621V

−1.1724

Castagna et al. (1993)

= 0.8042V

−0.8559

Han (1986)

= 0.7936V

−0.7868

(After Castagna et al., 1993)

Figure 7.9.3 Laboratory V

–V

data for water-saturated sandstones.

01234

Water-saturated shales

(km/s)

Mudrock

= 0.8621 V

− 1.1724

Castagna et al. (1993)

= 0.8042V

− 0.8559

Han (1986)

= 0.7936V

− 0.7868

(After Castagna et al., 1993)

Figure 7.9.4 Laboratory V

–V

data for water-saturated shales.

365 7.9 V

–V

relations

Castagna et al. (1993). Superimposed, for comparison, are a least-squares linear fit to

these data offered by Castagna et al. (1993),

¼ 0:804V

 0:856 ðkm=sÞ

the famous “mudrock line” of Castagna et al. (1985), which was derived from in-situ

data,

¼ 0:862V

 1:172 ðkm=sÞ

and the following empirical relation of Han (1986), which is based on laboratory

ultrasonic data:

¼ 0:794V

 0:787 ðkm=sÞ

Of these three relations, those by Han (1986) and Castagna et al. (1985) are essen-

tially the same and give the best overall fit to the sandstones. The mudrock line

predicts systematically lower V

because it is best suited to the most shaley samples,

as seen in Figure 7.9.4. Castagna et al. (1993) suggest that if the lithology is well

known, one can fine tune these relations to slightly lower V

for high shale content

and higher V

in cleaner sands. When the lithology is not well constrained, the

Han and the Castagna et al. lines give a reasonable average.

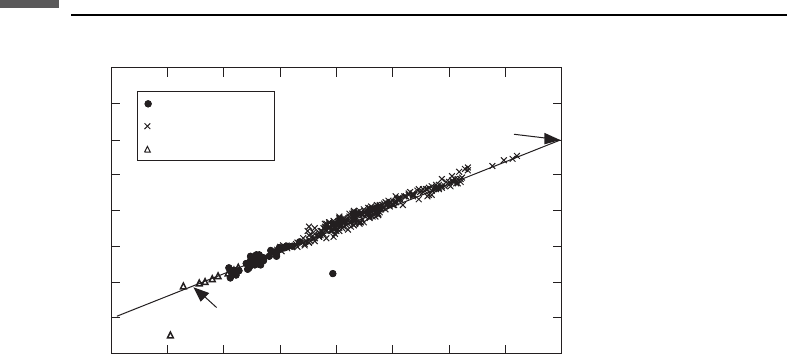
Figure 7.9.5 compares laboratory ultrasonic data for a larger set of water-saturated

sands. The lowest porosity samples (f ¼ 0.04–0.30) are from a set of consolidated

shaley Gulf Coast sandstones studied by Han (1986). The medium porosities (f ¼

0.22–0.36) are poorly consolidated North Sea samples studied by Blangy (1992). The

very-high-porosity samples (f ¼ 0.32–0.39) are unconsolidated clean Ottawa sand

studied by Yin (1992). The samples span clay volume fractions from 0% to 55%,

01234

Water-saturated shaley sands

f = 0.22–0.36

f = 0.04–0.30

f = 0.32–0.39

(km/s)

Quartz

= 0.79V

– 0.79

(Data from Han, Blangy, Yin)

Figure 7.9.5 Laboratory ultrasonic V

–V

data for water-saturated shaley sands.

366 Empirical relations