Mavko G., Mukerji T., Dvorkin J. The Rock Physics Handbook

Подождите немного. Документ загружается.

porosities from 0.04 to 0.39, and confining pressures from 0 to 40 MPa. In spite of this,

there is a remarkably systematic trend well represented by Han’s relation as follows:

¼ 0:79V

 0:79 ðkm=sÞ

Sandstones: more on the effects of clay

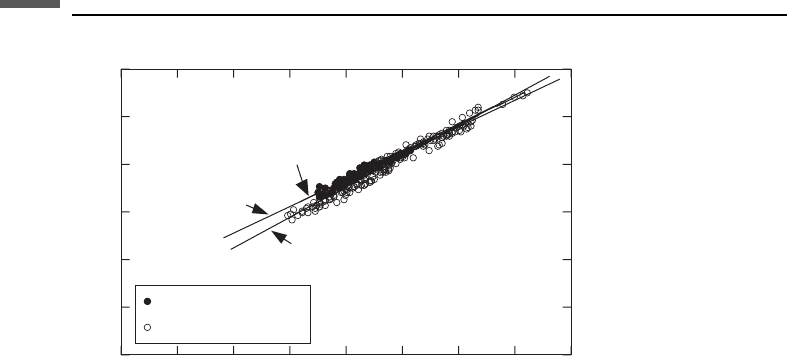
Figure 7.9.6 shows again the ultrasonic laboratory data for 70 water-saturated shaley

sandstone samples from Han (1986). The data are separated by clay volume fractions

greater than 25% and less than 25%. Regressions to each part of the data set are

shown as follows:

¼ 0:842V

 1:099; clay > 25%

¼ 0:754V

 0:657; clay < 25%

The mudrock line (upper line) is a reasonable fit to the trend but is skewed toward

higher clay and lies almost on top of the regression for clay >25%.

Sandstones: effects of porosity

Figure 7.9.7 shows the laboratory ultrasonic data for water-saturated shaley sand-

stones from Han (1986) separated into porosity greater than 15% and less than 15%.

Regressions to each part of the data set are shown as follows:

¼ 0:756V

 0:662; porosity > 15%

¼ 0:853V

 1:137; porosity < 15%

01234

Water-saturated shaley sandstones

P-sat

for clay > 25%

P-sat

for clay < 25%

(km/s)

Clay > 25%

= 0.8423V

−1.099

Clay < 25%

= 0.7535V

− 0.6566

Mudrock

= 0.8621V

− 1.1724

(Data from Han, 1986)

Figure 7.9.6 Laboratory ultrasonic V

–V

data for water-saturated shaley sands, differentiated

by clay content.

367 7.9 V

–V

relations

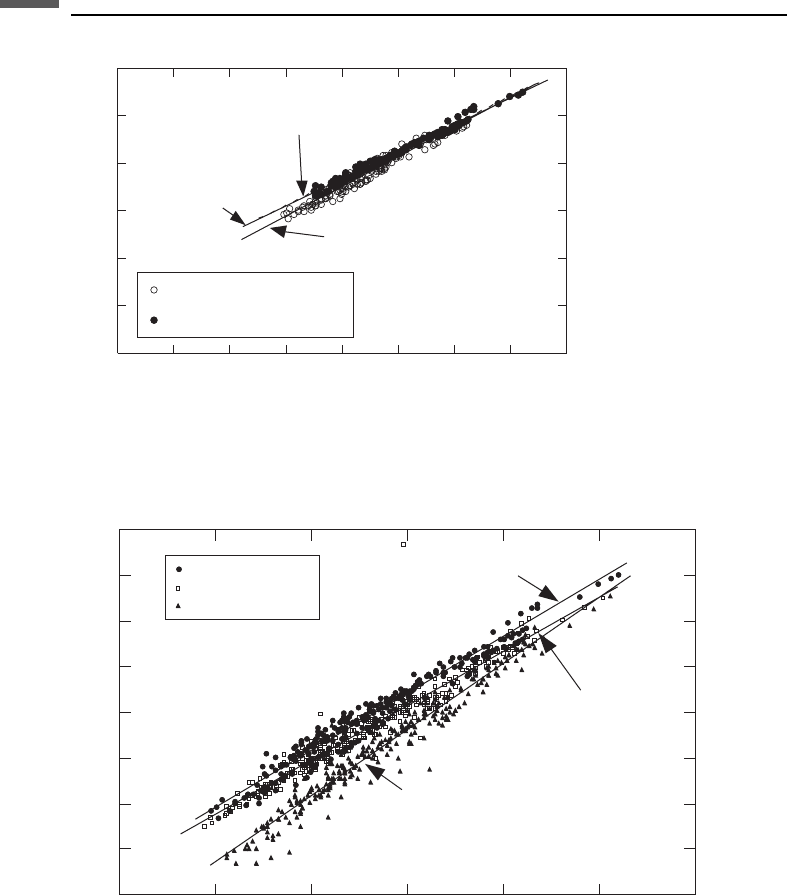
Note that the low-porosity line is very close to the mudrock line, which as we saw

above, fits the high clay values, whereas the high-porosity line is similar to the clean

sand (low-clay) regression in Figure 7.9.6.

Sandstones: effects of fluids and frequency

Figure 7.9.8 compares V

–V

at several conditions based on the shaley sandstone data

of Han (1986). The “dry” and “saturated ultrasonic” points are the measured ultrasonic

1234

Dry

Saturated high-f

Saturated low-f

(km/s)

Dry

Saturated

low-frequency

Saturated

ultrasonic

(Data from Han, 1986)

Figure 7.9.8 V

–V

for shaley sandstone under several different conditions described in the text.

01234

Water-saturated shaley sandstones

P-sat

for porosity > 15%

P-sat

for porosity < 15%

(km/s)

Porosity > 15%

= 0.7563V

− 0.6620

Porosity < 15%

= 0.8533V

−1.1374

Mudrock

= 0.8621V

− 1.1724

(Data from Han, 1986)

Figure 7.9.7 Laboratory ultrasonic V

–V

data for water-saturated shaley sands, differentiated

by porosity.

368 Empirical relations

data. The “saturated low-frequency” points are estimates of low-frequency saturated

data computed from the dry measurements using the low-frequency Gassmann’s

relations (see Section 6.3). It is no surprise that the water-saturated samples have

higher V

because of the well-known larger effects of pore fluids on P-velocities

than on S-velocities. Less often recognized is that the velocity dispersion that almost

always occurs in ultrasonic measurements appears to increase V

systematically.

Coal

Figure 7.9.9 shows laboratory ultrasonic data for coal (anthracite, semianthracite,

bituminous, cannel, and bituminous powder), measured by Marcote–Rios (personal

communication, 2007), plus data reported by Greenhalgh and Emerson (1986), Yu

et al. (1993), and Castagna et al. (1993) on bituminous coals. The Marcote–Rios

regression

¼ 0:4811V

þ 0:00382 ðkm=sÞ

is for all data in the plot. In addition, a quadratic fit is shown for the data published by

Greenhalgh and Emerson ( 1986) and Castagna et al. (1993), given by

¼0:232V

þ 1:5421V

 1:214 ðkm=sÞ

Critical porosity model

The P- and S-velocities of rocks (as well as their V

ratio) generally trend between

the velocities of the mineral grains in the limit of low porosity and the values for a

0 0.5 1 1.5 2 2.5 3 3.5

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

(km/s)

Anthracite

Semianthracite

Bituminous

Cannel

Bitum-powder

Other authors

Castagna et al.

Marcote – Rios

Figure 7.9.9 V

versus V

for different coals. The solid line is the best fit through all data.

The dashed line is for some bituminous coals.

369 7.9 V

–V

relations

mineral–pore-fluid suspension in the limit of high porosity. For most porous materials

there is a critical porosity, f

, that separates their mechanical and acoustic behavior

into two distinct domains. For porosities lower than f

the mineral grains are load-

bearing, whereas for porosities greater than f

the rock simply “falls apart” and

becomes a suspension in which the fluid phase is load-bearing (see Section 7.1 on

critical porosity). The transition from solid to suspension is implicit in the Raymer

et al. (1980) empirical velocity–porosity relation (see Section 7.4) and the work of

Krief et al. (1990), which is discussed below.

A geometric interpretation of the mineral-to-critical-porosity trend is simply that if

we make the porosity large enough, the grains must lose contact and their rigidity.

The geologic interpretation is that, at least for clastics, the weak suspension state at

critical porosity, f

, describes the sediment when it is first deposited before compac-

tion and diagenesis. The value of f

is determined by the grain sorting and angularity

at deposition. Subsequent compaction and diagenesis move the sample along an

upward trajectory as the porosity is reduced and the elastic stiffness is increased.

The value of f

depends on the rock type. For example f

 0.4 for sandstones;

 0.7 for chalks; f

 0.9 for pumice and porous glass; and f

 0.02–0.03 for

granites.

In the suspension domain, the effective bulk and shear moduli of the rock K and m

can be estimated quite accurately by using the Reuss (isostress) average (see Section

4.2 on the Voigt–Reuss average and Section 7.1 on critical porosity) as follows:



1  

;¼ 0

where K

and K

are the bulk moduli of the fluid and mineral and f is the porosity.

In the load-bearing domain, f < f

, the moduli decrease rapidly from the mineral

values at zero porosity to the suspension values at the critical porosity. Nur et al.

(1995) found that this dependence can often be approximated with a straight line

when expressed as modulus versus porosity. Although there is nothing special about a

linear trend of modulus versus f, it does describe sandstones fairly well, and it leads

to convenient mathematical properties. For dry rocks, the bulk and shear moduli can

be expressed as the linear functions

dry

¼ K

1 







dry

¼ 

1 





where K

and m

are the mineral bulk and shear moduli, respectively. Thus, the dry-

rock bulk and shear moduli trend linearly between K

, m

at f ¼0, and K

dry

¼m

dry

¼0

370 Empirical relations

at f ¼ f

. At low frequency, changes of pore fluids have little or no effect on the

shear modulus. However, it can be shown (see Section 6.3 on Gassmann) that with

a change of pore fluids the straight line in the K–f plane remains a straight line,

trending between K

at f ¼ 0 and the Reuss average bulk modulus at f ¼ f

Thus, the effect of pore fluids on K or V

¼ K þ

 is automatically incorporated

by the change of the Reuss average at f ¼ f

The relevance of the critical porosity model to V

–V

relations is simply that V

should generally trend toward the value for the solid mineral material in the limit

of low porosity and toward the value for a fluid suspension as the porosity

approaches f

(Castagna et al., 1993). Furthermore, if the modulus–porosity rela-

tions are linear (or nearly so), then it follows that V

for a dry rock at any

porosity (0 < f < f

) will equal the V

of the mineral. The same is true if K

dry

and m

dry

are any other functions of porosity but are proportional to each other

dry

(f) / m

dry

(f)]. Equivalently, the Poisson ratio v for the dry rock will equal

the Poisson ratio of the mineral grains, as is often observed (Pickett, 1963; Krief

et al., 1990).



dry rock





mineral

dry rock

 v

mineral

Figure 7.9.10 illustrates the approximately constant dry-rock Poisson ratio observed

for a large set of ultrasonic sandstone velocities (from Han, 1986) over a large range of

effective pressures (5 < P

eff

< 40 MPa) and clay contents (0 < C < 55% by volume).

0 5 10 15 20 25 30 35

Clay < 10%

Clay > 10%

dry

ν = 0.01

ν = 0.1

ν = 0.2

ν = 0.3

ν = 0.4

Shaley sandstones–dry

Figure 7.9.10 Velocity data from Han (1986) illustrating that Poisson’s ratio is approximately

constant for dry sandstones.

371 7.9 V

–V

relations

To summarize, the critical porosity model suggests that P- and S-wave velocities

trend systematically between their mineral values at zero porosity to fluid-suspension

values (V

¼ 0, V

¼ V

suspension

 V

fluid

) at the critical porosity f

, which is a

characteristic of each class of rocks. Expressed in the modulus versus porosity

domain, if dry rock rV

versus f is proportional to rV

versus f (for example, both

and rV

are linear in f), then V

of the dry rock will be equal to V

of the

mineral.

The V

–V

relation for different pore fluids is found using Gassmann’s relation,

which is applied automatically if the trend terminates on the Reuss average at f

(see

a discussion of this in Section 6.3 on Gassmann’s relation).

Krief’s relations

Krief et al. (1990) suggested a V

–V

prediction technique that very much resembles

the critical porosity model. The model again combines the same two elements.

1. An empirical V

–V

–f relation for water-saturated rocks, which we will show is

approximately the same as that predicted by the simple critical porosity model.

2. Gassmann’s relation to extend the empirical relation to other pore fluids.

If we model the dry rock as a porous elastic solid, then with great generality we

can write the dry-rock bulk modulus as

dry

¼ K

ð1  b Þ

where K

dry

and K

are the bulk moduli of the dry rock and mineral and b is Biot’s

coefficient (see Section 4.6 on compressibilities and Section 2.9 on the deformation

of cavities). An equivalent expression is

dry



where K

is the pore-space stiffness (see Section 2.9) and f is the porosity, so that





d

d



¼constant

; b ¼

d



¼constant

K

dry



where 

is the pore volume, V is the bulk volume, s is confining pressure, and P

pore pressure. The parameters b and K

are two equivalent descriptions of the pore-

space stiffness. Ascertaining b versus f or K

versus f determines the rock bulk

modulus K

dry

versus f.

Krief et al. (1990) used the data of Raymer et al. (1980) to find a relation for b

versus f empirically as follows:

ð1  bÞ¼ð1  Þ

mðÞ

; where mðÞ¼3=ð1  Þ

372 Empirical relations

Next, they used the empirical result shown by Pickett (1963) and others that the

dry-rock Poisson ratio is often approximately equal to the mineral Poisson ratio, or

dry

¼ m

. Combining these two empirical results gives

dry

¼ K

ð1  Þ

mðÞ



dry

¼ 

ð1  Þ

mðÞ

; where mðÞ¼3=ð1  Þ

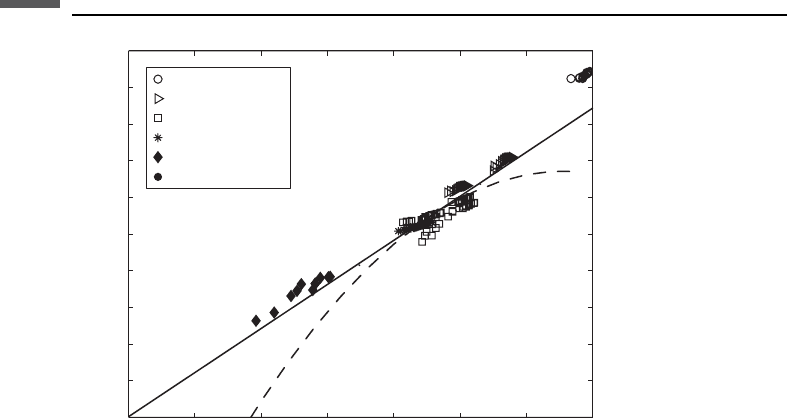
Plots of K

dry

versus f, m

dry

versus f, and b versus f are shown in Figure 7.9.11.

It is clear from these plots that the effective moduli K

dry

and m

dry

display the critical

porosity behavior, for they approach zero at f  0.4–0.5 (see the previous discus-

sion). This is no surprise because b(f) is an empirical fit to shaley sand data, which

always exhibit this behavior.

Compare these with the linear moduli–porosity relations for dry rocks suggested by

Nur et al. (1995) for the critical porosity model

dry

¼ K

1 







dry

¼ 

1 





0    

where K

and m

are the mineral moduli and f

is the critical porosity. These imply a

Biot coefficient of

b ¼

=

; 0    

1;>



0.2

0.4

0.6

0.8

0 0.2 0.4 0.6 0.8 1

Porosity

Critical-porosity model

Krief model

0.2

0.4

0.6

0.8

0 0.2 0.4 0.6 0.8 1

Biot coefficient

Porosity

Critical-porosity model

Krief model

Modulus (normalized)

Figure 7.9.11 Left: bulk and shear moduli (same curves when normalized by their mineral

values) as predicted by Krief’s model and a linear critical porosity model. Right: Biot coefficient

predicted by both models.

373 7.9 V

–V

relations

As shown in Figure 7.9.11, these linear forms of K

dry

, m

dry

, and b are essentially the

same as Krief’s expressions in the range 0  f  f

The Reuss average values for the moduli of a suspension, K

dry

¼ m

dry

¼ 0; b ¼ 1

are essentially the same as Krief’s expressions for f > f

. Krief’s nonlinear form

results from trying to fit a single function b(f) to the two mechanically distinct

domains, f < f

and f > f

. The critical porosity model expresses the result with

simpler piecewise functions.

Expressions for any other pore fluid are obtained by combining the expression

dry

¼ K

(1 – b) of Krief et al. with Gassmann’s equations. Although these are also

nonlinear, Krief et al. suggest a simple approximation

sat

 V

sat

 V

where V

P-sat

, V

, and V

are the P-wave velocities of the saturated rock, the mineral,

and the pore fluid, respectively, and V

S-sat

and V

are the S-wave velocities in the

saturated rock and mineral. Rewriting this slightly gives

sat

¼ V

þ V

sat

 V



which is a straight line (in velocity-squared) connecting the mineral point (V

, V

)

and the fluid point (V

, 0). We suggest that a more accurate (and nearly identical)

model is to recognize that velocities tend toward those of a suspension at high

porosity rather than toward a fluid, which yields the modified form

sat

 V

sat

 V

where V

is the velocity of a suspension of minerals in a fluid given by the Reuss

average (Section 4.2) or Wood’s relation (Section 4.3) at the critical porosity.

It is easy to show that this modified form of Krief’s expression is exactly equiva-

lent to the linear (modified Voigt) K versus f and m versus f relations in the critical

porosity model with the fluid effects given by Gassmann.

Greenberg and Castagna’s relations

Greenberg and Castagna (1992) have given empirical relations for estimating V

from

in multimineralic, brine-saturated rocks based on empirical, polynomial V

–V

relations in pure monomineralic lithologies (Castagna et al., 1993). The shear-wave

velocity in brine-saturated composite lithologies is approximated by a simple average

of the arithmetic and harmonic means of the constituent pure lithology shear

velocities:

374 Empirical relations

i¼1

j¼0

i¼1

j¼0

1

;

i¼1

¼ 1

where L is the number of pure monomineralic lithologic constituents, X

are the

volume fractions of lithological constituents, a

are the empirical regression coeffi-

cients, N

is the order of polynomial for constituent i, and V

and V

are the P- and

S-wave velocities (km/s), respectively, in composite brine-saturated, multimineralic

rock.

Castagna et al. (1993) gave representative polynomial regression coefficients for

pure monomineralic lithologies as detailed in Table 7.9.1. Note that the preceding

relation is for 100% brine-saturated rocks. To estimate V

from measured V

for other

fluid saturations, Gassmann’s equation has to be used in an iterative manner. In the

following, the subscript b denotes velocities at 100% brine saturation, and the

subscript f denotes velocities at any other fluid saturation (e.g., oil or a mixture of

oil, brine, and gas). The method consists of iteratively finding a (V

, V

) point on the

brine relation that transforms, with Gassmann’s relation, to the measured V

and

the unknown V

for the new fluid saturation. The resulting curves are shown in

Figure 7.9.12. The steps are as follows.

1. Start with an initial guess for V

2. Calculate V

corresponding to V

from the empirical regression.

3. Perform fluid substitution using V

and V

in the Gassmann equation to obtain V

4. With the calculated V

and the measured V

, use the Gassmann relation to obtain

a new estimate of V

. Check the result against the previous value of V

for

convergence. If convergence criterion is met, stop; if not, go back to step 2 and

continue.

When the measured P-velocity and desired S-velocity are for 100% brine satur-

ation, then of course iterations are not required. The desired V

is obtained from a

single application of the empirical regression. This method requires prior knowledge

Table 7.9.1 Regression coefficients for pure lithologies.

Lithology a

Sandstone 0 0.804 16 –0.855 88 0.983 52

Limestone –0.055 08 1.016 77 –1.030 49 0.990 96

Dolomite 0 0.583 21 –0.077 75 0.874 44

Shale 0 0.769 69 –0.867 35 0.979 39

Note:

and V

in km/s: V

¼ a

þ a

(Castagna et al., 1993).

375 7.9 V

–V

relations

of the lithology, porosity, saturation, and elastic moduli and densities of the constitu-

ent minerals and pore fluids.

Estimate, using the Greenberg–Castagna empirical relations, the shear-wave vel-

ocity in a brine-saturated shaley sandstone (60% sandstone, 40% shale) with V

3.0 km/s.

Here L ¼ 2 with X

(sandstone) ¼ 0.6 and X

(shale) ¼ 0.4.

The regressions for pure lithologic constituents give us

sand

¼ 0:804 16 V

 0:855 88 ¼ 1:5566 km=s

shale

¼ 0:769 69 V

 0:867 35 ¼ 1:4417 km=s

The weighted arithmetic and harmonic means are

arith

¼ 0:6V

sand

þ 0:4V

shale

¼ 1:5106 km=s

harm

¼ð0:6=V

sand

þ 0:4=V

shale

1

¼ 1:5085 km=s

and finally the estimated V

is given by

ðV

arith

þ V

harm

Þ¼1:51 km=s

Vernik’s relations

The Greenberg–Castagna (1992) empirical relations discussed previously are appro-

priate for consolidated rocks with P-wave velocities greater than about 2.6 km/s.

However, when extrapolated to low velocities, these relations yield unphysical

012345

(km/s)

Sandstone

Limestone

Dolomite

Shale

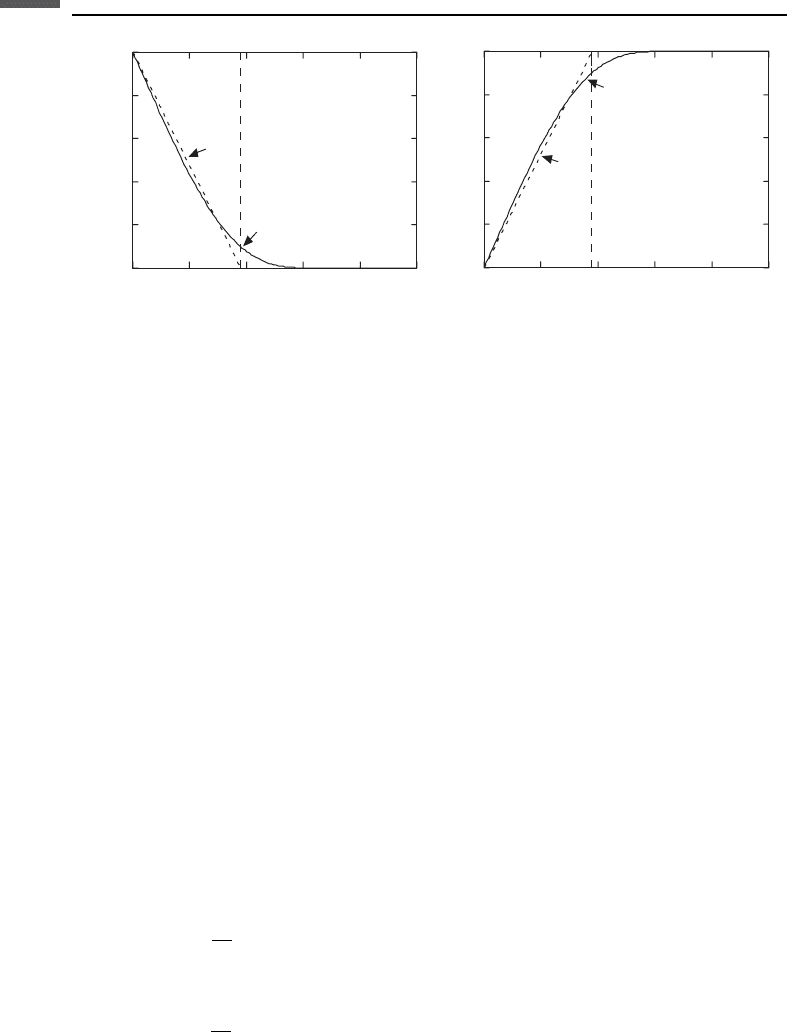
Figure 7.9.12 Typical V

–V

curves corresponding to the regression coefficients in Table 7.9.1.

376 Empirical relations