Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.

22-4
REFERENCE
DATA
FOR ENGINEERS
different messages can be transmitted. If
M
=
2k,
this
corresponds to a binary word of
k
bits. This modulation
technique is a form of block coding. In general, the
optimum detection strategy can be quite complicated.
However, when the optical detector
is
shot-noise limit-
ed, the maximum-likelihood receiver reduces to a
particularly simple form. For each time slot, the receiv-
er counts the number of detected photons in each of the
M
intervals. The transmitted message is assumed to be
the message corresponding to the interval with the
largest count. The probability of word error (PWE) for
this case is*
where,
a
a
=
(Nt/k!)/ Nib/i!
i=O
-
*
Reference
3.
I
I
In these expressions, N, is the expected signal photo-
count;
Nb
is the expected background noise count per
pulse interval; and
J,
and
Jb
are, respectively, the signal
and background noise energies per pulse interval. In
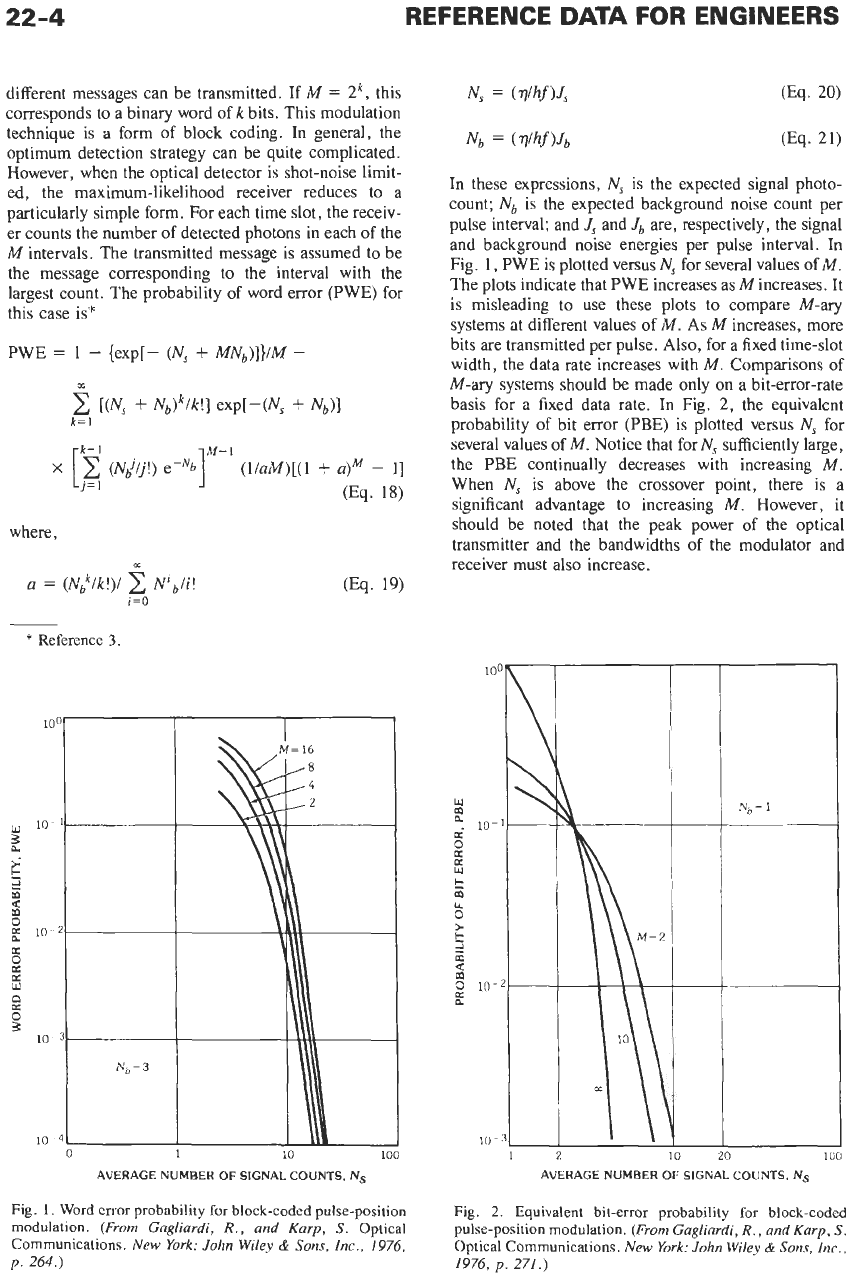
Fig.
1,
PWE is plotted versus N, for several values of
M.
The plots indicate that PWE increases as
M
increases. It
is misleading
to
use these plots to compare M-ary
systems at different values of
M.
As
M
increases, more
bits are transmitted per pulse. Also, for a fixed time-slot
width, the data rate increases with
M.
Comparisons of
M-ary
systems should be made only on a bit-error-rate
basis for a fixed data rate. In Fig.
2,
the equivalent
probability
of
bit error (PBE) is plotted versus N, for
several values of
M.
Notice that for N, sufficiently large,
the PBE continually decreases with increasing
M.
When N, is above the crossover point, there
is
a
significant advantage to increasing
M.
However, it
should be noted that the peak power of the optical
transmitter and the bandwidths of the modulator and
receiver must also increase.
looK
10-1
0
K
0
1
10
100
1
I
Nb=
1
t
L
20
AVERAGE NUMBER
OF
SIGNAL COUNTS,
Ns
AVERAGE NUMBER
OF
SIGNAL COUNTS,
Ns
Fig.
1.
Word
error
probability
for
block-coded pulse-position
modulation.
(From Gagliardi,
R.,
and
Kurp,
S.
Optical
Communications.
New
York:
John
Wiley
d;
Sons,
Inc.,
1976,
p.
264.)
Fig.
2.
Equivalent bit-error probability
for
block-coded
pulse-position modulation.
(From Gagliardi,
R.,
and
Karp,
S.
Optical Communications.
New
York:
John
Wiley
&
Sons,
Inc.,
1976,
p.
271
.)
OPTICAL COMMUNICATIONS
22-5
Binary Orthogonal Signaling
When
M
=
2,
we have binary modulation.
In
this
case, the PBE is given by*
PBE
=
i
(1
f
Q[m,
v2(Ns
+
Nb)]
-
Q[~~(Ns
f
Nb),
(Eq.
22)
where,
is Marcum’s
Q
function. This expression for the PBE is
also valid for other types of binary orthogonal signaling
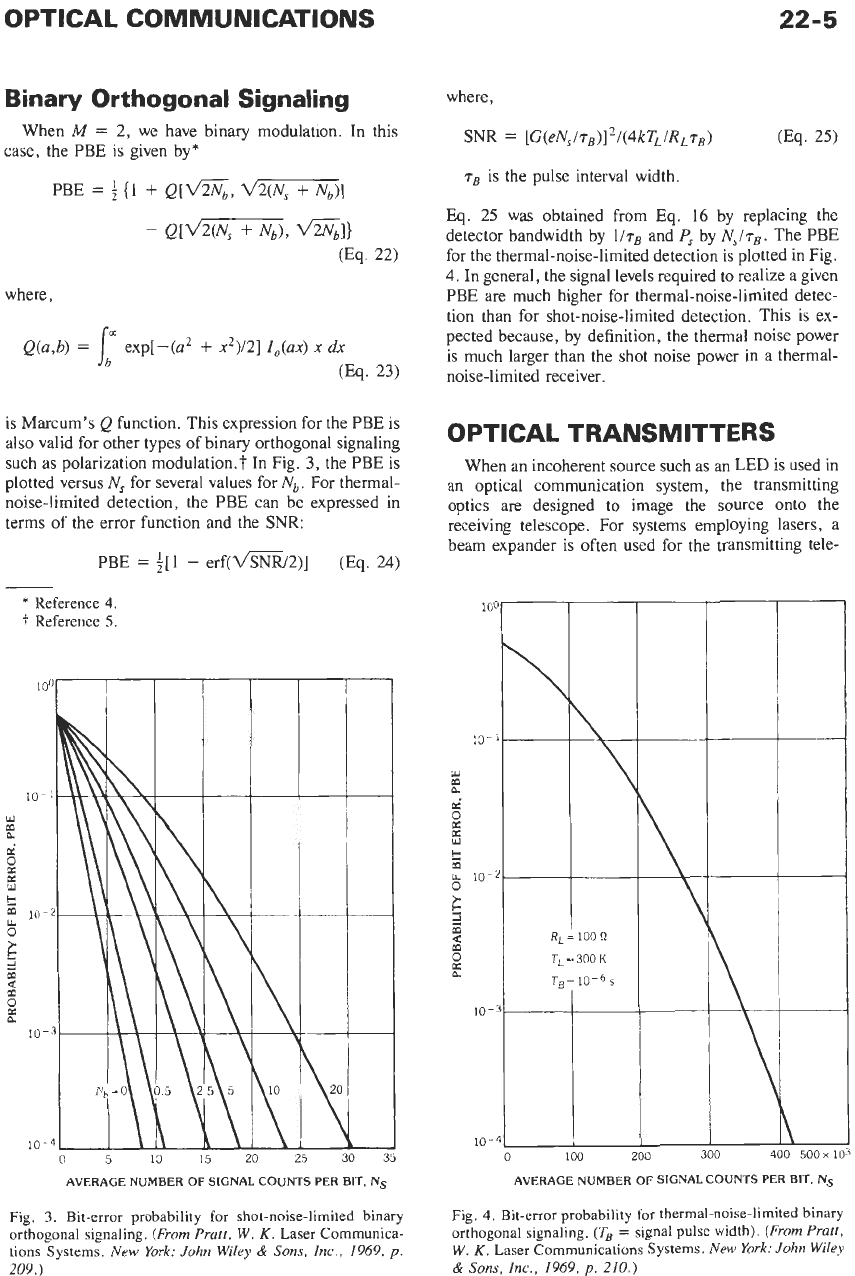
such as polarization modu1ation.t In Fig.
3,
the PBE is
plotted versus
N,
for several values for
Nb.
For thermal-
noise-limited detection, the PBE can be expressed in
terms
of
the error function and the
SNR:
PBE
=
i[l
-
erf(V%&2)]
(Eq.
24)
Reference
4.
?
Reference
5.
AVERAGE NUMBER
OF
SIGNAL
COUNTS
PER
BIT,
NS
Fig.
3.
Bit-error probability for shot-noise-limited binary
orthogonal signaling.
(From Pratt,
W.
K.
Laser Cornrnunica-
tions Systems.
New
York:
John
Wiley
&
Sons,
Inc.,
1969,
p.
209.)
where,
SNR
=
[G(~NJT,)]~/(~~T~
/R,
rB)
(Eq.
25)
78
is the pulse interval width.
Eq.
25
was
obtained from Eq.
16
by replacing the
detector bandwidth by
UT,
and
P,
by
Ns/rB.
The PBE
for the thermal-noise-limited detection is plotted
in
Fig,
4.
In
general, the signal levels required to realize a given
PBE are much higher for thermal-noise-limited detec-
tion than for shot-noise-limited detection. This is ex-
pected because, by definition, the thermal noise power
is much larger than the shot noise power in a thermal-
noise-limited receiver.
OPTICAL TRANSMITTERS
When an incoherent source such as an LED is used in
an optical communication system, the transmitting
optics are designed to image the source onto the
receiving telescope. For systems employing lasers, a
beam expander is often used for the transmitting tele-
10-4
0
100
200
300
400
500x
1(
AVERAGE NUMBER
OF
SIGNAL COUNTS PER BIT,
Ns
Fig.
4.
Bit-error probability
for
thermal-noise-limited binary
orthogonal signaling.
(TB
=
signal
pulse
width).
(From Pratt,
W.
K.
Laser Communications Systems.
New
York:
John
WiLey
&
Sons,
Inc.,
1969,
p.
210.)

22-6
REFERENCE
DATA
FOR ENGINEERS
scope to decrease beam divergence. The transmitter and
receiver can share the same telescope to reduce cost and
weight.
A
variety of telescope configurations have been
used in optical communication systems.
The most
common are the Cassegrain reflector and the simple
refracting telescope. Because of the high cost of low-
loss lens materials, reflecting optics are utilized almost
exclusively in systems operating at the middle and far
IR
wavelengths, Both reflecting and refracting telescopes
are used for near
IR
and visible systems.
Incoherent Sources
A
simple imaging telescope for an LED source is
diagrammed in Fig.
5.
The objective lens is designed to
project an image
of
the LED onto the receiver. The
image intensity depends on the image magnification and
the power radiated by the LED. The image magnifica-
tion
(m)
is the ratio of the image distance
(z)
to the
object distance
(Z,)
m
=
zIZ,
0%. 26)
The image and object distances are related through the
lens-maker’s equation
lif,
=
l/z
+
lIZ,
(Eq. 27)
wherefL is the lens focal length. By solving Eq. 27 for
the object distance, we obtain
z,
=
fLW
-
fL/4
0%. 28)
Usually, the image distance is large compared to the
lens focal length
so
that
2,
=
fL
and
m
=
zVL. The
image diameter
(d,)
is equal to the LED diameter
(dLED)
multiplied by the magnification
di
=
(?fL)dLED
(Eq. 29)
The total optical power in the image is equal to the
power collected by the transmitting telescope objective
multiplied by the atmospheric transmittance. To com-
pute the power collected by the objective, we need to
know the radiation pattern of the LED. If the LED has
no lens, the radiation is Lambertian and is proportional
tan-
11dL/2/L)
TELESCOPE
IMAGE
PLANE
OBJECTIVE
LED
Fig.
5.
Transmitting telescope
for
an
LED
source.
to the cosine
of
the angle between the observation point
and the optical axis. Many LEDs are packaged with
small lenses to collimate the radiation and reduce the
beamwidth. In most cases, the radiation pattern can be
fairly accurately modeled by the formula
PL(e,
4)
=
[(6
+
I)I~T]P,
COS^
e
(Eq. 30)
where,
6
=
-In 2lln cos (6,/2)
(Eq. 31)
0
and
4
are the spherical coordinate angles,
PL
is the total power emitted by the LED into the
eB
is the full-width at half-maximum (FWHM)
hemisphere,
beamwidth.
For a Lambertian source,
OB
=
120”
and
6
=
1.
For
LEDs,
OB
can be as small as 10” and
6
can approach
200.
The power collected by the objective lens is calculat-
ed by integrating the LED radiation pattern over the
solid angle of the lens.
=
PL[1
-
(1
+
dL2/4fL2)-(@1)’2]
(Eq. 32)
The quantity
PT
is the total power transmitted by the
telescope, and
dL
is the diameter of the telescope
objective lens. The maximum value of
PT
is
PL,
the total
power emitted by the LED. The bracketed term is a
factor describing the efficiency of the LED-telescope
combination. The efficiency increases with decreasing
beamwidth (increasing
8
and decreasing
fl
number
(fLldL)
of the objective lens. This is illustrated in Fig.
6,
where telescope efficiency is plotted versus the LED
LED
BEAMWIDTH
(FWHM)
Fig.
6.
Variation
of
the transmitting-telescope efficiency with
LED
beam width.

22-7
beamwidth for several values of the objective-lens
fl
number. For a Lambertian source, Eq. 32 reduces to
PT
=
PLd21(dL2
+
4L2)
(Eq.
33)
If we assume that the image is uniformly bright, then
the optical power density or signal intensity
(I,)
in the
receiver plane is equal to the total power in the image
divided by the image area. For a circular LED source,
the signal intensity is given by
I,
=
(4fL2/5Td2~~~)(GP~/Z2) (Eq. 34)
where
T,
is the atmospheric transmittance. As expected,
the signal intensity decreases inversely with the square
of the distance between the transmitter and receiver.
Although the telescope efficiency decreases with in-
creasing
&,
the
fL2
dependence in Eq. 34 dominates
so
that
I,
increases with increasing
fL.
However, this does
not always mean that it is better to have a large focal
length. The magnification and image size decrease with
increasing
fL
.
Smaller images require more precise
pointing and tracking. The maximum permitted point-
ing error
(8,)
is approximately equal to the arctangent
of the image radius divided by the image distance
8,
=
tan-’(di/2z)
=
tan-’(dLED/fL)
(Eq.
35)
This is the condition for the edge of the image to lie on
the optical axis of the receiving telescope. The transmit-
ting telescope must be pointed with an accuracy less
than the angle given by
Eq.
35. Small changes in the
pointing. angle can be obtained by moving the LED
perpendicular to the optical axis of the transmitting
telescope.
In direct analogy with conventions established in
microwave-communication systems analysis, it is some-
times convenient to express the signal power density in
terms of the transmitter or source power and an effective
antenna gain. In this case, Eq. 34 is written as
1,
=
(GT/4?I)(T,PL/z2) (Eq. 36)
where,
Coherent
Sources
For spatially coherent laser sources, the transmitting
telescope
is
usually a beam expander that is designed to
reduce the beam divergence. The spatial mode structure
of
laser resonators has been discussed extensively in the
literature.
*
The fundamental mode for a radially sym-
metric cavity has a Gaussian cross section
~~(x,y,z)
=
[~P~/T~~(z)I exp [-2(x2
+
y2)iw2(z)]
*
Reference
6.
(Eq. 38)
where,
I,
is the beam intensity,
PL
is the total power in the beam,
w(z) is the beamwidth at the
e-2
intensity point.
In
Eq.
38,
the optical axis of the laser is assumed to be
the
z
axis. The laser is located at the origin, and the
beam is propagating in the positive
z
direction. The
factor o(z) is a function of the beamwidth and phase-
front curvature at the laser. If the receiver is in the far
field, then w(z) can be written as
~(z)
=
z tan
eL
(Eq. 39)
where
8L
is the beam divergence angle. Usually,
8,
is a
few milliradians or less. The smallest beam is obtained
whenever the laser radiation is focused onto the receiver
plane. If the receiver is in the far field, this is equivalent
to collimating the beam. For a collimated beam, w(z) is
given by
w(z)
=
wo(l
+
A2z2/r2w2)’’2
(Eq. 40)
or
w(z)
=
wo[l
+
(Az/T~~)~]”~
where,
A
is the optical wavelength,
wo
is the beamwidth at the output of the beam
expander.
The divergence angle for a collimated beam is
8L
=
hiroo
(Eq. 41)
In the far field, the on-axis signal intensity is calculated
by substituting
Eq.
40 into
Eq.
38 and evaluating the
result at
x
=
y
=
0:
I,
=
(2rw21h2) (GPL/z2)
(Eq.
42)
where
To
is the atmospheric transmittance. This expres-
sion is similar to Eq. 34 for incoherent sources. The
beam divergence decreases and the on-axis intensity
increases with increasing beamwidth,
wo.
It is sometimes convenient to express the on-axis
intensity in terms of an equivalent antenna gain:
where,
GT
=
8r2W2/A2
(Eq.
44)
Because a Gaussian beam is infinite in extent, Eq. 44 is
the maximum gain that would be obtained with an
infinitely large beam expander. However, in practice,
the beam will be truncated by thle finite extent of the
transmitting aperture. In addition, if a Cassegrain
22-8
REFERENCE
DATA
FOR ENGINEERS
reflecting telescope is used to expand the beam, the
central obscuration caused by the secondary mirror will
also reduce the effective gain. It is necessary to match
the beamwidth to the telescope to minimize the gain
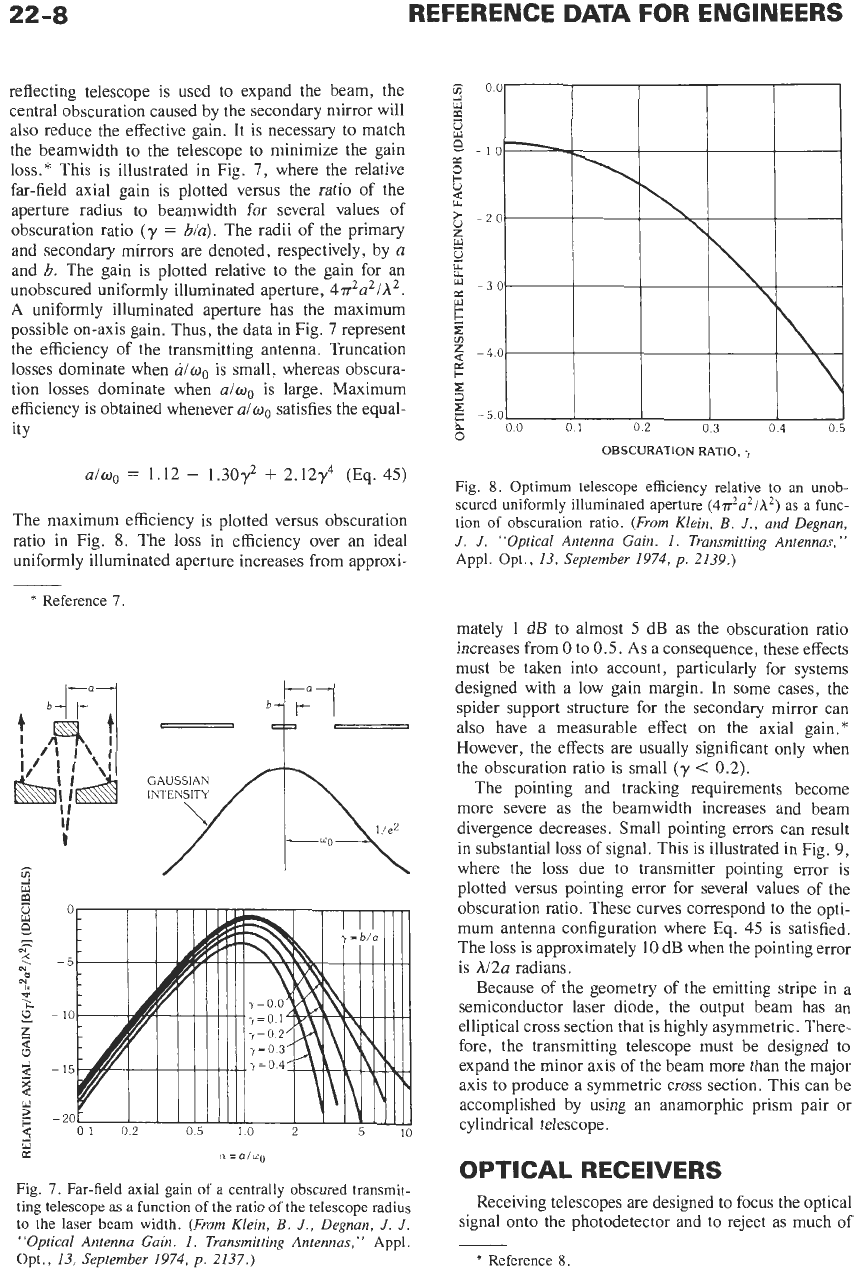
loss.* This is illustrated in Fig.
7,
where the relative
far-field axial gain is plotted versus the ratio of the
aperture radius to beamwidth for several values of
obscuration ratio
(y
=
bia).
The radii of the primary
and secondary mirrors are denoted, respectively, by
a
and
b.
The gain is plotted relative to the gain for an
unobscured uniformly illuminated aperture,
4.rr2a2/h2.
A
uniformly illuminated aperture has the maximum
possible on-axis gain. Thus, the data
in
Fig.
7
represent
the efficiency
of
the transmitting antenna. Truncation
losses dominate when
u/wo
is small, whereas obscura-
tion losses dominate when
a/wo
is large. Maximum
efficiency is obtained whenever
aimo
satisfies the equal-
ity
OBSCURATION RATIO.
Y
a/q
=
1.12
-
1.30~’
+
2.12~~ (Eq.
45)
The maximum efficiency is plotted versus obscuration
ratio in Fig.
8.
The loss in efficiency over an ideal
uniformly illuminated aperture increases from approxi-
Fig.
8.
Optimum telescope efficiency relative to
an
unob-
scured uniformly illuminated aperture
(47~*a~/h~)
as
a func-
tion
of
obscuration ratio.
(From Klein,
E.
J.,
and Degnan,
J.
J.
“Optical Antenna Gain.
1.
Transmitting Antennas,”
Appl. Opt.,
13, September 1974, p. 2139.)
*
Reference
7.
-
f
I-
m
0
u0
W
m-
1
-5
mi
:
-
$
-10
5
(3
2
-15
w
2
2
-20
4
01
02
05
10
2
5
10
Fig.
7.
Far-field axial gain of a centrally obscured transmit-
ting telescope as a function
of
the ratio
of
the telescope radius
to the laser beam width.
(From Klein,
E.
J.,
Degnan,
J.
J.
“Optical Antenna Gain.
I,
Transmitting Antennas,”
Appl.
Opt.,
13,
September 1974, p. 2137.)
mately
1
dB to almost
5
dB as the obscuration ratio
increases from
0
to
0.5.
As
a consequence, these effects
must be taken into account, particularly for systems
designed with a low gain margin. In some cases, the
spider support structure for the secondary mirror can
also have a measurable effect on the axial gain.*
However, the effects are usually significant only when
the obscuration ratio is small
(y
<
0.2).
The pointing and tracking requirements become
more severe as the beamwidth increases and beam
divergence decreases. Small pointing errors can result
in substantial loss of signal. This is illustrated in Fig.
9,
where the
loss
due to transmitter pointing error is
plotted versus pointing error for several values of the
obscuration ratio. These curves correspond to the opti-
mum antenna configuration where Eq.
45
is satisfied.
The loss is approximately
10
dB when the pointing error
is
h/2a radians.
Because
of
the geometry of the emitting stripe
in
a
semiconductor laser diode, the output beam has an
elliptical cross section that is highly asymmetric. There-
fore, the transmitting telescope must be designed
to
expand the minor axis
of
the beam more than the major
axis to produce a symmetric cross section. This can be
accomplished by using an anamorphic prism pair or
cylindrical telescope.
OPTICAL RECEIVERS
Receiving telescopes are designed to focus the optical
signal onto the photodetector and to reject as much
of
*
Reference
8.
22-9
FOCUSING
COLLlMATlNG
--*--
0
(XI20
RADIANS)
Fig.
9.
The decibel
loss
due to transmitter pointing error as
a
function of the angular pointing error for optimum antenna
configuration (maximum far-field gain) for several values
of
the obscuration ratio.
(From Klein,
B.
J.
and Degnan,
J. J.
“Optical Antenna Gain.
I.
Transmitting Antennas,”
Appl.
Opt.,
13,
September
1974,
p.
2139.)
the background radiation as is practical. Interference
filters are employed to eliminate background radiation
that is not the same wavelength as the optical signal.
Field stops are used to reject radiation that is not
emitted from the region surrounding the transmitting
telescope. Direct-detection receivers respond to the
signal intensity and are the most widely used in
communication systems. In heterodyne-detection re-
ceivers, the optical signal
is
combined with a local-
oscillator beam, and then both signals are focused onto
the same detector. Heterodyne-detection receivers re-
spond to signal amplitude and are used primarily in the
far infrared to overcome limitations imposed by poor
detector sensitivity.
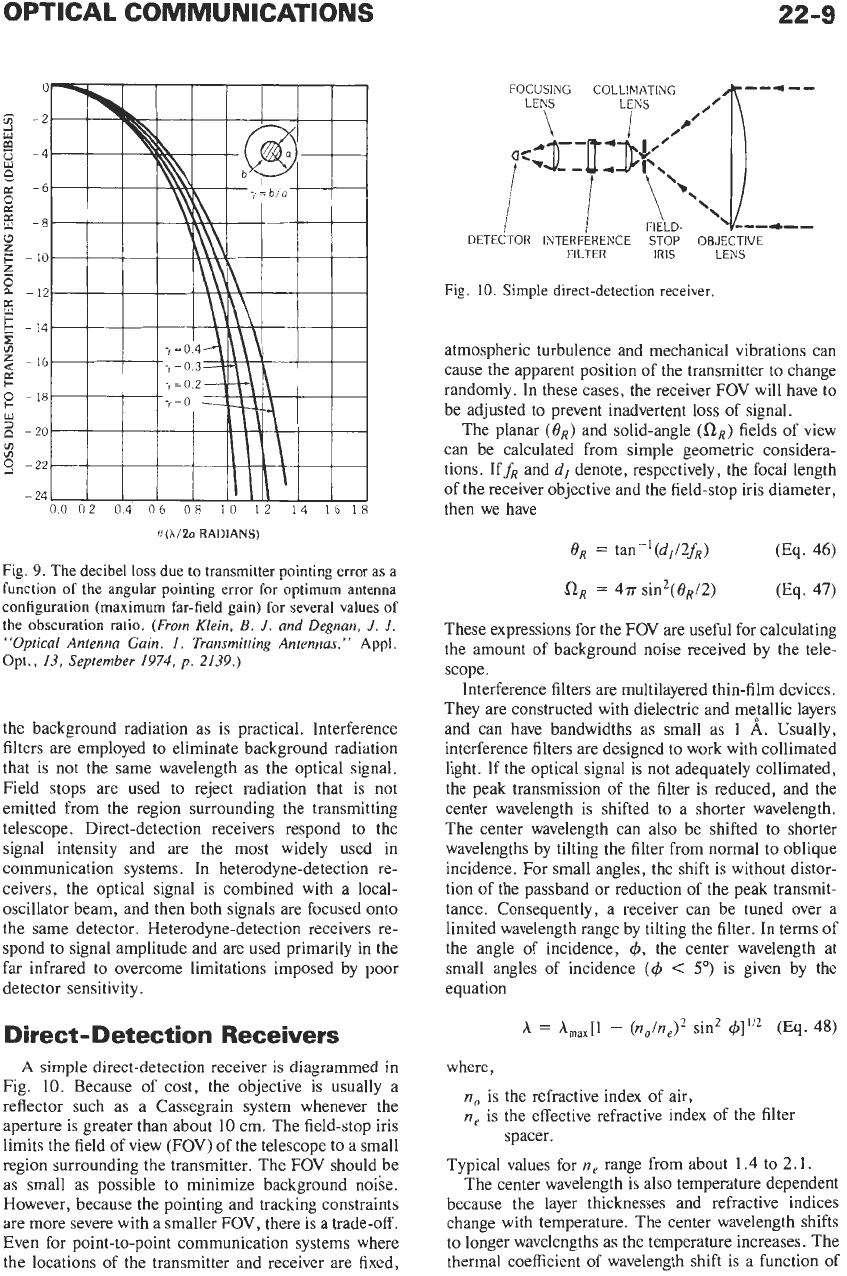
Direct-Detection Receivers
A
simple direct-detection receiver is diagrammed in
Fig.
10.
Because of cost, the objective is usually a
reflector such as a Cassegrain system whenever the
aperture is greater than about 10 cm. The field-stop iris
limits the field of view (FOV) of the telescope to a small
region surrounding the transmitter. The FOV should be
as small as possible to minimize background noise.
However, because the pointing and tracking constraints
are more severe with a smaller
FOV,
there is a trade-off.
Even for point-to-point communication systems where
the locations of the transmitter and receiver are fixed,
.-4--
OBJECTIVE
FILTER
IRIS
LENS
Fig.
IO.
Simple direct-detection receiver.
atmospheric turbulence and mechanical vibrations can
cause the apparent position of the transmitter to change
randomly. In these cases, the receiver
FOV
will have to
be adjusted
to
prevent inadvertent loss of signal.
The planar
(6,)
and solid-angle
(a,)
fields of view
can be calculated from simple geometric considera-
tions. Iff, and d, denote, respectively, the focal length
of the receiver objective and the field-stop iris diameter,
then we have
These expressions for the FOV are useful for calculating
the amount of background noise received by the tele-
scope.
Interference filters are multilayered thin-film devices.
They are constructed with dielectric and medallic layers
and can have bandwidths as small as
1
A.
Usually,
interference filters are designed to work with collimated
light. If the optical signal is not adequately collimated,
the peak transmission of the filter is reduced, and the
center wavelength is shifted to a shorter wavelength.
The center wavelength can also be shifted to shorter
wavelengths by tilting the filter from normal to oblique
incidence. For small angles, the shift is without distor-
tion of the passband or reduction of the peak transmit-
tance. Consequently, a receiver can be tuned over a
limited wavelength range by tilting the filter. In terms
of
the angle
of
incidence,
4,
the center wavelength at
small angles
of
incidence
(4
<
5”)
is given by the
equation
A
=
h,,,[l
-
(noin,)’
sin2
41’”
(Eq.
48)
where,
no
is the refractive index of air,
ne
is
the effective refractive index
of
the filter
Typical values for
ne
range from about
1.4
to
2.1.
The center wavelength is also temperature dependent
because the layer thicknesses and refractive indices
change with temperature. The center wavelength shifts
to longer wavelengths as the temperature increases. The
thermal coefficient
of
wavelength shift is a function of
spacer.

22-10
REFERENCE
DATA
FOR ENGINEERS
wavelength and filter construction. For visible and near
IR wavelengths, tte coefficient varies from approxi-
mately
0.1
to
0.3
A/”C.
To maintain proper tuning, it is
usually necessary to mount the filter in a teFperature-
controlled oven for bandwidths below
10
A
FWHM.
The peak transmittance
of
interference filters is a
decreasing function of the bandwidth. Typical values
r!nge from over
70%
for bandwidths on the order of
1tO
A
to less than
10%
for bandwidths on the order of 1
A.
The received signal power is calculated by multiply-
ing the signal power density times the receiver area
(AR)
and efficiency
(qR):
Ps
=
~/RAR(GT/~T)
(TaP~/Z2)
(Eq. 49)
where,
PL
is LED or laser power,
GT is the transmitting antenna gain,
T,
is the atmospheric transmittance.
Efficiency
qR
includes the effects of reflective and
absorptive losses in the receiver optics including the
interference filter. Low-loss optical materials and anti-
reflection coatings can reduce losses to a few percent or
less for each lens or mirror. Because losses are wave-
length dependent, the optics should be coated for the
specific wavelength
of
interest to obtain optimum per-
formance.
Equation 49 can be expressed in terms of an equiva-
lent receiving antenna gain
(GR):
where,
GR
=
4TA,/h2 (Eq.
51)
A
transmitting-antenna efficiency factor
(qT)
has been
included in Eq.
50
to account for losses in the transmit-
ter optics. The transmitting antenna gain is given by Eq.
37
for LED sources and by Eq. 44 for laser sources with
a Gaussian cross section. The factor (N47~z)’ is called
the free-space loss and represents the effect of path
length on the signal strength. The
SNR
for a direct-
detection receiver is calculated by substituting Eq.
50
into Eq. 15. The background noise power can be
computed
from
the data presented in the section on
background radiation.
Heterodyne- Detection
Receivers
A
simple heterodyne-detection receiver telescope is
diagrammed in Fig.
11.
The local oscillator
(LO)
beam
is combined with the optical signal, and both are
focused onto the same detector. Because the objective
and collimating lenses demagnify the signal beam, the
receiving telescope illustrated in Fig.
11
is optically
equivalent to combining the signal and LO in front of
DETECTOR COLLIMATING
,k-*
--
LENS
/I\
BEAM
SIGNAL
AMPLIFIER
OBJECTIVE
LENS
E,
n
LOCAL~O%LLATOR
BEAM
Fig.
11.
Simple heterodyne-detection receiver.
the objective lens. Optical mixing of the signal and LO
beams produces an intermediate-frequency (IF) signal
in the detector output that
is
proportional to the sig-
nal amplitude. The IF is the difference between the
signal and LO frequencies.
The electric field vectors for the signal
(E,)
and LO
(ELO)
can be written in the form
E,
=
As
cos(2-rrf,t
+
+s)
(Eq. 52)
0%.
53)
ELO
=
ALO
COG’T~LO~
+
+LO)
where,
A,
and
A,,
are the vector amplitudes,
f,
and
ho
are the optical frequencies,
+s
and
+Lo
are the phases of the signal and
LO,
The amplitudes and phases of both beams can depend
on time and position. The detector responds to the total
incident power, which is calculated by integrating over
the receiver aperture the magnitude squared of the total
field:
respectively.
pD
=
1
IEs
+
dxdy
=
P,
+
PLO
+
SIF
Receiver
Aperture
(Eq. 54)
The bar in Eq. 54 represents a time average over an
interval that is short compared to the inverse
of
the
detector bandwidth but is long compared to the optical
periods of the signal and LO. Terms
Ps
and
PLo
are,
respectively, the total signal and LO powers focused
onto the detector by the telescope. Term
S,F
is the
IF
signal, which is given by
Receiver
Aperture
where,

22-1
1
The receiver sensitivity and
SI^
are maximum when
the polarization, amplitude distribution, and phase of
the
LO
beam are matched to the signal beam.* If the
receiver is in the far field and the effects of atmospheric
turbulence are neglected, the signal beam can be
approximated as a uniform plane wave. Then for
uniform
LO
and signal beams,
As
and
A,,
are constant
throughout the receiver aperture and can be moved
outside the integral sign in Eq.
55.
To obtain maximum
sensitivity, the signal and LO beams must be properly
aligned. Small pointing errors can significantly reduce
the IF signal strength. To illustrate, the phase fronts of
the signal beam are assumed to be tilted with respect to
the
LO.
The
LO
phase is constant, and the signal phase
is
4s
=
$0
+
(2dA)y Sin
OR
(Eq.
57)
For simplicity, the coordinate system was chosen
so
that
the tilt
(0,)
is
with respect to the y-axis. Angle
OR
may
be regarded as the angular pointing error of the receiver.
After substituting Eq.
57
into Eq.
55
and carrying out
the integration for an unobscured circular aperture, we
obtain
2JI[(2.rra/A)
sin
OR]
(27ra/A) sin
OR
AS
'
SIF
=
cos(2~IFt
+
40
-
$LO)
(Eq.
58)
where,
A,
is the receiver aperture area
(Tu2),
a
is the aperture radius,
JI
is a Bessel function of the first RESET TO
ADD ONE LINEkind.
The factor involving the Bessel function is a gain-
reduction factor related to pointing error. When
@R
is zero (Le., perfect
LO
and signal beam alignment),
this factor is one. The
IF
signal is proportional to
the LO amplitude, By increasing the LO power, the
IF
signal can be made much larger than the receiver
thermal noise and the signal and background shot
noises. Typically, the limiting noise for heterodyne
detection is shot noise contributed by the
LO.
There is
an
IF
signal contribution due to background noise.
However, for typical IF filter bandwidths
(BIF
less than
approximately 1
GHz),
this background-noise contribu-
tion is small compared to the
IF
laser signal and can be
neglected.
The detector output is processed by an IF amplifier
and filter and final demodulator. The expected current
at the IF-amplifier output due to the optical signal is
calculated by substituting
Eq.
58
into Eq.
11
and is
*
Reference
3.
If the polarization of the
LO
is matched to the signal,
the IF signal power is given by
U,(27raiA)
sin
OR
(2.na/h) sin
OR
PlF
=
2(~eG/hf)~
(
)
PLOPS
where.
The noise power is calculated from Eq.
12
with
B
replaced by the IF bandwidth
(BiF)
and
PLo
added to the
signal and background shot-noise power. Therefore,
when the pointing error is zero, the IF SNR is given by
If the
LO
power is large, the thermal noise power and
the signal plus background shot-noise power will be
negligible compared to the
LO
shot-noise power. In this
case, the SNR reduces to
The signal power can be calculated from Eq.
50,
which
was derived for a direct-detection receiver. The back-
ground noise power can be computed from the data
presented in the section on background radiation.
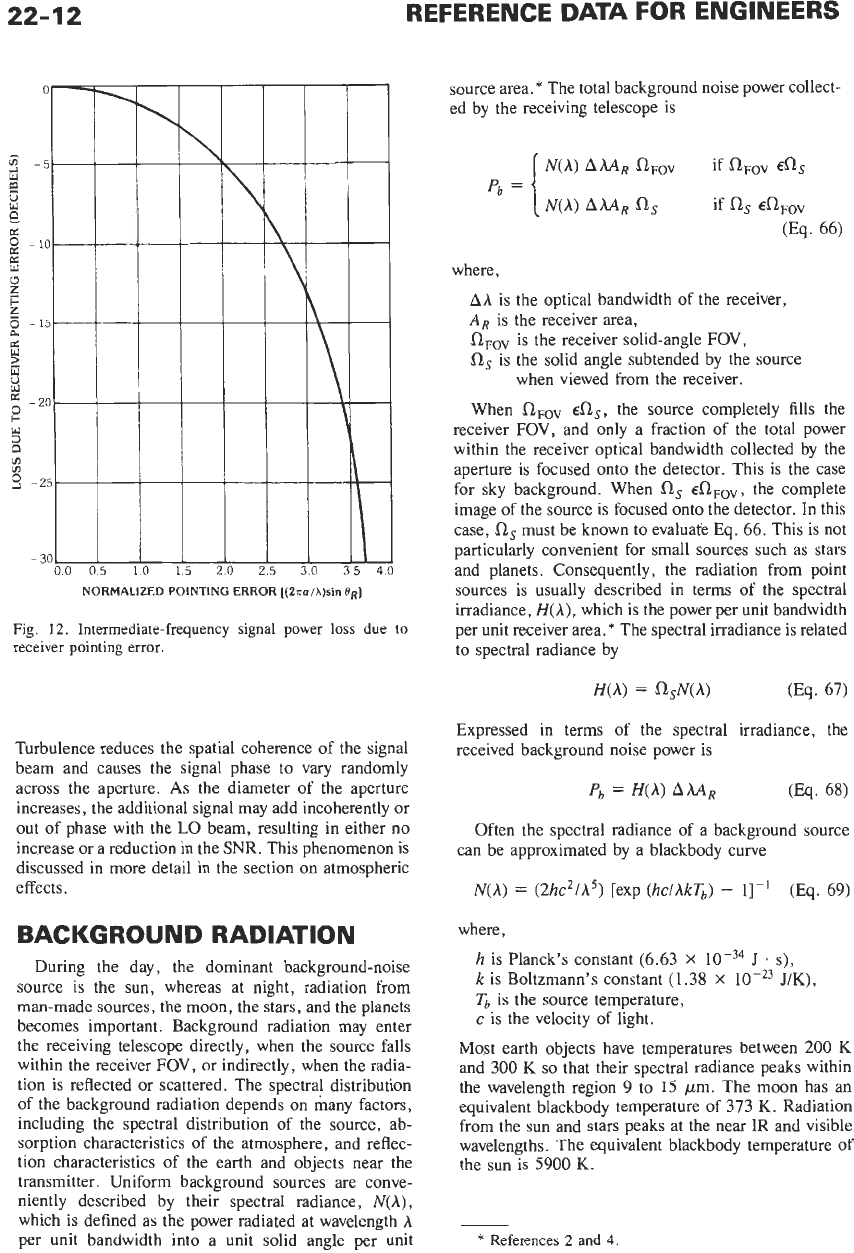
The pointing error can have a significant effect on the
IF SNR. This is illustrated in
Fig.
12,
where the
IF
SNR
loss
in decibels is plotted versus normalized pointing
error for an unobscured circular aperture and uniform
LO beam. To prevent significant
loss,
the pointing error
must be very small. The condition for negligible
loss
is
Equation
65
is the condition for pointing within the
diffraction-limited FOV
of
the telescope. Signals that
lie outside the diffraction-limited
FOV
will be rejected
by the telescope. Consequently, the pointing and track-
ing requirements for heterodyne-detection receivers are
quite severe.
In practice, atmospheric turbulence will cause the
amplitude and phase of the signal beam to fluctuate
randomly in space and time. The effect reduces the IF
signal power, particularly when the receiving aperture is
large. The
IF
signal strength is maximum when the
LO
and signal beams add coherently across the aperture.
22-12
REFERENCE
DATA
FOR ENGINEERS
NORMALIZED POINTING ERROR
[(ZaolX)sin
OR]
Fig.
12.
Intermediate-frequency signal power
loss
due to
receiver pointing
error.
Turbulence reduces the spatial coherence of the signal
beam and causes the signal phase to vary randomly
across the aperture.
As
the diameter of the aperture
increases, the additional signal may add incoherently or
out of phase with the
LO
beam, resulting in either no
increase or a reduction in the SNR. This phenomenon is
discussed in more detail in the section on atmospheric
effects.
BACKGROUND RADIATION
During the day, the dominant background-noise
source is the sun, whereas at night, radiation
from
man-made sources, the moon, the stars, and the planets
becomes important. Background radiation may enter
the receiving telescope directly, when the source falls
within the receiver FOV, or indirectly, when the radia-
tion is reflected or scattered. The spectral distribution
of the background radiation depends on many factors,
including the spectral distribution of the source, ab-
sorption characteristics of the atmosphere, and reflec-
tion characteristics of the earth and objects near the
transmitter. Uniform background sources are conve-
niently described by their spectral radiance,
N(A),
which is defined as the power radiated at wavelength
A
per unit bandwidth into a unit solid angle per unit
source area.
*
The total background noise power collect-
ed by the receiving telescope is
N(A)
AAAR
RFOV
if
N(A)
A~R
as
if
0s
E&OV
(Eq. 66)
where,
Ah
is the optical bandwidth of the receiver,
A,
is the receiver area,
aFov
is the receiver solid-angle FOV,
R,
is the solid angle subtended by the source
when viewed from the receiver.
When
RFov
€as,
the source completely fills the
receiver FOV, and only a fraction of the total power
within the receiver optical bandwidth collected by the
aperture is focused onto the detector. This is the case
for sky background. When
R,
eRFoV,
the complete
image of the source is focused onto the detector. In this
case,
a,
must be known to evaluate Eq. 66. This is not
particularly convenient for small sources such as stars
and planets. Consequently, the radiation from point
sources is usually described in terms of the spectral
irradiance,
H(A),
which is the power per unit bandwidth
per unit receiver area.
*
The spectral irradiance is related
to spectral radiance by
H(A)
=
aSN(h)
(Eq. 67)
Expressed in terms
of
the spectral irradiance, the
received background noise power is
Pb
=
H(A)
AAAR
(Eq. 68)
Often the spectral radiance of a background source
can be approximated by a blackbody curve
N(A)
=
(2hc2/h5)
[exp
(hclAkT,)
-
11-'
(Eq. 69)
where,
h
is Planck's constant (6.63
X
k
is Boltzmann's constant (1.38
X
Tb
is the source temperature,
c
is the velocity of light.
J
*
s),
J/K),
Most earth objects have temperatures between
200
K
and 300
K
so
that their spectral radiance peaks within
the wavelength region
9
to
15
pm. The moon has an
equivalent blackbody temperature of 373
K.
Radiation
from the sun and stars peaks at the near IR and visible
wavelengths. The equivalent blackbody temperature of
the sun is
5900
K.
*
References
2
and
4

OPTICAL COMMUNICATIONS
22-13
Absorption in the atmosphere of the earth can
significantly alter the spectral radiance of a background
source. This is illustrated in Fig. 13, where the spectral
irradiance
of
the sun outside the atmosphere of the earth
and at sea level is plotted.
Also
noted in the figure are
the atmospheric constituents that are responsible for
some of the major absorption bands. Fig.
14
illustrates
the measured spectral radiance of the clear daytime sky.
(The zenith angle of the sun is
45”,
and the visibility is
excellent.) The radiance for sunlit clouds is approxi-
mately one order of magnitude larger. On a clear day,
the color temperature of the sky is approximately
20
000
K
to
25
000
K.
The spectral irradiances of planets and stars also
approximate blackbody radiation curves. Fig.
15
shows
the calculated spectral irradiances outside the atmos-
phere of the earth from the planets. It is likely that many
stars of widely differing temperatures will be within the
receiver FOV. The probable spectral irradiance from a
one-square-degree star field near the galactic plane is
plotted in Fig. 16.
If the background radiation is due to the reflection of
the sun and sky, knowledge of the reflectance of the
2501
2ooc
-
.-
I
E
5
I
E
k
150C
-
:
8
g
l0OC
w
s
a
a
c
u
Y
a
w
50(
r
I
I
I
I
I
I
I
\
0.4
(
terrain surrounding the transmitter is required. In Fig.
17,
the typical reflectances of water, snow, soil, and
vegetation are plotted versus wavelength.
ATMOSPHERIC
EFFECTS
Absorption, scattering, and turbulence affect any
optical signal that propagates through the atmosphere of
the earth. Absorption by minor constituents such as
water vapor, carbon dioxide, and ozone can significant-
ly attenuate the signal beam. Rayleigh scattering by air
molecules and Mie scattering by larger particles such as
aerosols, dust, and clouds also attenuate the signal.
Turbulence is caused by small temperature fluctuations
in the atmosphere that give rise to random variations in
the refractive index. The optical signal is scattered by
these refractive inhomogeneities. Portions of the signal
that are scattered by different inhomogeneities interfere
at the receiver aperture. The amplitude and phase of the
total signal vary randomly in space and time. This loss
of signal coherence results in reduced gain and fading in
both direct-detection and heterodyne-detection receiv-
ers.
cop
.--
-
WAVELENGTH
(pm)
Fig. 13.
Solar
spectral
irradiance
with
sun
at
zenith.
(From Gair,
P. R.
“Solar Spectral Irradiance,” in
Handbook
of
Geophysical
and
Space Environment,
See.
16.1,
S.
L.
Valley,
ed. Cambridge,
Mass.,
1965)
