Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


23-6
REFERENCE DATA FOR ENGINEERS
A,
cos
(w,t
+
0,)
I
Fig.
7.
Block diagram of double-sideband
(DSB)
receiver.
(From P. F. Punter,
Modulation, Noise, and Spectral Analy-
sis,
Fig.
6-1,
@
1965,
MeGraw-Hill
Book
Co.)
signal e,@), as shown in Fig.
7.
The detected output
after filtering is given by
e&)
=
kg(t) cos(+,
-
+o),
k
=
constant
where
(+c
-
+o)
represents the phase difference
between the transmitted carrier and the locally generat-
ed oscillator. When the local carrier is in phase with the
incoming carrier, the detected signal is maximum. The
output signal-to-noise ratio
(SIN),
is related to the input
signal-to-noise ratio
(SIN),
by the expression
where the noise in each case is measured in a band
occupied by the signal. This represents a maximum
improvement of
3
decibels when the local oscillator is in
phase with the incoming carrier.
AM Detection
Synchronous Detection:
where
<g>
*(t)
equals the mean-square value of the
message function, which is maximum for
m,
=
1
and
Envelope Detection: In case of a carrier much strong-
er than the noise (high input carrier-to-noise ratio), we
have
9,
=
40.
which is identical to the case of synchronous detection
with
+,
=
cp0.
In case of poor input carrier-to-noise ratio, the
message function
g(t)
may be lost in the noise, which
results in a threshold effect. This effect exists only in
envelope detection and does not exist if synchronous or
coherent detection is used.
SSB
Detection
(S/N),/(S/N),
=
cos2(+c
-
do)
where the signal component of the output is measured
by the correlation of the detected output with the
transmitted signal.
COMPARISON
OF
SYSTEMS
AMPLITUDE-MODULATION
For equal power in the sidebands, the output signal-
For the same average total transmitted power, the
to-noise power ratios are identical.
following relations hold.
(S/N),(DSB)/(S/N),(AM)
=
1
+
r-’
where
r
equals the ratio of the mean-square power of the
message function to its peak power, and
(SIN)
,
(DSB)/(S/N
)
,
(SSB
)
=
1
For equal peak power
(SIN)
,
(DSB)I(S/N
)
(AM)
=
4
for any waveform of the modulating signal.
To
compare the merits of
SSB
versus
DSB
and
AM
on the basis of the signal-to-noise ratio, the waveform of
the modulating signal must be specified. This is illus-
trated in Fig.
8
for a modulating signal sin”x,
0
5
v
5
1.
EXPONENTIAL MODULATION
In exponential or angular modulation, the carrier
analytic signal A,exp[j(o,t
+
+,)I
is multiplied by the
transformed message function exp[ jflt)] to produce an
angle-modulated carrier analytic signal.
=
Re{A,exP[j(%t
+
4,)l
.
exp[jflt)lI
where,
A,
=
amplitude
of
unmodulated carrier,
5-
SINE SQUARE
WAVE
2
WAVE
FORM FACTOR OF MODULATING SIGNAL,
Y
Fig.
8.
Average-to-peak power relations as a function
of
modulating signal.
(After
W.
K.
Squires
and
E.
Bedrosian,
‘
‘The Computation
of
Single-Sideband Peak Power,
”
Proceed-
ings
of
the
IRE,
Vol.
48,
p.
124,
Fig.
2;
January
1960.)

ANALOG COMMUNICATIONS
23-7
w,
=
angular frequency of unmodulated carrier,
4,
=
carrier phase angle,
40)
=
[act
+
4,
+
W)l,
=
instantaneous phase angle modulated by the
message function,
g(t).
Expanding Eq.
1
in powers of
I(lit),
we have
=
Re& exp[j(w,t
+
4AI
X
[1
+
jW
-
(1/2!)1,@(t)
-
j(l/3!)G3(t)
+
.
*
1)
When
I
+(t)
I
max
>>
1,
we have nonlinear modulation,
since the carrier is multiplied by higher powers of
fit).
In case
I
t,h(t)l
<<
1, the exponential modulation is
approximately linear and is given by
e@)
Re{A,[I
+
j@)lexp[j(wct
+
4,)Il
Note that for amplitude modulation we have
eAM(t)
=
Re{A,[1
+
m,g(t)lexp[j
(act
+
4,)Il
Expressing Eq.
1
in the real form, we obtain
e(t)
=
A,[coso,~
+
4c
+
cG(t)]
where for phase modulation
$(t)
=
m,g(t),
mp
=
constant
and for frequency modulation
Nt)
=
mf
[
g(T)dT,
mf
=
constant
The instantaneous frequency
wi(t)
is defined by
In phase modulation, the instantaneous phase of the
modulated signal varies proportionally with the modu-
lating signal
g(t)
ePM(t)
=
A,
COS[Wct
+
mpg(t)I
where
4,
has arbitrarily been set to zero.
coso,t, we have
For single-tone sinusoidal modulation,
g(t)
=
e,&)
=
A,
COS(W,~
+
mp
COSO,~)
where
mP
=
A&
and the peak phase deviation is
independent
of
w,
.
The instantaneous frequency
ai@)
=
d$(t)/dt
=
w,
-
m
w
sinw,t
Pm
and the peak frequency deviation
Aw
=
mpw,
is
proportional to the modulating frequency
w,
.
In frequency modulation, the instantaneous frequen-
cy of the modulated signal is proportional to
g(t)
Oi(t)
=
0,
+
mfg(t)
or
For single-tone sinusoidal modulation
~i(t)
=
W,
+
AOXOSW,~
em@)
=
A,
cos[w,t
+
(mf/w,)
sinw,t]
The peak frequency deviation
A
w
mf
is independent
of
w,,
whereas the peak phase deviation
A
8
=
A
do,
is inversely proportional to
w,;
A
6
(in radians) is the
modulation index, often denoted by
p.
For broad-band
application,
Aw
<<
w,
and
/3
>>
1.
Frequency Spectrum
of
Single-Tone
Angular Modulation
Small Phase Deviation (Narrow-Band PM):
e(t)
=
A,
cos(w,t
+
p
sinw,t),
e(t)
=
A,
(cosw,t
-
p
sinw,t)
p
<<
1
=
A,
COSW,~
-
$(~,p) COS(W,
-
w,)t
z-
+
+(A,/$ cos(w,
+
w,)t
7
The corresponding equation for
AM
is
eAM(?)
=
A,
COSW,I
f
i(A,m,) COS(0,
-
O,)f
+
i(A,m,) cos(w,
+
w,)t
Large
Phase Deviation (Wideband PM):
e(t)
=
A,
cos(w,t
+
p
sinw,t),
p
>>
1
=
A,[cosm,t cos
(p
sinw,t)
-
sinw,t sin@ sinw,?)]
n
I
=
A,[cosw,t
2
Jn(p)
cosnu,t
n=
-m

23-8
REFERENCE
DATA
FOR ENGINEERS
The waveform for wideband modulation is given by
the equation
e(t)
=
Ac{Jo(P)
cosw,t
-JI(p)[cos(w,
-
w,)t
-
cos(w,
+
o,)tl
+
J2(~)[C0S(OC
-
2w,)t
+
cos(w,
+
2w,)t]
-
J~(p)[cos(w,
-
3w,)t
-
cos(w,
+
3w,)t]
+
. .
.
}
=
A,
J~(~)cos(o,
+
no,)l
m
n=
-m
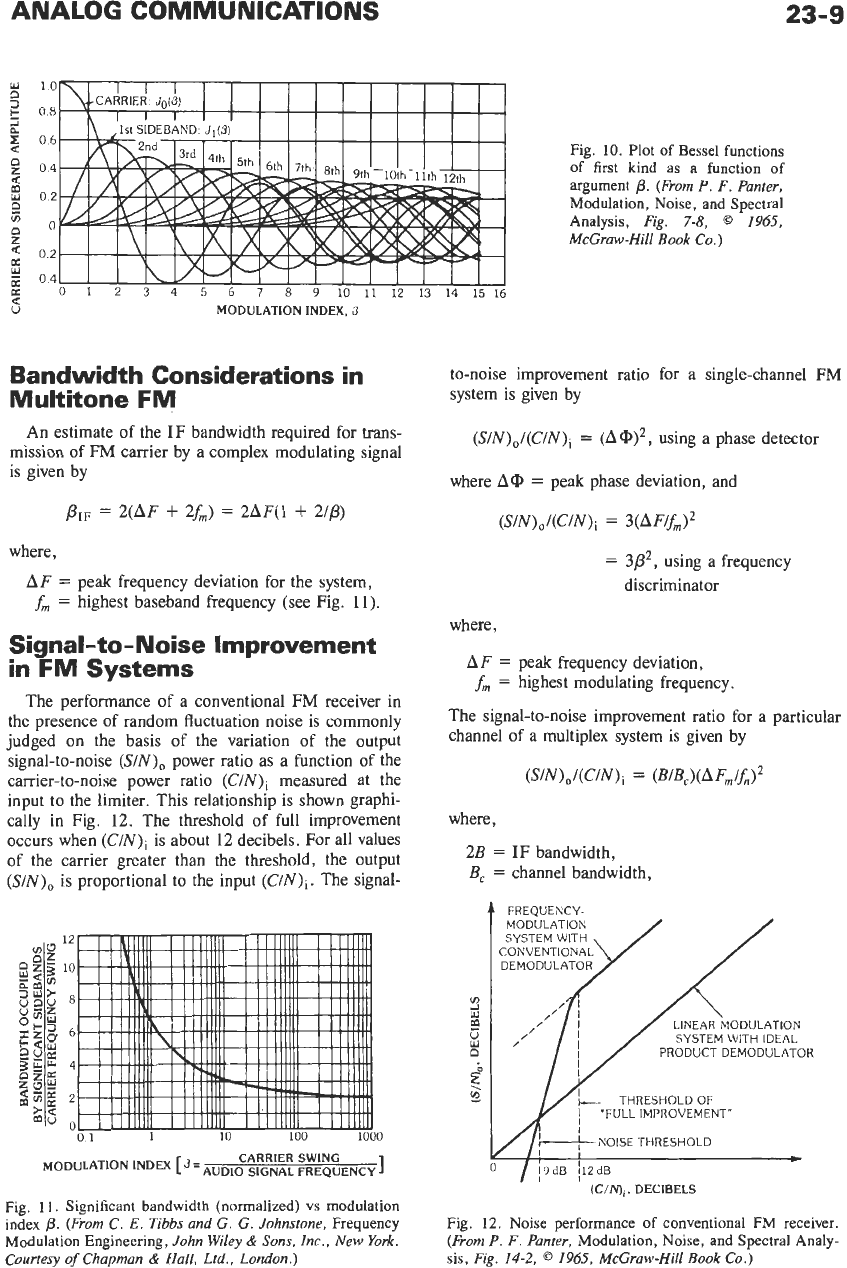
as shown in Fig.
9.
In practical application, the required bandwidth is
finite, for-beyond a certain frequency range from the
carrier, depending on the magnitude of P-the side-
band amplitudes, which are proportional to
In@),
are
negligibly small (see Fig.
10).
Note that at
P
=
2.404,
Jo(p)
=
0
and the carrier amplitude is zero.
The average power in an angle-modulated wave is
constant
m
p
=
;(A:)
c
Jn2m
-m
The spectral components are as follows.
(A)
Carrier:
(B) Sidebands due to
q:
(C) Sidebands due to
w2:
(D)
Beat frequencies at
w,
t
nwl
2
mw2:
Spectral Distribution
of
an
FM/FM
Signal
Let
w,
=
carrier angular frequency,
w,
=
subcarrier,
and
w,
=
modulating angular frequency. The instanta-
neous frequency
of
the carrier wave
is
q(t)
=
w,
+
Am
cos[w,t
+
4,
+
p,sin(w,t
+
4,)]
=
;(A:)
where,
Multitone Angle Modulation
A
w
=
peak frequency deviation of carrier,
P,
=
Aw,/w,
=
peak phase deviation of
For
two-tone angle modulation
with
w1
and
w2,
the
subcarrier.
The spectral distribution is given by
instantaneous frequency is given by
=
W,
+
AW,lt
coswlt
+
Amc*
COSW~I
mcr
40
=
A,
c
c
Jp(P)Jq(PP,)
where
Awcl
and
Amc2
denote the corresponding fre-
P=
-w
4=
-m
quency deviations of
w,,
and the
FM
signal
is
X
cos[(wc
+
pus
+
4wrn)t
+
4c
+
~4s
+
s4ml
e(t)
=
A,
cos(w,t
+
plsinwlt
+
p2sino2t)
where
P
=
Ado,
=
peak phase deviation of carrier.
where
PI
=
AwCllol
and
Pz
=
AwC2/o2.
Fig.
9.
Composition
of
FM wave
into sidebands.
(From P. F.
Punter,
Modulation,
Noise,
and
Spectral Analysis,
Fig.
7-6,
0
1965,
McGraw-Hill
Book
Co.)
ANALOG COMMUNICATIONS
23-9
a
U
06
04
02
0
02
041
1
I
ILV
I
I
I I
I
I I
1
1
I I
I
0
1
2
3
4
5
6
7
8
9
10 11
12
13
14
1516
-
MODULATION
INDEX,
6
Bandwidth Considerations
in
Multitone FM
An estimate of the IF bandwidth required for trans-
mission of FM carrier by a complex modulating signal
is given by
PIF
=
2(AF
+
2fm)
=
2AF(1
+
2/p)
where,
AF
=
peak frequency deviation for the system,
f,
=
highest baseband frequency (see Fig.
11).
Signal-
to
-
Noise Improvement
in
FM
Systems
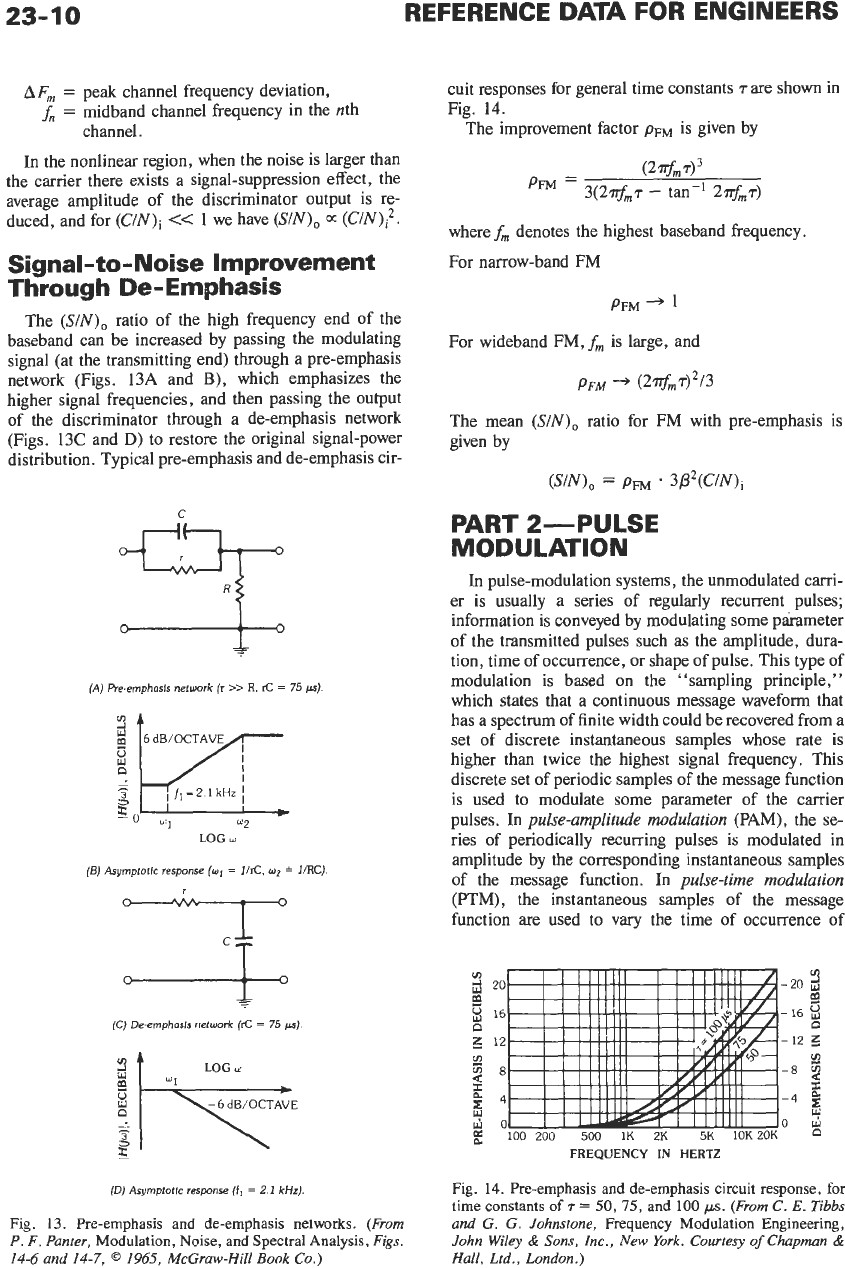
The performance of a conventional FM receiver in
the presence of random fluctuation noise is commonly
judged
on
the basis of the variation of the output
signal-to-noise
(SIN),
power ratio as a function
of
the
carrier-to-noise power ratio
(C/N)i
measured at the
input to the limiter. This relationship is shown graphi-
cally in Fig.
12.
The threshold of full improvement
occurs when
(C/N)i
is about
12
decibels. For all values
of the carrier greater than the threshold, the output
(SIN),
is
proportional to the input
(C/N)i.
The signal-
2
LO
8
6
4
2
00
01
1
10
100 1000
CARRIER
SWING
INDEX
[’=AUDIO
SIGNAL
FREQUENCY
3
Fig. 11. Significant bandwidth (normalized) vs modulation
index
p.
(From C.
E.
Tibbs and
G.
G.
Johnstone,
Frequency
Modulation Engineering,
John Wiley
&
Sons, Znc.,
New York.
Courtesy
of
Chapman
&
Hall, Ltd.,
London.)
Fig. 10. Plot of Bessel functions
of first kind as a function of
argument
p.
(From
P.
F. Punter,
Modulation, Noise, and Spectral
Analysis,
Fig.
7-8,
@
1965,
McGraw-Hill Book Co.)
to-noise improvement ratio for a single-channel
FM
system is given by
(S/N),/(C/N),
=
(A@)’,
using a phase detector
where
A@
=
peak phase deviation, and
(S/N),/(C/N)i
=
3(AF/f,)2
=
3p2,
using a frequency
discriminator
where,
A
F
=
peak frequency deviation,
f,
=
highest modulating frequency.
The signal-to-noise improvement ratio for a particular
channel of a multiplex system is given by
(S/N),/(C/N),
=
(B/B,)(A
F,/f,)’
where,
2B
=
IF
bandwidth,
B,
=
channel bandwidth,
A
FREQUENCY-
MODULATION
SYSTEM
WITH
CONVENTIONAL
PRODUCT DEMODULATOR
0
/
/9dB j12dB
*
(C/N),.
DECIBELS
Fig. 12. Noise performance of conventional FM receiver.
(From
P.
F. Punter,
Modulation, Noise, and Spectral Analy-
sis,
Fig.
14-2,
0
1965,
McGraw-Hill Book
Co.)
23-10
REFERENCE DATA FOR ENGINEERS
AF,
=
peak channel frequency deviation,
f,
=
midband channel frequency in the nth
channel.
In
the nonlinear region, when the noise is larger than
the carrier there exists a signal-suppression effect, the
average amplitude
of
the discriminator output is re-
duced, and for (C/N)i
<<:
1 we have (SIN),
m
(CIN)?.
Signal-to-Noise Improvement
Through De-Emphasis
The (SIN), ratio of the high frequency end of the
baseband can be increased by passing the modulating
signal (at the transmitting end) through a pre-emphasis
network (Figs. 13A and
B),
which emphasizes the
higher signal frequencies, and then passing the output
of the discriminator through a de-emphasis network
(Figs. 13C and
D)
to restore the original signal-power
distribution. Typical pre-emphasis and de-emphasis cir-
(A)
Re-emphasis network
(r
>>
R,
rC
=
75
p).
LOG
w
(E)
Asymptotic response
(0,
=
1hC.
o2
IIRC).
(C)
De-emphasls network
(rC
=
75
pJ
LOG
yl
(0) Asymptotlc response
Ifl
=
2.1
kHz).
Fig.
13.
Pre-emphasis and de-emphasis networks. (From
P.
F. Punter, Modulation, Noise, and Spectral Analysis,
Figs.
14-6
and
14-7,
0
1965,
McGraw-Hill Book Co.)
cuit responses for general time constants
rare
shown in
Fig.
14.
The improvement factor
PFM
is
given by
(2.rrf,7)3
pFM
=
3(2M,~
-
tan-’
2%$,7)
where
f,
denotes the highest baseband frequency.
For narrow-band FM
PFM
+
1
For wideband FM,
f,
is
large, and
PFM
-+
(2~L7)*13
The mean (SIN), ratio for FM with pre-emphasis is
given by
(SIN),
=
pm
.
3P*(CIN),
PART 2-PULSE
MODULATION
In pulse-modulation systems, the unmodulated carri-
er is usually a series of regularly recurrent pulses;
information is conveyed by modulating some parameter
of the transmitted pulses such as the amplitude, dura-
tion, time of occurrence,
or
shape of pulse. This type of
modulation is based
on
the “sampling principle,”
which states that a continuous message waveform that
has a spectrum of finite width could be recovered from a
set of discrete instantaneous samples whose rate is
higher than twice the highest signal frequency. This
discrete set of periodic samples of the message function
is used to modulate some parameter of the carrier
pulses.
In
pulse-amplitude modulation
(PAM), the se-
ries of periodically recurring pulses is modulated in
amplitude by the corresponding instantaneous samples
of the message function.
In
pulse-time modulation
(PTM), the instantaneous samples of the message
function are used to vary the time
of
occurrence of
-20
2
v)
3
20
m m
n
0
5
12
-12
5
3
16
-16
3
$8
-8
2
i4 -4
5
Yo
02
100
200 500 1K 2K 5K 10K20K
FREQUENCY
IN
HERTZ
Fig.
14.
Pre-emphasis and de-emphasis circuit response, for
time constants
of
7
=
50,75,
and
100
ps.
(From C.
E.
Tibbs
and
G.
G.
Johnstone, Frequency Modulation Engineering,
John Wiley
&
Sons,
Inc.,
New
York.
Courtesy
of
Chapman
&
Hall, Ltd.,
London.)

ANALOG COMMUNICATIONS
20
Qm
8
25
23-11
I
some parameter of the pulsed carrier. Pulse-duration,
pulse-position, and pulse-frequency modulation are
particular forms of pulse-time modulation. In
pulse-
duration modulation
(PDM)
,
the time of occurrence of
either the leading or trailing edge of each pulse (or both)
is varied from its unmodulated position by the samples
of the modulating wave. This is also called
pulse-length
or
pulse-width modulation
(PWM). In
pulse-position
(or
phase) modulation
(PPM),
the samples of the modulat-
ing wave are used to vary the position in time of a pulse,
relative to its unmodulated time of occurrence. Pulse-
position modulation is essentially the same as PDM,
except that the variable edge is now replaced by a short
pulse. In
pulse-frequency modulation
(PFM), the sam-
ples of the message function are used to modulate the
frequency of the series of carrier pulses.
The pulse-modulation systems enumerated
so
far are
examples of uncoded pulse systems. In
pulse-code
modulation
(PCM), the modulating signal waveform is
sampled at regular intervals as in conventional pulse
modulation. However, in
PCM,
the samples are first
quantized into discrete steps; Le., within a specified
range of expected sample values, only certain discrete
levels are allowed, and these are transmitted over the
system by means of a code pattern of a series of pulses.
Another example of a code-modulation system is
delta modulation.
As in PCM, the range of signal
amplitudes is quantized, and binary pulses are pro-
duced at the sending end at regular intervals. However,
in delta-modulation systems, instead of the absolute
quantized signal amplitude being transmitted at each
sampling, the transmitted pulses carry the information
corresponding to the derivative of the amplitude of the
modulating signal.
SAMPLING
Sampling
in
the Time Domain
If a signalf(t) is sampled at regular intervals of time
and at a rate higher than twice the highest significant
signal frequency, then the samples contain all the
information of the original signal. The functionf(t) may
be reconstructed from these samples by the use of a
low-pass filter. The reconstruction equation is
O<a<l
wheref(t) is band-limited to
B
hertz, and the samples
are taken at sampling intervals
d2B
seconds apart.
Sampling in the Frequency
Domain
A
time-limited signal
f(t)
that is zero outside the
range
t
I
<
t
<
t2
is completely determined by the values
of the spectrum function
F(
jo)
at the angular-frequency
sampling points given by
w,
=
n[2/(tz
-
tl)]
The function
f(t)
expressed in terms of its sampling
values in the frequency domain is given by the recon-
struction equation
x
exp
[j2mt/(tz
-
tl)]
Sampling
of
a Bandpass
Function
(Bo,
Bo
+
B)
The reconstruction equation forf(t) in terms of its
sampled values is
X
cos2n-Bc(t
-
nT)
where
B,
=
Bo
+
(B/2),
the center frequency of the
bandpass signal, and the permissible values of
T
are
given by
m/2Bo
5
T
5
[(m
+
1)/2(B0
+
B)],
m
=
0,
1,
2,
-
*
-
provided
Bo
#
0.
signal of width
B
is illustrated in Fig.
15.
The minimum sampling frequency for a band-limited
PULSE-AMPLITUDE
MODULATION (PAM)
In PAM, the samples of the message function are
used to amplitude modulate the successive carrier
pulses. When the modulated pulses follow the ampli-
tude variation of the sampled time function during the
sampling interval, the process is called
natural sampling

23-12
REFERENCE
DATA
FOR ENGINEERS
or top sampling. In contrast with natural sampling is
instantaneous or square-topped sampling, where the
amplitude of the pulses is determined by the instantane-
ous
value of the sampled time function corresponding to
a single instant (i.e., center
or
edge) of the sampling
time interval. Pulse-amplitude modulation can be in-
strumented by two distinct methods. The first produces
a variation of the amplitude of a pulse sequence about a
fixed nonzero value
or
pedestal and constitutes double-
sideband amplitude modulation (Figs.
16A
and
B).
In
the second method, the pedestal is zero, and the output
signal consists of double-polarity modulated pulses and
constitutes double-sideband suppressed-carrier modula-
tion (Figs. 16C and D).
Spectra
of
Amplitude-
Modulated Pulses
Double-Polarity
AM
Pulses, Natural
(or
Top)
Sampling-In
the process of natural sampling (or
exact scanning), the modulated pulses follow the sam-
pled time function during the sampling interval. The
unit sampling function (Fig. 16E) consists
of
a train of
unmodulated periodic pulses
of
unit amplitude given by
where,
oo
=
2rjO
=
2dT is the fundamental angular
frequency of the pulse train,
T
is the duration of the pulse,
dT is the duty cycle.
Double-polarity
AM
pulses are obtained by multiplying
the message signal
f(t)
by the unit sampling function
pT(t).
In
case
of
sinusoidal modulation,
f(t)
=
A
cos(w,t
+
+),
and the waveform
of
the
AM
pulses is
given by
f,l(t)
=
f(t)PT(t)
=
(r/T)A cos(w,t
+
4)
x
cos
[(noo
2
o,)t
2
41
In
the general case, the message function
f(t)
is band-
limited, and its spectrum is
F(jw).
The output spectrum
is
(A)
Single-polarlfy pulses
(Bl
Single-polarity flat-top pulses.
(C)
Double-polarity pulses
--
c
A
_----
(D) Double-polarity flat-top pulses
(E)
Unit sumpling function
Fig.
16.
Various shapes
of
amplitude-modulated
pulses.
(From
H.
S.
Black,
Modulation
Theory.
Courtesy
D.
Van
Nostrand Co., Inc., Princeton, N.
J.
)
The spectrum
of
the double-polarity
AM
pulses consists
of the original modulation spectrum and an infinite
number of upper and lower sidebands around
wo
and its
harmonics.
Double-Polarity
AM
Pulses, Instantaneous
(or
Square-Top) Sampling-In
case of sinusoidal modu-
lation, the output waveform is given by
In
the general case, the output spectrum is

ANALOG COMMUNICATIONS
23-13
Single-Polarity
AM
Pulses, Natural Sampling-
For sinusoidal modulation
=
Pdt)
+
fsl(t)
where
mu
is the modulation index. In the general case
F,,(j4
=
P(j4
+
F,,(W
where
P(jo)
is the Fourier transform of
pT(t).
ning-For sinusoidal modulation
Single-Polarity
AM
Pulses,
Instantaneous
Scan-
fs4W
=
PT(t)
+
fs2(t)
In the general case
Fs4(j4
=
P(JW)
+
FSZ(j4
Signal-to-Noise Ratio in PAM
The signal to noise ratio for PAM is
=
irn;
PINoB
where,
P
=
average power of unmodulated
radio-frequency pulse train,
No
=
noise-power density in wattslhertz,
B
=
channel (RF) bandwidth.
Also
(SIN),
=
irn;
(TIT) PlNof,,,
where
f,
=
top frequency of message function. If the
receiver is blocked between pulses to eliminate the noise
in the interpulse period, the
(SIN),
at the output of a
low-pass filter is
(SIN),
=
irn;
PINofm
which is identical to the result obtained for conventional
CW
carrier amplitude modulation.
In practice,
PAM
provides a poorer signal-to-noise
ratio than conventional AM, because the receiver is
unblocked for rather longer than the pulse-duration time
owing to the sloping sides of the pulse.
PULSE-TIME MODULATION
(PTM)
The improvement in signal-to-noise ratio obtained by
the use of time-modulated pulses of constant amplitude
instead of amplitude-modulated pulses led
to
the devel-
opment of systems using pulse-duration and pulse-
position modulation. The sampling associated with
pulse modulation may be either natural or uniform
(periodic). Natural sampling may be defined as a
process of sampling in which the time of sampling
coincides with the time of appearance of the time-
modulated pulse as shown in Fig. 17A. In the process of
natural sampling, the pulse duration
T,
corresponds to
the value
of
the modulating signal
M(t,)
at that instant,
and consequently the sampling intervals
t,
are not equal
but depend on the modulation level. Uniform sampling
may be defined as a process of sampling in which the
variation in the parameter of the pulse
is
proportional to
the modulating signal at uniformly spaced sampling
times. This is illustrated in Fig. 17B, where the width
of the pulses is proportional to the modulating values
M(t,)
which are sampled at equal intervals
t,
=
nq
and
are independent of the modulation process.
Spectra
of
Time-Modulated
Pulses
The spectra of PTM pulses can be derived with
reference to Fig.
18,
where the two cosine waves,
A
and
B,
of angular frequency
u,
are displaced relative to each
other by an amount
T,
the width
of
the unmodulated
pulse. The positive and negative steps that give rise to
the pulse train are assumed to occur at the peaks of
waveforms
A
and
B,
respectively. In the absence of
modulation, the time of occurrence of the positive and
negative steps is given by
o,(t
+
712)
=
2n7r
and
o,(t
-
712)
=
2n7r
>+I)
t
(A)
Natural
sampling.
M[ln-
liT,l
t
in
[E)
Uniform
sampling.
Fig.
17. Pulse-duration modulation.
(From
P.
F. Punter,
Modulation, Noise, and Spectral Analysis,
Fig.
18-14,
@
1965,
McGraw-Hill
Book
Co.)

23-14
REFERENCE
DATA
FOR ENGINEERS
II
I1
Fig.
18.
Modulation process
(modified).
(From
P.
F.
Panter,
Modulation, Noise, and Spectral Analysis,
Fig.
17-14,
0
1965,
McGraw-Hill
Book
Co.)
With natural modulation, the time of occurrence of
the positive and negative steps is given by
or(t
+
r/2)
+
/3
sin(o,t
+
4)
=
2n57
and
w,(t
-
r/2)
+
p
sin(w,t
+
4)
=
2n57
Similarly, with uniform modulation, the time of occur-
rence
or
the position of the leading and trailing edges of
the pulses is determined by
o,(t
+
r/2)
+
p
sin(o,t
+
4)
=
2na
w,(t
-
r/2)
+
p
sin
(o,t
-
r
+
4)
=
2na
-
where,
om
is the modulating frequency,
/3
is the modulation index.
Pulses whose moments of occurrence satisfy these
equations
are
said to be time modulated. In pulse-
frequency modulation,
p
=
A
do,,
and in pulse-
phase (or pulse-position) modulation,
p
is constant
independent of the modulating frequency.
Pulse-Frequency Modulation, Natural
Sam-
pling-A useful expression for an infinite train of
unmodulated pulses is in the form
p&)
=
(A/2aj)
m
k-'
{exp[ jkwr(r/2)]
-
exp[
-$or
(r/2)]}
exp(
jko,t)
k=
-m
where,
A
is the amplitude of the pulses,
or
is the pulse repetition frequency.
Frequency modulation can be taken into account by
substituting for
wrr/2
in the expressions for the leading
and trailing edges in the last equation, the expressions
(err)
+
p
sin (w,t
+
4)
and
l(o,r)
-
p
sin (w,t
+
4)
The frequency-modulated pulse train is then
00
x
(J,(W)
COSkW,t
+
2
J,
(kP)
n=l
x
{cos[(kw,
+
no,)t
+
n41
+
(-1)"
cos[(kw,
-
nw,)t
-
nd]})
This expression may be compared with that for the
spectrum of a frequency-modulated continuous wave
given by
em@)
=
AJ@)
COSO,~
m
+
The conclusions reached are as follows.
cos[(w,
-
nw,)t
-
n+]}
(A)
With pulse-frequency modulation using natural
sampling, the direct-current component of the
pulse spectrum has no sideband of the modulat-
ing frequency.
(B)
The kth harmonic of the pulse-repetition fre-
quency is frequency modulated, the modulation
index being kp.
Pulse-Frequency Modulation, Uniform
Sam-
pling-In this type of modulation, the displacement of
waveform
B
of Fig.
18
from its unmodulated position at
any instant of time
t
will depend on the value of the
modulating voltage at
(t
-
r).
The expression for the
modulated pulse train becomes
Pm(t)
=
(AI%)

ANALOG COMMUNICATIONS
23-15
m
sin(kw,
-
no,)(7/2)
ko,(
d2)
X
coskw,t
+
J,(kp)
k= 1
x
cos[(ko,
+
nw,)t
+
n4
-
nu,
(~/2)]
sin(kw,
-
no,)(7/2)
ko,(7/2)
+
(-1y
>>
x
COS[(kO,
-
nw,)t
-
fl4
f
nw,
(d)]
The conclusions reached
are
as follows.
(A) The direct-current component of the pulse spec-
trum has a sideband of the modulating frequency
of amplitude
(AA
w~/2.n){sin[ o,(T/~)]/o,( d2))
Modulation can therefore be recovered by means
of a low-pass filter.
(B)
The upper and lower sidebands of the kth
harmonic of the pulse-repetition frequency are
not equal in amplitude, whereas in the case of
natural sampling they are equal.
Pulse-Position
(or
Pulse-Phase) Modulation-
The waveform of pulse-phase modulation can be direct-
ly derived from that for pulse-frequency modulation by
substituting w,Td for
p,
where
w,
Td
represents the peak
phase deviation of waveforms
A
and
B,
which is
constant independent of the modulation frequency
0,.
The resulting waveform is the following:
Natural sampling:
Note that each pulse-repetition-frequency harmonic is
phase-modulated, with peak deviation equal to kw,Td.
Also, there is no sideband accompanying the direct-
current component of the pulse spectrum, and hence
modulation cannot be recovered by means of a low-pass
filter.
Uniform sampling:
sin[(kw,( d2)]
m
X
COSkO,t
f
J,(kOJ,T,j)
ko,(7/2)
n=
I
sin(ko,
+
no,)(7/2)
cos[(kw,
+
nw,)t
{
kw,(~/2)
sin(kw,
-
nw,)(7-/2)
ko,(7/2)
+
n4
-
nw,(~/2)]
+
(-l),
This is an equation very similar to that for pulse-
frequency modulation.
Signal-to-Noise Improvement
Ratio
in
PTM
In PDM, the noise manifests itself as jitter in the
leading and trailing edges of the recovered pulses, and
the slopes of the pulse edges influence noise reduction.
A PPM system is affected by noise in the same manner
as a PDM system. For trapezoidal pulses (Figs.
19
and
20), the
SIN
power ratio at the demodulator output is
(SIN),
=
$
(to/7,)2
(A,/g)'
The peak pulse power to mean noise power ratio
is
(GIN),.
=
(A,/a)*
Hence
(SIN),
=
(to/~,)2(C/N)i
Fig.
19.
Pulse-position modulation
of
trapezoidal pulses.
(From P. F. Panter,
Modulation, Noise, and Spectral Analy-
sis,
Fig.
18-26,
@
1965,
McGraw-Hill
Book
Co.)
