Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications

25-18

REFERENCE

DATA

FOR

ENGINEERS

The Gaussian probability distribution

p(x)

=

[I/(&

g)]

exp(-x2/2c?)

plays a major role in information problems. Of all

probability distributions with variance

c?

,

the Gaussian

distribution has the largest differential entropy, given by

H(X)

=

log,

(27re0-7

The differential entropy of a vector of length

n

whose

components are independent identically distributed

Gaussian random variables is

H(X)

=

in

log,

(2.rred)

Consequently, if a Gaussian noise process of ideal

rectangular spectrum is sampled at the Nyquist rate of

2W

samples per second, we say the differential entropy

rate of the source is

W

log2

(27red).

A

Gaussian noise

process whose spectrum is constant for frequencies

below

W

hertz and is zero for larger frequencies is called

band-limited white noise.

Entropy Power

The

entropy power

of a random signal is defined to be

the power of band-limited white noise having the same

differential entropy rate and bandwidth as the original

noise.

If

a random signal has an entropy H(bits), the power

of band-limited white noise having the same entropy

rate is given by

Ne

=

(1/2~e)2,~

The power

Ne

is the entropy power of the random signal.

It should be noted that since white noise has the

maximum differential entropy for a given power, the

entropy power of any random signal is less than or equal

to its actual power.

Capacity

of

a Continuous

Channel

The average mutual information between two contin-

uous random variables

X

and

Y

with joint probability

density function

P(x,

y)

is

Z(X

Y)

=

H(X)

-

H(XJY)

=

H(Y)

-

H(Y1X)

=

H(X)

+

H(Y)

-

H(X, Y)

bits. Even though the differential entropy terms appear-

ing here are not invariant under a coordinate transfor-

mation, their difference is. The mutual information has

a fundamental significance.

A

continuous channel usually has some constraint on

the input probability distribution; an average power

constraint or a peak power constraint is the most

common. Therefore,

p(x)

must satisfy one or more

constraint equations of the form

e(x)p(x)dx

5

S

I:.

where

e(x)

is some nonnegative function. The average

power constraint is

x2p(x)dx

5

S

J

-00

The capacity of the continuous channel is the maxi-

mum value of the average mutual information

max

c

=

I(X,

Y)

P(X)

where the maximum is taken over the set of probability

distributions that satisfy the constraints.

The Additive Gaussian

Noise Channel

Calculation of the capacity can be a difficult task

requiring a computer, but the important case of an

additive Gaussian noise channel subject

to

an average

power constraint can be solved analytically.

The channel output,

Y,

is given by

Y

=

X

+

Z

where

X

is the channel input and

Z

is the noise. Since

X

and

2

are independent,

H(YIX)

=

H(Z),

andZ(X

Y)

=

H(Y)

-

H(Z).

For Gaussian noise,

H(Z)

=

log,

27reN

where

N

is the noise power. Then

max

P(X)

C

=

2W[H(Y)

-

f

log,

2~reNI

Factor 2W converts the units of capacity to bits/second.

Output

Y

has variance

S

+

N

where

S

is

the average

power constraint. Entropy

H(Y)

is largest if

Y

is

Gaussian, which will be true if

X

is Gaussian of

variance

S.

Then

C

=

W

log,

2rre(S

-k

N)

-

W

log1

27reN

=

W

log,

(1

+

S/N)

This is Shannon’s formula for the capacity of the

additive Gaussian noise channel with an average power

INFORMATION THEORY AND CODING

25-19

constraint. The channel input signal that achieves chan-

nel capacity has an amplitude distribution described by

the Gaussian function.

If a channel has additive but non-Gaussian noise and

a power constraint, then the capacity may be difficult to

calculate exactly. However, upper and lower bounds on

the capacity are easy to obtain. At average transmitted

power

S,

the capacity,

C,

in bitslsecond, is bounded by

the inequalities

W

log2

[(S

+

N)/N,]

2

C

2

W

log2

[(S

+

N)/N]

where,

W

is the bandwidth,

N

is the average noise power,

Ne

is the entropy power of the noise.

Waveform Channels

An additive Gaussian noise waveform channel with a

general transfer function is shown in Fig. 18. The

capacity of the waveform channel under Gaussian noise

is equal to the capacity one would obtain if the transfer

function were approximated by many thin ideal rectan-

gular transfer functions of different amplitudes. The

capacity

is

given by the so-called “water-pouring”

formulas, written parametrically in terms of

0.

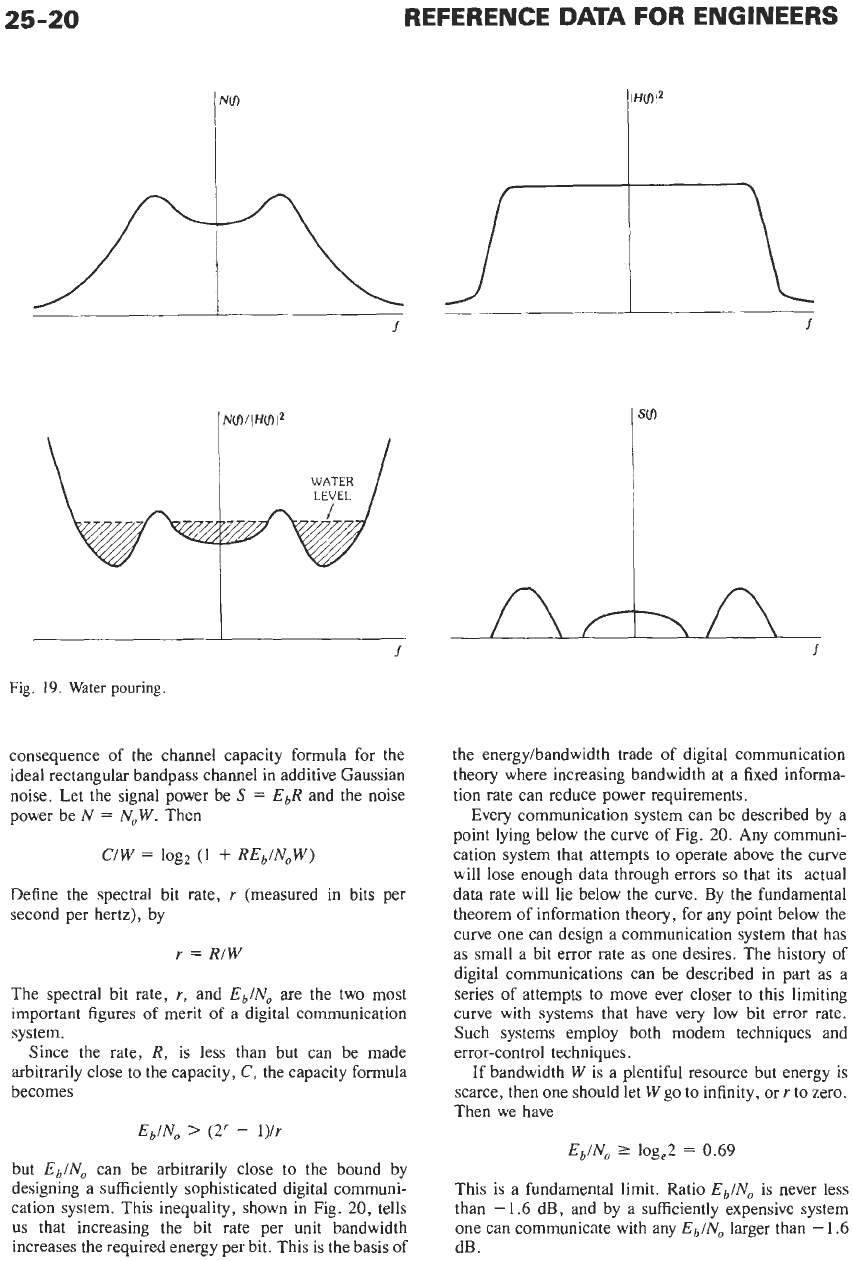
The reason these are called the water-pouring formu-

las can be understood from Fig.

19.

The input informa-

tion is imagined as “poured” into a vessel whose shape

is defined by

H(f)

and

N(f).

This produces the

optimum spectral shape of input waveform

S(f)

=

max[0,

0

-

N(f)l/H(f)I2]

that achieves the channel

nit1

(A)

Conuentronal

model

n;it)

N’W

=NU)/~H(~I*

Xit)

-&TFYit)

(13)

Equlvalent

channel

Fig.

18.

Gaussian-noise waveform channel.

capacity. The important lesson given by the water-

pouring principle is that optimum waveforms put most

of their energy in the spectral region where the channel

is good and little or no energy in the spectral region

where the channel

is

poor. The optimum strategy is

exactly the opposite of an often-used equalization

strategy that “boosts” the skirts of the channel by

adding extra gain there.

Bit

Energy

and

Bit

Error

Rate

The performance of a digital communication system

is measured by the probability of bit error, also called

the

bit

error rate

(BER). On an additive Gaussian noise

channel, the bit error rate can always be reduced by

increasing transmitted power, but it is by the perform-

ance at low transmitted power that one judges the

quality of a digital communication system. The better of

two systems, otherwise the same, is the one that can

achieve a desired bit error rate with the lower transmit-

ted power.

Given a message,

s(t),

of duration

T

containing

K

information bits, the bit energy,

E,,

is given by

where

E,

=

1

s(t)’

dt

is the message energy.

Bit energy

E,

is calculated from the message energy

and the number of information bits at the input to the

encoderlmodulator. At the input

to

the channel, one

may find a message structure in which he perceives a

larger number of bits. The extra symbols may be parity

symbols for error control, or symbols for frame syn-

chronization or channel protocol. These symbols do not

represent transmitted information, and their energy

must be amortized over information bits. Only informa-

tion bits are used in calculating

E,.

For an infinite-length message of rate

R

information

bitslsecond,

Eb

is defined by

E,

=

SIR

where

S

is the message average power.

In

addition to the message energy, the receiver also

sees a white noise signal of one-sided spectral density

No

wattslhertz. Only the ratio

E,INo

or

Eb/No

affects

the bit error rate because the reception of the signal

cannot be affected if both the signal and the noise are

doubled. Signaling schemes are compared by compar-

ing their respective graphs of BER versus required

It

is possible to make precise statements about values

of

EbINo

for which good waveforms exist; these are a

EbIN,.

25-20

REFERENCE

DATA

FOR ENGINEERS

f

Fig.

19.

Water

pouring.

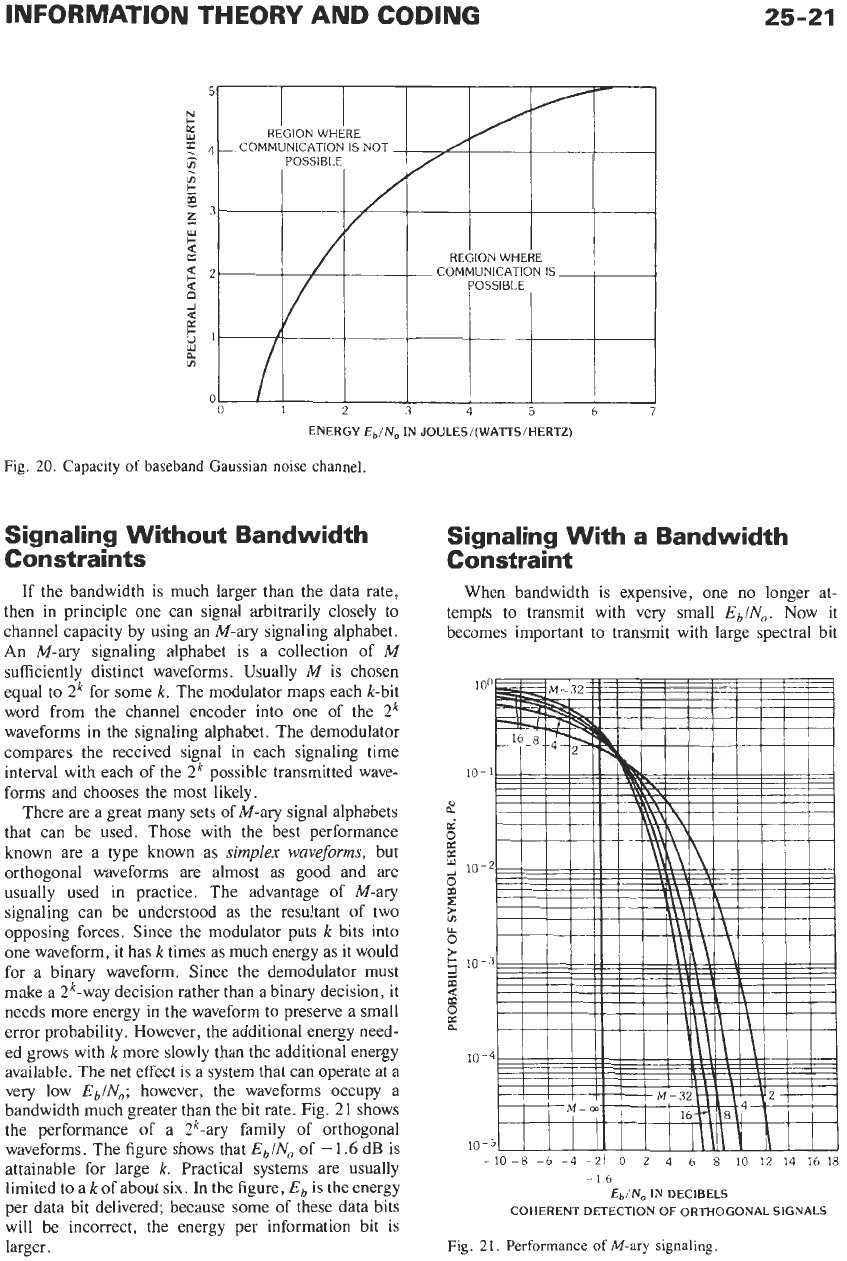
consequence of the channel capacity formula for the

ideal rectangular bandpass channel in additive Gaussian

noise. Let the signal power be

S

=

EbR

and the noise

power be

N

=

NOW.

Then

CIW

=

log2

(1

+

REblNoW)

Define the spectral bit rate,

r

(measured in bits per

second per hertz), by

r

=

RIW

The spectral bit rate,

r,

and

Eb/No

are the two most

important figures

of

merit

of

a

digital communication

sys tem

.

Since the rate,

R,

is

less than but can be made

arbitrarily close to the capacity,

C,

the capacity formula

becomes

Eb/No

>

(2’

-

1)/r

but

Eb/No

can be arbitrarily close to the bound by

designing a sufficiently sophisticated digital communi-

cation system. This inequality, shown in Fig. 20, tells

us

that increasing the bit rate per unit bandwidth

increases the required energy per bit. This is the basis of

I

the energylbandwidth trade of digital communication

theory where increasing bandwidth at a fixed informa-

tion rate can reduce power requirements.

Every communication system can be described by a

point lying below the curve of Fig. 20. Any communi-

cation system that attempts to operate above the curve

will lose enough data through errors

so

that its actual

data rate will lie below the curve. By the fundamental

theorem of information theory, for any point below the

curve one can design a communication system that has

as

small a bit error rate as one desires. The history of

digital communications can be described in part as a

series

of

attempts to move ever closer to this limiting

curve with systems that have very low bit error rate.

Such systems employ both modem techniques and

error-control techniques.

If bandwidth

W

is a plentiful resource but energy is

scarce, then one should let

W

go to infinity,

or

r

to zero.

Then we have

EbIN,

2

10g,2

=

0.69

This is a fundamental limit. Ratio

Eb/N,

is never less

than

-

1.6

dB, and by a sufficiently expensive system

one can communicate with any

Eb/No

larger than

-

1.6

dB

.

INFORMATION THEORY AND CODING

25-21

ENERGY

EhIN,

IN JOULES/(WATTS/HERTZ)

Fig.

20.

Capacity

of

baseband

Gaussian

noise channel.

Signaling Without Bandwidth

Constraints

If the bandwidth is much larger than the data rate,

then in principle one can signal arbitrarily closely to

channel capacity by using an

M-ary

signaling alphabet.

An

M-ary

signaling alphabet

is

a collection of

M

sufficiently distinct waveforms. Usually

M

is chosen

equal to 2k for some

k.

The modulator maps each k-bit

word from the channel encoder into one of the

2k

waveforms in the signaling alphabet. The demodulator

compares the received signal in each signaling time

interval with each of the 2k possible transmitted wave-

forms and chooses the most likely.

There are a great many sets of M-ary signal alphabets

that can be used. Those with the best performance

known are a type known as

simplex

waveforms,

but

orthogonal waveforms are almost as good and are

usually used in practice. The advantage of M-ary

signaling can be understood as the resultant of two

opposing forces. Since the modulator puts

k

bits into

one waveform, it has

k

times as much energy as it would

for a binary waveform. Since the demodulator must

make a 2k-way decision rather than a binary decision, it

needs more energy in the waveform to preserve a small

error probability. However, the additional energy need-

ed grows with

k

more slowly than the additional energy

available. The net effect

is

a

system that can operate at a

very low

EbINo;

however, the waveforms occupy a

bandwidth much greater than the bit rate. Fig. 21 shows

the performance of a 2k-ary family of orthogonal

waveforms. The figure shows that

Eb/No

of

-

1.6

dB is

attainable for large

k.

Practical systems are usually

limited to a

k

of

about six. In the figure,

E,

is

the energy

per data bit delivered; because some of these data bits

will be incorrect, the energy per information bit

is

larger.

Signaling With a Bandwidth

Constraint

When bandwidth is expensive, one no longer at-

tempts to transmit with very small

Eb/N,.

Now it

becomes important to transmit with large spectral bit

Fig.

21.

Performance

of

M-ary signaling.

25-22

REFERENCE DATA FOR ENGINEERS

0

rate,

r

(bits/second)/hertz. Good performance can be

achieved by careful combination of modulation and

error control.

The Ungerboeck convolutional codes are a class of

convolutional codes that provide good combinations of

spectral bit rate and

Eb/No.

The rate

2/3

codes are

designed to work with a set of eight fixed complex

numbers, called a signaling constellation, which repre-

sent phaseiamplitude modulation patterns. Two such

signaling constellations are shown in Fig.

22.

An

encoder for the constraint-length-four Ungerboeck code

for the PSK signaling constellation is shown in Fig.

23.

This code can be used as a plug-in replacement for the

popular uncoded four-phase PSK modulator. The infor-

mation rate is still two bits per symbol. There is no

change in the channel symbol rate,

so

the coded system

has the same bandwidth as the uncoded system and

transmits the same number

of

information bits per

symbol. Hence, the user of the system is unaware of the

presence of the code. However, the system now can run

at a lower

Eb/No

or signal-to-noise ratio; the constraint-

length-four code has a coding gain of

5.7

decibels.

0

DECISION THEORY AND

ESTIMATION THEORY

Decision theory is concerned with the problem of

deciding between a set of hypotheses when given a

collection of imperfect measurements. Estimation the-

ory is concerned with the problem

of

selecting the best

value of a parameter from a continuum of possible

values when given a collection of imperfect measure-

ments. Estimation theory is also concerned with the

selection of a best waveform from a collection of

waveforms when given a collection of imperfect meas-

urements.

General discussion of decision theory and estimation

theory can be found in Davenport and Root* and Van

Trees.

7'

Hypothesis Testing

The simplest problem

of

decision theory, called

hypothesis testing or detection, is to decide between two

mutually exclusive hypotheses. In the case

of

a radar.

*

Reference

14.

i

Reference

15.

Fig.

22.

Two

8-ary

signaling constellations.

0

PSK

2

31T

INPUT

3

BITS

TO

8~ARY

PSK

Fig.

23.

Diagram of encoder for

a

constraint-length-four

Ungerboeck code.

the hypotheses are

target present

or

target absent.

In the

case of signal acquisition, the hypotheses are

signal

present

or

signal absent.

In the general case, the

hypotheses are called the

null hypothesis,

H,,

and the

alternate hypothesis,

HI.

The problem

is

to

decide

which hypothesis is correct by collecting data and

processing them. The data are randomly distributed

with a probability distribution that depends on the true

hypothesis. The set of data may actually be quite

extensive, but it is enough to think

of

it as a simple

measurement whose outcome can only be an element of

a finite set

of

K

elements called the measurement space,

and indexed by

k.

The theory applies to arbitrary data

sets simply by replacing the scalar measurement by an

appropriate vector measurement.

Associated with each hypothesis is a probability

distribution on the measurement space. If

Ho

is true,

then

qOk

gives the probability that

k

will be the

measurement outcome; if

HI

is true, then

qlk

gives this

probability. A simple measurement consists of an

observation of a realization of the random variable. A

measurement is observed, and the problem is to decide

whether hypothesis

H,

or hypothesis

HI

is true.

A

hypothesis testing rule is a partition of the measurement

space into two disjoint sets

Uo

and

Ul

=

Uo'.

If the

measurement is an element

of

Uo,

we decide that

Ho

is

true;

if

it

is

an element

of

U

I,

we decide that

HI

is true.

Each hypothesis testing rule can be described as such a

partition.

Accepting hypothesis

H,

when

HI

actually is true is

called a type-one error, and the probability

of

this event

is denoted by

a.

Accepting hypothesis

HI

when

Ho

actually

is

true

is

called a type-two error, and the

probability

of

this event

is

denoted by

p.

Obviously,

=

c.

qlk

p

=

qOk

k€U,

keU

I

A method for finding the optimum decision regions

is

given by the Neyman-Pearson theorem. This theorem

INFORMATION

THEORY

AND CODING

25-23

expresses the decision regions in terms of a parameter,

T,

called the threshold, and a function called the

log-likelihood ratio given by

[(k)

=

1%

(qOklqlk)

The Neyman-Pearson theorem says that the sets param-

eterized by

T,

Uo(T)

=

{kll(k)

2

T}

Ui(T)

=

{k(Z(k)

<

TI

are an optimum family of decision rules in the sense

that no decision rule can have both type-one error and

type-two error better than any

of

these rules. The

type-one and type-two error probabilities can be traded

by varying the threshold,

T.

The log-likelihood ratio for a block

v

=

(kl,

.

,

k,)

of independent identically distributed measurements

of

length

n

can be written as a sum of per-letter

log-likelihood ratios

because the probability distributions on

v

are products

of the single letter probability distributions

The Neyman-Pearson decision regions for the block

measurement are expressed in terms

of

Z(v)

by the

inequalities

l(v)

<

T

and

Z(v)

2

T.

The same description applies even when the measure-

ments are not independent or identically distributed.

However, the log-likelihood ratio,

I(v),

then cannot be

written as the sum of per-letter log-likelihood ratios.

The expected value of the log-likelihood ratio with

respect

to

qo

is the function known as the

discrimina-

tion.

K-

1

L(q0,ql)

=

2

qOk

log

(qOklqlk)

k=O

The discrimination is closely related to the entropy and

the average mutual information. It is useful for forming

bounds

on

the

probability

of

error.

Estimation Theory

Estimation theory is concerned with the problem of

finding a best value for an unknown parameter when

only imperfect data are available. The estimation

of

the

unknown parameter depends on measurements that are

random variables. The quality of the estimate is limited

by the quality of the measurements. These limitations

can be expressed by means of information-theoretic

bounds; one such bound is known as the Cramer-Rao

inequality.

The simplest estimation problem involves an un-

known real parameter,

0,

to be determined,

and a

random variable,

X.

Understanding this problem leads

to understanding of the more general problems: the

estimation of several parameters based on the observa-

tion

of

a finite number of random variables; the

estimation of several parameters based on observing a

sample waveform of a stochastic process; and the

estimation of a function on an interval based on

observing a sample waveform of a stochastic process.

The random variable has a continuous probability

distribution,

q(x(

e),

conditional on the parameter

8.

The unknown

0

must be estimated based upon an

observation of

X.

The esti-mate of

8

given then mea-

surement

X

is a function

@).

The estimate,

8,

is a

random variable, since it is a function of the random vari-

able

x.

Estimation theory studies various criteria for

maki?g good estimates, that is, for selecting the func-

tion

8(x).

The quality of an estimator

is

judged by its bias

8

=

E[&x)]

and by its variance

Intuitively, one hopes to choose the estimator,

&x),

so

that its bias

is zero and the variance is as small as

possible. Such an estimator is called a

minimum-

variance unbiased estimator.

Sometimes, however, the

minimum-variance unbiased estimator does not exist,

or another estimator has some advantage, and

so

another estimator is used.

The Cramer-Rao bound is a lower bound on the

variance

of

any estimator. For an unbiased estimator of

a single parameter

0,

the most common form of the

bound is

The same bound holds even if

X

is a vector of

measurements. The Cramer-Rao bound can also be

expressed in terms of the discrimination

where,

The Matched-Filter Estimator

Suppose that a known waveform,

s(t),

has spectrum

S(f)

and that additive Gaussian noise has spectral

density

N(f).

The received noisy signal with an un-

known time of arrival

7

is

v(t)

=

s(t

-

T)

+

n(t)

The Cramer-Rao bound says that any estimator of the

time of arrival satisfies

The optimal estimator, if the noise is white and the

signal-to-noise ratio is sufficiently high, is the matched-

filter estimator. It achieves the Cramer-Rao bound. The

matched-filter estimator passes

v(t)

through a filter with

impulse response

s*(-t)

(with some fixed delay to make

it realizable) and estimates

T

from the peak of the filter

output. If the signal-to-noise ratio is not sufficiently

high, then the optimal estimator is not known.

Similar remarks apply to the problem of estimating

the frequency offset,

4,

of an otherwise known band-

pass waveform

v(t)

=

s(t)

cos

[27T(fo

+

4)t

+

e1

+

nR(t)

cos

27rj0t

-

n,(t)

sin

27rjot

where

s(t)

has spectrum

S(

f)

and is a known and finite

energy waveform whose bandwidth is much less than

the known carrier frequency,

fo.

A

small offset in

frequency

4

is to be estimated, and

nR(t),

nI(t)

are

independent covariance stationary Gaussian processes

with identical power density spectrum

N(f),

which is

known. The Cramer-Rao bound says that any estimator

of frequency

4

has an error variance satisfying

where

S‘(

f)

is the derivative of

S(f).

The matched-

filter estimator of frequency consists of a bank of

matched filters. Each filter has impulse response of the

form

s*(-t)

cos

2n(fo

+

A)t

for

A

in a range of

interest. The

A

of the filter with the largest output

provides the estimate of

4.

If the noise

is

white, and the

signal-to-noise ratio is sufficiently high, the matched-

filter estimator achieves the Cramer-Rao bound, and

so

is

optimal. This matched-filter estimator of frequency

offset often can be approximated by a phase-locked

loop. If the signal-to-noise ratio

is

not sufficiently high,

the optimal estimator of frequency is not known.

Maximum Entropy and

Minimum Discrimination

The

Jaynes maximum entropy principle

of data reduc-

tion says that when reducing a set of data into the form

of an underlying model, one should be maximally

noncommittal with respect to missing data. If one must

estimate a probability distribution subject to constraints

on it, then one should choose the probability distribu-

tion of maximum entropy consistent with the con-

straints. For example, if

q(x)

is a probability density

function of a single variable,

x,

and the mean and

variance of

q(x)

are known and otherwise

q(x)

is

unknown, then one should estimate that

q(x) is

a

Gaussian probability density function with the given

mean and variance.

The

Kullback principle

of

minimum discrimination

is

a more general principle that applies when one is given

a distribution,

p(x),

that is a prior estimate of

q(x)

and a

set of constraints on

q(x).

The principle states that, of

the distributions that satisfy the constraints, one should

choose

as

the new estimate that

q(x)

that minimizes the

discrimination

If the probability distribution is discrete and

p(x)

is a

uniform distribution, then this reduces to the maximum

entropy principle.

Spectral Estimation

Spectral estimation is the problem of estimating the

power spectrum of a stochastic process given partial

data, usually only a finite number of samples

of

the

autocorrelation function of limited accuracy. Most

spectral estimation methods in use ignore the noise on

the autocorrelation samples and treat only the problem

of dealing with the missing autocorrelation samples.

The simplest and most popular spectral estimation

procedure is to choose as the estimated spectrum the

Fourier transform of the known values of the autocorre-

lation function, possibly tapering the known values of

the autocorrelation function or padding them with some

zero components. The Fourier transform techniques

implicitly augment the measured components of the

autocorrelation function with artificial components:

either a periodic continuation of the known values or

some zero components.

The Jaynes maximum entropy principle applied to

spectral estimation yields

an

alternative procedure

known as

maximum-entropy spectral estimation.

If

the

correlation samples are given at a set of equispaced lags,

then the maximum entropy estimate of the stochastic

process turns out to be

which is the output of an

autoregressiveJi1ter

excited

by

discrete-time white noise. The filter coefficients are

chosen

so

that the correlation coefficients of this process

agree with the known correlation coefficients. Hence

the filter coefficients are the solution of the matrix

equation

5

hiRi-j

=

-Ri

j=

1

where the correlation coefficients,

Ri,

for

i

=

-L,

. . .

,

L,

are known and

R+

equals

R,.

An

efficient algorithm for solving this set of equations is the

Levinson

algorithm.

SOURCE COMPRESSION

The average amount of information required to

describe a source output symbol is equal to the entropy

of the source. Sometimes it is not convenient or

practical to retain all this information. It then is no

longer possible

to

maintain an exact reproduction

of

the

source. An analog source has infinite entropy,

so

distortion must always be present when the source

output is passed through a channel of finite capacity.

Data compression is the practice of intentionally

reducing the information content of a data record. This

should be done in such a way that the least-distorted

reproduction is obtained. Information theory finds the

performance of the optimum compression of a random

source of data; a naive encoder will have greater

distortion.

The output of a discrete information source is a

random sequence of symbols from a finite alphabet

containing

J

symbols given by

{ao,

al,

.

,

aJ-,}.

A

memoryless source produces the jth letter with proba-

bility

pj

where

pj

is strictly positive. The source output

is

to be reproduced in terms of a second alphabet called

the reproducing alphabet, often identical to the source

alphabet, but not always

so.

For example, the reproduc-

ing alphabet might consist of the union of the source

alphabet and a single new element denoting “data

erased.”

A distortion matrix is a

J

by

K

matrix with nonnega-

tive elements

pjk

for

j

=

0,

.

,

J

-

1

and

k

=

0,

.

,

K

-

1

that specifies the distortion associated

with reproducing the

jth

source letter by the kth

reproducing letter. Without loss

of

generality, it can be

assumed that for each source letter

aj

there is at least

one reproducing letter

bk

such that the resulting distor-

tion

pjk

equals zero. Usually the distortion in a block is

defined as the arithmetic average

of

the distortions of

each letter of the block. This

is

called a per-letter

fidelity criterion.

An

important distortion matrix is the probability-of-

error distortion matrix. For this case the alphabets are

identical. For example, take

J

=

K

=

4

and

[;

j

11

p=llol

This distortion matrix says that each error is counted as

one unit

of

distortion.

A

different data-compression

problem with the same source alphabet and reproducing

alphabet is obtained if one takes the distortion matrix

This distortion matrix says that, modulo four, an error

of two units is counted as two units of distortion.

A source compression block code of blocklength

n

and size

M

is a set consisting of

M

sequences of

reproducing letters, each sequence of length

n.

The

source compression code is used as follows. Each

source output block of length

n

is mapped to that one of

the

M

codewords that results in the least distortion.

The entropy of the output of the data compressor is

less than that of the original source and therefore can be

encoded into a smaller number of bits.

The

Distortion-Rate Function

Data compression is a deterministic process. The

same block of source symbols always produces the same

block

of

reproducing letters. Nevertheless, if attention

is restricted to a single source output symbol without

knowledge of the previous or subsequent symbols, then

the reproducing letter is not predetermined. The letter,

bk,

into which source letter

uj

is encoded becomes a

random variable even though the block encoding is

deterministic. This random variable can be described

by a transition matrix,

Qkb.

Heuristically, we think of

Qkb

as describing an artificial channel that approxi-

mates the data compression. Each time the source

produces letter

a),

it is reproduced by letter

bk

with

probability

Qkb.

To obtain the greatest possible compression, it seems

that this conditional probability should, on average,

result in the smallest possible mutual information

between the source and the reproduction provided that

the average distortion is

less

than the allowable average

distortion. This heuristic discussion motivates the fol-

lowing definition.

The distortion-rate function,

D(R),

is given by

where the minimum is over all probability transition

matrices

Q

connecting the source alphabet and the

reproducing alphabet that satisfy

I(p;Q)

5

R.

The

definition is justified by the source compression theor-

ems of information theory. Intuitively, if rate R bits per

source letter is specified, then any compression must

provide a distortion of at least

D(R).

Conversely,

compression to a level arbitrarily close to

D(R)

is

possible by appropriate selection of the compression

scheme.

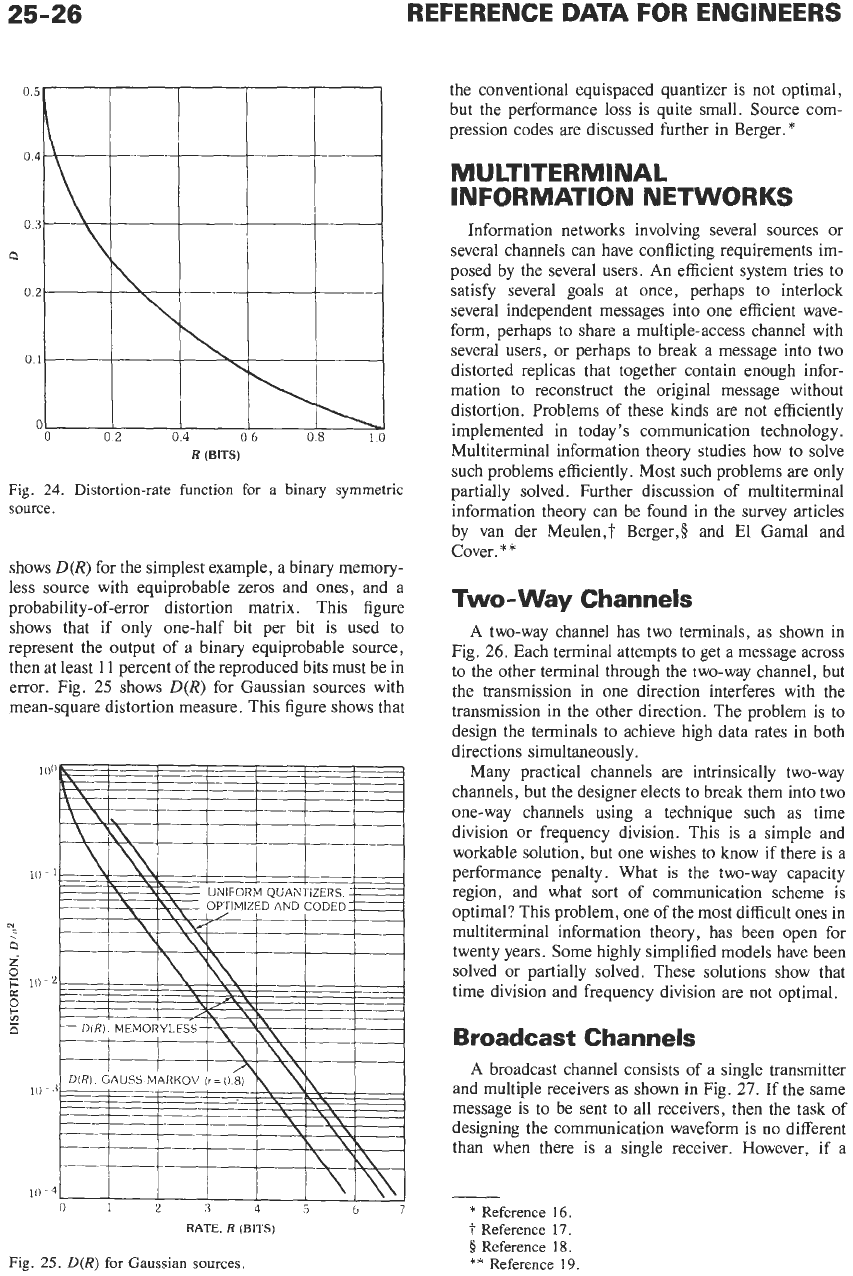
The distortion-rate function can be evaluated analyti-

cally for simple sources and distortion matrices. Fig.

24

25-26

REFERENCE

DATA

FOR ENGINEERS

R

(BITS)

Fig.

24.

Distortion-rate function

for

a

binary symmetric

source.

shows

D(R)

for the simplest example, a binary memory-

less source with equiprobable zeros and ones, and a

probability-of-error distortion matrix. This figure

shows that if only one-half bit per bit is used to

represent the output of a binary equiprobable source,

then at least 11 percent of the reproduced bits must be in

error. Fig.

25

shows

D(R)

for Gaussian sources with

mean-square distortion measure. This figure shows that

IO

N

5

2

0

c

10

E

2

10

1

t

I

Y

\Y

I

-3

0

12

3

4

5

6

7

RATE.

R

(BITS)

Fig.

25.

D(R)

for

Gaussian

sources.

the conventional equispaced quantizer

is

not optimal,

but the performance loss is quite small. Source com-

pression codes are discussed further in Berger.

*

MULTITERMINAL

INFORMATION

NETWORKS

Information networks involving several sources or

several channels can have conflicting requirements im-

posed by the several users.

An

efficient system tries to

satisfy several goals at once, perhaps to interlock

several independent messages into one efficient wave-

form, perhaps to share a multiple-access channel with

several users, or perhaps to break

a

message into two

distorted replicas that together contain enough infor-

mation to reconstruct the original message without

distortion. Problems of these kinds are not efficiently

implemented in today’s communication technology.

Multiterminal information theory studies how to solve

such problems efficiently. Most such problems are only

partially solved. Further discussion of multiterminal

information theory can be found in the survey articles

by van der Meulen,? Berger,# and El Gama1 and

Cover.

*

Two-way

Channels

A

two-way channel has two terminals, as shown in

Fig.

26.

Each terminal attempts to get a message across

to the other terminal through the two-way channel, but

the transmission in one direction interferes with the

transmission in the other direction. The problem is

to

design the terminals

to

achieve high data rates in both

directions simultaneously.

Many practical channels are intrinsically two-way

channels, but the designer elects to break them into two

one-way channels using a technique such as time

division or frequency division. This is a simple and

workable solution, but one wishes to know if there

is

a

performance penalty. What is the two-way capacity

region, and what sort of communication scheme is

optimal? This problem, one of the most difficult ones

in

multiterminal information theory, has been open for

twenty years. Some highly simplified models have been

solved or partially solved. These solutions show that

time division and frequency division are not optimal.

Broadcast Channels

A

broadcast channel consists

of

a single transmitter

and multiple receivers as shown in Fig.

27.

If the same

message is to be sent to all receivers, then the task of

designing the communication waveform is

no

different

than when there is a single receiver. However, if a

*

Reference

16.

1-

Reference 17.

8

Reference 18.

**

Reference

19.

INFORMATION THEORY AND CODING

I

SOURCE

I

ENCODER

I

1

I

25-27

I

&

I I

I

r------------1

r------------,

I

TERMINAL

1

I

TERMINAL2

\

I

1-

I

1

I

1

I

USER

-

DECODER

I

CHANNEL

I

I I

tj-

I

ENCODER

I

SOURCE

I

‘r2

-2

different message is to be sent to each receiver, the

problem is more complex. Conventionally, the channel

is divided according to the needs of the receivers, using

time-division or frequency-division signaling tech-

niques. Optimum techniques are more tightly inter-

locked and do better.

Time-division or frequency-

division multiaccess signaling cannot achieve the capac-

ity region of a broadcast channel.

BROADCAST

TRANSMITTER

Degraded Diversity Systems

-’

.

A

diversity system

sends the same information to a

user twice through two channels

so

that if one channel is

broken, the message will still arrive.

A

degraded

diversity system

is more subtle. It sends half the message

through each of two channels but in such a way that

either half suffices to reconstruct a degraded copy of the

message.

A

high-fidelity reproduction is obtained if

both channels are intact; a low-fidelity reproduction is

obtained if only one channel is intact. The simplest

model of a degraded diversity system is shown in Fig.

28.

The theory shows that the data can be encoded

so

that either side channel can reconstruct the data from

the half-rate code with a probability of error of

20.7

percent, and no better encoding exists.

.

RECEIVER

n

-N

RECEIVER

w

Fig.

27.

Broadcast

channel.

Remote Compaction

of

Dependent Data

A

fundamental multiterminal source coding problem

is shown in Fig.

29.

Data sources

X

and

Y

are

dependent. The data are to be sent to a common site at

rates R, and R,, but the encoders do not communicate

with each other. The admissible rate region is shown in

Fig.

30.

Encoder/decoders can be built with rate pairs

corresponding to any point in the upper-right region.

It

is quite remarkable that this region would not be any

larger even if the two encoders could each see the output

of both sources.

THE

COMMUNICATION

GAMES

The communication problem is given a new dimen-

sion of complexity and becomes a two-person game

when an adversary is introduced. The theory that is then

developed has its roots in both information theory and

game theory. The transmitter and receiver together

constitute one player, or team, and the adversary is the

second player. The adversary may have a variety of

purposes. It may be his goal to interrupt communica-

tion, in which case he is called a jammer or a spoofer; it

may be his goal to determine the specific message

transmitted, in which case he is called a wiretapper or

eavesdropper; it may be his goal simply to detect the

existence of communication, in which case he is called

a monitor; or it may be his goal to determine the

location of the transmitter, in which case he is called a

locator.

The

Jammer Saddle Point

The jamming game is a game played by the jammer

and the transmitter. The jammer selects the noise

or

interference properties of the channel. That is, the

jammer selects a probability transition matrix,

Q,

connecting the input and output alphabets. The trans-

mitter designs a communication waveform without

knowledge of which channel noise was selected by the

jammer. Variations are possible wherein the jammer

Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications

Подождите немного. Документ загружается.