Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications

25-8

REFERENCE

DATA

FOR ENGINEERS

State

SO

Fig.

6.

Trellis diagram

of

r

=

2,

s

=

7

run-length-limited channel.

previous symbols. If previously selected symbols influ-

ence the selection of a symbol, then the source is said to

possess memory. If the selection of a symbol is

influenced only by the immediately preceding symbol,

the source is known as a

Markov source.

If

the selection

is influenced by the

m

previously selected symbols, the

source

is

called an

mth-order Markov

source.

The

Entropy

Function

If a source output

ai

occurs with probability

p(aj),

then the amount of information associated with the

known occurrence of the event is defined to be

qui)

=

-logp(uj)

In the definition, when logarithms are to the base

2,

the

information

is

measured in units of

bits.

When loga-

rithms are taken to the base

e,

the information is

measured in units

of

nuts

(a shortened form

of

natural

units). Usually, the nat is more convenient for theoreti-

INFORMATION WORDS CODEWORDS

11 0100

10 1000

000 000100

010 001000

011

100100

0010 00001000

0011 00100100

Example:

1101010

-

01000010001000

Fig.

7.

The

r

=

2,

s

=

7

Franaszek

rate one-half code.

cal developments, and the bit is more convenient for the

final result. The conversion factor is: one nat equals

1.443

bits.

If the probabilities of selecting the source symbols

are

p(uO),

p(al),

.

,

P(U~-~),

respectively, then the

information generated each time a symbol is selected

is

-log2

p(uj)

bits. Since the symbol

ai

will, on average,

be selected

np(uj)

times in a total of

n

selections, the

average amount of information obtained from

n

selec-

tions is

nP(ao)

log2

P(ao1-I

+

’

.

,

+

nP(a.I-l)

log2

p(aJ-l)-l

bits. Divide by

n

to obtain the average amount of

information per symbol selection. This

is

known as the

average information,

the

uncertainty,

or the

entropy,

WP).

.I-1

j=O

H(p)

=

-

p(ui)

log,

p(uj)

bitsisymbol

or

J-

I

H(P)

=

-

c

Pj

1%

pj

j=O

where

pj

is

an abbreviation of

p(a,).

The entropy associated with

n

selections from the

statistically independent set is equal to

n

times the

entropy per single selection. The term entropy is used

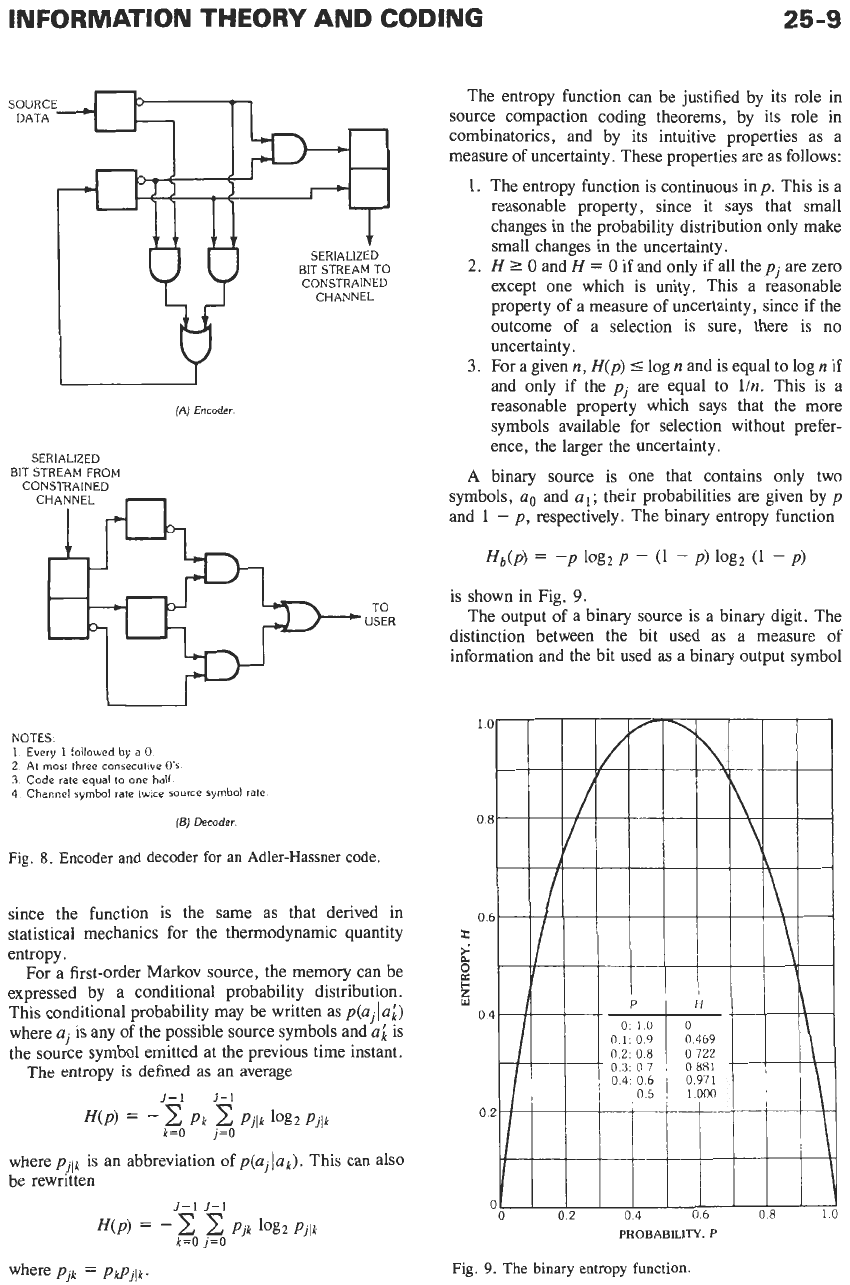
INFORMATION THEORY AND CODING

25-9

SOURCE

DATAc

+

SERIALIZED

BIT

STREAM

TO

CONSTRAINED

(1

CHANNEL

(A)

Encoder

SERIALIZED

BIT

STREAM FROM

CONSTRAINED

SERIALIZED

BIT

STREAM FROM

CONSTRAINED

CHANNEL

TO

USER

NOTES.

1.

Every

1

lollowed by a

0

2.

At most three consecutive

Os

3.

Code rate

equal

to one

half.

4

Channel symbol rate twice

SOUTCB

symbol rate

(B)

Decoder

Fig.

8.

Encoder and decoder for an Adler-Hassner code.

sinte the function is the same as that derived in

statistical mechanics for the thermodynamic quantity

entropy.

For a first-order Markov source, the memory can be

expressed by a conditional probability distribution.

This conditional probability may be written as

p(aj

la;)

where

aj

is any of the possible source symbols and

a;

is

the source symbol emitted at the previous time instant.

The entropy

is

defined as

an

average

where

pjik

is

an abbreviation of

p(ajlak).

This can also

be rewritten

I-1

J-1

H(p)

=

-

Pjk

log2

Pjlk

k=O

j=O

The entropy function can be justified by its role in

source compaction coding theorems, by its role in

combinatorics, and by its intuitive properties as a

measure of uncertainty. These properties are as follows:

1.

The entropy function is continuous in

p.

This is a

reasonable property, since it says that small

changes in the probability distribution only make

small changes in the uncertainty.

2.

H

2

0

and

H

=

0

if and only if all thepj are zero

except one which is unity. This a reasonable

property of a measure

of

uncertainty, since if the

outcome of a selection is sure, there is no

uncertainty.

3.

For a given

n,

H(p)

5

log

n

and is equal to log

n

if

and only if the

pj

are equal to

lln.

This is a

reasonable property which says that the more

symbols available for selection without prefer-

ence, the larger the uncertainty.

A

binary source is one that contains only two

symbols,

a.

and

al;

their probabilities are given by

p

and

1

-

p,

respectively. The binary entropy function

Hb(p)

=

-P

log2

P

-

(1

-

P)

log2

(1

-

P)

is shown in Fig.

9.

The output of a binary source is a binary digit. The

distinction between the bit used as a measure of

information and the bit used as a binary output symbol

1c

OE

Ot

r

!i

2

OL

z

02

0

PROBABILITY.

P

Fig.

9.

The binary entropy function

25-10

REFERENCE

DATA

FOR ENGINEERS

should be carefully noted. Fig.

9

shows that on average

the amount of information provided by a binary source

is always equal to or less than 1 bit/bit (one bit of

information per data bit). The binary source provides

one bit of information for each selected symbol only

when the two symbols are equiprobable.

Source Encoding

The entropy function can be interpreted as the

average amount of information necessary to specify

which symbol has been produced by the source. If a

source selects

n

symbols, where

n

is a very large

number, then with high probability, it will select a

sequence from the set of

ZnH

different typical sequences

each having a probability of occurrence of about

(1/2)"H. This is a direct physical interpretation of

H.

It

means that, theoretically,

a

very long typical sequence

of

n

q-ary symbols selected by the source can be

encoded and retransmitted using only

nH

binary digits,

each carrying one bit of information.

Usually, the binary codeword will be embedded in

some longer binary text. Sometimes punctuation sym-

bols are used and

are

not counted as part of the

codeword. However, the more enlightened view is to

incorporate the punctuation symbols into the code

alphabet and devise an even more compact code. Then

the code must be a self-punctuating code. Symbols to

punctuate the code become implicit to the codeword.

Fixed-Length Block Codes

A

fixed-length block code needs no punctuation.

Compaction of a source with

J

symbols encodes

n

source output symbols into a codeword of length

k

bits,

where

n

and

k

are fixed. There are

J"

possible source

output blocks the length

n,

so

the blocklength of a

binary code must be log,

d"

bits if every possible output

block is to be encoded. This requires log,

J

codeword

bits per source output symbol. In general, this is much

greater than the source entropy rate.

A

fixed-length block code can encode at the entropy

rate but then must allow the possibility of an error.

A

source compaction block code with rate a little above

the entropy provides only

n(H(p)

+

E)

bits,

so

2"(H(P)

+

codewords are assigned to the "typical"

source output blocks-those blocks of greatest proba-

bility. By picking

n

large, the probability

of

a nontypi-

cal-hence noncodable-source output block can be

made many orders of magnitude smaller than the

probability of failure

of

the equipment.

A

fixed-length

block code for source compaction must rely on this kind

of reliability argument in order to encode at a rate near

the entropy.

Variable-Length Block Codes

A

variable-length block code encodes

n

source output

symbols into

k

channel symbols, where either

n

or

k

is

variable. The Huffman codes constitute the most com-

mon example. For them,

k

is variable and depends on

the particular block of

n

symbols observed, while

n

is

fixed.

The variable-length codewords of a Huffman code

are constructed from knowledge of the probabilities of

each of the

J"

source output blocks of length

n.

We will

construct a simple example using

n

=

1.

The construc-

tion, illustrated in Fig.

10,

proceeds as follows.

For convenience, the symbols are listed in order

of

decreasing probability. The two symbols of lowest

probability are merged into a single symbol whose

probability is the sum of the two constituent probabili-

ties. At each step, this same procedure is repeated,

merging two symbols into one symbol and adding their

probabilities. The process stops when one symbol

remains. Finally, read the tree from right to left,

labeling the branches that leave each node either with a

zero or with a one. The codeword is the string of labels

from the rightmost node back to the original symbol.

A

Huffman code can be formed just as easily for

blocks of length

n.

Simply replace the source symbols

in the construction with blocks of source symbols, and

replace the symbol probabilities with probabilities of

blocks. By choosing a large enough n-usually an

n

quite small will do-the average codeword length can

be made as close to the source entropy as desired, and

so

a nearly optimal Huffman code can be constructed.

A

Huffman code is a prefix code, sometimes said to

be self-punctuating. It needs no explicit punctuation.

Successive

n

blocks of source symbols can be encoded

one after the other and concatenated. By decoding the

codewords in a first-in, first-out fashion, the source

symbols are uniquely recovered.

Variable-Length Tree Codes

A

variable-length tree code for source compaction

encodes indefinitely long strings of source output sym-

bols into indefinitely long strings of code symbols. The

encoding operation has a sliding structure whereby, as a

Source

Symbol

00

01

02

03

04

05

0

40

-0

40

-0

40

-0

40

0

30

-

0

30

-0

30

-0

30

0

20

-

0

20-0

20

002

*

0

04

Source

Symbol

Codeword

00

1

01

00

02

010

03

0111

a4

01100

05

01101

Average

codeword

length

=

2

06

bmary

d!gds/symbol.

The

entropy

of

the

source

=

1

999

biis/syrnbol.

Fig.

10.

Example

of

Huffman

encoding.

INFORMATION THEORY AND CODING

25-1

1

00

01

10

few source symbols enter the encoder, a few codeword

bits leave the encoder. The relationship between the

number of symbols entering the encoder and the number

of bits leaving it is variable, depending

on

the particular

source symbols to be encoded.

One of the earliest variable-length tree codes for

source encoding is the Elias code. Because

of

its

simplicity, it is an excellent tutorial example. We

describe

an

Elias code for a binary source with binary

source alphabet

{ao,

a

I}

and probability distribution

p

=

(0.7,

0.3). The entropy of this source is

0.88

bit. Imagine that the semi-infinite sequence of source

output bits is a binary representation of a real number,

r,

in the interval

[0,

11.

Refer to Fig.

11.

The first sym-

bol tells whether

r

is in the interval

[0,

0.71 or in the

interval [0.7,

11.

This interval is itself subdivided in

the same proportion, and the next source bit selects

one of these two intervals. At each iteration, the pro-

cess repeats, and, in this way, the process continues

indefinitely.

The codeword, on the other hand, is a conventional

binary representation of point

r.

As soon as enough

source symbols are received to determine whether

r

is in

the interval

[0,

0.5)

or the interval

[0.5,

11,

a codeword

bit can be transmitted. The encoding is variable length

since the number of source symbols needed to produce

one codeword bit is random.

The decoder can begin its task after receiving only a

few codeword bits. For example, if the binary sequence

starts with

011

. . .

,

the point represented must lie

between 0.375 and

0.50;

hence the first symbol from

the source must be

ao.

If the binary sequence starts with

01

10,

the point represented must lie between 0.375 and

11

0

10

.

0

(A)

Description

of

I

by

sourceword

(E)

Descrlptlon

of

r

by

codeword.

Fig.

11.

Construction of

an Elias

code.

0.4375; hence the first three symbols from the source

must be

aOaOa

I.

The Elias code is not practical because of precision

problems. Errors in early calculations, no matter how

small, will eventually cause encoding and decoding

errors. A practical variable-length tree code, due to

Pasco and Rissanen,* is available, but the description is

more difficult.

Universal Codes

A source compaction code usually requires a proba-

bilistic model of the source in order to attain its best

performance. The encoder will encode to near the

entropy of the source only if it is given a satisfactory

model of the source. Some source compaction codes,

called

universal source codes,

implicitly construct their

own model of the source as they go along (assuming

that past source sequences are representative of future

sequences) and

so

encode near the entropy

of

whatever

source they are given.

The Lempel-Ziv code is a universal variable-to-fixed-

length source-compaction block code that does not

require an externally constructed source model. The

technique, illustrated in Fig.

12,

is to break up the

string of source output symbols into substrings of

variable length but not longer than a largest allowed

length. The encoder has a buffered copy of the raw data

that has already been encoded. At each iteration, it

searches for a prefix of the data yet waiting to be

encoded within the data already encoded. The longest

prefix of which a copy can be found among the symbols

recently encoded, together with one more innovation

symbol, becomes the next substring.

A substring

is

encoded in three parts: a binary-

encoded pointer telling where a copy of the substring

begins within recently encoded data; a binary-encoded

number giving the length of the substring; and the value

of the innovation symbol. By including an innovation

symbol, the encoder cannot degenerate into an unen-

codable situation.

The Lempel-Ziv decoder must keep a copy of recent-

ly decoded data in which it

looks

to recreate subsequent

substrings that it must decode. The decoder contains a

finite-length buffer equal in length to the encoder

finite-length buffer. In decoding a substring, the decod-

er buffer contains the same symbols that the encoder

buffer contained when that substring was encoded.

Hence, the decoder can use the pointer and the sub-

string length to reconstruct the next substring.

CODING FOR DISCRETE

NOISY CHANNELS

The deep-space Gaussian noise channel and the noisy

binary channel are two important examples of noisy

channels. The first example

is

a continuous-time, con-

tinuous-amplitude channel that is usually made into a

*

Reference

5.

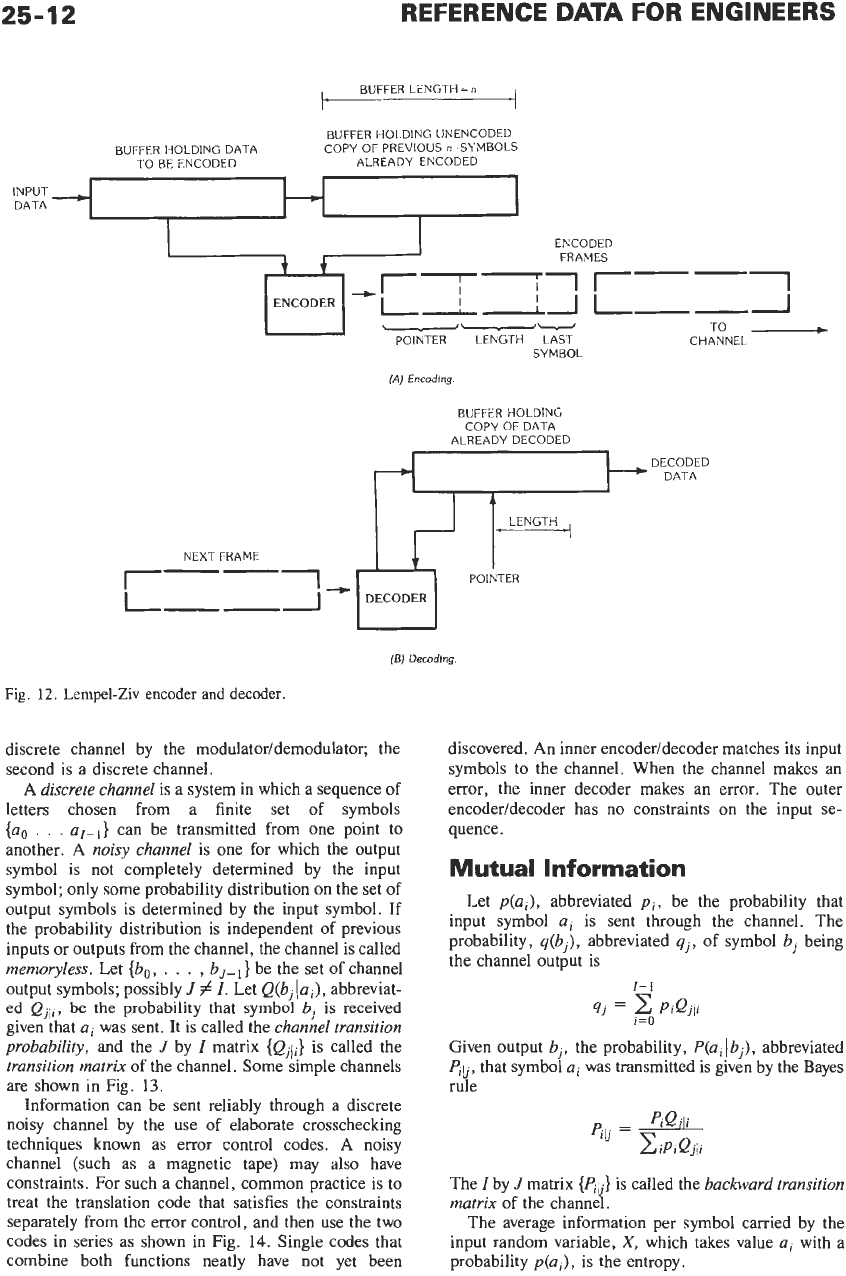
25-12

NEXT FRAME

REFERENCE

DATA

FOR ENGINEERS

I

LENGTH

BUFFER LENGTH

=

n

I I

BUFFER HOLDING UNENCODED

COPY OF PREVIOUS

n

-SYMBOLS

BUFFER HOLDING DATA

TO BE ENCODED ALREADY ENCODED

ENCODED

FRAMES

-1

ll

I-

I!II

L--l

-I-

TO

L

CHANNEL

I

I---.--+-

POINTER LENGTH LAST

SYMBOI

(A)

Encoding.

BUFFER HOLDING

COPYOFDATA

ALREADY DECODED

(E)

Decoding.

Fig.

12.

Lempel-Ziv encoder

and

decoder.

discrete channel by the modulator/demodulator; the

second is a discrete channel.

A

discrete channel

is a system in which a sequence of

letters chosen from a finite set of symbols

{ao

. . .

a[-,}

can be transmitted from one point to

another.

A

noisy channel

is one for which the output

symbol is not completely determined by the input

symbol; only some probability distribution on the set of

output symbols is determined by the input symbol. If

the probability distribution is independent

of

memoiyless.

Let

{bo,

.

,

b,-,}

be the set of channel

output symbols; possibly

J

#

I.

Let

Q(bjlai),

abbreviat-

ed

Qjii,

be the probability that symbol

bj

is

received

given that

ai

was sent. It is called the

channel transition

probability,

and the

J

by

I

matrix

{ej\!}

is called the

transition matrix

of the channel. Some simple channels

are

shown in Fig. 13.

Information can be sent reliably through a discrete

noisy channel by the use

of

elaborate crosschecking

techniques known as error control codes.

A

noisy

channel (such as a magnetic tape) may also have

constraints. For such a channel, common practice is to

treat the translation code that satisfies the constraints

separately from the error control, and then use the two

codes in series as shown in Fig. 14. Single codes that

combine both functions neatly have not yet been

discovered. An inner encoderldecoder matches its input

symbols to the channel. When the channel makes an

error, the inner decoder makes an error. The outer

encodeddecoder has no constraints

on

the input se-

quence.

Mutual

Information

Let

p(ai),

abbreviated

pi,

be the probability that

input symbol

a,

is sent through the channel. The

probability,

q(bj),

abbreviated

qj,

of symbol

b,

being

the channel output is

I-

1

Given output

bj,

the probability,

P(ai

lbj),

abbreviated

plb,

that symbol

ai

was transmitted is given by the Bayes

rule

The

I

by

J

matrix

{elj}

is called the

backward transition

matrix

of the channel.

The average information per symbol carried by the

input random variable,

X,

which takes value

a,

with a

probability

p(ai),

is the entropy.

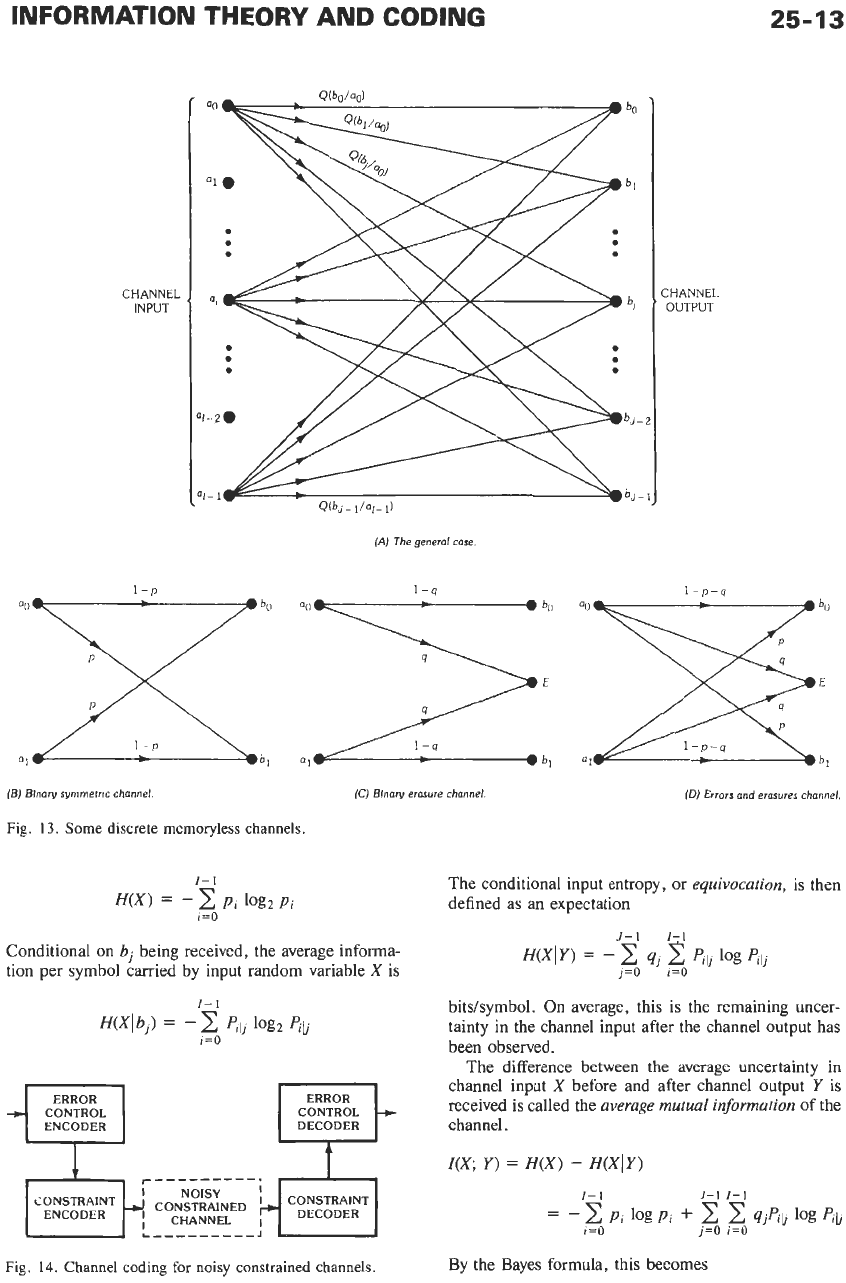
INFORMATION THEORY

AND

CODING

25-13

CHANNEL

INPUT

1-0

(A)

The general case.

1-0

CHANNEL

OUTPUT

(Bj

Blnary symmetric channel.

(C)

Blnary erasure channel.

(0)

Errors and erasures channel.

Fig.

13.

Some discrete memoryless channels.

I-

1

H(X)

=

-

pi

log2

pi

i=O

Conditional on

bj

being received, the average informa-

tion per symbol carried by input random variable

X

is

I-

1

i=O

H(Xlbj)

=

--E

pllj

log*

plk

CONTROL

ENCODER

CONTROL

DECODER

CONSTRAINT

NOISY

CHANNEL

I

‘::zEr

CONSTRAINED

4

DECODER

1

-

L

----_--__

J

-

Fig.

14.

Channel coding for

noisy

constrained

channels.

The conditional input entropy, or equivocation,

is

then

defined as an expectation

bitshymbol. On average, this is the remaining uncer-

tainty in the channel input after the channel output has

been observed.

The difference between the average uncertainty in

channel input

X

before and after channel output

Y

is

received is called the average mutual information

of

the

channel.

Z(X;

Y)

=

H(X)

-

H(XIY)

I-

I

J-I

1-1

=

-

pi

log

pi

+

C.

4jp1.k

log

p1.k

i=O

j=o

By the Bayes formula, this becomes

REFERENCE

DATA

FOR ENGINEERS

C=l-q

bits per input symbol. This is somewhat surprising,

since it says that the erasures cause a loss in capacity

exactly equal to the fraction of symbols erased despite

the fact that the encoder does not know which

nq

symbols will be erased. The capacities of these two

simple channels are shown in Fig.

15.

The average mutual information is a measure of the

average amount of information about the channel input

that can be received by the user by observing the symbol

at the output of the channel.

The average mutual information has a number of

important and satisfying properties:

Error-Control Codes

Average mutual information is nonnegative and is

strictly positive unless the channel output is inde-

pendent of the channel input.

If

I

=

J

and the channel is noiseless (i.e., Qjji

=

1

if

j

=

i),

then

I(X,

Y)

=

H(X),

and the average

mutual information between the output and the

input of the channel is equal to the average

information into the channel.

Average mutual information is symmetric in

X

and

Y.

That is

I(X;

Y)

=

Z(Y;

X)

where

Y

j=O

Z(Y;

X)

=

I-

I

Channel Capacity

The channel capacity,

C,

is defined to be the

maximum rate at which information can be transmitted

through a channel. The fundamental theorem

of

infor-

mation theory says that at any rate below channel

capacity, an error control code can be designed whose

probability of error is arbitrarily small. Intuitively, in a

well-designed message, an isolated channel input sym-

bol

a,

should occur with a probability

pi

such that the

average mutual information is maximized.

For the noisy channel, with transition matrix Q, the

channel capacity,

C,

is expressed mathematically by

where the maximum is over all probability distributions

on the input alphabet. For simple channels, the capacity

can be evaluated by finding the maximum analytically.

For

more difficult channels,

efficient

computational

algorithms exist.

The capacity of the binary symmetric channel with

transition matrix

is

c

=

1

+

p

log,

p

+

(I

-

p)

log* (1

-

p)

bits per input symbol. The capacity of the binary

erasure channel with erasure probability

q

is

~~

Powerful codes are now available for use with

q-ary

symmetric channels whenever

q

is a prime or a prime

power. Codes in use can achieve extremely small

probability of symbol error, but the known codes are

not good enough to achieve code rate near the channel

capacity. Error control codes are routinely used for

many purposes: to reduce required link signal-to-noise

ratio; to protect against various forms of pulsed and

other interference; to protect against hostile interference

in military systems; to protect against noise and media

defects in magnetic recording systems; and

so

forth.

Error-control codes in common use work with a code

alphabet of size

2"

where

rn

is a positive integer. Form

equal to eight, the code alphabet consists of the set of

all eight-bit bytes. It is common to use byte-organized

codes because errors in practical systems tend to occur

in bursts and because the hardware is simpler.

Error-control codes can be used for error detection or

error correction. When they are used for error detec-

tion, a request for retransmission (called automatic

repeat request (ARQ)) is fed back to the transmitter.

When they are used for error correction (calledfomard

error correction

(FEC)),

the link operates without

interruption, and the error control is transparent to other

levels of the system. Forward error correction can

operate with noisy links and low transmitted power,

whereas ARQ cannot; ARQ will play a reduced role in

future systems.

English-language textbooks on error-control codes

include Berlekamp (reference

8),

Blahut (reference

9),

Clark and Cain (reference lo), Lin and Costello (refer-

ence 1 l), and Peterson and Weldon (reference 12).

\

CHANNEL

/

CROSSOVER PROBABILITY

Fig.

15.

Capacity

of

binary

symmetric

and

binary

erasure

channels.

INFORMATlW THEORY AND CODING

25-15

Block

Codes

An

(n,

k)

block code for error control encodes a block

of

k

information symbols into a block of

n

codeword

symbols. Each symbol is an m-bit byte. The rate,

R,

of

the code is equal to

kln.

The rules for constructing good block codes for error

control make use of the arithmetic of Galois fields. A

Galois field with 2m elements, denoted GF(2m), is an

arithmetic system containing the operations of addition,

subtraction, multiplication, and division defined in such

a way that most arithmetic and algebraic procedures are

valid. The arithmetic operations themselves are uncon-

ventional but have the enormous advantage that there is

no overflow nor round-off error. Since the error control

code is used to process bit packages but not to do real

computations, it does not matter that the arithmetic

rules are unconventional. Chart

1

shows addition and

multiplication tables for several simple Galois fields.

Notice that GF(2) and GF(3) are modulo 2 and modulo

3 arithmetic, respectively, but GF(4) is

not

modulo 4

arithmetic. Modulo 4 arithmetic cannot form a field

because 2

~ 1

=

2

.

3(mod 4),

so

division by

2

does not

behave properly. Large fields such as GF(2.56) are very

important in practice, but the multiplication tables are

too large to show here.

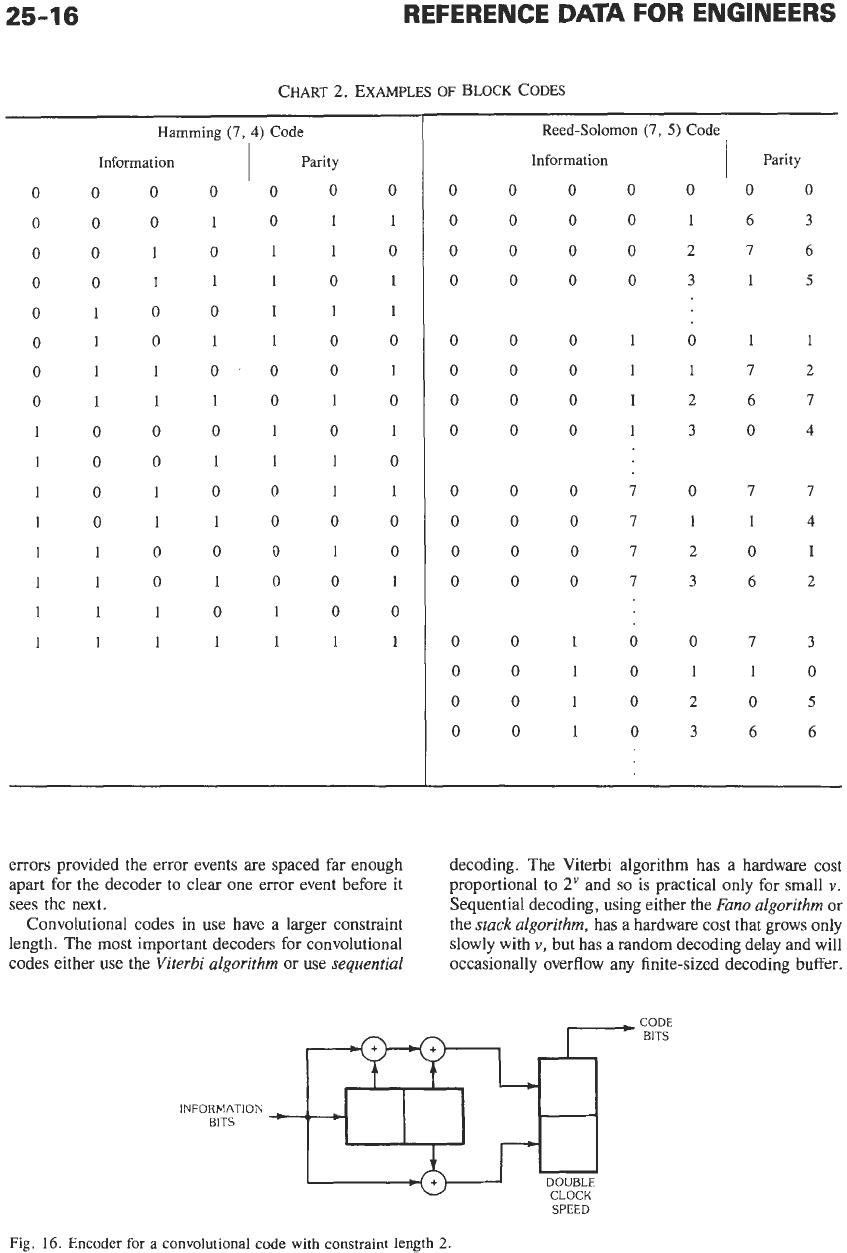
Chart 2 shows the set of codewords of the Hamming

(7,

4) code, a binary code-symbols in GF(2)-that

can correct a single bit error. This simple code has

sixteen codewords.

Chart 2 also shows some of the

codewords of the Reed-Solomon

(7,

5)

code, an octal

code-symbols are in GF(8)-that can correct a single

octal symbol in error. This code has 8’, or 32 768,

codewords. This second example is actually a very

small code although the number of codewords is already

CHART 1. EXAMPLES

OF

FINITE FIELDS

GF(2)

~*

*

GF(3)

*

2201

2021

y;

.~0123

00000

1032 10123

2301 20231

3210 30312

too great to enumerate. This is why it is important

to

use the computational structure of a Galois field to

construct the encoders and decoders.

Reed-Solomon

codes as large as a (256 224) code over GF(28) are now

quite practical. This code consists of 224 information

symbols followed by 32 parity symbols and can correct

16 symbol errors; a symbol error is a symbol that is

wrong in any possible way. A symbol in GF(2*) may be

used to represent eight bits by the user, yet on the

channel may be represented by a 256-ary symbol.

The most important block codes in practice are those

known as the

BCH codes

and the

Reed-Solomon codes.

They are important because efficient decoding algo-

rithms exist for them. These decoders are based either

on the

Berlekamp-Massey algorithm

or on the

Euclidean

algorithm,

and they have a hardware cost proportional

to

nt

where

n

is the blocklength and

t

is the number of

errors to be corrected.

Convolutional Codes

A convolutional code encodes a stream of informa-

tion symbols into a stream of codeword symbols. The

duration of the stream is

so

long that it is effectively

infinite and does not enter into the design of the encoder

and decoder. An information sequence is shifted into

the encoder beginning at time zero and continuing

indefinitely into the future. The stream of incoming

information symbols is broken into segments

of

k,

symbols called information frames, which often may be

as short

as

one symbol in practice. The encoder can

store

m

frames. During each frame time, a new

information frame is shifted into the encoder, and the

oldest information frame is shifted out and discarded.

At the end of any frame time, the encoder has stored the

most recent

m

frames, a total of

mk,

information

symbols. At the beginning of a frame, from the new

incoming information frame and the

rn

previously

stored information frames, the encoder computes a

single codeword frame of length

no

symbols. This

codeword frame is shifted out of the encoder as the next

information frame is shifted in. Hence, the channel

must transmit

no

codeword symbols for each

ko

infor-

mation symbols. The rate,

R,

of the convolutional code

is defined as

R

=

ko/no.

The

constraint length,

v,

of a convolutional code is

defined as the number of memory stages in a minimum

encoder. The complexity of a decoder is often

4’.

Binary convolutional codes used in practice may have a

constraint length in the range

of

about seven

to

forty.

Fig. 16 shows an encoder for a much simpler convolu-

tional code, one of constraint length 2 with

ko

=

1

and

no

=

2. A trellis description of the code is shown in Fig.

17.

The convolutional code

is

the set of all semi-infinite

binary words that may be read off any path through the

trellis. A “zero” information bit entering the encoder at

any node is encoded into the upward path out of that

node, and a “one” information bit is encoded into the

lower path. This convolutional code is able to correct

any number of error events each containing two bit

25-16

REFERENCE

DATA

FOR ENGINEERS

CHART

2.

EXAMPLES

OF

BLOCK

CODES

Hamming

(7,

4)

Code

Information Parity

0

0 0

0

1

0

1 1

0

1

0

1

0

I

0

1

0

1

0

1

0

1

0

1

0

1

0

1

0’

0

1

0

1

1 1

0

1

0

1

0

0 0

1

0

1

0

1

0

1

0

1

0

1

0

1

0 0 0

1

0

1

0

1

0

1

0

1

0

1

0 0

1 1

1

1 1

1

Reed-Solomon

(7,

5)

Code

Information Parity

0

0 0

0

1

6

3

0

0 0

2

7

6

0

3

1

5

0

1

0

1

0 0

0

1

7

2

0 0 0

1

2

6

7

0 0

0

1

3

0

4

0

7

0

7

0

7

1

4

0 0

0

7

2

0

1

0

7

3

6

2

0

1

0 0

7

3

0

1

0

1 1

0

1

0

2

0

5

0

1

0

3

6

errors provided the error events are spaced far enough

apart for the decoder

to

clear one error event before it

sees the next.

Convolutional codes in use have

a

larger constraint

length. The

most

important decoders for convolutional

codes either use the

Viterbi algorithm

or

use

sequential

decoding. The Viterbi algorithm has a hardware cost

proportional to

2”

and

so

is practical only for small

v.

Sequential decoding, using either the

Fano algorithm

or

the

stack algorithm,

has a hardware cost that grows only

slowly with

v,

but has a random decoding delay and will

occasionally overflow any finite-sized decoding buffer.

CLOCK

SPEED

Fig.

16.

Encoder

for

a

convolutional code

with

constraint

length

2.

INFORMATION THEORY AND CODING

25-17

State

00

10

01

11

t

MOST

RECENT

INPUT

Fig.

17.

Trellis diagram

for

a

convolutional code

with

constraint length

2.

CONTINUOUS CHANNELS

AND SOURCES

A discrete information source generates information

at a finite rate; the entropy rate, which measures the

information generated, is finite. A continuous informa-

tion source can assume any one of an infinite number of

amplitude values and

so

requires an infinite number of

binary digits for its exact specification. The entropy rate

is infinite. An immediate consequence of this is that in

order to transmit the output of a continuous information

source and recover it exactly, a channel of infinite

capacity is required. Since, in practice, every continu-

ous channel is perturbed by noise and therefore has a

finite capacity, it is not possible to transmit the output

of a continuous source over a channel and recover it

exactly; there is always some distortion.

We distinguish among a discrete source or channel, a

continuous source or channel defined on discrete time

instants, and a waveform source or channel defined on a

continuum of time points.

A waveform channel can be made into a discrete

channel by choosing a finite set of modulation wave-

forms for the channel. The relationship between wave-

form design and information theory

is

discussed in

Wozencraft and Jacobs.* A waveform source can be

made into a continuous source by sampling, provided

the bandwidth

is

finite, and into a discrete source by

sampling and quantization provided a small amount

of

distortion can be introduced.

The Sampling Theorem

The sampling theorem is an important aid in the

design and analysis of communication systems involv-

ing the use of continuous time functions

of

finite

*

Reference 13.

bandwidth. The theorem states that, if a function of

time,f(t), contains no frequencies of

W

hertz or higher,

then it is completely determined by giving the value of

the function at a series of points spaced

(2W)-'

seconds

apart. The sampling rate of

2W

samples per second is

called the

Nyquist

rate.

If

f(t)

contains no frequencies of

W

hertz or higher,

then it can be recovered from its samples by the

Nyquist-Shannon interpolation formula:

+so

f(t)

=

f(n/2~)

{[sin

.~(2~t-n)l/.~(2~t-n)}

The sampling theorem makes no mention of the time

origin of the samples; it is only the spacing of the

samples that matters.

If function

f(t)

is negligible in magnitude outside a

time interval

T

and has negligible energy at frequencies

higher than

W

hertz, it can be specified by

2TW

ordinates. If a Gaussian noise process with rectangular

spectrum is sampled at the Nyquist rate, the samples are

independent.

n=

-x

Differential Entropy

The differential entropy of a continuous random

variable,

X,

with probability density function

p(x)

is

defined as

H(X)

=

-!+m

-00

p(x)

logfl(x)dx

The differential entropy is

not

the limiting case

of

the

entropy; the entropy of a continuous distribution is

infinite. The differential entropy is not invariant under

coordinate transformations. By itself, it has no funda-

mental physical meaning, but it occurs often enough to

have a name.

Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications

Подождите немного. Документ загружается.