Middleton W.M. (ed.) Reference Data for Engineers: Radio, Electronics, Computer and Communications
Подождите немного. Документ загружается.


24-16
REFERENCE
DATA
FOR ENGINEERS
Fig.
11.
Matched filter receiver.
h,(f)
=
sd(T0
-
t)
The statistic
Z(To)
can therefore be expressed as
z(T0)
==
I_”..
Y(T0
-
U)
Sd(T0
-
U)
du
If the signals
so
and
s
I
are time limited to
[O,
TI
and the
sampling time is
To
=
-T,
this expression reduces to
Z(T)
=
Y(t)
sd(t)
dt
c
Thus,
Z(T)
can be obtained by multiplying the channel
output
Y(t)
by the signal
s&)
and integrating from
0
to
T,
as shown in Fig.
12.
The receiver that processes the
channel output in this manner is known as the
correla-
tion
receiver.
The correlation receiver gives the same
error probability as the matched-filter receiver.
Coherent Receivers for Binary
and Quaternary RF Signals
For binary RF communications with signals of the
form
s(t)
=
.\/z
s&)
cos[25Q
+
91
the matched-filter receiver for an additive white Gaussi-
an noise channel is the receiver portion of the system
shown in Fig.
10
with
h(t)
=
/I&).
As
in baseband
systems, the correlation receiver can be substituted for
the matched filter
in
coherent
RF
communication sys-
tems. The correlation receiver for coherent RF commu-
nications is shown in the diagram
of
Fig.
13.
Notice from Fig.
13
that the receiver must know the
carrier phase
9.
In practice, it suffices to have a good
estimate of this phase, and there are many different
kinds of tracking
loops
that can be employed in the
receiver to provide such an estimate.
A
presentation of
phase-tracking loops and related synchronization devic-
es may be found in reference
5.
Binary phase shift keying (BPSK) employs binary RF
signals with
s,(t)
=
A/d
for
0
5
t
<
T
(see subsection
Fig.
12.
Correlation receiver.
on
BPSK). The optimum correlation receiver for coher-
ent reception of BPSK is shown in Fig.
14.
This is a
special case of the receiver of Fig.
13.
The square of the
BPSK signal contains an unmodulated carrier at fre-
quency 2f, and phase
24,
and this double-frequency
carrier can be used to provide an estimate of the phase
Cp
(this is the squaring loop*). This estimate is employed
as the phase reference for coherent demodulation.
An
alternative method for coherent demodulation is to have
the detection filter in the loop such as with a Costas
loop or an
I-Q
loop.*
The coherent receivers for QPSK, OQPSK, and MSK
are of the form shown in Fig. 15. These receivers
consist of two branches, and each branch is a correlation
receiver for an appropriate binary signal. The coherent
references for the two branches differ in phase by
7r/2
radians, and in general there is a timing offset
T‘
between the in-phase and quadrature branches. If the
data rate is
R
=
1/T bits per second in each case, then
T’
=
T
for OQPSK and
MSK,
but
T’
=
0
for QPSK.
The waveform
v(t)
is the rectangular pulse
pzT(t)
for
QPSK and OQPSK, and it is the sine pulse
sin
(at/2T)
pZT(t)
for MSK.
Noncoherent Receivers
The signals employed
in
noncoherent communica-
tions are binary and M-ary signals of the type described
in the subsections
on
FSK and MFSK. The signal set
consists of
M
equal-energy signals of the form
where
a&)
and
e,(?)
are baseband signals with band-
widths much smaller than the carrier frequency
f,.
For noncoherent demodulation, it is assumed that the
receiver has
no
knowledge of the phase
+k
and that the
phases for different signals are unrelated (e.g.,
&
and
+j
are statistically independent for
k
#
j).
Moreover,
for some applications,
a
time-varying phase shift is
introduced by the channel,
so
the phase of the received
signal may change from one interval to the next.
-
*
Reference
5.
DEVICE
&Sd(l)
COS
IZT!,t+o]
Fig.
13.
Coherent
correlation
receiver
for
RF
signals.
A
cos
IZrf~-o]
Fig.
14.
Coherent
correlation
receiver
for
BPSK.

COMMUNICATIONS
24-
17
THRESHOLD
DEVICE
-
THRESHOLD
DEVlCE
Fig.
15.
Coherent receiver
for
quaternary RF signals.
The key component of the 'optimum noncoherent
receiver for the signal set given above and an additive
white Gaussian noise channel is the noncoherent
corre-
lation detector
(NCD),
which is
also
referred to as
an
envelope correlation detector.
*
A block diagram of the
noncoherent correlation detector for the signal
sk(t)
is
shown in Fig. 16. This detector consists of in-phase and
quadrature correlation receivers followed by squaring
devices and
a
summing device. Thus the output of the
noncoherent correlation detector is the square-law com-
bination of the outputs of two correlation receivers
whose phase references differ by ?rl2 radians. For
convenience, let
NCDIk
denote the noncoherent corre-
lation detector for the kth signal in the set.
Let
Pe,k
denote the probability that an error is made
by the receiver when the signal sk(t) is sent. Two
performance measures of interest are the maximum
probability of error
P,,,
=
max{P&
=
0,
1,
.
.
.
,
M
-
1)
and the average probability of error
pe,~
=
Pe,oPo
+
~~,IPI
+
. . .
+
Pe,M- IPM-
1
In the expression for the average probability of error,
Pk
denotes the a priori probability that the signal sk(t) is
sent. The receiver that gives the minimum possible
*
Reference
10.
value of
P,,,
also gives the minimum possible value of
Pe,A
for equally probable signals (i.e.,
pk
=
1IM
for
each
k).
The block diagram for this optimum receiver is
shown in Fig. 17. The decision of the receiver is based
on a comparison of the outputs of the noncoherent
correlation detectors: the receiver decides the ith signal
was sent if
Z,
=
max{Zk:k
=
0,
1,
.
.
.
,
M
-
I}
If the signals have unequal a priori probabilities,
some additional processing of the outputs of the nonco-
herent correlation detectors is necessary in order to give
the minimum average probability of error.
*
This
is
also
necessary for signals with unequal energy.
Since MFSK is
a
special case of M-ary signaling, an
optimum receiver for MFSK can be obtained from Figs.
16
and 17. The signals for MFSK are
~k(t)
=
A
~0~[24t
+
4k]
so
the noncoherent correlation detector for MFSK uses
reference signals c0s(2rjkt) and sin(2rrfkt) as shown in
Fig.
18.
An optimum noncoherent receiver for MFSK is
obtained by employing this noncoherent correlation
detector in the system of Fig. 17. An optimum non-
coherent receiver for binary FSK is this system with
M
=
2.
*
Reference
10.
SQUARING
DEVICE
*
Fig.
16.
Noncoherent correlation detector
(NCDIR).

24-
18
REFERENCE DATA FOR ENGINEERS
NCD/O
rcltl
Fig.
17.
Diagram
of
noncoherent
receiver
for
M-ary
commu-
nications.
If the channel noise is a band-limited white Gaussian
noise process and the noise bandwidth is small com-
pared to the tone frequencies
fk,
there is an alternative
implementation of the optimum noncoherent receiver
that utilizes an
envelope detector.
In order to describe
the response
of
the envelope detector to narrow-band
inputs, define the signal
xk(t)
=
v(t)
COS(^$^^)
+
w(t)
sin(2n@)
since no phase information is utilized in
hk(t).
The
output of the system of Fig.
19
at time Tis equivalent to
the output
of
the noncoherent correlation detector. Thus
the matched filterlenvelope detector can be substituted
for the noncoherent correlation detector in the system of
Fig. 17 to obtain an alternative form of the optimum
receiver.
ERROR PROBABILITIES FOR
DIGITAL COMMUNICATION
SYSTEMS
In the preceding section, the optimal receivers are
given for the most commonly used digital modulation
techniques. Although there are a large number of
different modulation techniques, many of them give the
same performance. Throughout this section, perform-
ance will be measured by the
bit error probability
Pb
as
a
function of the
bit energy to noise density ratio
E,/&.
Issues such as bandwidth and complexity of implemen-
tation will not be considered (see the subsection titled
“Spectra of
PSK
and MSK Signals” for some com-
ments on bandwidth of
PSK
and MSK signals).
Most binary communication systems of practical
interest fall into two categories: coherent detection bf
antipodal signals and noncoherent detection
of
orthogo-
nal signals. Moreover, certain quaternary signal
sets
such as QPSK, OQPSK, and MSK have the same bit
error probability as binary antipodal signaling. For
M-ary modulation, the primary case of interest is
orthogonal signaling with noncoherent demodulation.
in terms
of
baseband signals
v(t)
and
w(t)
that are
narrow-band with respect to the frequencyfk.
If
nk(t)
is
the input to an envelope detector, the output is
e(t)
=
[v2(t)
+
w2(t)1
”*
The signal
e(t)
is
called the
envelope
of
the narrow-band
signal
xk(t).
Let
hk(t)
he the impulse response of a filter matched
to the kth tone
of
the MFSK signal set; that is, let
hk(t)
=
COS
(2n3P,t)
In contrast to the matched filters of the preceding
subsection, this filter is
noncoherently matched
to the
signal
Sk(t)
=
A
~0~[2.rrfkt
+
$k]
Coherent Systems
With
Additive White Gaussian Noise
Channels
As
discussed in the subsection titled “Receivers for
Binary Baseband Data Transmission,” binary coherent
RF communication systems can be analyzed in terms of
their low-pass equivalent systems. Thus, the results of
that subsection give the error probabilities for optimum
coherent demodulation
of
binary RF signaling over
additive white Gaussian noise channels. If the channel
noise has spectral density N012, the error probability for
.
SQUARING
DEVICE
--
‘
SQUARING
DEVICE
sin
(2irfkt)
Fig.
18.
Noncoherent
correlation
detector
(NCD/k)
for
MFSK
signal
set.

DIGITAL COMMUNICATIONS
24-19
MATCHED
FILTER
Fig.
19.
Noncoherent matched filter/envelope detector.
binary signaling (baseband or
RF)
with an optimum
receiver is
Pb
=
Q{[EA(l
-
r)/No]1’2}
where,
r
is the correlation coefficient for the binary
EA
is the average of the energies
Eo
and
E,
for
signal set,
the two signals (see subsection cited above for
formal definitions).
The binary signal sets of greatest interest are the
anti-
podal (r
=
-1)
and
orthogonal (r
=
0)
equal-energy
signals. If the two signals have equal energy,
EA
=
Eo
=
E
I
,
and
thus
the
energy per bit
is
EA
regardless of
which bit is transmitted. For equal energy signals
(binary or M-ary), it is customary to specify the
performance in terms of the energy per bit, which is
denoted by E,.
It follows from the above comments that the bit error
probability for optimum coherent detection of binary
antipodal signals is
For most applications, it is convenient to give the bit
energy to noise density ratio in decibels. For this
purpose, we define
A
graph of
Pb
versus (Eb/&)dB for optimum demodula-
tion and antipodal signaling is given in Fig.
20.
Note
that since binary PSK is just a special case of antipodal
signaling, this curve applies to coherent detection of
BPSK. Coherent detection of binary
ASK
with antipo-
dal signals is another special case.
Many of the quaternary communication systems have
the same bit error probability as binary antipodal
signaling with an optimum receiver. The bit error
probability
for
optimum coherent demodulation
of
QPSK, OQPSK, or MSK is given by
exactly the same as for optimum coherent demodulation
of BPSK. Consequently, the performance curve for
QPSK, OQPSK, and MSK
is
the curve in Fig. 20 that
corresponds to binary antipodal signaling.
arises
so
frequently in the analysis of the performance of
Because the error probability
Q[(2Eb/No)
coherent communication systems, a short table of its
values is given in Table
1.
The table lists
(E
/NO)dB,
If the phase reference
is
not perfect, such as when it
is estimated by some kind of tracking loop, the error
probability for BPSK and related modulation schemes
will be larger than given above. The
phase error
(6,
is
the difference between the reference phase and the
phase of the received signal. If
(6,
is constant for the
duration of the data bit, the bit error probability for
BPSK is
Eb/No, and the error probability Q[(2Eb/&)”
!
1.
Pb
=
Q[(2Eb/No)”’ cOS((6,)l
Coherent receivers for M-ary orthogonal signaling are
of limited interest in applications. This is primarily
because of the relative inefficiency of orthogonal signal-
ing in a coherent system. For example, binary FSK
requires twice the signal energy of BPSK to give the
same bit error probability in a coherent system. This is
true of any binary orthogonal signal set, since
r
=
0
implies
Pb
=
NO)^'*]
If a coherent receiver is to be employed, it makes sense
to use a modulation scheme that is more efficient than
orthogonal signaling.
The error probabilities for coherent demodulation of
M-ary orthogonal signals are given in reference
5.
The
error probabilities for noncoherent demodulation of
M-ary orthogonal signals are given in the next subsec-
tion. For large values of M, the performance of the
coherent system
is
not much better than the perform-
ance of the noncoherent system (especially for low error
probabilities). This is another reason there is little
interest in implementing the more complex coherent
receiver if M-ary orthogonal modulation is employed.
For further discussion of this and related topics see
reference
5.
Noncoherent Systems With
Additive White Gaussian Noise
Channels
The performance curve for binary FSK can be
obtained by considering binary, orthogonal, equal-
energy signals. For such signals, the bit error probabili-
ty
for
optimum noncoherent detection is
Pb
=
0.5
exp(-Eb/2No)
which is also shown in Fig. 20.
Closely related to binary orthogonal signaling, al-
though not always viewed as such, is
differential phase-
shift keying
(DPSK). In DPSK, binary digits are trans-
mitted at a rate of
1/T
bits per second by phase
transitions at the ends of successive T-second intervals.
A
phase change of
180
degrees can represent a binary
1,
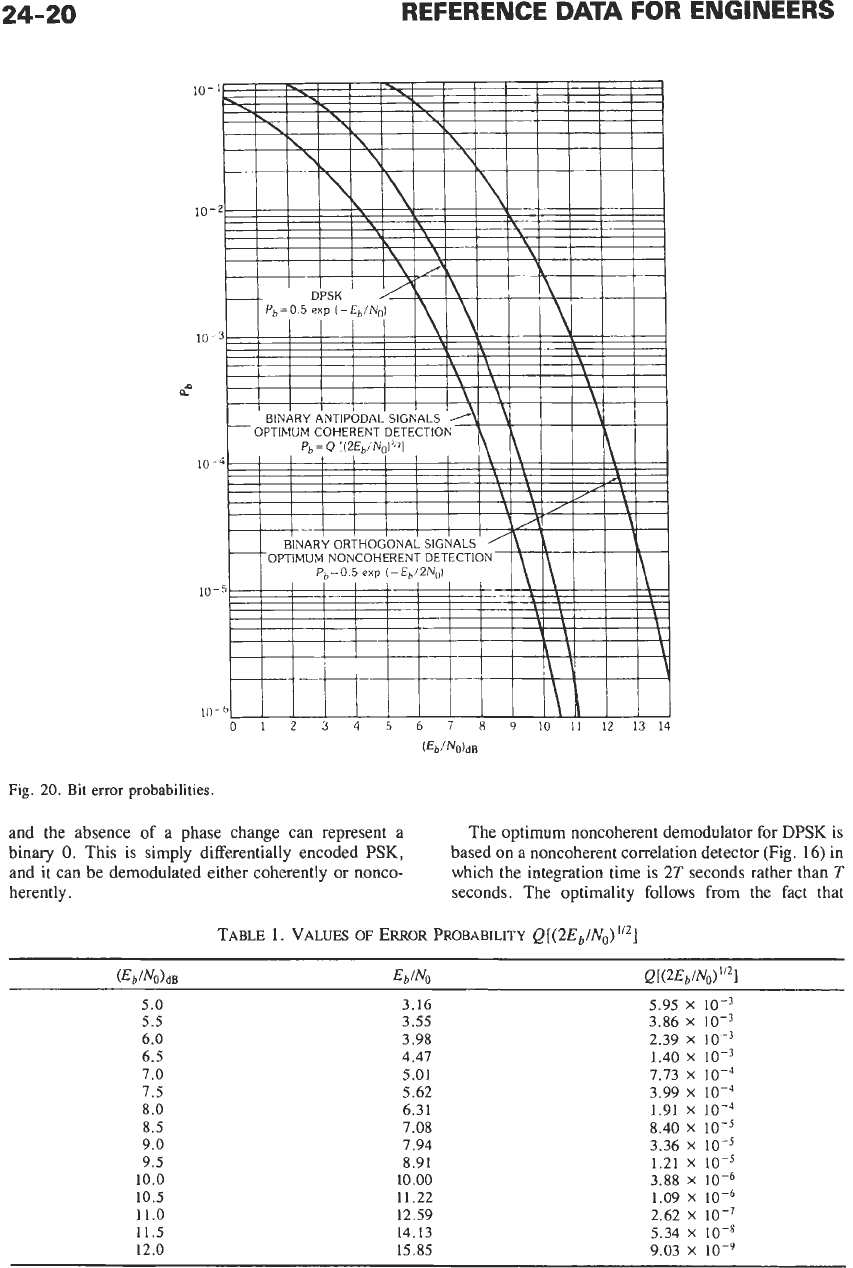
24-20
REFERENCE
DATA
FOR ENGINEERS
10-1
Iihl\l1\1
I
I
I
I
\I
I\I
I
I\l
I I
I
I
1
1
.o-4
I\
I\
I
I I\ I
OPTIMUM NONCOHERENT DETECTION
I
1
pb
=
o
5
exp
i
-
E,/ZN,,I
Fig.
20.
Bit
error
probabilities.
and the absence
of
a phase change can represent a
binary
0.
This is simply differentially encoded
PSK,
and it can be demodulated either coherently or nonco-
herently
.
The optimum noncoherent demodulator
for
DPSK
is
based on a noncoherent correlation detector (Fig.
16)
in
which the integration time is
2T
seconds rather than
T
seconds. The optimality follows from the fact that
TABLE
1.
VALUEs
OF
ERROR
PROBABILITY
&[(2E,/N,)
'''1
5.0
5.5
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
11.0
11.5
12.0
3.16
3.55
3.98
4.47
5.01
5.62
6.31
7.08
7.94
8.91
10.00
11.22
12.59
14.13
15.85
5.95
x
10-3
3.86
x
10-3
2.39
x
10-3
1.40
x
10-3
7.73
x
10-4
3.99
x
10-~
1.91
x
10-4
8.40
x
10-5
3.36
x
10-5
1.21
x
10-5
2.62
x
10-7
5.34
x
10-8
9.03
x
10-9
3.88
X
1.09
X
DIGITAL COMMUNICATIONS
24-21
DPSK is a form of orthogonal signaling on the interval
[0,2T]:
the signal corresponding to a 180-degree phase
change is orthogonal to the signal corresponding to no
phase change. Since the integration time is
2T,
the
effective signal energy is
2Eb.
For optimum nonco-
herent demodulation of orthogonal signals of energy
2Eb,
the error probability is
Pb
=
0.5
eXp
(-Eb/No)
which is shown in Fig.
20.
The noncoherent correlation detector structure can be
simplified to provide the alternative implementation of
the optimal noncoherent demodulator for DPSK that is
shown in Fig.
21.
For this receiver the decision is made
as follows. If
w,z,
+
w,z,
>
0
the decision is that
0
was sent, and if
w,z,
+
w,z,
<
0
the decision is that
1
was sent.*
A suboptimal receiver that is commonly suggested
for demodulation of DPSK involves delay and multipli-
cation of the received continuous-time signal, as shown
in Fig.
22.
The delay-and-multiply receiver does not
produce the same decision statistic as the receiver
shown in Fig.
21,
and its probability of error is larger
than that obtained by the receiver of Fig.
21.
For very
large values of the signal-to-noise ratio, the perform-
ance difference between the two receivers is small.
*
See reference
7
for
details.
Additional information on DPSK reception is given in
references
6,
7,
and
8.
Next we consider
M-ary
signaling with equal-
energy, orthogonal signals. That is, the signal set
{sk:k
=
0,
1,
.
.
.
,
M
-
1)
is
such that
llsk1I2
=
E,
for
all
k,
and
(sk,
sj)
=
0
whenever
k
#
j.
The energy in the
signal
sk
is called the
energy
per
symbol
(denoted by
E,).
A symbol error occurs if the receiver decides that
si
was sent when in fact
sk
was sent and
k
#
j.
For an
additive white Gaussian noise channel and an optimum
noncoherent receiver, the symbol error probability
P,
is
given by
M
P,
=
M-'
(
M)(-l)n
exp{-[(n
-
l)/n]E,/No}
n=2
This can be evaluated on a digital computer for values of
M
up to
32,
although double precision computation may
be required for values of
M
larger than about
16.
The
symbol error probability can be computed for larger
values of
M
by numerical integration of an alternative
expression for
P,;
for example, see equation (10-15) on
p. 489 of reference
5.
If
Mary
modulation is employed to transmit binary
data,
M
should be
a
power of
2.
If
M
=
2m,
each
M-ary
symbol can represent a unique sequence of
m
binary
digits. The energy per bit is
Eb
=
E,/m.
A
symbol error
can cause as few as one or as many
as
m
bit errors. On
the average, the number of bit errors per symbol error is
mM/2(M
-
1)
for M-ary orthogonal signaling with
optimum noncoherent demodulation. Thus the bit error
probability
Pb
is related to the symbol error probability
by
Pb
=
MPs/2(M
-
1).
Making the appropriate
substitutions in the above expression for
Ps,
we find that
the bit error probability is given in terms of the energy
per bit by
Fig.
THRESHOLD
21.
Optimal noncoherent demodulator for
DPSK.

24-22
(EblNO)dB
THRESHOLD
@--j-t+f-t+
DEVICE
y(f'(
t
Fig.
22.
The
delay-and-multiply
receiver-a
suboptimal
receiver
for
DPSK.
Symbol
Error
Probability,
P,
M=2 M=8
M
=
32
A
table of values of the symbol error probability is
given in Table 2 for
M
=
2,
8,
and 32. The bit error
probabilities can be obtained from this table by multi-
plying the symbol error probabilities by M/2(M
-
1).
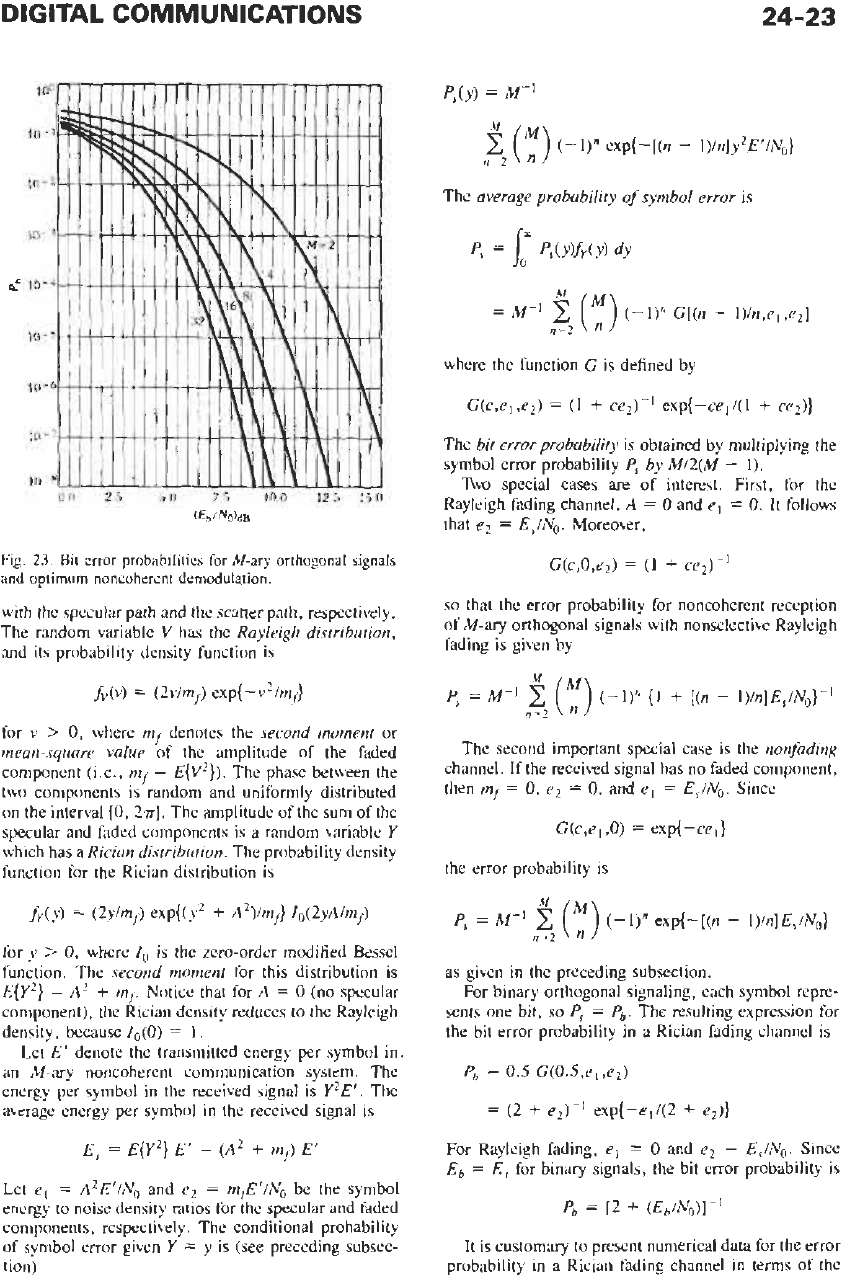
Curves of the bit error probability versus the bit energy
to noise density ratio are shown in Fig. 23 for
M
=
2,4,
8,
16, and 32. It can be shown that
Pb
-+
0
as
M
+=
m
provided that Eb/No is greater than In 2 (where In
denotes the natural logarithm).
3.0
4.0
5.0
6.0
7.0
8.0
9.0
10.0
Noncoherent Systems With
Nonselective Fading Channels
1.84
X
lo-'
1.05
X
IO-'
5.03
X
lo-'
1.42
X
lo-' 5.38
X
lo-? 1.71
X
1.03
X
lo-'
2.25
X
4.03
x
10-3
6.83
X
lo-? 7.25
x
10-3 6.03
x
10-4
4.08
X
lo-?
1.67
x
10-3 5.08
x
10-~
2.13
X
2.53
x
10-4 2.10
x
10-6
9.42
x
10-3 2.21
x
10-5 3.64
X
lo-*
3.37
x
10-3 1.06
X
2.15
X
10-l'
In some communication channels, there are several
propagation paths between the transmitter and the
receiver. The signal components arriving at the receiver
from different paths add destructively or constructively
depending on the difference in the propagation times
and on any phase shifts introduced by the medium
(e.g., reflections from objects). Thus the signal strength
depends on the relative phasing of the components of
the received signal, and this gives rise
to
the condition
known as
fading.
If
the differential propagation times for the paths are
small compared with the data symbol duration, and the
path strengths, propagation times, and phase shifts are
nearly constant for the duration of the symbol, then
there is
no
significant dispersion of the signal. In this
case, the fading is referred to as
slow nonselective
fading.
If the differential propagation times are large
compared with the data symbol duration, signal disper-
sion will occur. Such channels are known as
time-
dispersive
or
frequency-selective
fading channels.
These channels may produce significant levels of inter-
symbol interference.
A
more complete discussion of
fading and its effects on communication systems is
given in reference
8,
and the derivations of the results
given in this section can be found in references 12, 13,
and 14.
For
slow nonselective Rician fading,
the received
signal is the sum of a nonfaded version of the transmit-
ted signal and a slow nonselective Rayleigh faded
version. The difference in propagation times for the two
components is small enough that the channel is nonse-
lective. The nonfaded component of the received signal
is called the
specular component,
and the Rayleigh
faded component is sometimes called the
random
or
scatter component.
The specular component may result
from a direct path between the transmitter and receiver,
and the faded component may arise from a large number
of reflections.
Consider the transmission of a unit-amplitude RF
signal over this Rician fading channel. The received
signal is the sum of a deterministic component of
amplitude
A
and a random component of amplitude
V.
The quantities
A
and
V
represent the gains associated
DIGITAL
COMMUNICATIONS
24-23
(€blNO)dB
Fig.
23.
Bit
error
probabilities
for
Mary
orthogonal signals
and
optimum
noncoherent
demodulation,
with the specular path and the scatter path, respectively.
The random variable
V
has the
Rayleigh distribution,
and its probability density function is
for
v
>
0,
where
mf
denotes the
second moment
on
mean-square value
of the amplitude of the faded
component (i.e.,
mf
=
E{V2}).
The phase between the
two components is random and uniformly distributed
on
the interval
[0,
274.
The amplitude of the
sum
of the
specular and faded components is a random variable
Y
which has a
Rician distribution.
The probability density
function for the Rician distribution is
~Y(Y)
=
(2~4)
~xP{(Y*
+
A2Ymf} 1,(2yAlmf)
for
y
>
0,
where
Zo
is the zero-order modified Bessel
function. The
second moment
for this distribution is
E{Y2}
=
A'
+
mf
Notice that for
A
=
0
(no
specular
component), the Rician density reduces to the Rayleigh
density, because
I,(O)
=
1.
Let
E'
denote the transmitted energy per symbol in.
an Mary noncoherent communication system. The
energy per symbol in the received signal is
Y2E'.
The
average energy per symbol in the received signal is
E,
=
E{Y~}
E'
=
(A~
+
mf)
E'
Let
e,
=
A2E'/No
and
e2
=
mfE'/No
be the symbol
energy to noise density ratios for the specular and faded
components, respectively. The conditional probability
of symbol error given
Y
=
y
is (see preceding subsec-
tion)
$
(
y)
(-1)''
exp{-[(n
-
I)/n]y2E'/No}
n=2
The
average probability
of
symbol error
is
P,
=
1
PS(Y)fY(Y)
dY
where the function
C
is defined by
G(c,el,e2)
=
(I
+
ce2)-'
exp{-ce,/(l
+
ce2)}
The
bit error probability
is obtained by multiplying the
symbol error probability
P,
by
M/2(M
-
1).
Two
special cases are of interest. First, for the
Rayleigh fading channel,
A
=
0
and
el
=
0.
It follows
that
e2
=
EJN,.
Moreover,
G(c,0,e2)
=
(I
+
ce2)-l
so
that the error probability for noncoherent reception
of
M-ary
orthogonal signals with nonselective Rayleigh
fading is given by
The second important special case is the
nonfading
channel. If the received signal has
no
faded component,
then
mf
=
0,
e2
=
0,
and
el
=
E,/No.
Since
C(c,el
,0)
=
exp{-cel}
the error probability is
P,
=
M-'
5
(:)
exp{-[(n
-
l)/n]E,/No}
n=2
as given in the preceding subsection.
For binary orthogonal signaling, each symbol repre-
sents one bit,
so
P,
=
P'.
The resulting expression for
the bit error probability in a Rician fading channel is
Pb
=
0.5
G(0.5,e,
,e2)
=
(2
+
e,)-'
exp{-el/(2
+
e,)}
For Rayleigh fading,
el
=
0
and
e2
=
EJN,.
Since
Eb
=
E,
for binary signals, the bit error probability
is
Pb
=
[2
f
(Eb/N(()]-'
It is customary to present numerical data for the error
probability in a Rician fading channel in terms of the
24-24
REFERENCE DATA FOR ENGINEERS
ratio of the power
in
the two components of the received
signal. Let
g2
=
mf/A2,
so
that
e2
=
g2
e,.
The
signal-to-noise ratios
el
and
e2
are related to
EJN,
by
e,
=
[I/(
and
e2
=
g2
el
=
The Rician channel
CL
g2/(1
+
g2)1
E,/&
be specified by giving either
e,
and
e2
or
g2
and
EJN,.
In the latter specification,
E,/No
is
a measure of the average signal-to-noise ratio at
the receiver, and
g2
specifies how the signal power is
distributed between its two components. Specifically,
1/(l
+
g2)
is the fraction due to the specular compo-
nent, and
g2/(1
+
g2)
is the fraction due to the faded
component. A substitution for el and
e2
in the expres-
sions above gives expressions for the error probability in
terms of
g2
and
E,/No.
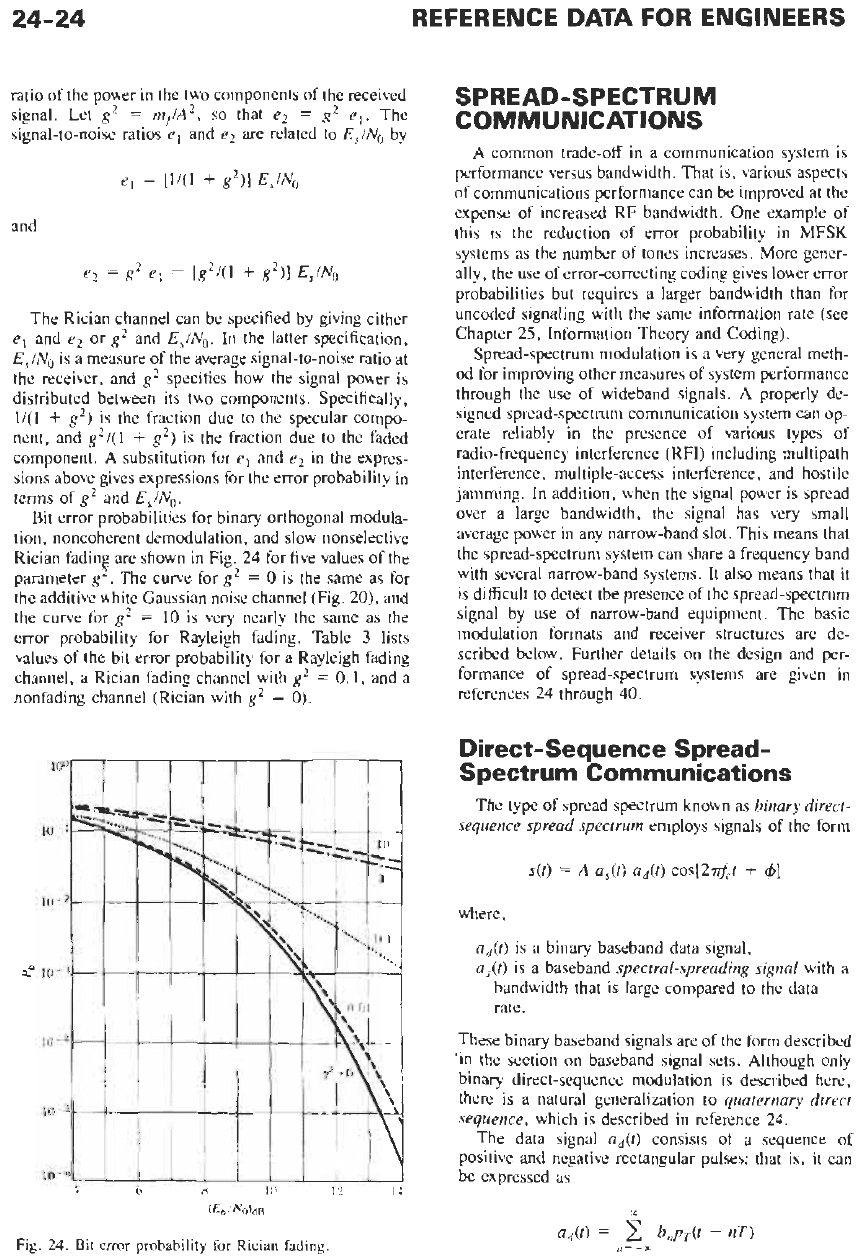
Bit error probabilities for binary orthogonal modula-
tion, noncoherent demodulation, and slow nonselective
Rician fading are shown in Fig. 24 for five values of the
parameter
g2.
The curve for
g2
=
0
is the same as for
the additive white Gaussian noise channel
(Fig.
20),
and
the curve for
g2
=
10
is very nearly the same as the
error probability for Rayleigh fading. Table
3
lists
values of the bit error probability for a Rayleigh fading
channel, a Rician fading channel with
g2
=
0.1,
and a
nonfading channel (Rician with
g2
=
0).
100
10-1
10-2
h
10-3
10-4
10-5
10-0
4
6
X
10
12 14
(Eb
!NO)dB
Fig.
24.
Bit
error
probability for Rician fading
SPREAD-SPECTRUM
COMMUNICATIONS
A common trade-off in a communication system is
performance versus bandwidth. That is, various aspects
of communications performance can be improved at the
expense of increased RF bandwidth. One example of
this is the reduction
of
error probability in MFSK
systems as the number of tones increases. More gener-
ally, the use of error-correcting coding gives lower error
probabilities but requires a larger bandwidth than for
uncoded signaling with the same information rate (see
Chapter
25,
Information Theory and Coding).
Spread-spectrum modulation is a very general meth-
od for improving other measures of system performance
through the use of wideband signals.
A
properly de-
signed spread-spectrum communication system can op-
erate reliably in the presence of various types of
radio-frequency interference (RFI) including multipath
interference, multiple-access interference, and hostile
jamming. In addition, when the signal power is spread
over a large bandwidth, the signal has very small
average power in any narrow-band slot. This means that
the spread-spectrum system can share a frequency band
with several narrow-band systems. It also means that it
is difficult to detect the presence of the spread-spectrum
signal by use of narrow-band equipment. The basic
modulation formats and receiver structures are de-
scribed below. Further details on the design and per-
formance of spread-spectrum systems are given in
references
24
through 40.
Direct-Sequence Spread-
Spectrum Communications
The type of spread spectrum known as
binary direct-
sequence spread spectrum
employs signals of the form
where,
a&)
is a binary baseband data signal,
a,(t)
is a baseband
spectral-spreading signal
with a
bandwidth that is large compared to the data
rate.
These binary baseband signals are of the form described
'in the section on baseband signal sets. Although only
binary direct-sequence modulation is described here,
there is a natural generalization to
quaternary direct
sequence,
which is described in reference 24.
The data signal
a&)
consists of a sequence
of
positive and negative rectangular pulses; that is, it can
be expressed
as

24-25
(Eb/Ntl)dB
4.0
6.0
8.0
10.0
12.0
20.0
14.0
TABLE
3.
BIT
ERROR
PROBABILITIES FOR
BINARY
ORTHOGONAL SIGNALING,
SLOW
NONSELECTIVE
FADING,
AND
NONCOHERENT
DEMODULATION
Bit
Error
Probability
Rayleigh
g2
=
0.1
No
Fading
2.22
x
lo-’ 1.61
X
IO-’
1.42
X
lo-’
1.67
X
lo-’ 9.15
X
lo-’ 6.83
X
lo-’
1.20
x
10-1
4.18
X
IO-’
2.13
X
lo-’
8.33
X
lo-*
1.51
x
10-2
3.37
x
10-~
5.60
X
4.41
x
10-3 1.81
x
10-4
9.80
x
10-3 2.48
x
10-5 9.64
x
10-23
3.69
X
1.13
x
1.76
X
5-.
where,
pr(t)
is the rectangular pulse duration
T,
b,
is either
+
1
or
-
1,
depending on the data bit
Similarly, the spectral-spreading signal can be writ-
to be sent in the nth interval.
ten as
THRESHOLD
DEVICE
-
where
v(t)
is
the
chip
waveform,
a time-limited pulse of
duration
T,.
The parameter
T,
is called the
chip
dura-
tion,
and the sequence
(aj)
=
.
.
.
,
a_,,
a,,,
a,, a2;
-
*
is called the
signature
sequence.
For reasonable choices
of signature sequence and chip waveform,
UT,
is a
rough estimate of the bandwidth of the spread-spectrum
signal. For most direct-sequence systems,
<<
T,
so
the bandwidth of the spread-spectrum signal is much
larger than that of the data signal.
Usually, the data pulse duration
T
is an integer
multiple of the chip duration. If
T
=
NT,
for some
integer
N,
there are
N
chips per data pulse, and the
bandwidth of the spread-spectrum signal is roughly
N
times the data rate. Usually the signature sequence is
periodic, and the period
p
is equal to
N
or elsep
>>
N,
depending on the nature of the application.
The optimum receiver for binary direct-sequence
spread-spectrum modulation and an additive white
Gaussian noise channel (Le., thermal noise is the only
interference)
is
the correlation receiver shown in Fig.
25
(cf. Fig.
14).
The received signal
Y(t)
is multiplied by
A
a,@)
cosP.?rf,t
+
$1
A
OJtI
cos
[2iii,l+dl
Fig.
25.
Coherent
correlation
receiver
for
binary
direct-
sequence spread
spectrum.
and the product is integrated over an appropriate
interval of length
T
(this is illustrated for the interval
[0,
TI
in Fig.
25).
Since the signals corresponding to
b,
=
+1 and
b,
=
-1
are antipodal, the bit error
probability for binary direct-sequence spread-spectrum
modulation and optimum coherent demodulation is
the same as for binary
BPSK
with optimum coherent
demodulation.
The motivation for considering direct-sequence
spread spectrum is not performance improvement for
channels in which the primary interference is thermal
noise. Rather, it
is
the fact that the spectral-spreading
signal can be selected to give the transmitted signal
certain desirable properties and enable the receiver
to
discriminate against forms of interference other than
thermal noise. For example, if the spread-spectrum
signal is corrupted by additive
RFI,
and if we ignore the
thermal noise for the moment, the received signal can
be written as
Y(t)
=
s(t)
+
x(t),
where
x(t)
is an additive
interference signal. The effects of this interference can
be reduced by choosing the spectral-spreading signal to
minimize
One application in which additive RFI is encountered
is in a direct-sequence spread-spectrum
multiple-access
communication system.* In such a system, signals from
the various transmitters have the same carrier frequency
f,.
The spread-spectrum signals from other transmitters
appear as additive RFI to a receiver that attempts to
demodulate the signal
s(t).
Let
s‘(t)
denote one of these
other signals, and denote
its
spectral-spreading signal
by
a‘,@)
and its signature sequence by
(a;).
Since the
signal
s‘(t)
is from a different transmitter than
s(t),
it
arrives at the receiver with a different propagation delay
and phase angle.
If
u
denotes the propagation delay and
__
*
Reference
24.
