Михалевська Т.В., Ісаєнко В.М., Гроза В.А. Основи статистичного обліку і банки інформації в екології. НАУ-друк, 2009

Подождите немного. Документ загружается.

101

Застосування того чи іншого способу формування вибіркової су-

купності залежить від мети вибіркового обстеження, можливостей

його організації і проведення. Найпоширенішими є комбіновані ви-

бірки, які поєднують різні способи відбору: систематичний і серій-

ний, районований і систематичний, простий випадковий і серійний.

Поєднання способів відбору забезпечує високу репрезентативність

результатів з найменшими трудовими і грошовими витратами на

організацію і проведення досліджень.

Середня похибка вибірки при різних комбінаціях її видів і спосо-

бів визначається по-різному.

Залежно від того, як змінюється одиниця відбору, при послідов-

ному проведенні кількох вибірок розрізняють одноступінчастий і

багатоступінчастий відбір одиниць у вибіркову сукупність.

Одноступінчаста вибірка передбачає, що з досліджуваної сукуп-

ності одразу відбираються одиниці або серії одиниць для безпосере-

днього обстеження.

Багатоступінчаста вибірка припускає поступове вилучення із

генеральної сукупності спочатку збільшених груп одиниць, потім

груп, менших за обсягом, допоки відберуть відповідні групи або

окремі одиниці для подальшого дослідження. Вибірка може бути

дво-, триступінчастою і більше. Однак треба уникати великого чис-

ла ступенів, детально плануючи організацію вибіркового спостере-

ження. У багатоступінчастому відборі поєднуються різні способи.

Особливим видом вибіркового спостереження є моментне спо-

стереження, суть якого полягає в тому, що на встановлені моменти

часу фіксують окремі елементи процесу досліджуваного явища. За

допомогою моментного спостереження отримують потрібну інфор-

мацію скоріше та з меншими затратами, ніж при суцільному спосте-

реженні.

КОНТРОЛЬНІ ПИТАННЯ

1. Назвіть види і способи відбору у вибіркову сукупність.

2. Як здійснюють випадковий і механічний відбір?

3. Що таке моментне спостереження?

5.3. Визначення середньої і граничної похибок

Вибіркова сукупність має пізнавальне значення, оскільки дає

уявлення (з певною ймовірністю) про показники генеральної сукуп-

ності. Але, як уже зазначалося, при вибірковому спостереженні мо-

жуть виникати помилки спостереження. У разі несуцільного спосте-

102

реження, зокрема вибіркового, крім помилок реєстрації можливі так

звані помилки вибірки, або репрезентативності (відповідності), які

виникають у зв’язку з тим, що відібрана частина сукупності має за

досліджуваною ознакою дещо відмінну структуру порівняно з усією

сукупністю.

Помилки реєстрації, як і при суцільному спостереженні, — це

розходження між записаними даними в процесі спостереження і

дійсними даними. Виникають вони унаслідок недбалого ставлення,

неточності вимірювальних приладів, випадкової описки, різного розу-

міння тих чи інших положень інструкції чи статистичного формуляра.

Помилки репрезентативності — це розходження між середні-

ми величинами або частками ознаки вибіркової і генеральної сукуп-

ностей. Помилки репрезентативності можуть бути систематичними і

випадковими.

Систематичні помилки репрезентативності виникають унаслідок

порушення принципів проведення вибіркового спостереження. Вони

мають тенденційний характер викривлення величини досліджуваної

ознаки у бік її збільшення або зменшення.

Випадкові похибки репрезентативності зумовлені тим, що вибір-

кова сукупність не відтворює точно середні і відносні показники

генеральної сукупності.

При організації вибіркового обстеження важливо уникнути сис-

тематичних помилок. Властиві вибірковому спостереженню випад-

кові похибки усунути неможливо, проте теорія вибіркового методу

дає математичну основу для обчислення розміру і визначення на-

прямів зменшення їх. Завдання полягає в тому, щоб максимально

наблизити показники вибіркової сукупності до показників генераль-

ної сукупності і знайти можливі межі відхилень цих показників,

тобто знайти помилку вибірки. Обумовимо основні позначення ста-

тистичних характеристик, які будуть використовуватись при визна-

ченні помилок вибіркового спостереження (табл. 5.1).

Достовірність вибіркового спостереження забезпечується розра-

хунками його помилок для середньої величини і для частки (питомої

ваги) ознаки, що вивчається:

xXΔ= − — помилка вибірки для середньої величини;

wwWΔ= −

— помилка вибірки для частки.

Ці помилки складаються з помилок репрезентативності і поми-

лок реєстрації. Величини помилок вибірки (репрезентативності) в

основному залежать від:

— обсягу вибірки, бо зі збільшенням числа досліджуваних оди-

ниць результати вибірки дедалі менше відрізнятимуться від резуль-

татів генеральної сукупності;

103

Таблиця 5.1

УМОВНІ ПОЗНАЧЕННЯ СТАТИСТИЧНИХ ХАРАКТЕРИСТИК

ГЕНЕРАЛЬНОЇ І ВИБІРКОВОЇ СУКУПНОСТЕЙ

Сукупність

Характеристика

генеральна вибіркова

Обсяг сукупності N n

Середнє значення ознаки

Загальна дисперсія

Середня з групових дисперсій

Міжгрупова дисперсія

Частка елементів сукупності, які

мають певні значення ознаки

W w

Частка вибіркової сукупності в

генеральній

— D

Кількість серій R r

— варіації досліджуваної ознаки. Чим більше варіює ознака, тим

більше вибіркова середня (частка) відрізняється від генеральної серед-

ньої (частки). Оскільки основним показниками варіації ознаки є диспер-

сія і середнє квадратичне відхилення, то можна стверджувати, що помил-

ка вибірки перебуває у прямій залежності від величин цих показників;

— способу і виду відбору вибіркової сукупності. Для узагальню-

вальної характеристики помилок репрезентативності розраховують

середню помилку вибірки µ, її називають ще стандартом. Для ви-

значення середньої помилки репрезентативності вибірки застосову-

ють формули, наведені у табл. 5.2.

Особливість обчислення помилок репрезентативності для середньої

величини при різних способах відбору полягає в тому, що для її обчис-

лення за основу беруться різні показники дисперсій. При випадковому і

механічному відборі для обчислення помилки вибірки використовуєть-

ся загальна дисперсія

для середньої і w(l – w) — для частки.

Коли відбір одиниць здійснюється з окремих типово однорідних

груп, виділених за відповідною ознакою, варіації групових середніх

немає, і похибка типової вибірки залежить від середньої величини з

групових

для середньої і w(l – w) — для частки.

У разі серійної вибірки, яка передбачає суцільне спостереження

одиниць у відібраних серіях, похибка вибірки залежить не від числа

обстежених одиниць сукупності, а від кількості відібраних серій.

Похибка вибірки залежатиме не від варіації ознаки в усій сукупності, а

від варіації серійних середніх, яка вимірюється міжгруповою диспер-

сією середньої

. При обчисленні середньої помилки вибірки для

частки ознаки в основі розрахунку є міжгрупова (міжсерійна) дисперсія

вибіркової частки

104

()

−

∑

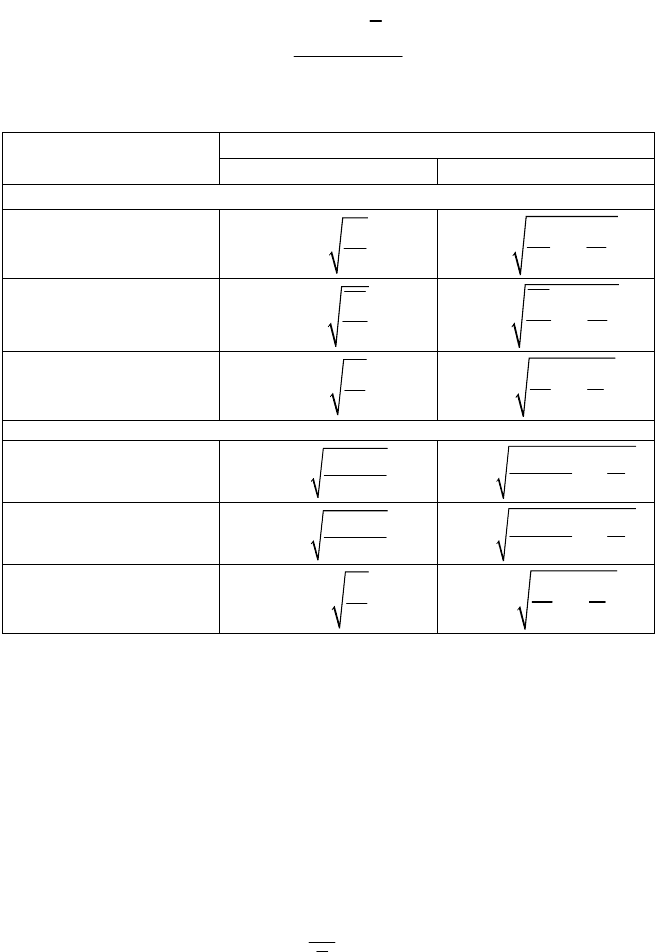
Таблиця 5.2

СЕРЕДНЯ ПОМИЛКА ВИБІРКИ

Метод вибору

Спосіб вибору

повторний безповторний

Помилка вибірки для середньої величини

Випадковий і

механічний

Δ=

Δ= −

⎛⎞

⎜⎟

⎝⎠

Типовий

(районований)

Δ=

Δ= −

⎛⎞

⎜⎟

⎝⎠

Серійний

Δ=

Δ= −

⎛⎞

⎜⎟

⎝⎠

Помилка вибірки для частки

Випадковий і

механічний

(1 )ww

−

Δ=

(1 )

ww n

−

Δ= −

⎛⎞

⎜⎟

⎝⎠

Типовий

(районований)

(1 )ww

−

Δ=

(1 )

ww n

−

Δ= −

⎛⎞

⎜⎟

⎝⎠

Серійний

Δ=

Δ= −

⎛⎞

⎜⎟

⎝⎠

Похибка вибірки для частки ознаки при серійному відборі залежить

від числа серій у генеральній сукупності R і числа відібраних серій r.

Безповторний відбір гарантує точніші результати, оскільки він

виключає можливість обстеження одних і тих самих одиниць при

відборі з генеральної сукупності.

У статистичному аналізі часто постає потреба порівняння похиб-

ки вибірки різних ознак або однієї і тієї самої ознаки в різних сукуп-

ностях. Такі порівняння виконують за допомогою розрахунку віднос-

ної похибки, яка показує, на скільки відсотків вибіркова оцінка може

відхилятися від параметра генеральної сукупності. Відносна стандартна

похибка середньої — це коефіцієнт варіації вибіркових середніх:

100

=⋅

105

Для узагальнювальної характеристики помилки вибірки поряд із

середньою розраховують і граничну похибку вибірки. Стверджува-

ти, що дана генеральна середня не вийде за межі середньої помилки

вибірки можна лише з певним ступенем імовірності.

У випадку вибіркового спостереження гранична похибка репре-

зентативності ∆ може бути більшою чи дорівнювати або меншою

від середньої помилки репрезентативності. Тому граничну похибку

репрезентативності обчислюють з певною ймовірністю Р, якій від-

повідає t-разове значення середньої помилки репрезентативності.

Відповідно до показника кратності помилки t формула граничної

похибки репрезентативності має такий вигляд:

tΔ=

де ∆ — гранична похибка вибірки; µ — середня похибка вибірки;

t — коефіцієнт довіри, який залежить від імовірності, з якою гаран-

тується значення граничної похибки вибірки.

Формула граничної похибки вибірки випливає з основних поло-

жень теорії вибіркового методу, сформульованих у теоремах імовір-

ностей, що відображують закон великих чисел.

Однією із головних теорем, яку покладено в основу теорії вибір-

кового методу, є теорема П. Л. Чебишева, на основі якої було дове-

дено, що з імовірністю, як завгодно близькою до одиниці, можна

стверджувати, що при достатньо великому числі незалежних спо-

стережень вибіркова середня буде мало відрізнятися від генеральної

середньої при проведенні повторної вибірки.

Академік А.А. Марков довів теореми про збереження цієї умови для

залежних спостережень (без повторної вибірки). Академік A. M. Ля-

пунов обґрунтував положення про те, що ймовірність відхилень ви-

біркової середньої від генеральної середньої при достатньо велико-

му обсязі вибірки та обмеженій дисперсії генеральної сукупності

підпорядковується закону нормального розподілу. Ймовірність цих

відхилень при різних значеннях t визначається за формулою:

()

2π

xed

−

=τ

∫

Значення цього інтеграла при різних значеннях t табульовані і

наводяться в спеціальних таблицях, наприклад:

t = 1 Р (∆ ≤ µ ) = 0,683

t = 2 Р (∆ ≤ µ ) = 0,954

t = 3 P (∆ ≤ µ ) = 0,997

t = 4

(∆ ≤ µ )

= 0,999

Ці показники означають, що з імовірністю 0,683 можна стверд-

жувати, що гранична похибка вибірки не перевищує µ, тобто у

68,3 % випадків помилка репрезентативності не виходить за межі

106

± µ. Інакше, в 683 випадках із 1000 помилка репрезентативності не

перевищує одного значення середньої помилки. З імовірністю 0,954

можна стверджувати, що помилка репрезентативності не перевищує

± 2 µ, з ймовірністю 0,997 — не перевищить ± 3 µ. З імовірністю

0,999, тобто дуже близькою до одиниці, можна очікувати, що різни-

ця між вибірковою і генеральною середніми не перевищить чотири-

разової помилки вибірки.

Гранична похибка вибірки розраховується за вибірковим спосте-

реженням залежно від видів і способів відбору. Вона дає можливість

встановити, в яких межах лежать значення генеральної середньої

або частки. У табл. 5.3 наведено формули для обчислення граничної

похибки вибірки залежно від виду та способу її відбору.

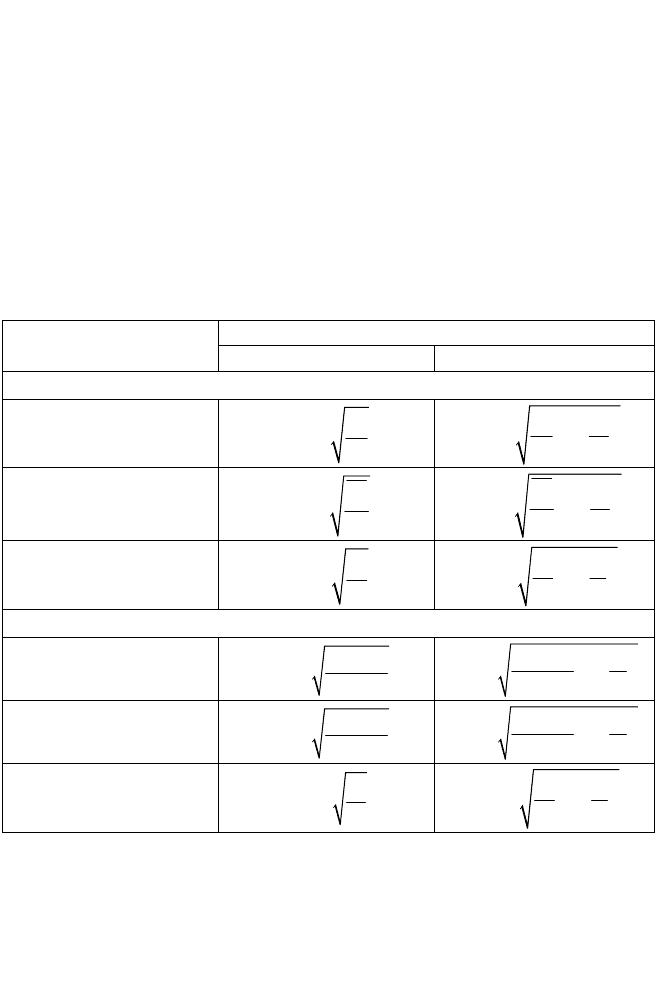
Таблиця 5.3

ГРАНИЧНІ ПОМИЛКИ ВИБІРКИ

Метод вибору

Спосіб вибору

повторний безповторний

Похибка вибірки для середньої величини

Випадковий

і механічний

Δ=

Δ= −

⎛⎞

⎜⎟

⎝⎠

Типовий

(районований)

Δ=

Δ= −

⎛⎞

⎜⎟

⎝⎠

Серійний

Δ=

Δ= −

⎛⎞

⎜⎟

⎝⎠

Похибка вибірки для частки

Випадковий і

механічний

(1 )ww

−

Δ=

(1 )

ww n

−

Δ= −

⎛⎞

⎜⎟

⎝⎠

Типовий

(районований)

(1 )ww

−

Δ=

(1 )

ww n

−

Δ= −

⎛⎞

⎜⎟

⎝⎠

Серійний

Δ=

Δ= −

⎛⎞

⎜⎟

⎝⎠

За допомогою формул граничної похибки вибірки визначають:

— довірчі межі генеральної середньої і частки з певною ймовірністю;

— ймовірність того, що відхилення між вибірковими і генераль-

ними характеристиками не перевищує визначену величину;

— необхідну чисельність вибірки, яка із заданою ймовірністю

забезпечує очікувану точність вибіркових показників.

107

КОНТРОЛЬНІ ПИТАННЯ

1. Чому при вибірковому спостереженні виникають помилки? Як їх кла-

сифікують?

2. Чи можна уникнути систематичної помилки?

3. Як визначають помилки вибірки для середньої і частки?

5.4. Визначення обсягу вибірки

Під час вибіркового спостереження важливо правильно визначи-

ти необхідну чисельність обсягу вибірки, яка з відповідною ймовір-

ністю забезпечує встановлену точність результатів спостереження.

Звичайно, чим більша вибірка, тим точніші оцінки характеристик

сукупності. Але треба мати на увазі, що надмірний обсяг вибірки

призводить до зволікання зі строками дослідження, зайвих затрат

часу і коштів, а недостатній обсяг дає результати з великою похиб-

кою репрезентативності.

Визначення необхідного обсягу вибірки залежить від алгебрич-

ного перетворення формул граничної похибки вибірки при різних

способах відбору. Формули необхідного обсягу вибірки при повтор-

ному і безповторному відборах наведено у табл. 5.4.

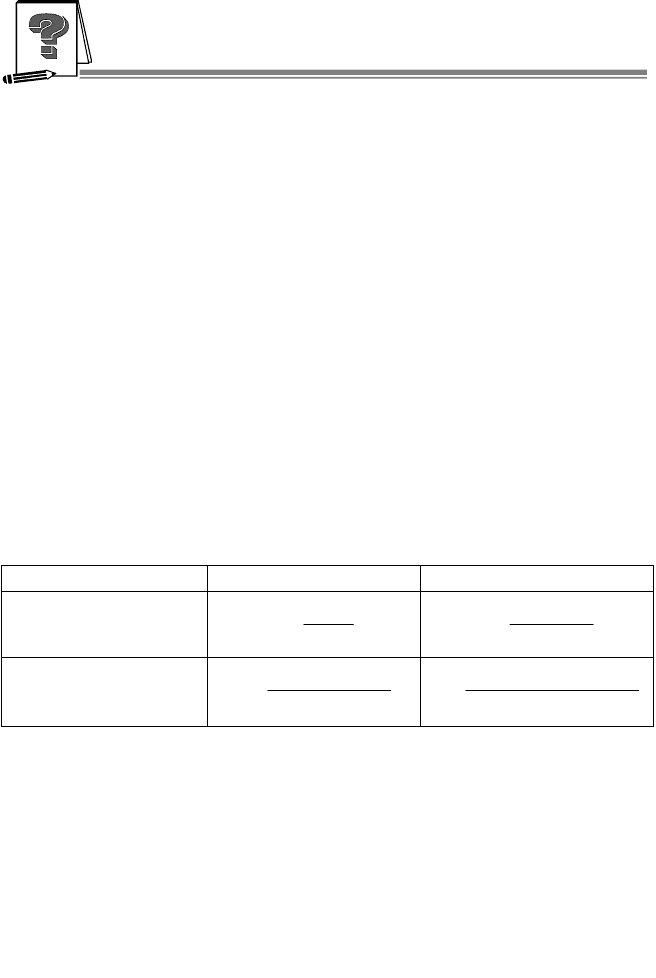
Таблиця 5.4

НЕОБХІДНИЙ ОБСЯГ ВИБІРКИ

Спосіб відбору Визначення середньої

Визначення частки

Повторний

()

σt

()

(1 )tw w

−

Безповторний

()

σtN

xNt

Δ+σ

()

(1 )

tw wN

wNtw w

−

Δ+−

Аналіз наведених у табл. 5.4 формул дає підстави стверджувати,

що обсяг вибірки залежить від:

— розміру граничної похибки (чим точніші результати треба

отримати, тобто з меншою похибкою вибірки, тим більшою має бу-

ти чисельність вибірки);

— показників варіації ознаки та частки (чим більші варіації, тим

більше треба взяти одиниць для вибіркового спостереження);

— імовірності, з якою вимагається гарантувати результати вибір-

ки (чим більша ймовірність, тим більший коефіцієнт кратності, тим

більшою має бути чисельність вибірки).

108

У практичних розрахунках обсягу вибірки стикаються з тими ж

труднощами, що і при розрахунку середньої помилки, а саме — від-

сутні показники мінливості одиниць сукупності σ та w(l – w).

Проблему вирішують таким чином: замість фактичних значень σ

та

w підставляють їх наближені значення, встановлені або на підставі попе-

реднього обстеження, або на підставі пробних вибіркових обстежень.

Для частки ознаки в сукупності питання про дисперсію вирішу-

ється простіше. Справа в тому, що дисперсія альтернативної ознаки

змінюється так: при w(l – w) будемо мати:

w = 0,2 0,2 (1– 0,2) = 0,16

w = 0,3 0,3 (1– 0,3) = 0,21

w = 0,4 0,4 (1– 0,4) = 0,24

w = 0,5 0,5 (1– 0,5) = 0,25

w = 0,6 0,6 (1– 0,6) = 0,24

w = 0,7 0,7 (1– 0,7) = 0,21

w = 0,8 0,8 (1– 0,8) = 0,16

Це означає, що максимальне значення дисперсії альтернативної

ознаки може бути 0,25. Для визначення необхідного обсягу вибірки

у процесі дослідження частки в розрахунках набувають максималь-

ного значення дисперсії альтернативної ознаки 0,25.

Необхідний обсяг вибірки в разі серійного відбору визначають як

відбір певної кількості серій, які забезпечують з відповідною ймовір-

ністю потрібну точність результатів дослідження. Для повторного

відбору необхідний обсяг вибірки

δt

r =

а для безповторного:

222

Δ+δ

У статистичній практиці вибіркове спостереження з великих ма-

сивів генеральної сукупності часто здійснюють у вигляді комбінова-

ної, ступінчастої або кількафазної вибірки. Вибіркова сукупність у разі

комбінованої вибірки формується внаслідок ступінчастого відбору.

Загальна помилка для комбінованої вибірки складається з поми-

лок, які можливі на кожному ступені, і визначається як корінь квад-

ратний з квадратів помилок відповідних вибірок. Наприклад, якщо

серійну вибірку скомбінувати з випадковою або механічною, то гра-

нична похибка вибірки буде визначатись так:

rRnN

⎛⎞⎛ ⎞

Δ= − + −

⎜⎟⎜ ⎟

⎝⎠⎝ ⎠

109

У разі моментного методу спостереження гранична похибка частки

визначається як для звичайної повторної простої випадкової вибірки.

Відбір моментів здійснюють за схемою механічної вибірки або за

схемою випадкової вибірки за таблицею випадкових чисел. Другий

спосіб доцільно застосовувати в тих випадках, коли спостереження

має бути для об’єкта несподіваним, аби не порушувати його звичай-

ний життєвий ритм.

Визначають обсяг моментних спостережень за формулою гранич-

ної похибка випадкової повторної вибірки. Відбір у моментних спо-

стереженнях завжди безповторний, однак формулу безповторного

відбору застосовувати не можна, оскільки обсяг генеральної сукуп-

ності моментів життєдіяльності визначити неможливо, він нескін-

ченний, якщо момент спостереження досить короткий. А тому необ-

хідна кількість моментів спостереження дорівнює

0, 25t

n =

або якщо прийняти довірчу ймовірність Р = 0,954, тобто коефіцієнт

довіри t = 2, тоді

0, 25 2 1

⋅

ΔΔ

Кінцевою метою будь-якого вибіркового спостереження є поши-

рення його характеристик на генеральну сукупність. На практиці

застосовують різні способи поширення вибіркових даних.

Спосіб прямого переліку використовують у тому випадку, коли

метою вибіркового обстеження є визначення обсягу ознаки в гене-

ральній сукупності.

Якщо вибіркове спостереження проводять задля уточнення ре-

зультатів суцільного спостереження, застосовують спосіб поправко-

вих коефіцієнтів.

КОНТРОЛЬНІ ПИТАННЯ

1. Чи впливає обсяг вибірки на її точність і якою мірою?

2. Від чого залежить обсяг вибірки?

3. Як визначають необхідну чисельність вибірки в разі повторного і

безповторного відбору?

110

6.1. Суть рядів динаміки

У природі всі явища і процеси перебувають у неперервному зв’яз-

ку і зміні. Процес розвитку явища у часі називається динамікою.

Для глибокого і ґрунтовного вивчення зміни в часі природних явищ

під упливом різних факторів використовують спеціальну систему ста-

тистичних методів під загальною назвою «статистична динаміка».

Статистична динаміка займається вивченням об’єктивних за-

кономірностей поступального неперервного розвитку соціально-

економічних і природних явищ у часі на основі спостереження задля

оптимального господарського управління й охорони навколишнього

середовища. Первинні, відібрані на основі науково обґрунтованої

методики, спостережувані дані використовуються для побудови ди-

намічних рядів.

Динамічний ряд — це статистичні показники, розташовані в

хронологічній послідовності, які характеризують розвиток того чи

іншого явища у часі.

Для будь-якого динамічного ряду характерні перелік хронологіч-

них дат (моментів) або інтервалів часу і конкретні значення відповід-

них статистичних показників. Окремі числові значення розмірів

явищ називають рівнями ряду. Рівень ряду відображає стан явища,

досягнутий за будь-який період або на певний момент часу. Перший

показник ряду називають початковим, а останній — кінцевим.

При вивченні динаміки важливі не лише числові значення рівнів,

а й послідовність їх. Як правило, часові інтервали між рівнями одна-

кові — доба, декада, місяць, рік тощо.

За ознакою часу динамічні ряди поділяють на інтервальні (періо-

дичні) і моментні. Динамічний ряд, в якому хронологічний перелік

ведеться у вигляді проміжків часу (років, місяців, діб), називається

інтервальним динамічним рядом.

В інтервальному ряді значення рівня визначається залежно від

тривалості часового інтервалу і він є агрегованою величиною. Харак-

терна особливість інтервального динамічного ряду полягає у залеж-

ності величини рівня від проміжку часу. Показники ряду, як прави-

ло, можна додавати і ці показники мають конкретний зміст. Наприк-

РЯДИ ДИНАМІКИ

РОЗ

ІЛ