Михайлов В.С, Кудрявцев В.Г, Давыдов В.С. Навигация и лоция
Подождите немного. Документ загружается.

18.4. Средняя квадратическая погрешность линии положения
Для большинства навигационных параметров навигационные изолинии являются кривыми
линиями, построение которых на карте вызывает определенную трудность.
В этих случаях навигационная изолиния может быть заменена небольшим по длине отрезком
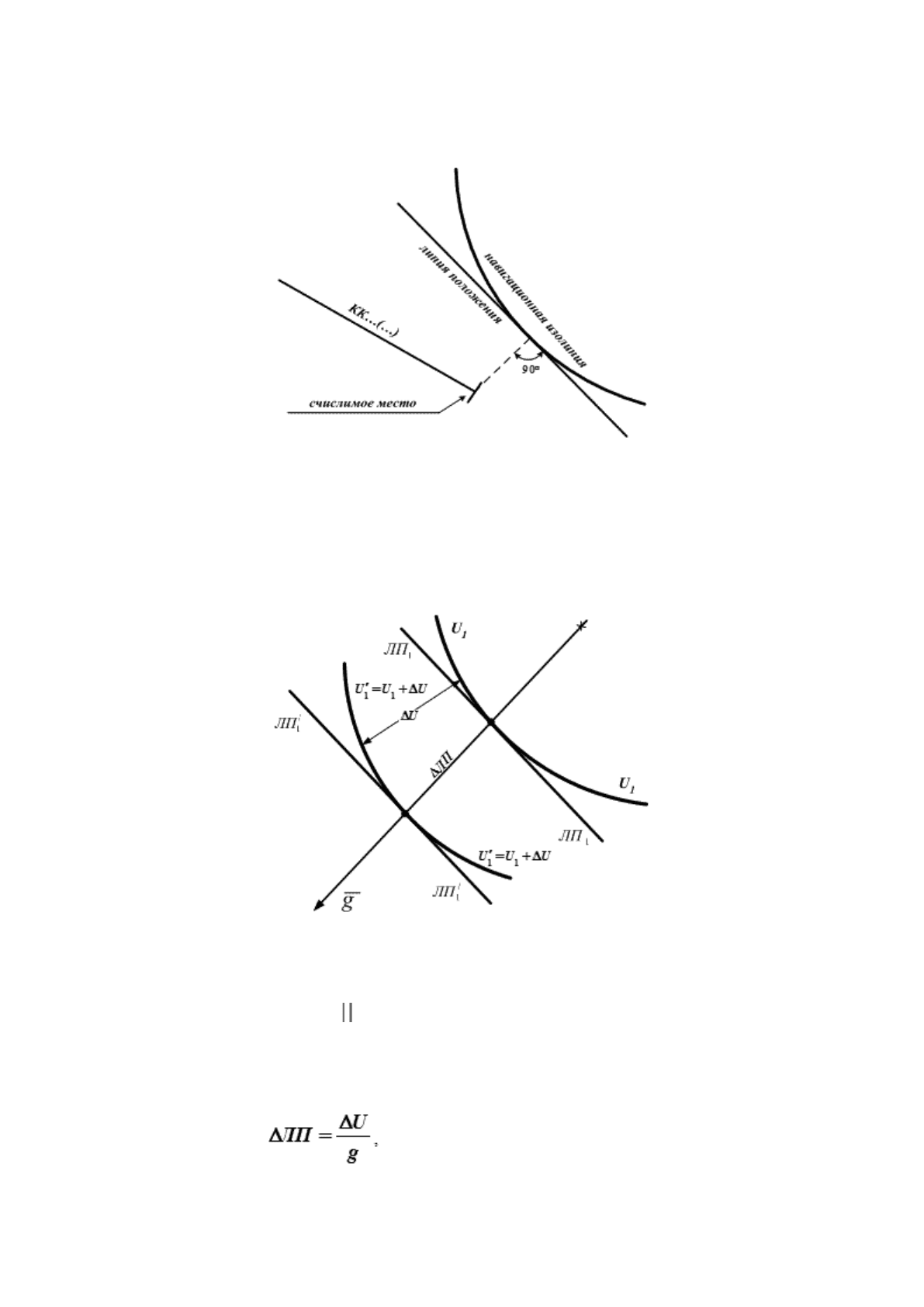
прямой линии, касательным к изолинии вблизи счислимого места судна (рис. 18.6).
Рис. 18.6. Навигационная изолиния и линия положения
Эти прямые линии, которые заменяют навигационные изолинии, называются линиями положения
→ отрезки прямых линий, касательные к навигационным изолиниям вблизи счислимого места судна.
Замена навигационных изолиний линиями положения позволяет простыми приемами находить
обсервованное место судна на карте и производить оценку его точности.
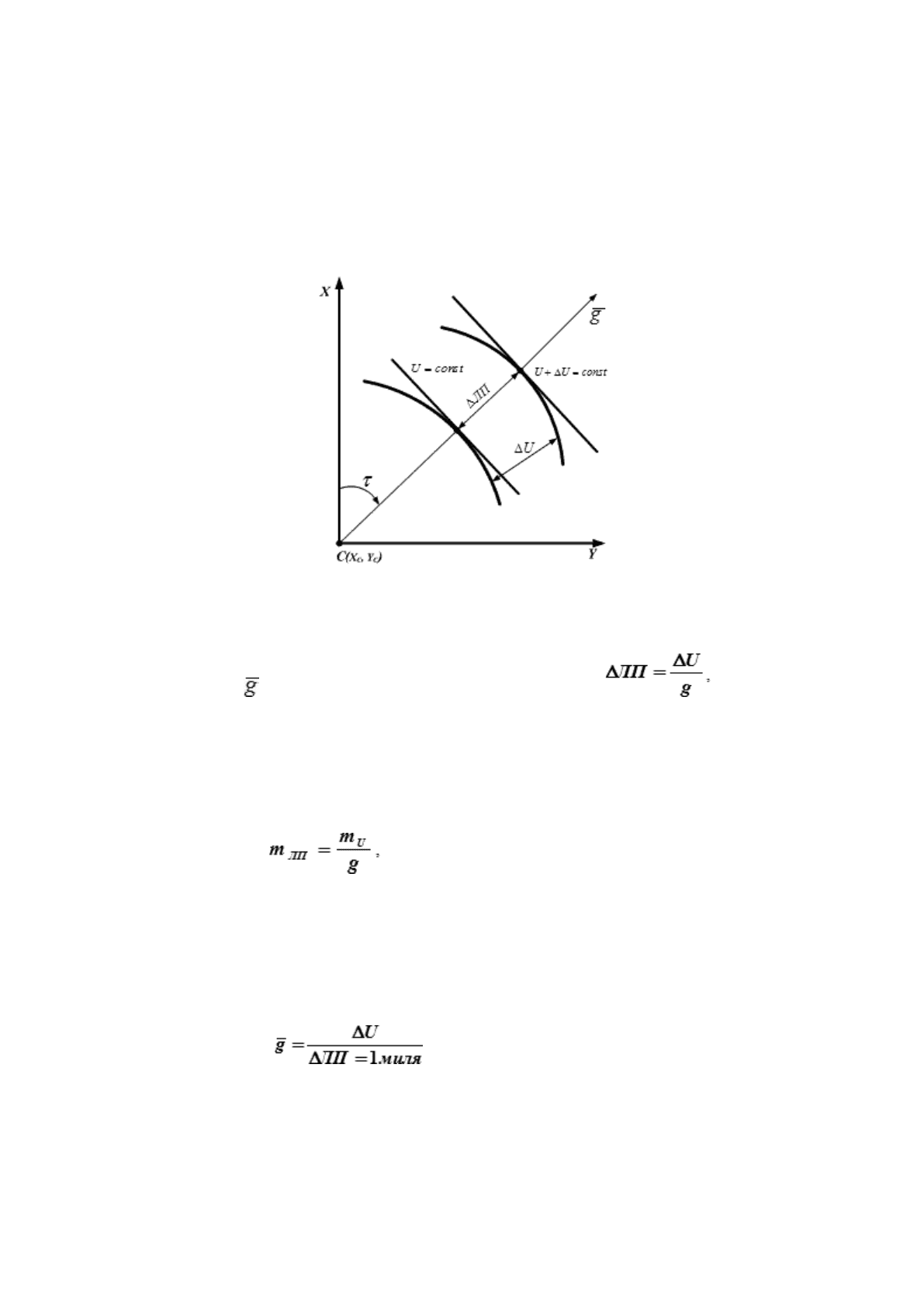
Линия положения (ЛП) характеризуется следующими свойствами (рис. 18.7):
Рис. 18.7. Свойства навигационной линии положения
1. При малом изменении величины навигационного параметра (Δ U) линии положения смещаются
параллельно друг другу (ЛП′
1
ЛП
1
).
2. Величина параллельного смещения линии положения (Δ ЛП) находится в пропорциональной
зависимости от величины изменения навигационного параметра (ΔU).
Математически это свойство выражается формулой
(18.12)
где
ΔЛП – линейное смещение линии положения в единицах длины (мили);
ΔU – изменение навигационного параметра в его единицах;
g – градиент навигационного параметра (его численное значение).
Неизбежные случайные погрешности, допускаемые при измерениях навигационных параметров
(пеленгов, расстояний и пр.) вызывают погрешность и линии положения.
Рассмотрим, каковы будут эти погрешности в зависимости от значений градиентов (g) и
погрешностей измерения навигационного параметра (m
U
).
Допустим, что в результате измерения какого-то навигационного параметра была получена
навигационная изолиния, которая в общем случае выражается как:
U = f (x, y)
(18.13)
Заменим вблизи счислимого места навигационную изолинию отрезком прямой ей касательным –
линией положения (рис. 18.8).
Пусть при измерении навигационного параметра была допущена случайная погрешность ΔU. В
результате этой погрешности линия положения сместится по нормали на некоторое расстояние ΔЛП.
Рис. 18.8. Свойства навигационной линии положения
Величина смещения линии положения в зависимости от погрешности навигационного параметра
(ΔU) и его градиента ( ) найдется по формуле (18.12), то есть (2-е свойство линии
положения).
Градиент навигационного параметра (g) для данной точки – величина постоянная.
Учитывая то, что «…квадрат средней квадратической погрешности функции равен сумме квадратов
произведений частных производных функций по каждому аргументу на среднюю квадратическую
погрешность соответствующего аргумента…» формула СКП линии положения (m
ЛП
) применительно к
изолинии, выражаемой линейным уравнением U = f (x, y), будет иметь вид
(18.14)
где
m
ЛП
– СКП линии положения (мили);
m
U
– СКП измерения навигационного параметра;
g – градиент навигационного параметра.
Значение градиента навигационного параметра означает: на какую величину нужно ошибиться в
получении (измерений) навигационного параметра, чтобы линия положения сместилась точно на одну
милю.
(18.15)
Если с РЛС мы сняли расстояние до ориентира с ошибкой в 1 милю, значит, и линия положения
сместится тоже на 1 милю. Из этого следует, что градиент расстояния равен единице, то есть:
g
D
= 1
(18.16)
Если до берегового ориентира расстояние D = 1 миля, то для смещения линии положения тоже на 1
милю мы должны снять пеленг на этот ориентир с ошибкой в 1 радиан = 57,3° (если до маяка D = 57,3
мили → ошибка в пеленге = 1°).
Значит, для пеленга:
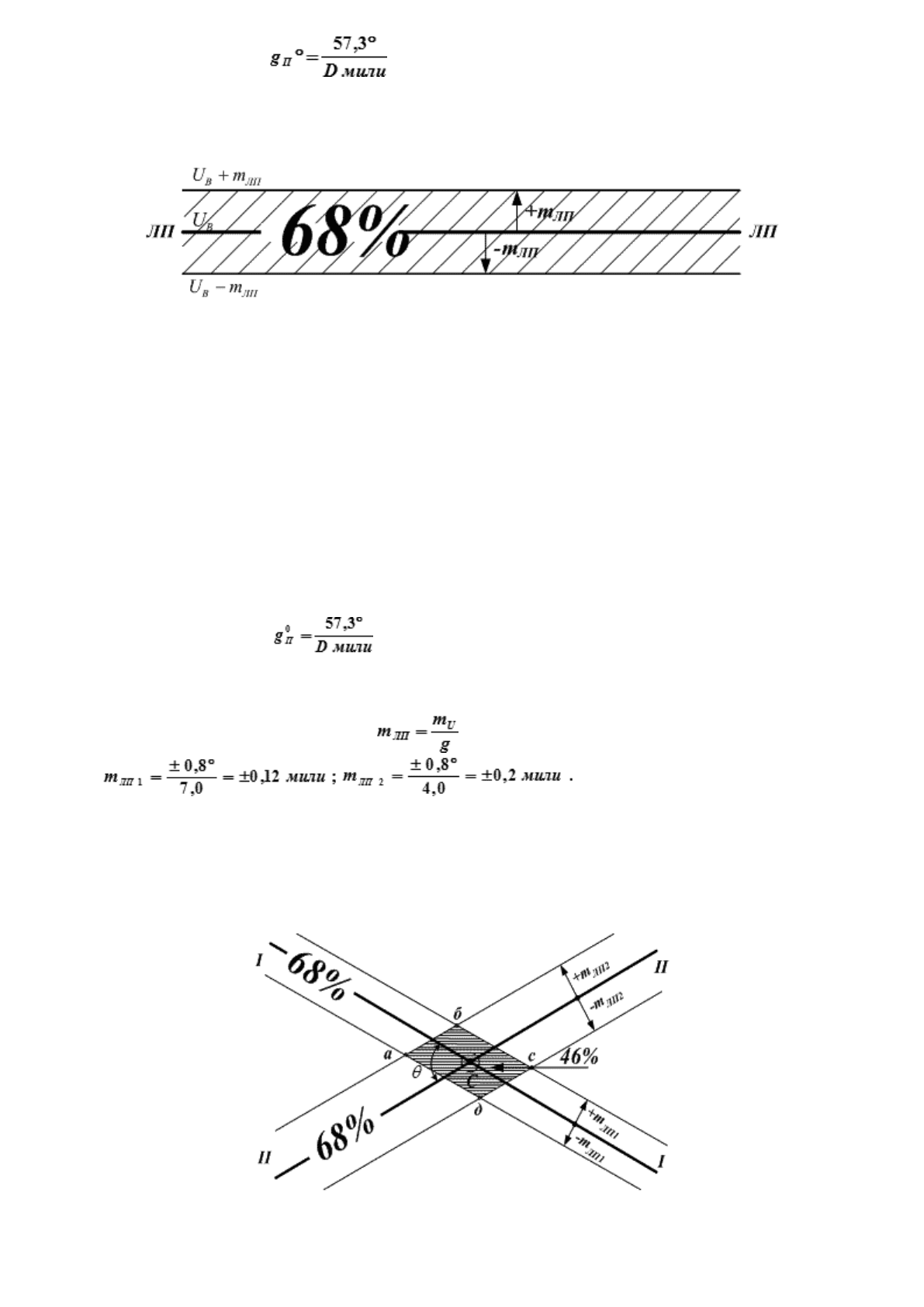
(18.17)
Значения градиентов навигационных параметров используемых в судовождении известны и
приведены в табл. 5.47 «МТ-2000» (с. 470÷482).
Графически СКП линии положения можно пояснить следующим образом (рис. 18.9).
Рис. 18.9. Среднеквадратическая погрешность линии положения
Если проложить на карте навигационную изолинию или линию положения, то при анализе
погрешности определения места следует считать, что судно находится в полосе шириной ±m
ЛП
, а не
точно на проведенной линии (ЛП).
Так как m
ЛП
является СКП, то вероятность нахождения судна в полосе ±m
ЛП
равна ≈ 68%.
Можно сказать и так, что «… вероятнейшее значение навигационного параметра (U
В
),
соответствующее данной линии положения (навигационной изолинии), находится в полосе ±m
ЛП
с
вероятностью Р = 0,68».
Пример расчета СКП линии положения (m
ЛП
).
На 2 ориентира измерены визуальные пеленги с СКП – m°
П
= ±0,8°. Расстояния от обсервованного
места судна до ориентиров соответственно равны: D
1
= 8,2 мили и D
2
= 14,2 мили.
Рассчитать: СКП линий положения (m
ЛП1
и m
ЛП2
).
Решение.
1. По формуле (18.17) рассчитываем значения градиента навигационного параметра
(пеленга) для обсервованной точки:
g°
П1
= 57,3° / 8,2 мили = 7,0; g°
П2
= 57,3° / 14,2 мили = 4,0.
2. По формуле (18.14) рассчитываем СКП линий положения:
Таким образом, получили значения полуширины полос в пределах которых обсервованное место
судна находится с вероятностью ≈ 68% (Р = 0,68).
18.5. Радиальная (круговая) СКП обсервованного места судна
Рис. 18.10. Погрешность обсервованного места судна
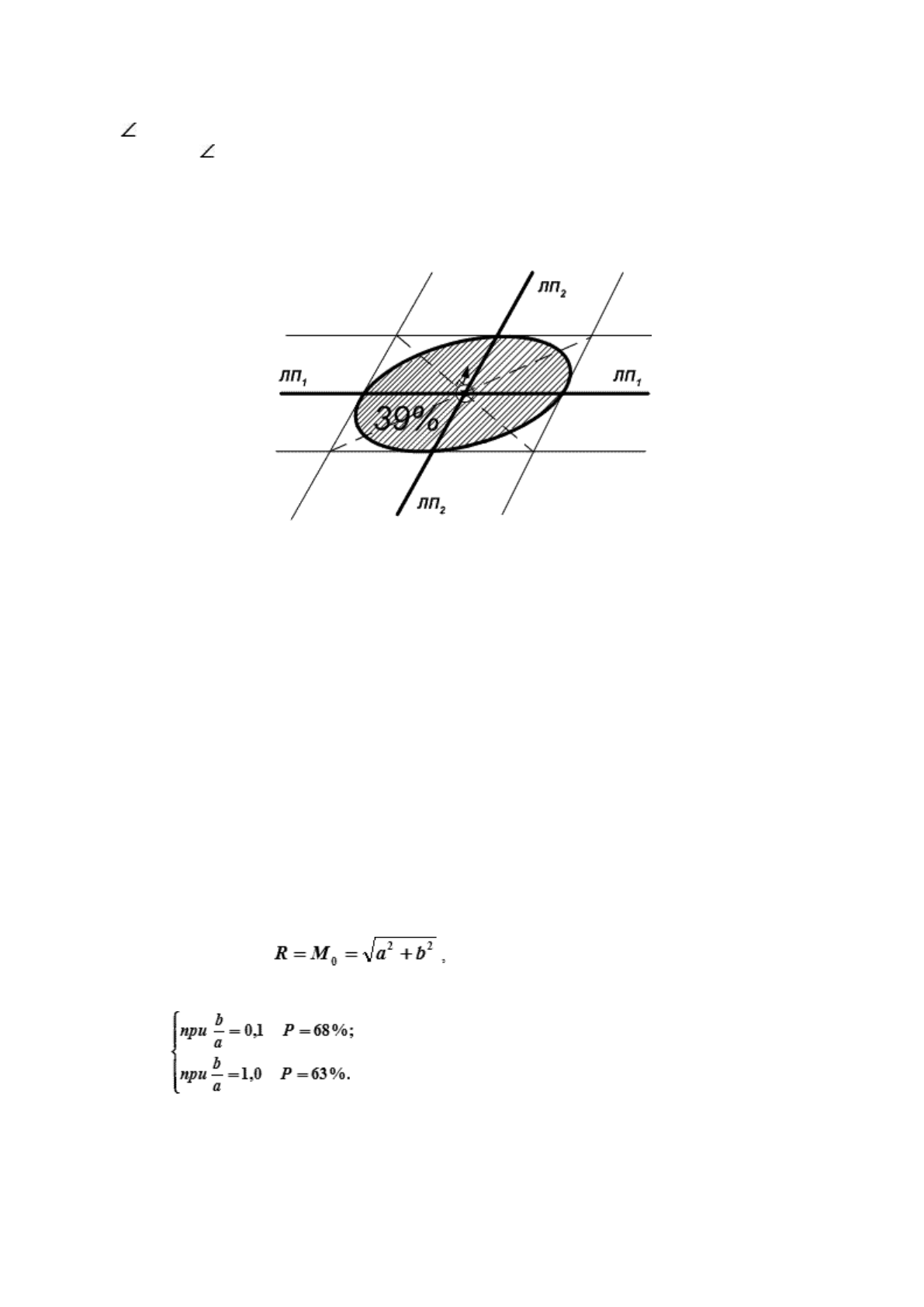
Поскольку обсервованное место судна образуется пересечением минимум двух линий положения,
а, значит, и двух полос, то на путевой карте мы получим не точку С (рис. 18.10), а так называемую
фигуру погрешностей «абсд». Размеры этой фигуры при неизменных m
ЛП
будут зависеть, прежде
всего, от угла пересечения линий положения – угла θ.
При θ = 90° площадь фигуры погрешностей наименьшая, а при m
ЛП1
= m
ЛП2
– квадрат. Но, чем
меньше будет этот θ, тем больше будет площадь фигуры погрешностей «абсд».
Вероятность нахождения обсервованного места судна в этой фигуре погрешностей равна
произведению вероятностей нахождения места судна в каждой из полос, то есть: Р = 0,68 · 0,68 ≈ 0,46
(46%).
Однако, точность места судна принято оценивать не параллелограммом «абсд» (ромбом,
квадратом) погрешностей, а эллипсом, вписанным в этот параллелограмм (рис. 18.11).
Рис. 18.11. Эллиптическая погрешность обсервованного места судна
Эллипс погрешностей обладает следующими свойствами:
1. Размеры и ориентировка эллипса погрешностей дают наглядное представление о точности
определения места по различным направлениям.
2. Вероятность того, что случайная погрешность не выйдет за пределы эллипса погрешностей
больше, чем для любой другой фигуры погрешности, имеющей такую же площадь.
3. Среди всех фигур, в пределах которых, вероятность нахождения судна одинакова, эллипс
погрешностей имеет наименьшую площадь.
Вероятность нахождения места судна в эллипсе погрешностей равна Р = 0,39(39%).
Но эллипс погрешностей, из-за сложности его построения, применяют только при решении
специальных задач судовождения.
В повседневной практике используют более грубую, но более простую оценку точности места
судна – через радиальную (круговую) СКП – М
0
.
Радиальная (круговая) СКП обсервованного места (М
0
) построена на полуосях эллипса
погрешностей (рис. 18.12).
(18.18)
Вероятность нахождения обсервованного места судна в круге радиусом R = M
0
зависит от
соотношения полуосей эллипса погрешностей.
Например:
В общем случае, вероятность нахождения места судна в круге радиусом R = M
0
принимается
равной 63% (0,63), так как в большинстве случаев соотношение полуосей эллипса b/a близко к 1.
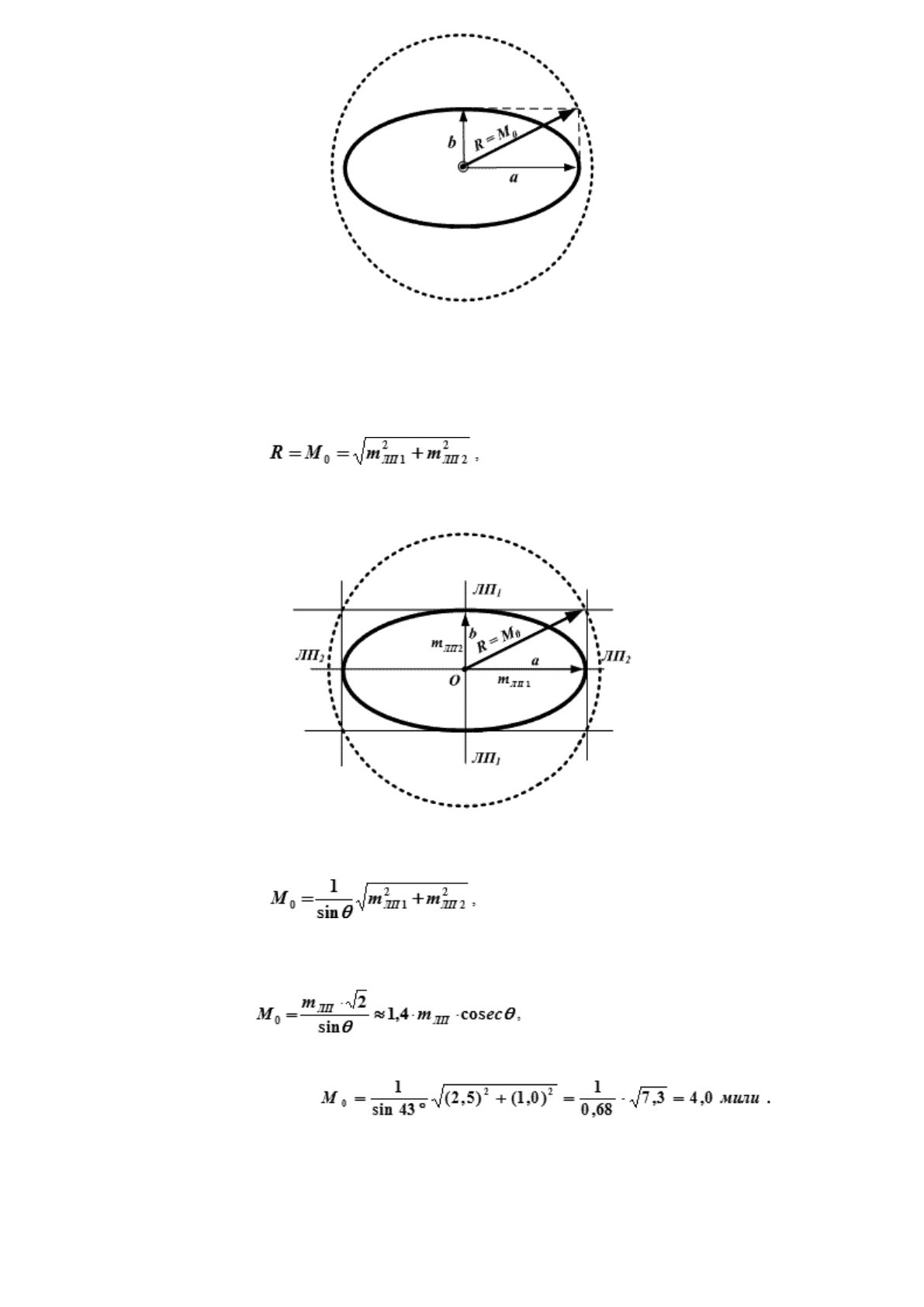
Рис. 18.12. Радиальная (круговая) СКП места судна
Как видно из рис. 18.13 при θ = 90° (sin θ = 1) полуоси эллипса погрешностей численно равны по
своей величине СКП линий положения (а = m
ЛП1
, b = m
ЛП2
) и формулу (18.18) для этого случая можно
записать как:
(18.19)
Для общего же случая (когда θ ≠ 90° и sin θ < 1) радиальная (круговая) СКП обсервованного места
судна M
0
в зависимости от СКП линий положения (m
ЛП1
и m
ЛП2
) и угла их пересечения θ определяется по
общей формуле (18.20):
Рис. 18.13. Радиальная (круговая) СКП обсервованного места судна
(18.20)
Эта формула является основной для расчета величины радиальной (круговой) СКП места судна,
определенного по двум любым линиям положения.
При равноточных наблюдениях, то есть когда m
ЛП1
= m
ЛП2
формула (18.20) примет вид:
(18.21)
Решим задачу расчета M
0
на примере:
Дано: m
ЛП1
= ±2,5 мили; m
ЛП2
= ±1,0 мили; θ = 43°; M
0
– ?
Решение: по формуле (18.20)
Если теперь из обсервованного места судна на путевой карте провести окружность радиусом R =
M
0
= 4,0 мили, то можно сказать, что фактическое место судна находится в пределах площади этой
окружности с вероятностью Р = 63% (0,63).
18.6. Оценка и анализ точности счислимого места судна
18.6.1. Средняя квадратическая и предельная погрешности счислимого места судна
Радиальная (круговая) СКП счисления (М
Сt
) характеризует счислимое место судна на какой-то
момент времени только для случая, когда исходное (начальное) место судна имело погрешность,
равную нулю.
В практике такого не бывает. Ведь даже место причала или швартовной бочки нанесено на карте с
какой-то погрешностью.
А как же определяется СКП счислимого места на любой момент времени (М
СЧ
), если исходной
точкой было место с начальной погрешностью М
0
?
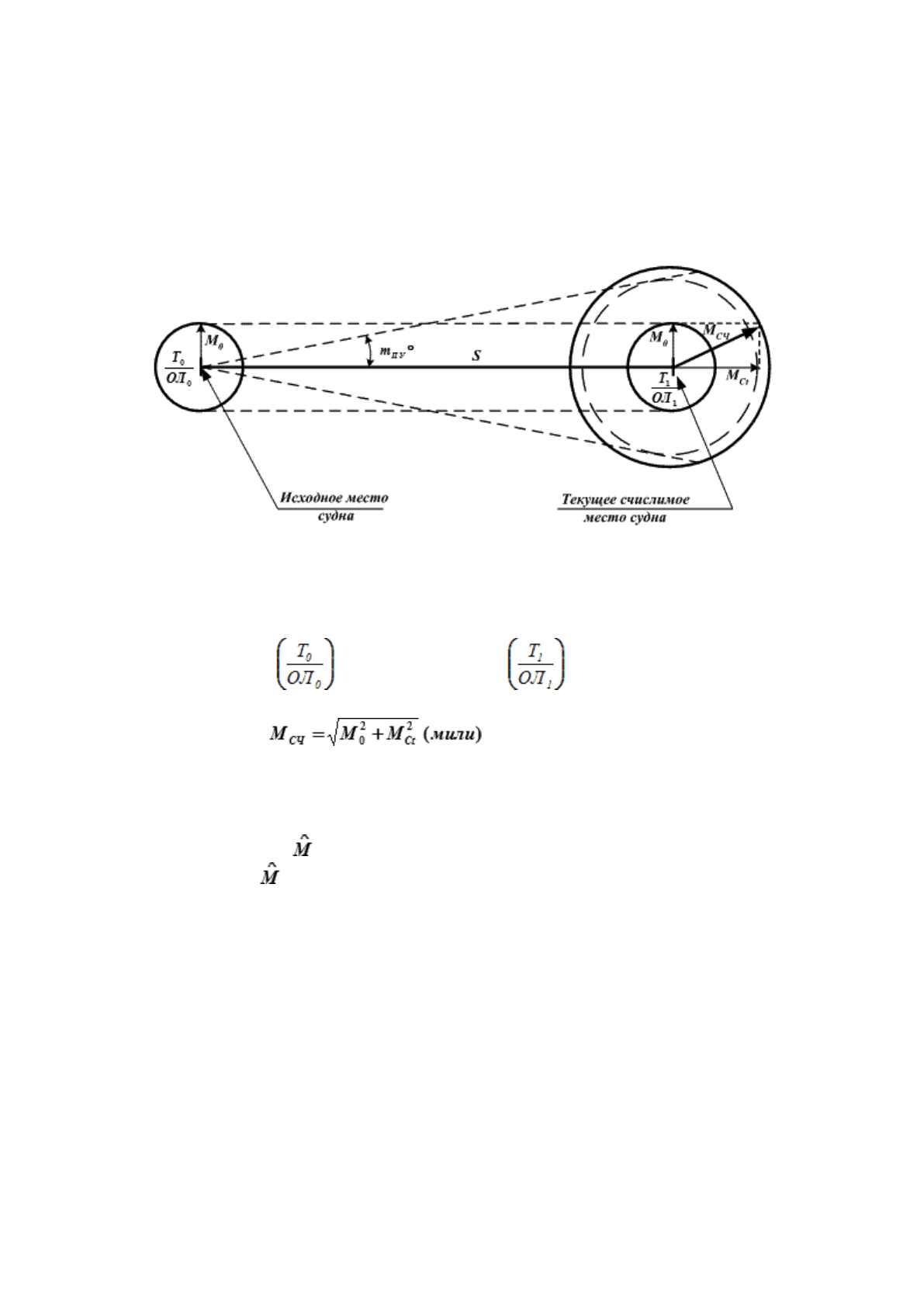
Рис. 18.14. Радиальная (круговая) СКП счислимого места судна
Погрешность счислимого (текущего) места судна складывается квадратически (рис. 18.14) из
погрешности исходной обсервации (М
0
) или исходной точки и погрешности счисления (М
Сt
) за время
плавания от исходной точки до счислимого места – t = T
1
– T
0
.
Математически радиальная (круговая) СКП счислимого места (М
СЧ
) выражается формулой:
(18.22)
Рассчитанная по формуле (18.22) СКП счислимого места (М
СЧ
) имеет вероятность Р ≈ 63% (0,63). В
некоторых же случаях необходимо иметь более высокую вероятность счислимого места, то есть знать
радиус круга, внутри которого фактическое место судна находится с Р > 63% (0,63).
Требуется знать предельную погрешность счислимого места с заданной вероятностью (Р).
Предельная погрешность ( ) математически выражается общей формулой:
= M · K
P2
(18.23)
где
М – радиальная (круговая) СКП места судна;
K
P
− коэффициент по заданной вероятности (P = 90% − K
P
= 1,5; P = 95% − К
P
= 1,73; Р = 98% − К
P
= 2,0; Р = 99% − К
P
= 2,15; Р = 99,9% − К
P
= 2,7).
См. табл. 1в «МТ-75» (с. 61) или табл. 4.13 «МТ-2000» (с. 406) «Вероятность радиальной
погрешности» для соотношения полуосей эллипса погрешностей e = b / a = 1,0. или табл. 4.15 «МТ-
2000» (с. 407) «Вероятность радиальной погрешности при круговом распределении мест» → см. табл.
18.2 и 18.3.
Точность счислимого места судна обязательно рассчитывается:
1. → в часы, кратные 4-м, при плавании по счислению;
2. → при передаче штурманской вахты;
3. → с прибытием по счислению в назначенную точку встречи (район);
4. → при подходе к побережью или к навигационной опасности и других случаях, по указанию
капитана.
Для определения возможности входа по счислению в узкость, на фарватер, в назначенную полосу
движения и др. точность текущего места следует оценивать предельной погрешностью (
СЧ
) с
вероятностью Р = 0,99 (99%).
18.6.2. Выбор безопасного пути судна с учетом точности его плавания
При плавании судна в море возникает необходимость рассчитать – на каком расстоянии следует
пройти (обойти) навигационную опасность, чтобы безопасно «разойтись» с ней с заданной
вероятностью (Р
ЗАД
).
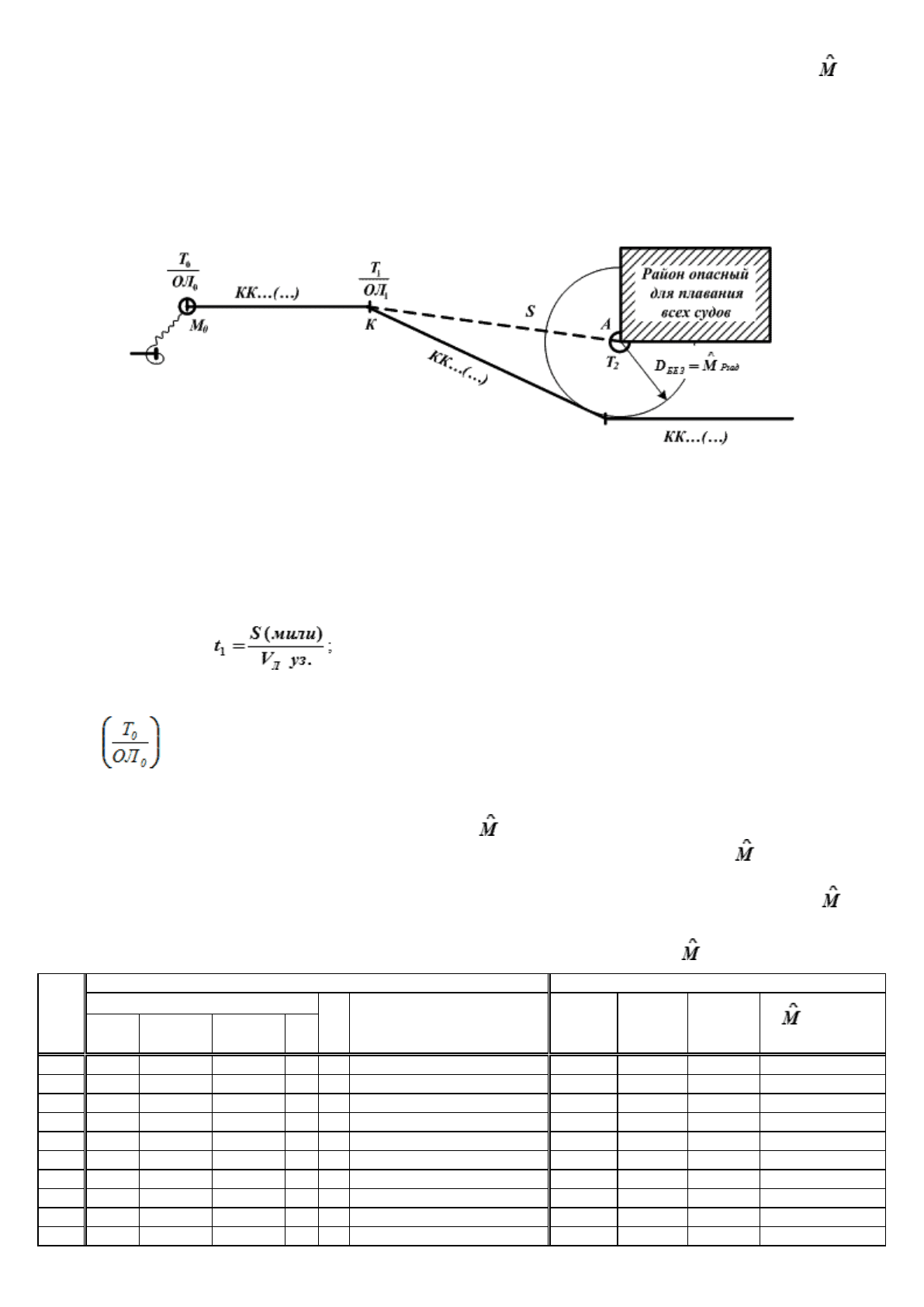
Рассмотрим это на примере (рис. 18.15).
Рис. 18.15. Выбор безопасного пути судна с учетом точности его плавания
Задача: исключить вхождение в «Район опасный для плавания всех судов» с Р
ЗАД
.
Для решения этой задачи необходимо:
1. → исходную (упреждающую) точку, в которой будет изменен курс судна (т. К), соединить с
навигационной опасностью (т. А);
2. → снять расстояние (S) между этими точками (т. К и т. А);
3. → рассчитать, сколько потребуется времени, чтобы судно прошло это расстояние с заданной
скоростью →
4. → рассчитать судовое время «прихода» в т. А → Т
2
= Т
1
+ t
1
;
5. → рассчитать время плавания по счислению t = Т
2
– Т
0
(последний расчет СКП (М
0
) был в т.
);
6. → по формуле (18.9) или (18.10) по К
С
и t рассчитать М
Сt
;
7. → по формуле (18.22) рассчитать М
СЧ
;
8. → по формуле (18.23) по М
СЧ
и Р
ЗАД
рассчитать
СЧ
;
9. → от т. А (навигационной опасности) провести дугу окружности радиусом R =
СЧ
РЗАД
= D
БЕЗ
;
10. → из исходной точки (т. К) провести касательную к данной дуге и снять ее направление –
искомая линия пути, следуя по которой судно пройдет навигационную опасность в D
БЕЗ
=
Р
ЗАД
.
18.6.3. Задачи по расчету точности места судна (М
0
, М
Сt
, М
СЧ
,
СЧ
с Р
ЗАД
)
№
зад.
Условие
Ответ
для расчета М
0
по 2-м ЛП
К
С
Время на которое
рассчитывается М
СЧ
М
0
(мили)
М
Сt
(мили)
М
СЧ
(мили)
СЧ
для Р =
95% (мили)
Т
0
(час)
m
ЛП1
(мили)
m
ЛП2
(мили)
θ°
1
09.00
± 0,2
± 0,9
30°
0,5
12.00
1,84
0,87
2,04
3,53
2
10.00
± 0,3
± 0,8
35°
0,6
12.00
1,49
0,84
1,71
2,96
3
11.00
± 0,4
± 0,7
40°
0,7
12.00
1,26
0,49
1,35
2,34
4
12.00
± 0,5
± 0,6
45°
0,8
16.00
1,10
1,60
1,94
3,36
5
13.00
± 0,6
± 0,5
50°
0,9
16.00
1,01
1,56
1,86
3,22
6
14.00
± 0,7
± 0,4
55°
1,1
16.00
0,98
1,54
1,83
3,17
7
15.00
± 0,8
± 0,3
60°
1,2
16.00
0,98
0,84
1,29
2,23
8
16.00
± 0,9
± 0,2
65°
1,3
20.00
1,01
2,60
2,79
4,83
9
17.00
± 0,8
± 0,3
70°
1,4
20.00
0,91
2,42
2,59
4,48
10
18.00
± 0,7
± 0,4
75°
1,5
20.00
0,83
2,10
2,26
3,91

Выводы
1. Любой измеренный навигационный параметр есть величина случайная и лишь с какой-то
степенью достоверности соответствующая его истинному значению.
2. Все погрешности измерений делятся на 3 вида:
• случайные;
• систематические;
• грубые (промахи).
3. Случайные погрешности подчиняются закону нормального распределения (закону Гаусса).
4. Основной характеристикой оценки точности измерения навигационного параметра является СКП
– средняя квадратическая погрешность.
5. Точность счислимого места принято оценивать радиальной или круговой СКП (М
СЧ
).
6. Вероятность нахождения счислимого места судна в круге, радиусом R = M составляет 0,63÷0,68
(63÷68%).
7. Коэффициент точности счисления (К
С
) характеризует скорость нарастания погрешности
счисления по времени плавания по счислению.
8. Вероятнейшее значение навигационного параметра (U
В
) соответствующего данной линии
положения (навигационной изолинии), находится в полосе ±m
ЛП
с вероятностью Р = 0,68 (68%).
9. Радиальная (круговая) СКП обсервованного места судна (М
0
) построена на полуосях эллипса
погрешностей, а ее величина определяется по формуле:
(мили)
10. Погрешность счислимого (текущего) места судна складывается квадратически из погрешности
исходной точки и погрешности счисления за время плавания от исходной точки до счислимого
(текущего) места.
11. Учет погрешности счислимого (текущего) места судна – одна из важнейших гарантий его
безопасного плавания.

ГЛАВА 19. ОПРЕДЕЛЕНИЕ МЕСТА СУДНА ПО РАДИОПЕЛЕНГАМ НА
КРУГОВЫЕ РАДИОМАЯКИ
19.1. Принцип радиопеленгования
Для решения задачи определения места судна в море по радиопеленгам на береговые радиомаяки
необходимы, как минимум, два условия:
• → наличие на берегу двух (или более) морских радиомаяков кругового излучения (КРМК),
находящихся в зоне плавания судна;
• → наличие радиопеленгатора на судне.
Радиопеленгатор → судовой прибор, предназначенный для определения направления на
источники излучения электромагнитных колебаний (КРМ
К
).
Современные судовые радиопеленгаторы можно классифицировать по способу индикации
искомого направления на радиомаяк и по способу его работы.
По способу индикации искомого направления судовые радиопеленгаторы разделяются на
слуховые и визуальные.
В слуховых радиопеленгаторах направление определяется на слух по громкости принимаемого
сигнала. Они могут быть с поворотной или неподвижной рамочной антенной. В радиопеленгаторах с
неподвижной рамочной антеной применяется гониометрическое устройство. К слуховым РП можно
отнести радиопеленгаторы типа «Рыбка», «Баркас».
В визуальных радиопеленгаторах для индикации направления применяются стрелочные
индикаторы (АРП) и электронно-лучевые трубки («Румб»).
По способу работы радиопеленгаторы делятся на неавтоматические и автоматические (АРП).
В современных судовых радиопеленгаторах применяется равносигнальный способ определения
направления и способ пеленгования по минимуму принимаемого сигнала.
Основные тактико-технологические характеристики судовых радиопеленгаторов приведены в
таблице 19.1.
Основные тактико-технологические характеристики радиопеленгаторов
Таблица 19.1.
Характеристика
АРП-50 (50Р, 53,
53Р, 85)
АРП-58 СВ ДВРП «Румб»
Диапазон частот (кГц) 187,5 ÷ 750,0 120 ÷1340
250 ÷ 545
1600 ÷ 2800
Точность
радиопеленгования (СКП):
– в автоматическом режиме
– в слуховом режиме
± 1,0° ÷ ± 1,5°
± 0,75° ÷ ± 1,0°
± 2,0°
± 1,5°
± 1,0°
–
Электропитание 127В, 50Гц
400-500 кГц, 115(220) В
и пост. 24В
127 (220)В, 50Гц
Особенности конструкции Гониометр Поворотная рамка
2-х канальный с
коммутацией каналов
Морской радиомаяк → устройство, имеющее фиксированное, известное мореплавателю,
положение и передающее специальные радиосигналы в определенном порядке и по определенному
расписанию и на известной мореплавателю частоте.
Морской радиомаяк кругового излучения (КРМ
К
) снабжен антенными устройствами, создающими
во всех направлениях по горизонту на равных удалениях одинаковую напряженность
электромагнитного поля, что и позволяет пеленговать его с помощью судового радиопеленгатора (РП),
обладающего свойством направленного приема, то есть определять направление на источник излучения
(КРМ
К
).
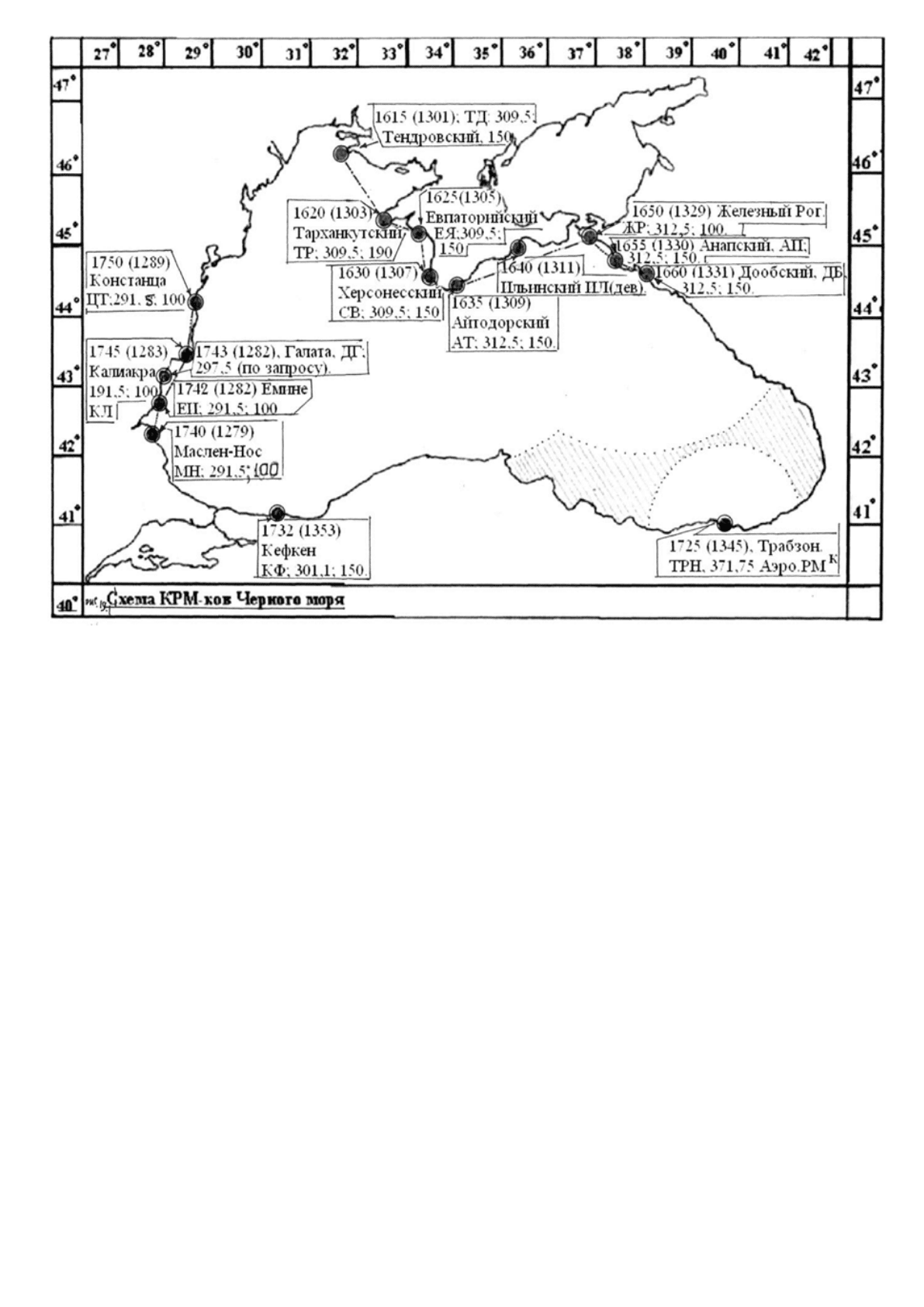
Рис. 19.1. Схема КРМ-ков Черного моря
КРМ-ки работают в диапазоне частот 285-325 кГц (длина волны 1056-936м) колебаниями класса
А1А или А2А.
Для улучшения условий использования и уменьшения взаимных помех КРМ-ки объединяются в
группы по 2-6 маяков в каждой и работают на излучение поочередно по расписанию на одной несущей
частоте (длине волны), а их сигналы отличаются друг от друга только позывными и частотой тона
(тональной модуляции). Такой порядок работы позволяет получать направления на несколько КРМ-ков,
не перестраивая радиопеленгатор на другую частоту.
Необходимая информация о морских радиомаяках и аэрорадиомаяках приведена в навигационном
руководстве «Радиотехнические средства навигационного оборудования (РТСНО)».
Для Северного Ледовитого и Атлантического океанов → см. отдел III «РТСНО» Адм. № 3001 (с.
67÷156).
На побережье Мирового океана установлено более 1.000 радиомаяков и аэрорадиомаяков, которые
могут использоваться судоводителями для определения по ним своего места в море.
Для Черного моря на рис. 19.1 «Схема КРМ-ков» приведена информация о радиомаяках и
аэрорадиомаяках (российский и международный номер, название, позывной, рабочая частота, дальность
действия).
Только незначительная часть акватории Черного моря (на рис. 19.1. заштрихована) не охвачена
рабочими зонами действующих радиомаяков.
Радиопеленгование → процесс определения направления распространения электромагнитной
волны (ЭМВ) от радиомаяка на судне (определение направления на передающую радиостанцию
радиотехническим методом).
Типовой судовой автоматический радиопеленгатор (АРП) работает в двух режимах: 1. ⇒ слуховой
и 2. ⇒автоматический.
При слуховом радиопеленговании направление на КРМ
К
определяется по интенсивности
слышимости принимаемого радиосигнала (по его «минимуму»).
В автоматическом режиме направление на КРМ
К
определяется автоматически после настройки
АРП на частоту КРМ
КА
.
