Муравченко В.Б., Ковалев С.А., Коннова С.С. Безапасность жизнедеятельности

Подождите немного. Документ загружается.

361

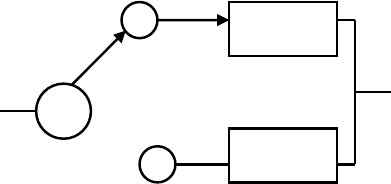
Рис.2.7.Системасненагруженнымрезервом

Переключатель А может представлять собой автоматический

датчик либо просто условно означать, что оператор заменяет эле-

мент 2 элементом 1.

В системе с распределением нагрузки по параллельным эле-

ментам при появлении отказа увеличивается интенсивность отка-

зов элементов, продолжающих работать. Примером системы с рас-

пределением нагрузки по параллельным элементам является креп-

ление автомобильного колеса; если какая-либо га

йка ослабляется,

то остальные гайки должны выдерживать большую нагрузку.

Еще одной формой резервирования является система «m» из

«n». В такой системе имеется n параллельно соединенных элемен-

тов, однако для того, чтобы система продолжала работать безот-

казно, должны сохранять работоспособность не менее m элементов.

Примером такой формы резервирования являются канаты висячего

моста, когда для того, чт

обы держать это сооружение, необходимо

некоторое минимальное число таких канатов.

Вероятность безотказной работы системы «m» из «n» имеет

вид:

()

−

−⋅⋅=

∑

PPCP , (2.8)

где Р

– вероятность безотказной работы i-гo количества элементов

(предполагается, что вероятность безотказной работы всех элемен-

тов одинакова);

C – число комбинаций.

В случае элементов с неодинаковой надежностью может ис-

пользоваться простой перебор всех вариантов.

362

2.4.3.Комбинированноесоединениеэлементоввсистеме

Простые комбинации подсистем с параллельным и последо-

вательным соединениями элементов можно легко проанализиро-

вать путем последовательного объединения подсистем в группу

параллельно или последовательно соединенных эквивалентных

элементов. Рассмотрим в качестве примера последовательное со-

единение подсистем с параллельными элементами, изображенное

на рис. 2.8.

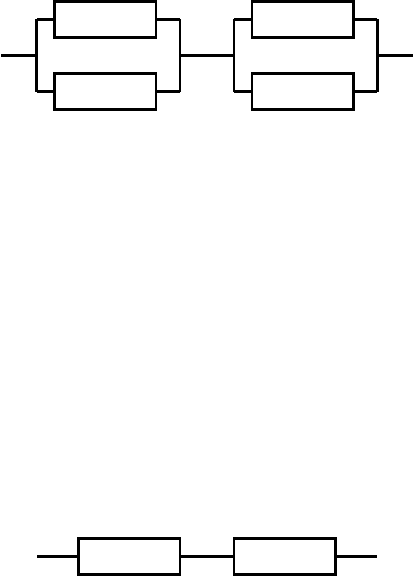
Рис.2.8.Системаспоследовательнопараллельнымсоединениемэлементов

Для вычисления безотказности этой системы вначале объе-

диняют параллельно соединенные элементы подсистем и рас-

сматривают последовательное соединение эквивалентных соеди-

нений. Допустим, что известны вероятности безотказной работы

этих элементов, т. е. известны показатели надежности элементов:

Р(А) = 0,9; Р(В) = 0,8; Р(С) = 0,7 и Р(Д) = 0,6. Тогда вероятность

безотказной работы параллельно соединенных элементов в под-

системах:

Р(АВ) = 1 – [1 – Р(А)]

· [1 – Р(В)] = 1 – 0,1 · 0,2 = 0,98;

Р(СД) = 1 – 0,3 · 0,4 = 0,88.

Далее определяем вероятность безотказной работы всей сис-

темы как последовательно соединенных подсистем или эквива-

лентных элементов (рис. 2.9).

АВ СД

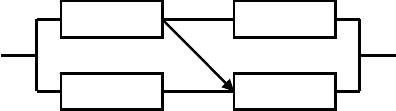
Рис.2.9.Системаспоследовательнымсоединениемэквивалентных

элементов(подсистем)

Вторая система показана на рис 2.10, где подсистемы с по-

следовательным соединением элементов соединены параллельно.

363

Рис.2.10.Системаспараллельнопоследовательнымсоединениемэлементов

В данном случае методика преобразования состоит в том, что

вначале объединяются последовательно соединенные элементы

подсистем, а затем рассматриваются параллельно соединенные эк-

вивалентные элементы. Предположим, что в данном случае эле-

менты имеют такую же надежность, как и в предыдущем примере.

Таким образом, вероятность безотказной работы последовательно

соединенных элементов в подсистемах:

Р(АС) = Р(А) · Р(С) = 0,9

· 0,7 = 0,63;

Р(ВД) = 0,8 · 0,6 = 0,48.

Следовательно, вероятность безотказной работы системы

(система представлена на рис 2.10 как система с параллельно со-

единенными эквивалентными элементами или подсистемами):

Р = 1 – [1 – Р(АС)] · [1 – Р(ВД)] = 1 – 0,37 · 0,52 = 0,8076.

Заметим, что различия в значениях вероятности безотказной

работы систем обусловлено различным соединением подсистем.

При рассмотрении комбинаций последовательно и параллель-

но с

оединенных элементов применимы прямые методы вычислений,

используемые в случае простых систем с последовательным и па-

раллельным соединениями элементов. Таким образом, для анализа

систем с комбинациями последовательных и параллельных соедине-

ний элементов основные формулы применяются последовательно.

АС

ВД

Рис.2.11.Системаспараллельнымсоединениемэквивалентныхэлементов

(подсистем)

364

2.4.4.Системысосложнымсоединениемэлементов

На практике встречаются системы, для описания которых па-

раллельное или последовательное соединение элементов не годит-

ся. Рассмотрим в качестве примера систему, изображенную на

рис. 2.12.

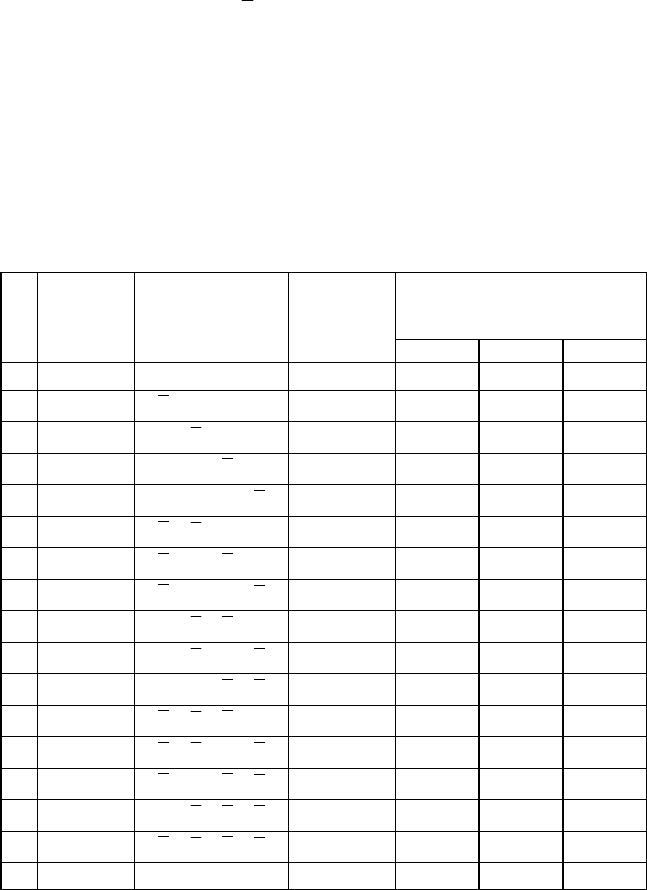
Рис.2.12.Системасосложнымсоединениемэлементов

Примером системы со сложным соединением элементов мо-

жет быть дорожная сеть, соединение энергетических систем и др.

В системе, изображенной на рис. 2.12, отказ элемента А на-

рушает сразу два пути АС и АД. Таким образом, это соединение не

является параллельным. Последовательным такое соединение на-

звать также нельзя, в случае отказа элемента С систем

а остается

работоспособной.

Для определения вероятности безотказной работы системы

или надежности функционирования системы используют несколь-

ко методов. В данном пособии рассмотрен самый простой метод.

С помощью этого метода можно определить надежность работы

любого типа технических систем, он легко поддается проверке и,

главное, позволяет рассмотреть влияние отказов элементов на ра-

боту систем

ы, т. е. на устойчивость функционирования системы.

Недостатком данного метода является громоздкость и трудность в

составлении универсальной программы для применения вычисли-

тельной техники.

Метод состоит в том, что рассматриваются все возможные

способы появления отказов, т. е. не отказал ни один элемент, отка-

зал один элемент, два и т. д.

Рассмотрим систему, изображ

енную на рис 2.12, и предпо-

ложим, что в данном случае элементы системы имеют такую же

вероятность безотказной работы, как и в предыдущем примере.

365

Определим А как событие, состоящее в том, что элемент А ра-

ботает безотказно, тогда

А – событие, состоящее в том, что элемент

А отказал. Аналогично определим событие для всех остальных эле-

ментов. Затем вычислим вероятность состояния системы для каждо-

го способа появления отказа. Все вычисления запишем в табл. 2.1 и

для проверки данного метода сделаем отметку о состоянии не только

сложной системы, но и систем с последовательно-параллельным и

пар

аллельно-последовательным соединением элементов.

Таблица 2.1

Вероятность безотказной работы технических систем,

показанных на рис. 2.12, 2.10, 2.8

Отметка о

работоспособности

систем, изображенных на:

№

п/п

Число

отказав-

ших эле-

ментов

Событие,

характеризую-

щее состояние

системы

Вероят-

ность

состояния

системы

рис. 2.12 рис. 2.10 рис. 2.8

1 0

АВСД∩∩∩

0,3024 + + +

2 1

АВСД∩∩∩

0,0336 + + +

3 1

АВСД∩∩∩

0,0756 + +/– +

4 1

АВСД∩∩∩

0,1296 + + +

5 1

АВСД∩∩∩

0,2016 + + +

6 2

АВСД∩∩∩

0,0084 – – –

7 2

АВСД∩∩∩

0,0144 + + +

8 2

АВСД∩∩∩

0,0224 – – +

9 2

АВСД∩∩∩

0,0324 + – +

10 2

АВСД∩∩∩

0,0504 + – +

11 2

АВСД∩∩∩

0,0864 – – –

12 3

АВСД∩∩∩

0,0036 – – –

13 3

АВСД∩∩∩

0,0096 – – –

14 3

АВСД∩∩∩

0,0056 – – –

15 3

АВСД∩∩∩

0,0216 – – –

16 4

АВСД∩∩∩

0,0024 – – –

1,0000 0,8400 0,8076 0,8624

366

Первая строка табл. 2.1 заполняется следующим образом:

вначале предположим, что в системе не отказал ни один элемент,

это событие записывается:

АВСД∩∩∩. Вероятность этого со-

стояния системы:

P(0) = P(А) · Р(В) · Р(С) · Р(Д) = 0,9 · 0,8 · 0,7 · 0,6 = 0,3024.

В графах «отметка о работоспособности системы» ставим

знак «+», если система работоспособна, и знак «–», если неработо-

способна.

Вторая строка табл. 2.1 предполагает, что в системе отказал

один элемент (элемент А). Это событие записывается:

АВСД∩∩∩.

Вероятность такого состояния системы определяется следующим

образом:

P(1) = P(

А ) · Р(В) · Р(С) · Р(Д) = 0,1 · 0,8 · 0,7 · 0,6 = 0,0336,

где P(

А ) – вероятность отказа элемента A: P( А ) = 1 – Р(А); Р(А) –

вероятность безотказной работы элемента А; в данном случае все

системы, изображенные на рис. 2.12, 2.10, 2.8 работоспособны.

Остальные строчки табл. 2.1 заполняются аналогично, в

предположении, что отказали один, два, три и четыре элемента

системы.

Проверка количества комбинаций с различным числом отка-

завших элементов производится по формуле:

!( )!

−

mm n

, (2.9)

где:

– число комбинаций отказавших элементов «m по n»; m –

число отказавших элементов;

n – общее число элементов в системе.

Таким образом, система со сложным соединением элементов

(подсистем) имеет вероятность безотказной работы – 0,84.

Оценивая устойчивость функционирования технической сис-

темы, необходимо знать её поведение в будущем. Если бы системы

и объекты были безотказны то большинство проблем, связанных

с безопасностью, исчезло. Но все объекты, изделия и системы

не веч

ны, поэтому необходимо знать срок их безотказной работы

с целью исключения аварий, вызванных отказами.

367

2.4.5.Оценкабезотказности

техническихсистемсрезервом

Для достижения высокой надежности работы технических

систем конструктивные технологические и эксплутационные меро-

приятия могут оказаться недостаточными и тогда применяется ре-

зервирование. Особенно это относится к системам, для которых

повышение надежности элементов не позволяет достичь требуемой

безотказности системы.

Резервирование может быть:

– постоянное резервирование с нагруженным или горячим

резервом;

– резервирование замещением с ненагруженным или холод-

ным резервом;

– резервирование с резервом, работающим в облегченном

режиме.

Резервирование целесообразно применять при опасности

возникновения аварии.

При постоянном резервировании резервные элементы или

цепи подключают параллельно основным. Такая система работает

как система с параллельным соединением элементов. Вероятность

безотказной работы тако

й системы высокая, однако все элементы

включены в работу системы, что не всегда экономически выгодно.

Расчет безотказности системы ведется как для системы с парал-

лельным соединением элементов.

При резервировании замещением резервные элементы вклю-

чаются только при отказе основных. Это включение может произ-

водиться автоматически или вручную.

Пример. Определить безотказность системы, состоящей из

двух последовательно-соединенных элементов, и безотказность

этой системы с одним резервным элементом. Элементы системы

взаимозаменяемы. Вероятность безотказной работы элементов из-

вестна: Р(А) = 0,9; Р(В) = 0,8; P(R) = 0,95.

Схема изображена на рис. 2.13.

368

Резерв

Рис.2.13.Схемадляопределениябезотказнойработы

системысрезервнымэлементом

Решение. Вероятность безотказной работы системы без ре-

зерва Р = Р(А) · Р(В) = 0,9 · 0,8 = 0,72.

Для определения вероятности безотказности системы необ-

ходимо рассмотреть все возможные состояния системы. Опреде-

лить вероятность каждого состояния системы, затем значения ве-

роятностей, при которых система работоспособна, сложить, и это

будет вероятность безотказной работы системы (в данном случае

оценка безотказности сис

темы проводится таким же методом, как и

для сложных систем). Вычисления запишем в табл. 2.2.

Таблица 2.2

Значения вероятностей состояния системы

№

п/п

Состояние

системы

Вероятность

Отметка

о работоспособном

состоянии

АВR∩∩

0,9 · 0,8 · 0,95 = 0,684 +

АВR∩∩

0,1 · 0,8 · 0,95 = 0,076 +

АВR∩∩

0,9 · 0,2 · 0,95 = 0,171 +

АВR∩∩

0,9 · 0,8 · 0,05 = 0,36 +

АВR∩∩

0,1 · 0,2 · 0,95 = 0,019 –

АВR∩∩

0,1 · 0,8 · 0,05 = 0,004 –

АВR∩∩

0,9 · 0,2 · 0,05 = 0,009 –

АВR∩∩

0,1 · 0,2 · 0,05 = 0,001 –

Σ = 1,00 0,967

Таким образом, вероятность безотказной работы системы,

состоящей из двух последовательно соединенных элементов и од-

ним резервным, равна 0,967.

369

В принципе, данным методом можно определить вероятность

безотказной работы любой технической системы с любым возмож-

ным подключением резерва, однако это требует довольно громозд-

ких вычислений, правильность которых легко проверяется.

Таким образом, количественная оценка вероятности отказа

системы требует довольно сложной работы, особенно систем, со-

стоящих из большого количества элементов.

Рассмотренный метод оценки бе

зопасности системы можно

назвать индуктивным. При анализе математической модели внача-

ле вычисляют вероятности состояний системы при всех возможных

отказах элементов системы, затем определяют влияние отказа каж-

дого элемента или комбинации элементов на работоспособность

системы. При таком подходе случайный пропуск неработоспособ-

ных состояний системы маловероятен. Однако метод очень трудо-

емок, приходится рассматривать вс

е возможные варианты.

При дедуктивном методе оценки безотказности системы соз-

дание математической модели начинают с выделения одного или

нескольких наиболее опасных неработоспособных состояний сис-

темы. Переход в каждое из этих состояний, т. е. опасный отказ сис-

темы, считается завершающим (главным) событием, которое воз-

никает в результате появления определенных сочетаний первичных

событий – отказов отдель

ных элементов, неправильных действий

людей и т. д. Условия, при которых возникает рассматриваемое

завершающее событие (опасный отказ системы), сводят в логиче-

скую схему, изображаемую в виде ориентированного графа с вет-

вящейся структурой – «дерево отказов».

370

3.Определениестепениповрежденияобъекта,

пострадавшеговчрезвычайнойситуации

3.1.Организацияработыпообследованиютехнического

состоянияобъектов,пострадавшихвчрезвычайнойситуации

Основные положения и порядок проведения обследования

технического состояния объектов, пострадавших в результате чрез-

вычайных ситуаций, отражены в следующем нормативном доку-

менте: Приказ от 02.08.2002 г. № 167 Государственного комитета

РФ по строительству и жилищно-коммунальному комплексу «Об

утверждении порядка проведения обследования технического со-

стояния объектов, пострадавших в результате чрезвычайных си-

туаций».

Обследование технического состояния объекто

в, пострадав-

ших в чрезвычайной ситуации, производится специалистами Феде-

рального агентства по строительству и жилищно-коммунальному

хозяйству (Росстрой) в присутствии (если это возможно) собствен-

ника (владельца) объекта.

Виды объектов, подлежащих обследованию, указываются в

решении Министерства регионального развития Российской Феде-

рации, куда входит Росстрой.

На основании представленных органами местного само-

управления, органами и

сполнительной власти субъекта РФ, ока-

завшихся в зонах чрезвычайных ситуаций, предварительных дан-

ных и схемы расположения объектов на соответствующей террито-

рии, комиссия Росстроя проводит обследования пострадавших объ-

ектов, в ходе которого выявляет техническое состояние конструк-

тивных элементов объекта, в том числе скрытых, и определяют

степень их повреждения.

По результатам обследо

вания составляется акт в двух экзем-

плярах. Акты подписываются руководителем группы (комиссии),

производившей обследование и собственником (владельцем) объ-

екта, если последний присутствовал при обследовании объекта.

Один экземпляр акта остается в деле комиссии Росстроя, второй

экземпляр передается межведомственной комиссии.