Назаров Х.Н. Робототехнические системы и комплексы
Подождите немного. Документ загружается.

21
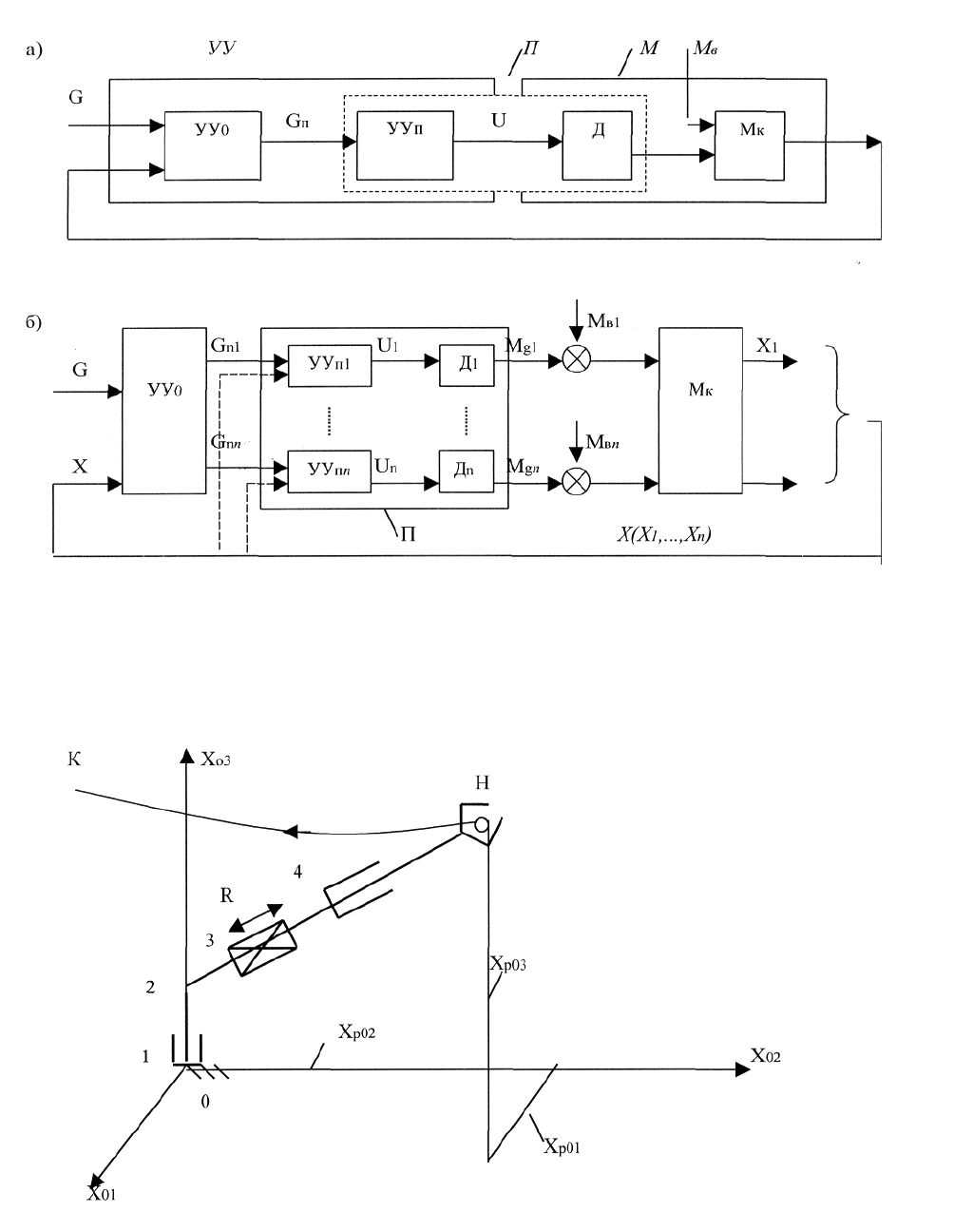
Рис. 2.1 Функциональная схема системы управления робота:
а – общая схема системы управления робота; б – схема системы программного
управления роботом.
Рис. 2.2 Перевод рабочего органа робота с одной точки в другую.
В простейшем случае G(t) задание может заключаться в переводе рабочего
органа из одной точки рабочей зоны манипулятора в другую (рис.2.2). Примером
более сложного задания является перемещение рабочего органа по определенной

22
траектории. При этом может быть задана и определенная ориентация рабочего
органа в пространстве [2].
Качество отработки заданий оценивается с помощью критериев качества,
которые выбираются исходя из конкретных требований к данному роботу. В
частности, такими критериями могут быть точность отработки задания,
быстродействие, расход энергии и т. п.
Целью рассмотрения системы управления может быть
решение одной из двух
задач -задачи анализа системы или задачи ее синтеза. В первом случае даются
система и значения всех ее параметров, и требуется определить ее свойства. Во
втором случае, наоборот, задаются свойства, которыми должна обладать система,
т.е. требования к ней, и необходимо создать систему, удовлетворяющую этим
требованиям.
В
обоих случаях обязательным этапом исследования является математическое
описание системы, т. е. получение ее математической модели.
2.2. Математическое описание частей системы управления роботом
Для получения математического описания системы необходимо прежде всего
составить математическое описание всех частей ее функциональной схемы. В
соответствии со схемой рис.2.1 система управления манипулятором робота в самом
общем виде описывается зависимостью
где A-оператор систем, определяющий математические операции, с помощью
которых по функциям G(t) и M
в
(t) может быть найдена функция X(t).
Оператор А может быть задан в виде уравнений, графиков, таблиц.
Зависимость (2.1) получается из математического описания двух основных
частей системы-объекта управления (манипулятора) и устройства управления, т. е.
из системы
где Ам и Ауу - операторы манипулятора и устройства управления
соответственно.
В свою очередь, согласно рис.2.1а, каждую из этих зависимостей можно
разбить на две и представить выражение (2.1) в виде совокупности следующих
четырех
зависимостей:
Первые два выражения описывают манипулятор, а последние два - устройство
управления. Соответственно здесь Амк, Ад, Аууп, Aо - операторы механической
части манипулятора (без двигателей), собственно двигателей, устройства
управления приводов и общей части устройство управления всего манипулятора.
(2.1)
(2.2)
(2.3)

23
Из всех этих зависимостей особое значение имеет первая, представляющая
математическое описание кинематической части манипулятора, так как оно является
специфическим именно для робототехники. Получение описаний остальных частей
системы управления-приводов и устройств управления осуществляется по
правилам, изложенным в общих курсах теории автоматического управления,
приводов, устройств автоматики и вычислительной техники.
Так, в линейном приближении последние зависимости могут быть, например,
выражены следующим образом с помощью передаточных функций:
Здесь Wn(p)- передаточная матрица приводов, связывающая их движущие
моменты Мд с управляющим воздействием на их входе Gn; W
01
(p) - передаточная
матрица последовательной части устройства управления манипулятором; W
02
(p) -
передаточная матрица части устройства управления, реализующая динамическую
коррекцию с помощью обратных связей по выходным переменным X; X
3
=G -
задающее воздействие в виде подлежащей отработке выходной переменной как
функции времени; р - оператор дифференцирования по времени.
2.3. Математическое описание механической части манипулятора робота
Рассмотрим вывод уравнений механической части манипулятора. Выходные
переменные манипулятора - это координаты всех его степеней подвижности X1,...,
Xn, где п- число степеней подвижности. Их значения определяют положение
манипулятора в пространстве, включая его рабочий орган. Входными
воздействиями на манипулятор являются движущие моменты (усилия) двигателей
Mд1..., Mдn (будем полагать, что число двигателей равно числу степеней
подвижности) и различные возмущающие моменты (усилия), приведенные к выходу
двигателей.
В статике, когда эти моменты взаимно уравновешены, манипулятор
неподвижен. В этом режиме он описывается алгебраическими уравнениями статики,
которые связывают временные переменные и определяются конструкцией
манипулятора.
Например, манипулятор, изображенный на рис.2.2, имеет 4 степени
подвижности - три угла поворота
ϕ
,
θ
,
γ
и одно поступательное перемещение R.
Это так называемые переносные степени подвижности манипулятора. Кроме того,
имеются еще ориентирующие степени подвижности его рабочего органа. В самом
общем случае их может быть три (три угла поворота). Эти степени подвижности, не
влияя на положение центра рабочего органа, определяют его ориентацию в
пространстве.
Уравнения манипулятора в статическом режиме обычно записываются
разрешенными относительно координат центра рабочего органа в прямоугольной
системе координат, неподвижной относительно основания манипулятора
(координаты Xpol, Xpo2, ХроЗ на рис.2.2), т. е. в виде
(2.4)
(2.5)
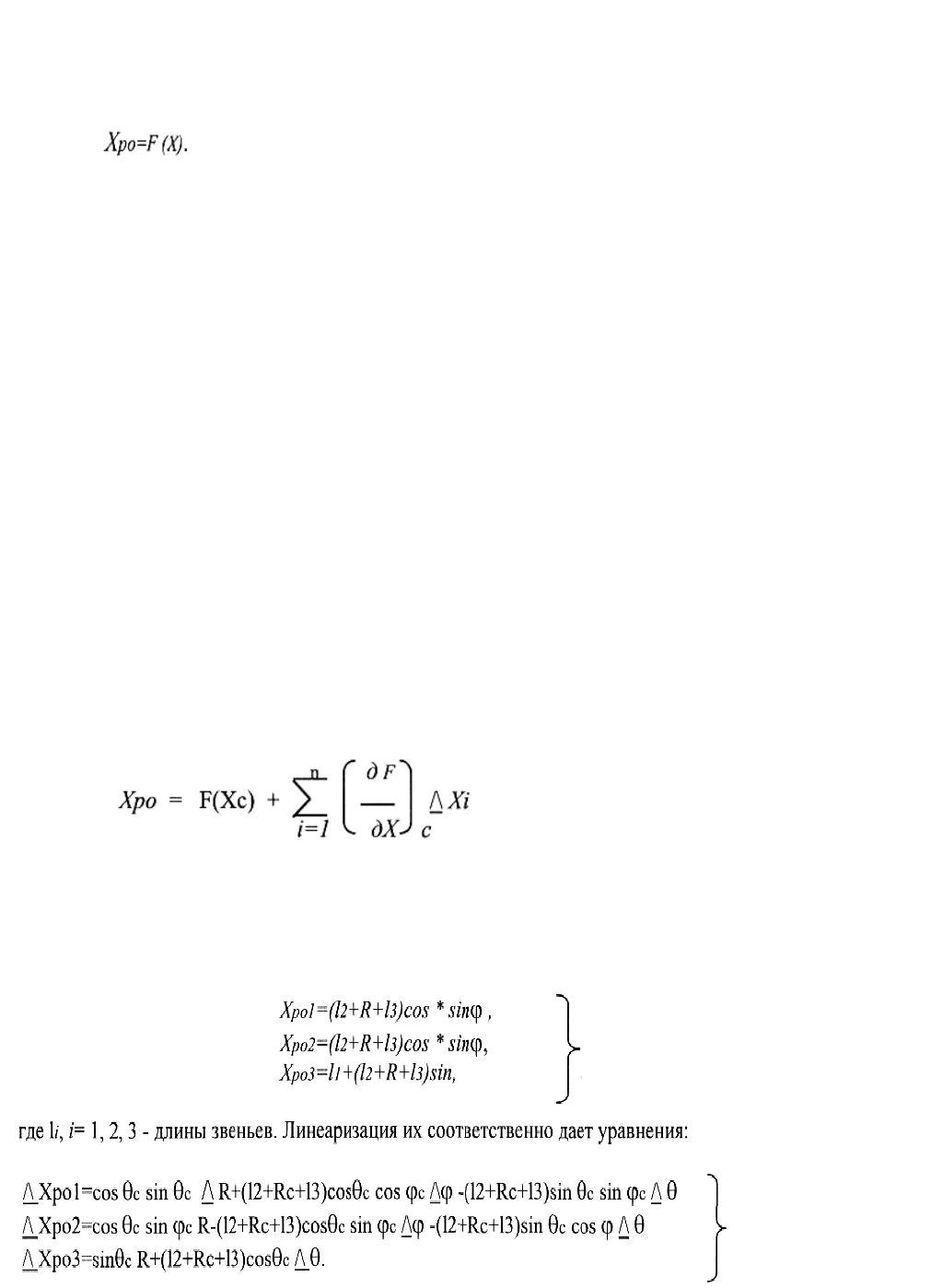
24
Здесь индекс «О» у Хро показывает, что эта переменная определена в системе
координат, связанной с основанием манипулятора. В общем виде уравнение (2.5)
можно записать так:
Здесь X-относительные координаты степеней подвижности манипулятора,
определяющие относительное положение звеньев манипулятора, которые образуют
кинематические пары, реализующие отдельные степени подвижности. Эти
координаты получили название обобщенных координат манипулятора.
В механике уравнение (2.6) называется уравнением кинематики
манипулятора, а его решение, т. е. нахождение декартовых координат рабочего
органа по обобщенным координатам манипулятора, прямой задачей кинематики
манипулятора. Соответственно нахождение значений обобщенных координат X по
декартовым координатам Хро называется обратной задачей кинематики
манипулятора.Уравнение (2.6) при необходимости может быть составлено не только
для рабочего органа, но и для любого промежуточного звена манипулятора.
Соответственно прямая задача кинематики манипулятора в общем случае относится
к любому его звену.
Уравнение типа (2.6) нелинейно, так как содержит тригонометрические
функции угловых координат. При рассмотрении малых отклонений
установившегося режима эти уравнения можно линеаризовать переходом к
приращениям переменных, как принято в теории автоматического управления. В
этом случае от уравнения (2.6) переходят к уравнению
Здесь индекс «с» означает, что значения переменных и производных функций
F(X) относятся к статическому режиму, относительно которого рассматриваются
отклонения.
Для 1 схемы манипулятора, показанной на рис.2.2, уравнения (2.6) имеют вид:
(2.6)
(2.7)
(2.8)
(2.9)

25
Рассмотрим теперь уравнения динамики механической части манипулятора.
Удобным средством для этого являются уравнения Лагранжа II рода:
Здесь L=T-П - функция Лагранжа, где П и Т - потенциальная и кинетическая
энергия рассматриваемого объекта, Xi и Xi -обобщенные координаты и их первые
производные (скорости), Мi - результирующий момент (усилие), действующий на
выходе i-го двигателя. Для механической части манипулятора в общем виде
уравнение Лагранжа принимает вид
где А - симметричная матрица (размерности nХn), а b(Х,Х)- вектор размерности n,
которые выражаются через геометрические параметры и массы звеньев
манипулятора.
Расчет этих величин представляет собой достаточно объемную задачу,
которая должна решаться на ЭВМ. Для ряда типовых кинематических схем
манипуляторов в литературе приводятся готовые программы для таких расчетов.
Уравнение (2.11) должно решаться совместно с уравнением «кинематики
манипулятора» (2.6), связывающего декартовые координаты манипулятора с его
обобщенными координатами. Таким образом, в целом математическое описание
механической части манипулятора, представленное в общем виде первой
зависимостью (2.3)
выражается системой уравнений (2.6) и (2.11).
Линеаризация уравнения (2.11) дает, естественно, дифференциальное
уравнение второго порядка, в котором при второй производной коэффициент
определяется моментами инерции механической системы манипулятора.
Для манипулятора, показанного на рис.2.2, уравнение (2.11) имеет вид:
Здесь q = r2m2 + (l2 + R + lз) m3; mi - масса звеньев, ri - расстояние от начала
звена до его центра масс; i= 1, 2, 3; g-ускорение свободного падения. Его
линеаризация в результате перехода к малым приращениям и пренебрежения
малыми членами дает уравнение:
(2.10)
(2.11)
(2.12)

26
Глава 3 . Робототехнические системы и комплексы
3.1. Классификация робототехнических систем и комплексов. Основные
типы робототехнических комплексов.
Технологические ячейки, участки, линии снабженные роботами называются
роботизированными технологическими комплексами (РТК) [12].
Разнообразие производственных процессов в машиностроении и
приборостроении определяют различные типы РТК.
Общая классификация РТК применительно к машиностроению приведена в
табл. 3.1.
Таблица 3.1
N Классификационный признак Наименование РТК
1. Тип роботизированного
подразделения
а) роботизированная
технологическая ячейка
б) роботизированный участок
в) роботизированная линия
г) для вновь создаваемого
производства
2. Характер изменения
производства, связанного с
созданием РТК
а) с принципиально новой
технологией;
б) с новым технологическим
оборудованием;
в) с новой компоновкой.
3. Вид роботизированного
технологического процесса
Механообработка, холодная
штамповка, литье, прессование,
сварка, сборка, контроль и
испытания.
(2.13)

27
4. Компоновка комплекса а) линейная;
б) круговая;
в) линейно-круговая;
г) по площади;
д) объемная
5. Тип управления а) централизованный;
б) децентрализованный;
в) комбинированный
6. Степень участия человека с участием человека в выполнении
технологических операций:
а) основных;
б) вспомогательных;
в) основных и вспомогательных
В управлении комплексом:
а) с автоматическим управлением;
б) с автоматизированным
управлением.
7. Структурный признак а) однопозиционные;
б) групповые;
в) многопозиционные.
Основные типы РТК.
Роботизированная технологическая ячейка (РТЯ) является простейшим типом
РТК. В ней выполняется минимум основных технологических операций. При этом
число единиц технологического оборудования (ТО) и ПР в составе РТК невелико. В
РТЯ может совсем отсутствовать ТО, когда основную операцию выполняет
непосредственно ПР.
Роботизированный технологический участок (РТУ). Он характеризуется
выполнением нескольких основных технологических операций, которые
объединены этим участком технологически, конструктивно (оборудованием) и
организационно (упорядоченность). Эти операции могут быть одинаковыми или
различными.
Если операции технологически связаны, такой комплекс представляет собой
роботизированную технологическую линию (РТЛ).
Простейший РТУ может включать несколько единиц технологического
оборудования, обслуживаемых одним ПР (ПР неподвижен, ТО размещается вокруг
него, либо ПР подвижен, перемещается вдоль ТО).
Более сложным является РТУ, выполненный из нескольких единиц ТО и
обслуживаемый одинаковыми ПР.
28
Компоновка комплекса
При линейной компоновке оборудование располагается в ряд (по линии), а
объемная компоновка означает его расположение на нескольких этажах.
В РТК различают следующие типы управления:
• централизованное управление осуществляется от стандартного
управляющего ЭВМ или от специального устройства управления;
• децентрализованное управление осуществляется с помощью
совокупности местных устройств управления, которые
связанны друг с
другом с целью взаимной координации. Например, увязка по времени
начала и конца отдельных операций;
• комбинированное управление предполагает наряду с централизованным
управлением наличие местных устройств управления. Такая система
управления может быть одноуровневой, когда сигналы управления,
поступающие из центра и сигналы местных УУ, комбинируются на
одном уровне; иерархической (многоуровневой
), когда местные УУ
подчинены центру.
Структурный признак отражает тип структуры РТК ( взаимодействие ПР и ТО
внутри комплекса). По этому признаку РТК бывают - однопозиционные РТК
(станок-робот, в комплекте с единицей ТО), групповые (один робот и несколько
однотипных или разнообразных ТО) и многопозиционные (группа роботов,
выполняющих взаимосвязанные и взаимодополняющие функции).
3.2. Основные схемы применения промышленных роботов в комплексах
В РТК используются следующие основные схемы применения ПР:
1. Единичное обслуживание оборудования.
1.1. Встраивание робота в оборудование.
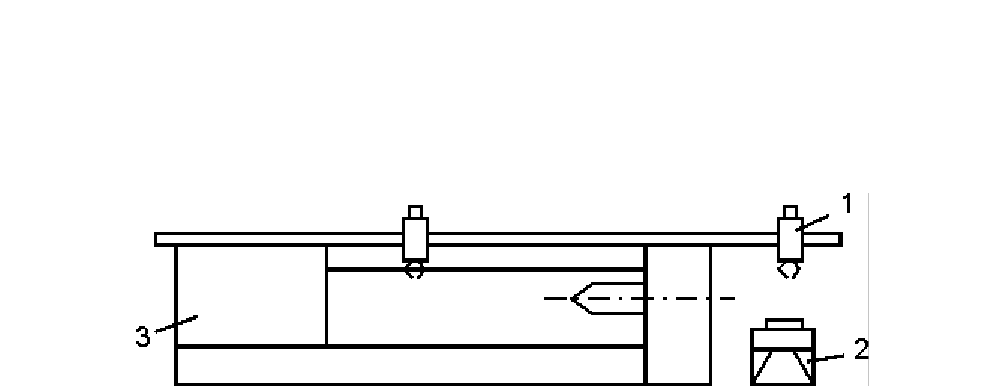
Рис.3.1. Робот встроен в оборудование: 1 - ПР; 2 - конвейер; 3 - основное
технологическое оборудование.
В РТК используется однопрограммный робот и система программного
управления общая для ПР и технологического оборудования, применяется в
массовом и крупно-серийном производстве. Необходима подача заготовки на
фиксированную загрузочную позицию.
1.2. Расположение ПР у основного ТО.
РТК имеет одно- или
многопрограммный ПР, общую или раздельную систему
программного управления (СПУ).
29
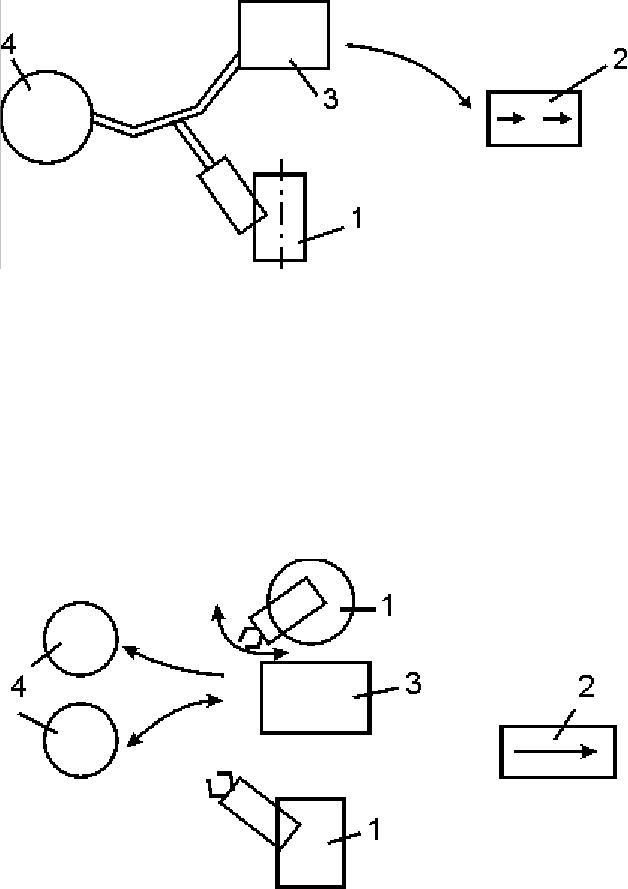
Рис.3.2. Расположения ПР у основного ТО: 1 - ПР; 2 - конвейер; 3 - основное
ТО; 4 - магазин с заготовками, деталями или инструментом.
Применяется в условиях крупносерийного и серийного производства.
Необходима подача заготовки на фиксированную позицию ( конвейерным и
трактовым магазином).
1.3. Обслуживание несколькими ПР группы машин, число которых меньше
числа ПР.
Рис.3.3. РТК с несколькими роботами.
Два или более ПР выполняют различные функции при обслуживании единицы
основного ТО. Имеют общую или раздельную СПУ. Обслуживают станочные
центры, кузнечно-прессовые машины и оборудование других видов.
2. Групповое обслуживание оборудования.
При этом производится обслуживание несколькими роботами группы
машин, число которых превышает число ПР.
2.1. Обработка деталей с постоянной последовательностью операций.
Однопрограммные ПР в составе автоматических линий с жесткой связью.
Необходима подача заготовки на фиксированную позицию. Возможна раскладка
обработанных деталей в тару. Передача деталей от одной позиции к другой
осуществляется конвейером или роботами.
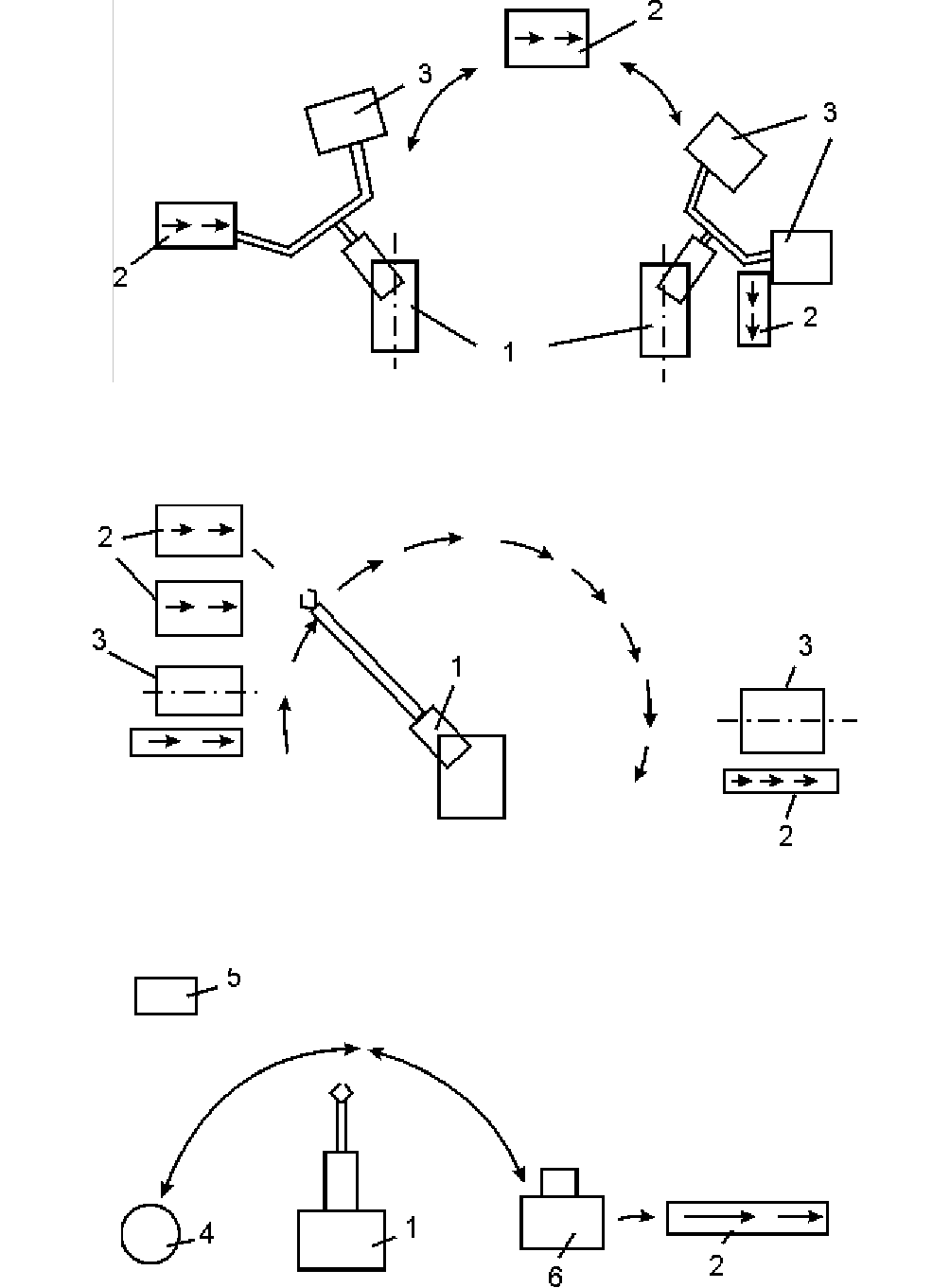
30
Рис.3.4. Групповое обслуживание оборудования промышленными роботами.
2.2. Круговое расположение оборудования (до 5 единиц).
Рис.3.5. Круговое расположение оборудования.
Обслуживание оборудования, работающего независимо или с жесткой
связью с многопрограммным или однопрограммным роботом соответственно.
3. Индивидуальное выполнение основных технологических операций.
Рис.3.6. Индивидуальное выполнение основных технологических операций.
Такие РТК имеют вспомогательное устройство (5), расширяющее функции ПР и
вспомогательное устройство (6) ориентации или фиксации (рис.3.6).
