Никишкин В.А., Малахов А.Н., Максюков Н.И. Высшая математика
Подождите немного. Документ загружается.


Вычисление интеграла
∫
udv
посредством применения формулы (1)
называют интегрированием по частям.
Примеры:
1
0
.
)1n( xdxlnxJ
n
−≠=
∫
u=lnx, dv=x
n
dx;
1n
x
v ,
x
dx
du
1n
+
==
+
C
1n
1
xln
1n
x
dxx
1n
1
xln
1n
x
J
1n
n
1n
+
+
−
+
=
+
−
+
=
++
∫
2
0
.
2
x
= v,
x+1
dx
=du xdx;=dv ,arctgxu ;xarctgxdx
2
2
==
∫
J
[
]
C
2
x
arctgx
2
1x
dx
x+1
1
2
1
dx
2
1
arctgx
2
x
dx
x1
1-)x+(1
2
1
arctgx
2
x
dx
x+1
x
2
1
arctgx
2
x
J
2
2
2
2
22
2
22
+−
+
=+−=
=
+
−=−=
∫
∫∫
3
0
.
∫
∫
∫
=−=== xdxsinx2xsinxxsindxxdxcosxJ
222
Еще раз применим формулу интегрирования по частям
Cxsin2xcosx2xsinxxcosxd2xsinx
22
+−+=+=
∫
4
0
.
xsinv ,dxedu ;xdxcosdv ,eu ;xdxcoseJ
xxx
=====
∫
∫
−= xdxsinexsineJ
xx
Еще раз применим формулу интегрирования по частям
xcosv ,dxedu ;xdxsindv ,eu
xx
−====
JxcosexsineJ
xx
−+=
Это равенство понимается как равенство множеств (т.е. как равенство
представителей множеств J и e
x
sinx+e
x
cosx-J) c точностью до произвольной
постоянной, поэтому отсюда получаем
Ce
2
xcosxsin
J
x
+
+
=
5
0
.
xv ,
xa
x
du ;dxdv ,xau ;dxxaJ
22
2222
=
−
−
==−=−=
∫
∫∫
−
+−=−=
22
2
2222
xa
dxx
xaxdxxaJ
Добавим и вычтем а
2
в числителе подынтегральной функции интеграла, стоящего
в правой части равенства; тогда, произведя деление на
22
xa −
, будем иметь
∫∫∫∫
−=−−
−
=
−
−−
=
−
J
a
x
arcsinadxxa
xa
dx
adx
xa
)xa(a
xa
dxx
222
22
2
22
222
22
2
Подставим это
выражение в формулу (2), получим
J
a
x
arcsinaxaxJ
222
−+−=
Отсюда
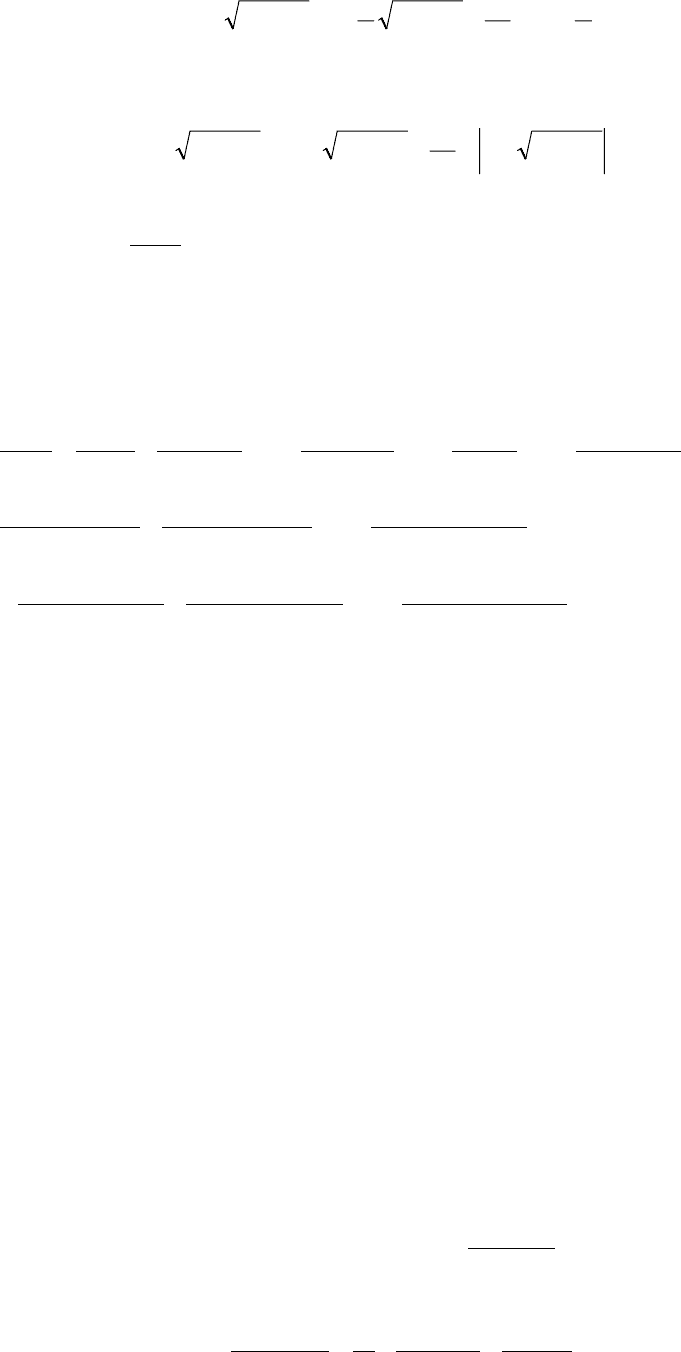
C
a
x
arcsin
2
a
xa
2
x
dxxaJ
2
2222
++−=−=
∫
6
0
. Проводя аналогичные вычисления, легко получить, что
Cxaxln
2
a
xaxdxxa
22
2
2222
+±+±±=±
∫
Теорема 3. Пусть
)x(Q
)x(P
- правильная рациональная дробь с вещественными
коэффициентами, знаменатель которой имеет вид:
n1m1
)qxpx(...)qxpx()bx(...)bx()x(Q
nn
2
11
2
m1
λλββ
++⋅⋅++−⋅⋅−=
Тогда для этой дроби справедливо следующее разложение на сумму простейших
дробей:
n
nn
1
11
m
m
1
1
)qxpx(
NM
...
)qxpx(
NM
)qxpx(
NM
...
)qxpx(
NM
...
)qxpx(
NM
)qxpx(
NM
)bx(
B
...
bx
B
...
)bx(
B
...
)bx(
B
bx
B
)x(Q
)x(P
nn
2
)n()n(
2
nn
2
)n(
2
)n(
2
nn
2
)n(
1
)n(
1
11
2
)1()1(
2
11
2
)1(
2
)1(
2
11
2
)1(
1
)1(
1
m
)m(
m
)m(
1
1
)1(
2
1
)1(
2
1
)1(
1
λ
λλ
λ
λλ
β
β
β
β
++
+
++
++
+
+
++
+
+
+
++
+
++
++
+
+
++
+
+
−
++
−
++
−
++
−
+
−
=
(1)
В этом разложении - некоторые вещественные
постоянные, часть которых может быть равна 0.
)n()n()1(
1
)1(
1
)m()1(
2
)1(
1
nnm
N,M,...,N,M,B,...,B,B
λλβ
Замечание. Для определения постоянных
в общем случае следует
привести равенство (1) к общему знаменателю и после этого сравнить
коэффициенты при одинаковых степенях в числителях. При этом, если степень
многочлена Q(x) равна l, то вообще говоря, в числителе правой части равенства
(1) после приведения к общему знаменателю получается многочлен степени l-1,
т.е. многочлен с l коэффициентами, число же неизвестных
также
равняется l.
)i(
j
)i(
j
)i(
j
B,N,M
)i(
j
)i(
j
)i(
j
B,N,M
Таким образом, мы получаем систему l уравнений с l неизвестными.
Существование у нее решения вытекает из доказанной теоремы.
Рассмотрим основные методы разложения на простейшие дроби.
6.6. Метод неопределенных коэффициентов
Найдем разложение на простейшие дроби для
)1x(x
1x
2
2
−
−
.
Общий вид разложения в этом случае
1x
EDx
)1x(
CBx
x
A
)1x(x
1x
22222
2
+
+
+
+
+
+=
+
−
Приводя к общему знаменателю и отбрасывая его, имеем
x
2
-1=A(x
2
+1)
2
+(Bx+C)x+(Dx+E)( x
2
+1)x
Приравняем коэффициенты при одинаковых степенях х:

при х
0
A=-1 Отсюда находим: A=-1
при х C+E=0 B=2
при х
2
2A+B+D=1 C=0
при х
3
E=0 D=1
при х
4
A+D=0 E=0 ,
поэтому искомое разложение имеет вид:
1x
x
)1x(
x2
x
1
)1x(x
1x
22222
2
+
+
+
+−=
+
−
6.7. Метод вычеркивания
Пусть знаменатель Q(x) правильной рациональной дроби
)x(Q
)x(P
имеет
вещественное число а корнем кратности
α. Тогда среди простейших дробей, на
сумму которых раскладывается дробь
)x(Q
)x(P
, есть дробь
α
)ax(
À
−
. По лемме 1
коэффициент
)a(
)a(P
À
ϕ
= , где
α
ϕ
)ax(
)x(Q
)x(
−
=
.
Правило: для вычисления коэффициента А при простейшей дроби
α
)ax(
À
−
,
соответствующей вещественному корню а многочлена Q(x) кратности
α, следует
вычеркнуть в знаменателе дроби
)x(Q
)x(P
скобку ( и в оставшемся выражении
положить х=а. Отметим, что этот прием применим лишь для вычисления
коэффициентов при старших степенях простейших дробей, соответствующих
вещественным корням Q(x).
α
)ax −
Метод вычеркивания особенно эффективен в случае, когда знаменатель
Q(x) имеет лишь однократные вещественные корни, т.е. когда Q(x)=(x-a
1
)(x-a
2
)⋅...
⋅(x-a
n
). Тогда справедливо представление
n
n
2
2
1
1
ax
A
...
ax
A
ax
A
)x(Q
)x(P
−
++
−
+
−
=
,
все коэффициенты которого могут быть вычислены по методу вычеркивания. Для
вычисления коэффициента А
к
следует вычеркнуть в знаменателе дроби
)x(Q
)x(P
скобку (х-а
к
) и в оставшемся выражении положить х=а
к
.
Найти разложение дроби
2x
A
1x
A
1x
A
)2x)(1x(
x
3
21
2
−
+
+
+
−
=
−−
3
2
1x
x
A
6
1
)3)(2(
1
)2x)(1x(
x
A
2
1
21
1
)1x)(2x(
x
A
2x
2
3
1x2
1x1
=
−
=
−=
−−
−
=
−−
=
−=
⋅−
=
+−
=
=
−=
=
Отсюда
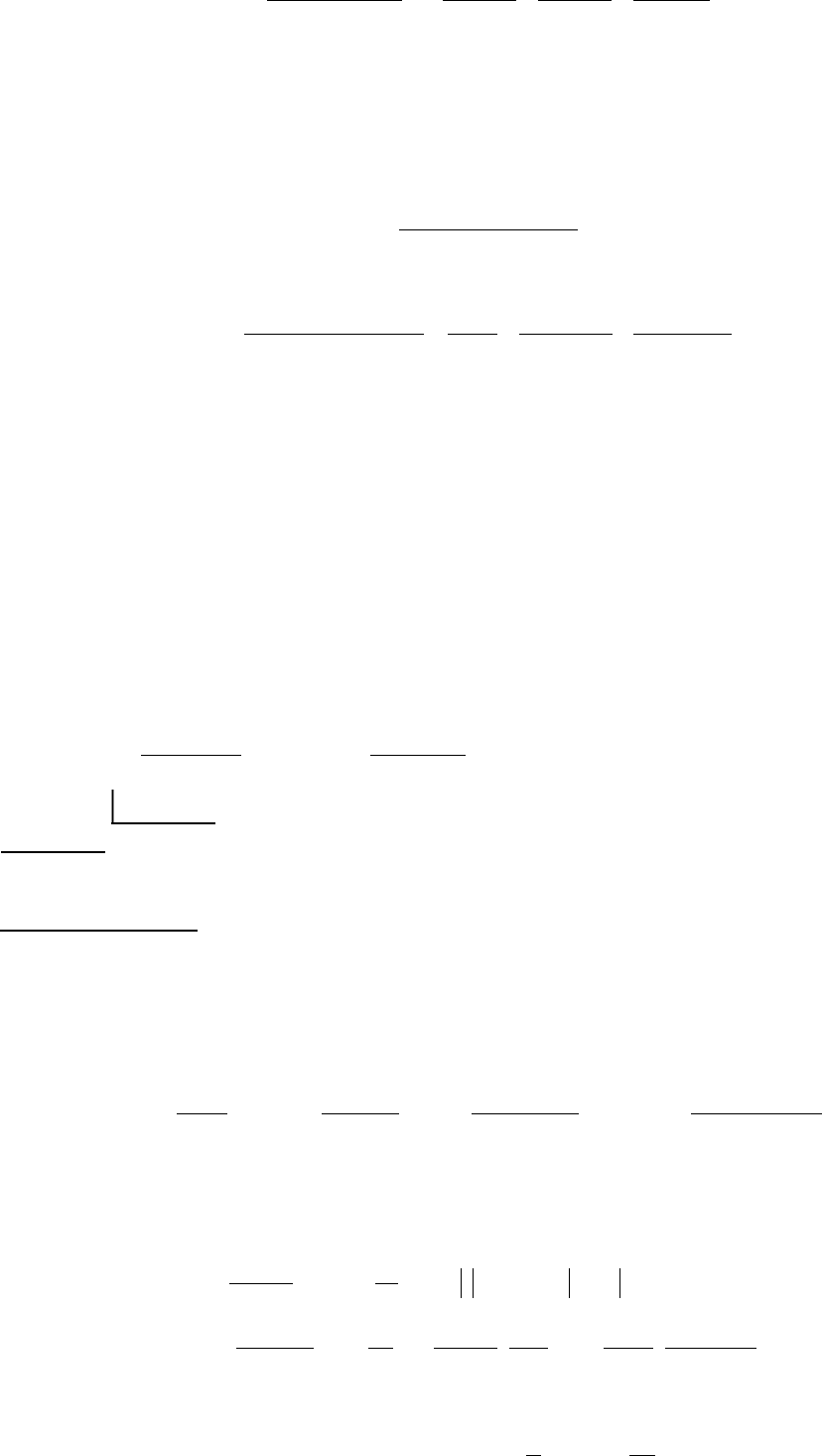
)2x(3
2
)1x(6
1
)1x(2
1
)2x)(1x(
x
2
−
+
+
−
−
−=
−−
Замечание. Метод вычеркивания снижает трудоемкость вычислений и в более
сложных случаях.
Разложить правильную дробь
22
234
)1x)(2x(
1x3x2x3
+−
−++
x
2
+1 имеет комплексные корни ⇒
22
22
2
11
22
234
)1x(
NxM
1x
NxM
2x
B
)1x)(2x(
1x3x2x3
+
+
+
+
+
+
−
=
+−
−++
Метод неопределенных коэффициентов приводит к системе 5-го порядка. Если же
В определить методом вычеркивания, то система будет уже только 4-го порядка.
6.8. Интегрирование некоторых классов функций
6.8.1. Интегрируемость рациональной дроби
Прежде всего отметим, что всякую неправильную рациональную дробь можно
(посредством деления числителя на знаменатель “уголком”) представить в виде
суммы алгебраического многочлена и правильной рациональной дроби.
Пример.
()
2xx
1x4
x2x
2xx
1xx
2
2
2
34
++
+
+−=
++
+−
x
4
- x
3
+ 1 x
2
+x+2
-
x
4
+x
3
+2x
2
x
2
- 2x
-2x
3
-2x
2
+1
-
-2x
3
-2x
2
-4x
Остаток 1+4х
Интегрировать многочлен мы умеем. В силу теоремы о разложении правильной
рациональной дроби с вещественными коэффициентами на простейшие, вопрос
сводится к интегрированию простейших дробей:
1.
b
x
B
−
II.
()
β
bx
B
−
III.
qpxx
NMx
2
++
+
IY.
()
λ
qpxx
N
2
++
+Mx
Здесь
β=2,3,...; λ=2,3,...; В, М, N, b, p, q - некоторые вещественные числа, причем
трехчлен х
2
+px+q не имеет вещественных корней, т.е.
p
2
-4q<0.
I.
()
()
∫∫
−=+−=+==
−
bxt cbxlnBctlnB
t
dt
Bdx
bx
B
II.
()
()
()
∫∫
+
−
⋅
−
=+⋅
−
−==
−
−
−
c
bx
1
1
B
c
t
1
1
B
t
dt
B
bx
B
1
1
β
ββ
β
ββ
Здесь t=x-b
III.
−+
+=++
4
p
q
2
p
xqpxx
2
2
2
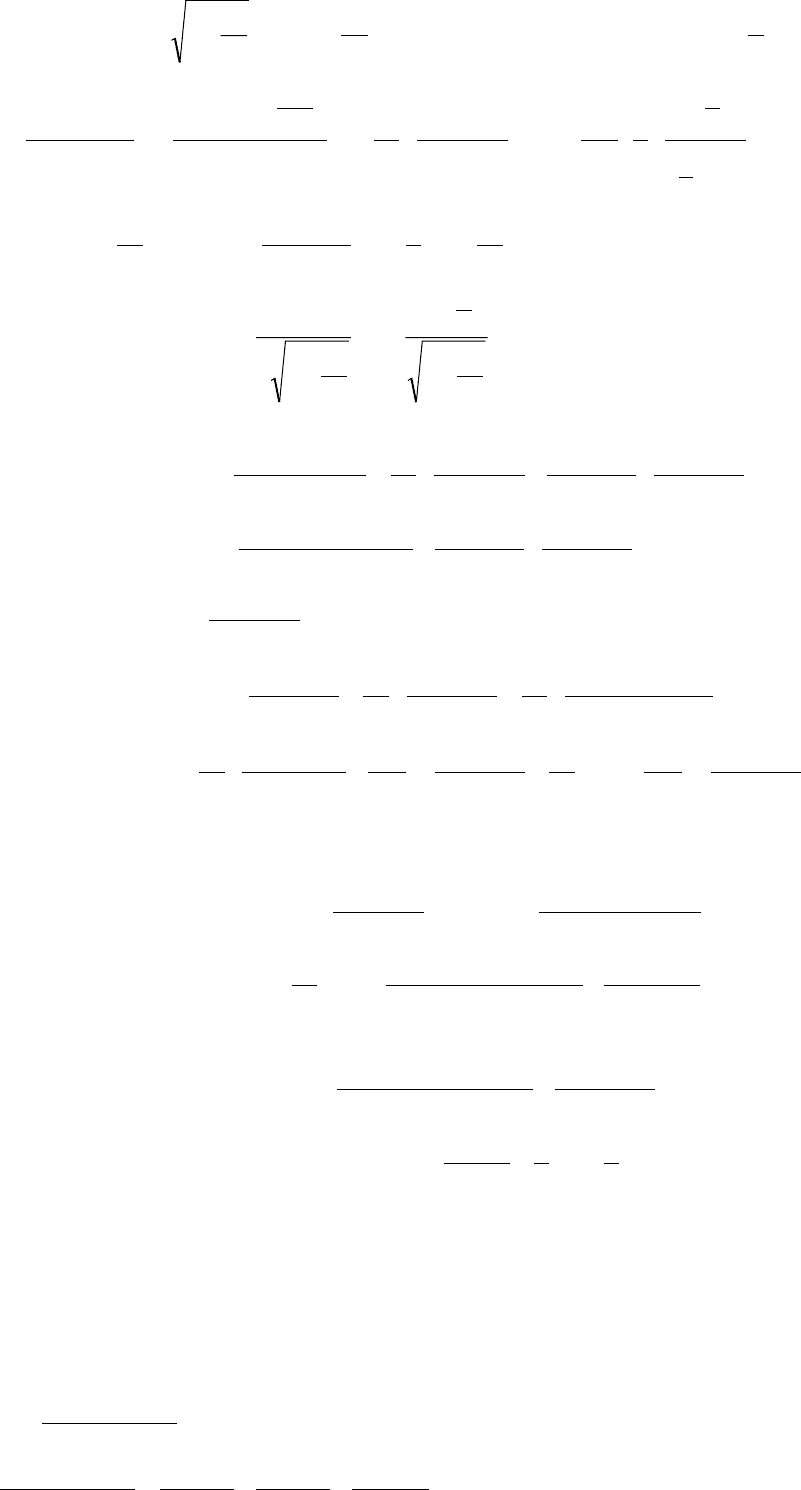
Положим .0
4
p
q
4
p
q
22
>−−+=
a Произведя подстановку
2
p
t =
, будем иметь
()
() ()
c
4
p
q
2
p
x
arctg
4
p
q2
MpN2
qpxxln
2
M
c
a
t
arctg
a2
MpN2
atln
2
M
1
a
t
a
t
d
a
1
2
Mp
N
at
atd
2
M
dt
at
2
Mp
NMt
qpxx
NMx
22
222
2
22
22
222
+
−
+
−
−
+
+++=+
−
++=
+
−+
+
+
=
+
−+
=
++
+
∫∫∫∫
IY. Аналогично III
получаем
()
(
)
() ()
()
() ()
∫
∫∫∫
+
−
+
+−
=
=
+
−
+
+
+
=
++
+
−
λλ
λλλ
λ
22
1
22
2222
22
2
at
dt
2
MpN2
at12
M
at
dt
2
MpN2
at
atd
2
M
qpxx
NMx
Обозначим
()
∫
+
=
λ
λ
22
at
dt
K
. Установим для этого интеграла рекуррентную формулу
() ()
(
)
[
]
()
() ()
()
()
∫∫∫
∫∫∫
+
+
−=
+
−
+
=
=
+
−+
=
+
=
+
=
−
−
λ
λ
λλ
λλλ
λ
22
22
2
1
2
22
2
1
22
2
22
222
2
22
2
2
22
at
atd
t
a2
1
K
a
1
at
tdt2
t
a2
1
at
dt
a
1
at
dttat
a
1
at
dta
a
1
at
dt
K
Для вычисления последнего интеграла применим формулу интегрирования по
частям, полагая в ней u=t, du=dt
()
()
()
()
1
2222
22
at1
1
,
at
atd
d
−
+−
−=
+
+
=
λλ
λ
υυ
()
()
()
1
2
1
222
1
2
K
1a2
1
at1a2
t
K
a
1
K
−
−
−
−
−
+−
+=
λ
λ
λλ
λ
λ
Отсюда
()
()
()
c
a
t
arctg
a
1
a
t
dt
K )1(
K
22a
32
at1a2
t
K
22
1
1
2
1
222
+=
+
==
−
−
+
+−
=
∫
−
−
λ
λ
λ
λ
λ
λ
λ
Используя рекуррентную формулу, вычислим К
2
, K
3
, ... и т.д.
Замечание. На практике К
λ
чаще вычисляют непосредственно с помощью
подстановки t=a
⋅tgu
Примеры.
1.
∫
−− )2x)(1x(
xdx
2
)2x(3
2
)1x(6
1
)1x(2
1
)2x)(1x(
x
2
−
+
+
−
−
−
=
−−
,
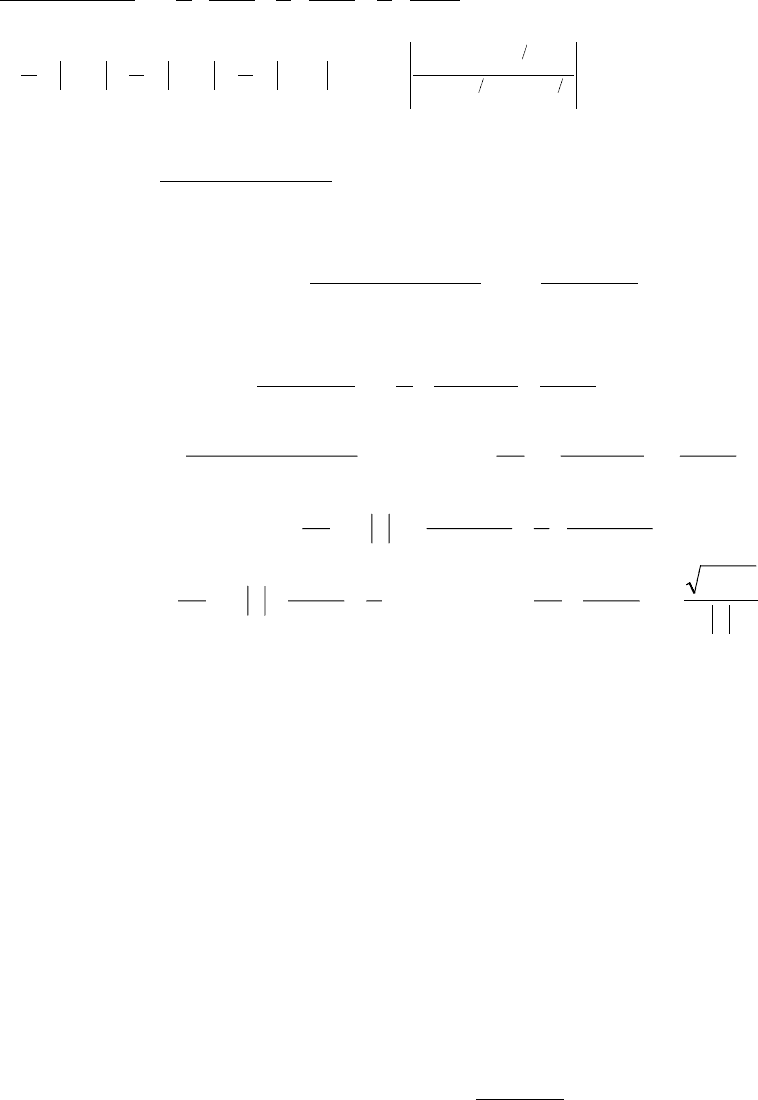
C
)1x()1x(
)2x(
lnC2xln
3
2
1xln
6
1
1xln
2
1
2x
dx
3
2
1x
dx
6
1
1x
dx
2
1
)2x)(1x(
xdx
6121
32
2
+
+−
−
=+−++−−−=
=
−
+
+
−
−
−=
−−
∫∫∫∫
2. Вычислим
∫
+
−++
dx
)1x(x
1x2x2x
22
246
. Согласно общему правилу, выделим целую
часть, разделив числитель на знаменатель; получим
22
2
22
246
)1x(x
1x
x
)1x(x
1x2x2x
+
−
+=
+
−++
.
Правильную рациональную дробь разложим на простейшие
1x
x
)1x(
x2
x
1
)1x(x
1x
22222
2
+
+
+
+−=
+
−
, отсюда
C
x
1x
ln
1x
1
2
x
C)1xln(
2
1
1x
1
xln
2
x
1x
)1x(d
2
1
1x
)1x(d
xln
2
x
dx
1x
x
)1x(
xdx2
x
dx
xdxdx
)1x(x
1x2x2x
2
2
2
2
2
2
2
2
2
22
22222
246
+
+
+
+
−=+++
+
−−=
=
+
+
+
+
+
+−=
=
+
+
+
+−=
+
−++
∫∫
∫∫∫∫∫
6.8.2. Интегрирование некоторых иррациональностей
6.8.2.1. Рациональные функции от нескольких аргументов
Определение 1. Многочленом степени n от двух аргументов x и y называется
выражение вида
n
n0
n
0n
2
0211
2
20011000n
ya...xa...yaxyaxayaxaa)y,x(P +++++++++=
,
в котором через
обозначены постоянные вещественные числа
такие, что среди чисел
есть хотя бы одно число, отличное от нуля.
n00n1000
a,...,a,...,a,a
1)1n(0n
,...,a,a
− n0
a
Определение 2. Рациональной функцией от двух аргументов x и y называется
выражение вида
)y,x(Q
)y,x(P
)y,x(R
m
n
=
,
где P
n
(x,y) и Q
m
(x,y) - многочлены от двух переменных степени n и m
соответственно.
Утверждение. Если R(x,y) - рациональная функция от двух аргументов x и y,
R
1
(t), R
2
(t), R
3
(t) - три произвольных рациональных функции от одной переменной
t, то выражение
(
)
)t(R)t(R ),t(RR
321
⋅
представляет собой рациональную функцию от одной переменной.
Замечание. В дальнейшем для доказательства интегрируемости в элементарных
функциях некоторых выражений мы будем посредством специально подобранной
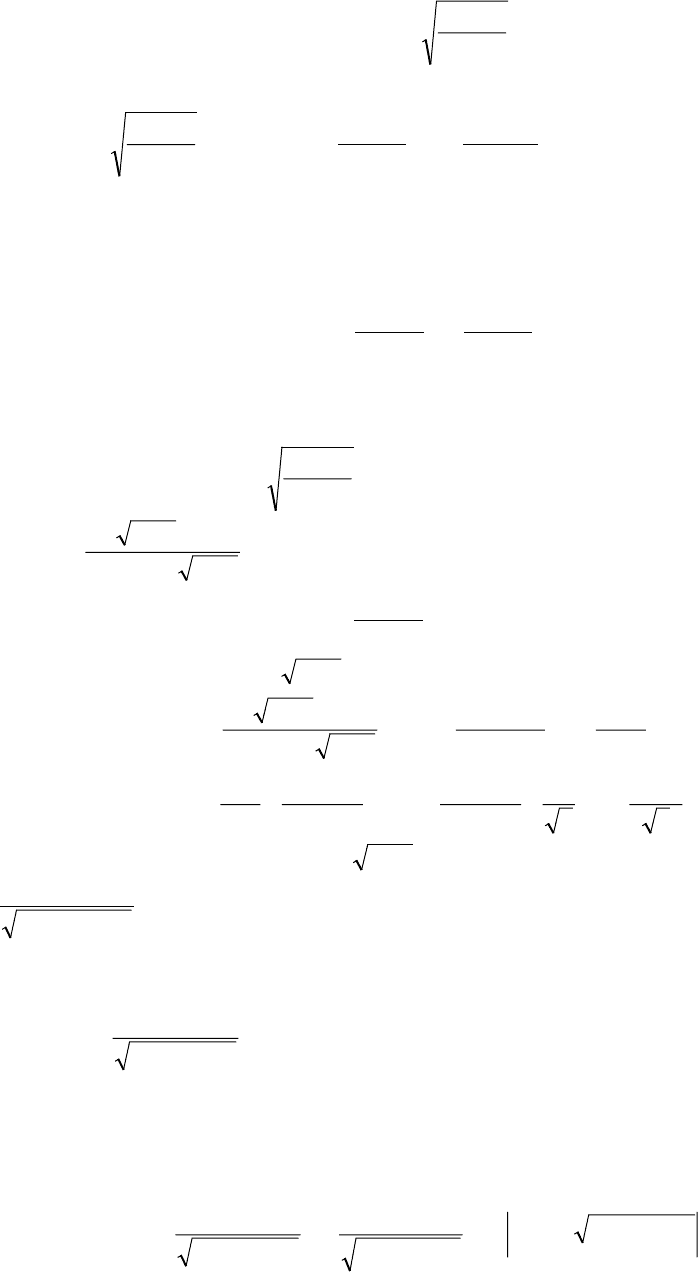
подстановки сводить интеграл от рассматриваемых выражений к интегралу от
рациональной дроби.
6.8.2.2. Интегрирование выражений вида
+
+
m
x
x
,xR
δγ
βα
,
где m
∈N
+
, α, β, γ, δ = const.
Положим
m
x
x
t
δγ
βα
+
+
=
, тогда
)t(
t
t
x ,
x
x
t
m
m
m
ϕ
γα
βδ
δγ
βα
≡
−
−
=
+
+
=
.
Интеграл перейдет в
.
()
∫
′
⋅ dt)t(t),(R
ϕϕ
Аналогично можно рассмотреть рациональные функции нескольких переменных
и интегралы вида
∫
+
+
+
+
dx,...
x
x
,
x
x
,xR
sr
δγ
βα
δγ
βα
,
где все показатели r, s, ... рациональны; надо лишь привести эти показатели к
общему знаменателю m, чтобы под знаком интеграла получить рациональную
функцию от x и радикала
m
x
x
δγ
βα
+
+
.
Пример.
∫
+−+
++
dx
1x)1x(
21x
2
.
Здесь дробно-линейная функция
δγ
β
α
+
+
x
x
, в частности, свелась просто к линейной
функции x+1. Полагаем
1tx ,1xt
2
−=+=
, тогда
C
3
1t2
arctg
3
2
1tt
)1t(
lndt
1tt
2t2
1t
2
dt
1t
2t
2
tt
tdt)2t(
2dx
1x)1x(
21x
2
2
2
34
2
+
+
−
++
−
=
++
+
−
−
=
=
−
+
=
−
+
=
+−+
++
∫
∫∫∫
где остается лишь подставить
1xt +=
.
а)
∫
++ cbxax
dx
2
Этот интеграл легко сводится к табличному, если
выделить в трехчлене ах
2
+bх+c полный квадрат.
Пример
∫
++ 5x2x
dx
2
x
2
+2x+5 = (x+1)
2
+4
Отсюда,
∫∫
+++++=
++
+
=
++
C5x2x1xln
5)1x(
)1x(d
5x2x
dx
2
22
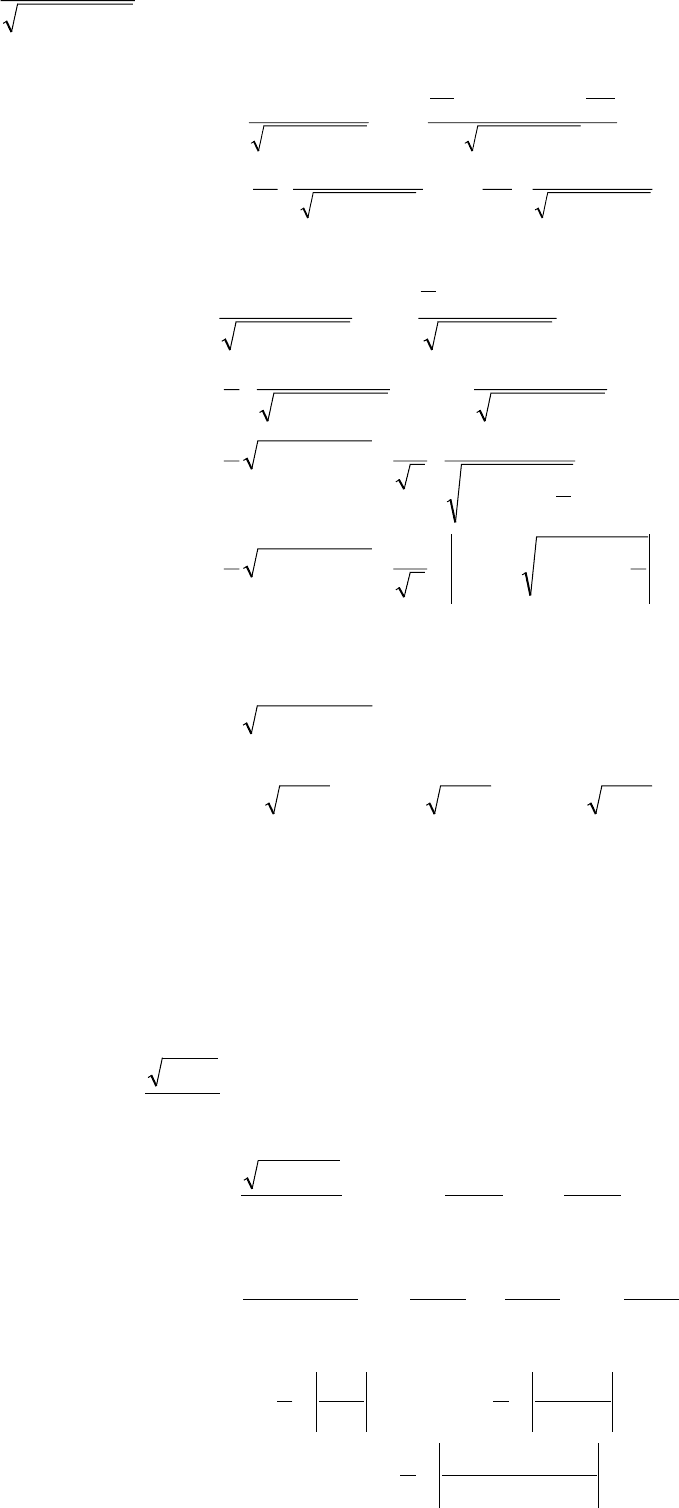
б)
∫
. В числителе дроби необходимо выделить производную
квадратного трехчлена.
++
+
dx
cbxax
BAx
2
∫∫
∫∫
++
−+
++
++
=
=
++
−++
=
++
+
cbxax
dx
)
a2
Ab
B(
cbxax
)cbxax(d
a2
A
dx
cbxax
a2
Ab
B)bax2(
a2
A
dx
cbxax
BAx
22
2
22
Пример
C
2
1
x4x2xln
2
13
1x8x2
2
5
2
1
x4x
dx
2
13
1x8x2
2
5
1x8x2
dx
13dx
1x8x2
8x4
4
5
dx
1x8x2
13)8x4(
4
5
dx
1x8x2
3x5
22
2
2
22
22
+++++−++=
=
++
−++=
=
++
−
++
+
=
=
++
−+
=
++
−
∫
∫∫
∫∫
6.8.2.3. Тригонометрические и гиперболические подстановки
В интегралах вида
(
)
∫
++ dxcbxax,xR
2
можно выделить полный квадрат в
трехчлене ах
2
+bx+c и свести их линейной заменой к интегралам вида
(
)
(
)
(
)
∫
∫
∫
−+− dt1t,tR ,dtt1,tR ,dtt1,tR
222
.
Для вычисления этих интегралов часто оказывается удобным использовать
тригонометрические подстановки
t=sinu, t=cosu, t=tgu,
а также гиперболические подстановки
t=shu, t=chu, t=thu.
Пример
∫
−
= dx
x
x1
J
2
.
Положим, x=sint, тогда dx=costdt и заданный интеграл принимает вид
=+
−
+
−=
=+
−
+
−=+
−
+
−=
=
=
−
−
−
−
=
−
−=
−
−=
>
===
−
=
∫∫∫∫
∫∫∫
C
)xcos(arcsin1
)xcos(arcsin1
ln
2
1
)xcos(arcsin
C
tcos1
tcos1
ln
2
1
tcosC
u1
u1
ln
2
1
u
tcosu
u1
du
du
u1
u1
u1
duu
tcos1
tcostdcos
)0t(cos
tdtsin
tsin
tcos
dt
tsin
tcos
tdtcos
tsin
tsin1
J
22
2
2
2
2
2
2
222

C
x
x11
lnx1
C
x11
x11
ln
2
1
x1
2
2
2
2
2
+
−+
−−=
=+
−−
−+
−−=
6.8.2.4. Интегрирование биноминальных дифференциалов
∫
+ dx)bxa(x
pnm
где а, b - любые постоянные; m, n и p - рациональные числа. Рационализирующая
подстановка существует в трех случаях.
1. p - целое
(
)
∫
dxx,xR
r
, где r - наименьшее общее кратное знаменателей рациональных
чисел m и n.
Подстановка
r
x=t
2.
n
1m +
- целое.
Положим z=x
n
, обозначив
q1
n
1m
≡−
+
, будем иметь
∫∫
+=+ dzz)bza(
n
1
dx)bxa(x
qppnm
(q - целое).
Это есть интеграл вида
(
)
∫
+ dzbza,zR
s
, где s - знаменатель числа р.
Рационализирующая подстановка имеет вид
s
bzat += , или для исходного
интеграла
sn
bxat +=
.
3.
ð
n
1m
+
+
- целое. Сначала положим z=x
n
.dzb
z
a
,zRdzzb
z
a
n
1
dzz)bza(
n
1
dx)bxa(x
s
qp
p
qppnm
∫∫
∫∫
+=
+=
=+=+
+
Здесь p+q=p+
1
n
1m
−
+
- целое, поэтому рационализирующая подстановка
s
b
z
a
t +=
,
или для исходного интеграла
sn
baxt +=
−
, где s - знаменатель числа р.
Примеры.
1.
∫∫
==−=
+=
+
−
3
1
p ,
4
1
n ,
2
1
m ,dxx1xdx
x
x1
3
1
4
1
2
1
3
4
Так как
2
4
1
1
2
1
n
1m
=
+−
=
+
, то имеем второй случай (знаменатель р равен 3).
Положим
3
4
,x1t +=
()
(
)
dt1tt12dx ,1tx
3
32
4
3
−=−= , тогда
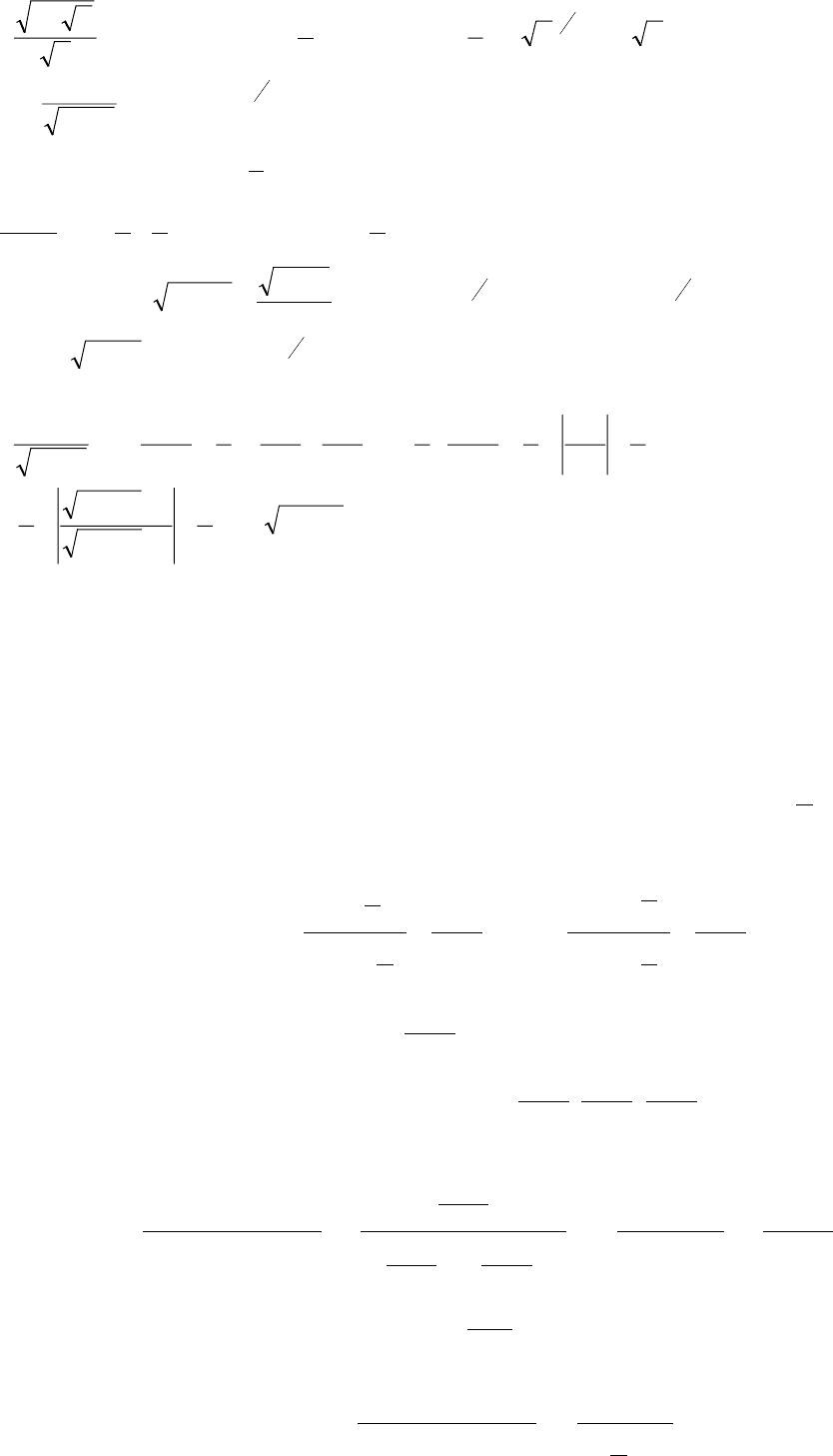
() ()
()()()
c7x14x1
7
3
c7t4t
7
3
dttt12dx
x
x1
4
3
4
4
3436
3
4
+−++=+−=−=
+
∫∫
2.
()
∫∫
−
+=
+
.dxx1x
x1
dx
4
1
40
44
Здесь m=0, n=4,
4
1
p −=
; третий случай интегрируемости, так как
−=−=+
+
0
4
1
4
1
p
n
nm
целое;
4
1
p −=
; знаменатель р равен 4.
Положим
() ()
dt1ttdx 1tx
x
x1
1xt
4
5
43
4
1
4
44
44
−−
−
−−=−=⇒
+
=+=
()
,1tttxx1
4
1
444
−
−==+
c1xarctg
2
1
11x
11x
ln
4
1
carctgt
2
1
1t
1t
ln
4
1
1t
dt
2
1
dt
1t
1
1t
1
4
1
1t
dtt
x1
dx
4
4
44
44
24
2
4
4
++−
−+
++
=
=+−
−
+
=
+
−
−
−
+
=
−
−=
+
−
−
−
∫∫∫∫
6.9. Интегрирование тригонометрических функций
6.9.1. Интегралы вида
(
)
∫
dxxcos,xsinR
, где R - рациональная функция
9.1. Такие интегралы приводятся к интегралам от рациональных функций с
помощью универсальной тригонометрической подстановки
.
2
x
tgt =
В результате
этой подстановки имеем
2
2
2
2
2
2
2
t
1
dt2
dx ;arctgt2x
t1
t1
2
x
tg1
2
x
tg1
xcos ;
t1
t2
2
x
tg1
2
x
tg2
xsin
+
==
+
−
=
+
−
=
+
=
+
=
()
∫∫
+
+
−
+
= .
t1
dt2
t1
t1
,
t1
t2
Rdxxcos,xsinR
22
2
2
Пример.
()
.c
2t
1
2t
dt
8t8t2
dt
2
5
t1
t1
3
t1
t2
4
t1
dt2
5xcos3xsin4
dx
2
2
2
2
2
2
+
+
−=
=
+
=
++
=
+
+
−
⋅+
+
⋅
+
=
++
∫∫∫ ∫
Возвращаясь к старой переменной, получим
∫
+
+
−=
++
.c
2
2
x
tg
1
5xcos3xsin4
dx
