Odekon M. Encyclopedia of paleoclimatology and ancient environments

Подождите немного. Документ загружается.

definition of the eigencoefficients of x( t) from ( 9), define those

of y(t) identically

ðf Þ¼

N1

n¼0

yðnÞv

ðkÞ

i2pnf

ð31Þ

and compute the cross-spectrum, S

( f )

ðf Þ¼

K1

k¼0

ðf Þy



ðf Þð32Þ

where, as before, the superscript “*” implies complex conju-

gate. It is usually more convenient to work with the complex

quantity, coherency,

gðf Þ¼

ðf Þ

½S

ðf ÞS

ðf Þ

ð33Þ

where S

( f ) is the spectrum of y(t). The absolute value jg( f )j

is known as coherence; however, because usage in the literature

has not been consistent, it is safer to use redundancy and refer

to g( f )as“complex coherency.” In practice, use of magnitude-

squared coherence, or MSC, defined as jg( f )j

is preferable.

In common with correlation coefficients, one has j g( f )j 1

with jg( f )j = 1 implying perfect correlation at frequency f,

and jg( f )j 0 implying that the series are not related at that

frequency. One can, and often does, encounter both conditions

in the same data, but usually, something in between occurs.

In data analysis one does not have the true coherence, but an

estimate. The formal distribution of coherence estimates is

complicated, but to answer the often-asked question “are these

two series coherent, or can they be treated as independent?,”

one can use a special case.

If the series are independent the probability distribution of

an estimate of MSC, say

C,is

C < ug¼1 ð1  uÞ

K1

ð34Þ

so, if one has K = 8 windows, the probability that an estimate of

coherence at a given frequency will be less than, say, 0.4 is 1 

(0.6)

= 0.972 As with most frequency-domain statistics, the pro-

blem is that there are as many independent frequency estimates

as there are data points with the result that, if one has 1,000 data

samples, the odds are good that, at some frequency, an estimate

will exceed the 99.9% significance level. This is where scientific

judgement comes in; if such an event occurs at, for example, a

period of 41,000 years in two long, well-dated ocean cores,

one would be remiss in saying there is no evidence for coher-

ence. If, however, it occurred at some “random” and otherwise

unknown frequency, the most likely explanation is that it is a

sampling fluctuation, not a new discovery. Here, looking at

the two power spectra, S

( f )andS

( f ) and the jackknife con-

fidence intervals of these and coherence can help. If there are

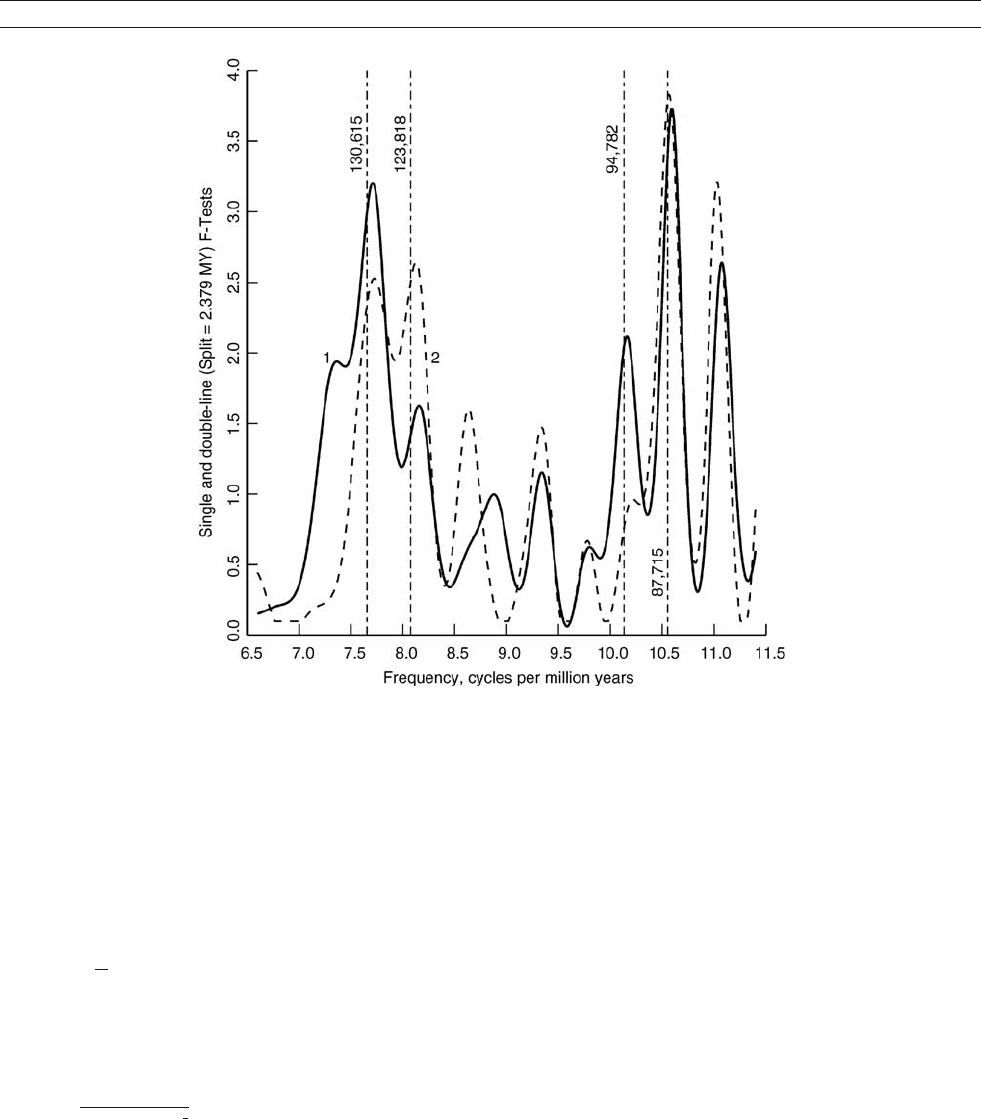
Figure T10 One (black) and two (dashed) line F-tests for periodic components in the eccentricity band. The two-line test assumed a frequency

separation corresponding to a period of 2.379 Myr (this is the separation between each of the two pairs of lines).

TIME–SERIES ANALYSIS OF PALEOCLIMATE DATA 955

pronounced peaks in both spectra, and the confidence intervals

are tight, the peak is much more likely to be real than it is if

the confidence bounds are wide and, particularly, if either or

both of the spectra have local minima at f.

It is also useful to count the number of frequencies where

the sample coherence is above the 10, 50, 80, and 90% signifi-

cance levels. If one finds, for example, that the fraction of esti-

mates above the nominal 90% level is 11% the series are

probably independent. If, in contrast, 30% of the coherence

estimates are above the nominal 90% point, one should assume

that the series are related.

Coherency is a complex quantity, but thus far, we have only

discussed its magnitude. Its phase is also important, primarily

because it shows the delay characteristics between the series.

One of the fundamental properties of the Fourier transform

(see e.g., Papoulis, 1962), is that a time-shifted function has

the Fourier transform

Ffxðt  t

Þ; t ! f g¼e

i2pft

FfxðtÞ; t ! f g

¼ e

i2pft

X ðf Þ

ð35Þ

so that the phase y( f )=2pft

+ phase{X( f )} has a linear

frequency trend. In a coherence estimate between x(t) and

x(t  t

), the conjugate on y

( f )in(32) cancels the phase

{X( f )} term leaving 2pft

. Thus, if x(t) and y(t) only differ in

relative amplitude and a time delay, the phase of the coherency

will be a linear slope in frequency. There are two things to

remember about doing this in practice: first, an phase estimate

is ambiguous to multiples of 2p radians or 360



, and these

phase ambiguities need to be resolved. One way is to take at

the difference between phases at adjacent frequencies and when

the magnitude of the difference exceeds 180



, add or subtract

360



with the sign chosen to minimize the difference. Second,

paleo-data is not noise-free, so that phase estimates are likely

to be unreliable unless the coherence is high. One strategy

for revealing phase trends is to pick frequencies where: (a)

the MSC has a local maxima, and (b) is significant above, say,

the 90% significance level. Then, at these frequencies, plot the

uncorrected phase y plus y  360



and y + 360



, and inspect.

Jackknife

The statistical jackknife was invented by Quenouille and named

by Tukey after the boy scout’s general purpose tool. It is a use-

ful and reliable method to estimate variances of complicated

statistics. The jackknife and the newer, and computationally

more difficult, bootstrap are covered in several recent texts

(see e.g., Efron and Tibshirani, 1998; Davison and Hinkley,

1999). Lahiri (2003) describes resampling methods for depen-

dent data, but the reliability of these for paleoclimate data has

yet to be determined. Generally speaking, resampling schemes

are intended for independent, identically-distributed data, and

so cannot be applied naively to time series data. The eigencoef-

ficients, {y

( f )} can be jackknifed (Thomson and Chave, 1991;

Thomson 2007), and this has been a reliable method of asses-

sing confidence limits on the various quantities. The basic rule

is to delete each eigencoefficient in turn, then compute the

mean and variance of the K “delete-one” estimates. To give a

specific example, if one uses the frequency where the F-test

is maximized as an estimate of location, one can write the

sequence of operations (24)to(25)as

all

¼ argmax

fFðf Þjx

ðf Þ; x

ðf Þ; ; x

K1

ðf Þg ð36Þ

Now repeat these calculations for 0  j  K  1 withholding

the j

eigencoefficient on each calculation

¼argmax

fFðf Þjx

; x

; ; x

j1

; x

jþ1

ðf Þ;

; x

K1

ðf Þg

ð37Þ

where the subscript nj means that the j

eigencoefficient has

been omitted. One now computes the average,



f ¼

K1

j¼0

ð38Þ

and the variance,

Varf



f g¼

K  1

K1

j¼0





ð39Þ

where the extra factor of K  1 in the variance formula occurs

because the different delete-one estimates contain dependent

data.

Nonstationarity and Holocene data

A major source of controversy in climate data is that the data is

nonstationary, while the majority of papers appear to implicitly

assume stationarity, at least when judged by the way they are

analyzed. Such a dichotomy is almost guaranteed to cause pro-

blems on all timescales, but the higher time resolution of much

Holocene data requires that the way the data is analyzed take

nonstationarity into account.

In specific, lunar and solar influences on climate appear to

be nonstationary. With the moon, the coupling is presumably

tidal modulation of storm tracks while several mechanisms

have been suggested for solar coupling. As specific examples,

attempts to detect the 18.61 year period of the lunar node, the

ordinary 11 year sunspot cycle, or the 22 year solar magnetic

cycle in instrumental climate data usually either fail or else

yield contradictory results. Both, however, appear to modulate

the statistics of the climate system and are easily detectable in

the central England temperature series as nonstationary fea-

tures. Another family of periods that commonly occurs in cli-

mate data is the 104-year “Suess” cycle and harmonically

related frequencies. While data from ocean and lake cores

rarely have fine enough sampling to resolve these frequencies,

the way they enter into instrumental data carries an important

lesson for the analysis of paleo data. To put this idea into more

definite form consider two oversimplified examples:

ðtÞ¼xðtÞþa cos 2pf

t; ð40Þ

and

ðtÞ¼ða þ b cos 2pf

tÞy

ðt  1ÞþxðtÞð41Þ

where x(t) is an ordinary stationary process and a, a, and b

constants. In the first example, y

(t), the sinusoid is easily

detectable if a is sufficiently large and a long enough sample

of the process is observed. This is what is usually assumed.

Over a few years, the annual temperature cycle is of approxi-

mately this form. However, over longer time spans, the more

complicated form of the annual cycle described in Thomson

(1995) must be considered. In the second example, y

(t) the

periodic component only enters because it modulates the struc-

ture of the process. Thus, even though y

(t) varies periodically,

956 TIME–SERIES ANALYSIS OF PALEOCLIMATE DATA

it is not an additive periodicity and something more compli-

cated than a simple spectrum is necessary to detect it.

As an example, Figures T11 and T12 show dynamic spectra

and F-tests for the benthic d

C record from Core V19-30

(Shackleton and Pisias, 1985). The data was gap-filled and

interpolated to be equally-spaced in time, then prewhitened

using an AR-1 prediction error filter

yðtÞ¼xðtÞaxðt  1Þ; t ¼ 1; ...N  1 ð42Þ

with a  0.99878, the one-step autocorrelation. Next, adap-

tively weighted multitaper spectra (17) and F–tests were

computed on 399 overlapping 8,000 year blocks each offset

by 800 years. Because the prewhitening reduces the range of

the spectrum, extreme bias protection was not as essential, so

a time-bandwidth product of c

= 2.7 and K = 4 tapers were

used on each block. However, even with prewhitening, one

notes that the range of the spectrogram, Figure T11,is> 10

The corresponding F –test (Figure T12) shows a band of rea-

sonably consistent maxima around 400 c/Myr (  2,500 years)

and another near the Bond period (Bond et al., 2001)of

1,500 years, or 666 c/Myr . Because short windows were

used in this example to highlight nonstationary aspects of the

data, the fact that these are observed at all is rather surprising.

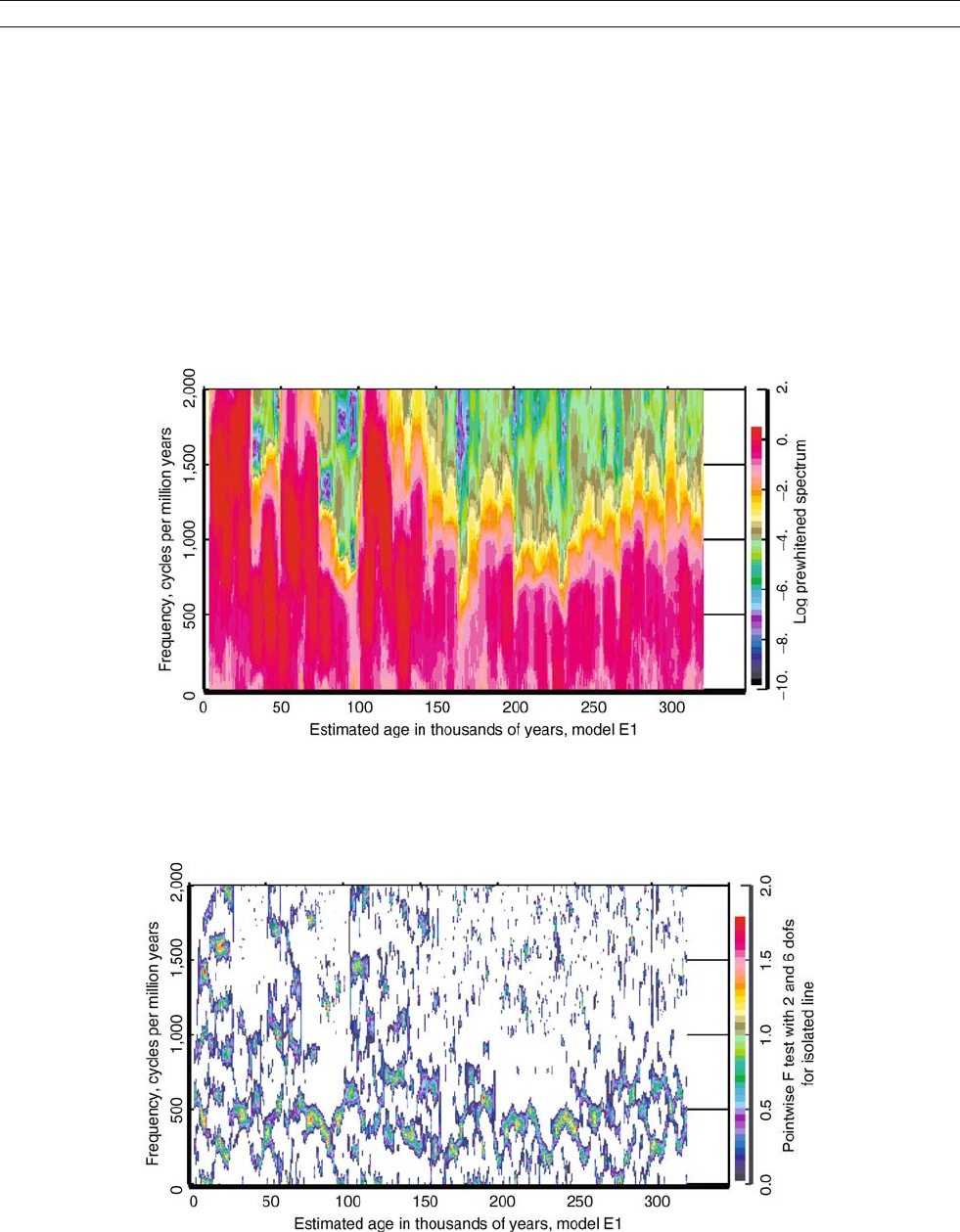
Turning again to the spectrogram (Figure T11), one of the

more prominent features is the series of vertical “stripes” where

Figure T11 Log

of a multitaper spectrogram for d

C in marine core V19-30. 8,000-year blocks, offset by 800-years were used with

= WT = 2.7 and K = 4 tapers on each block. The data was prewhitened using an autoregressive filter of order 1 (also known as a prediction

error filter) and, even so, the range of the spectrum exceeds ten orders of magnitude. Much of the apparent structure appears to be systematic.

Figure T12 The single-line F-test, (25), for d13C in Core V19-30 with parameters as in Figure T11. The most unusual feature of this plot is the

band of reasonably significant peaks visible near 440 c / Myr, corresponding to an average period of about 2,300 years.

TIME–SERIES ANALYSIS OF PALEOCLIMATE DATA 957

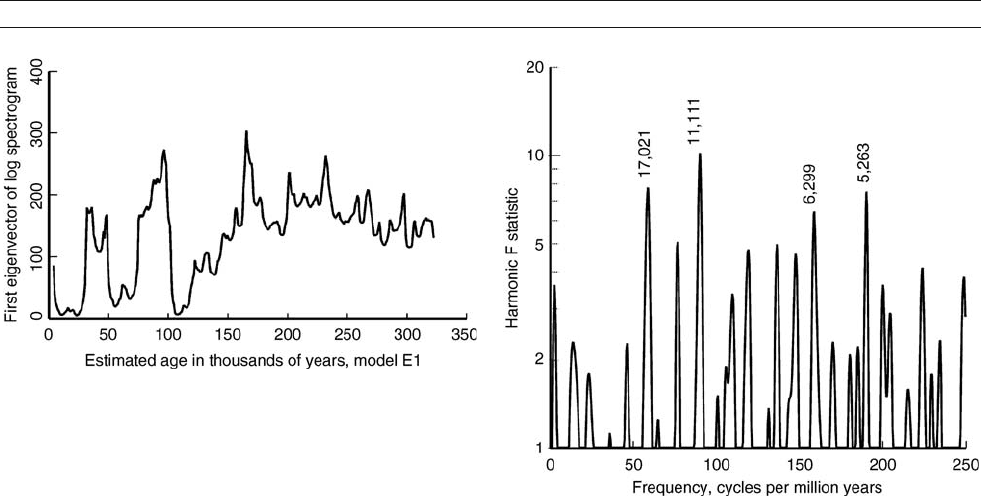
one can count  13 during the first 150,000 years. This corre-

sponds to an approximate period of  11,500 years, about one-

half the 23,000 year precession cycle. More formally, on taking

the singular value decomposition (SVD) of the log-spectrogram

as described in Thomson (1990b), one finds that the first eigen-

vector accounts for more than 95 % of the variation on the log

scale. This eigenvector is shown in Figure T13 where the most

alarming features are the abrupt transitions.

Wavelets, Lomb –Scargle, Blackman–Tukey

There are several estimates that should be avoided when ana-

lyzing paleoclimate data. Some, including the periodogram

and Blackman–Tukey estimates, are simply obsolete. It has

been recognized for over a century (Rayleigh, 1903), that the

periodogram is unreliable. Thomson (1977) has shown exam-

ples where the periodogram was in error by over a factor of

over most of the frequency range. Examples where it is

off by a factor of 10

and more, are common in geophysical

problems.

The Blackman–Tukey estimate is a smoothed periodogram

and inherits its bias problems, a fact that was recognized by

Tukey himself. In Tukey (1967), John was recommending

“direct” spectrum estimates with data tapering, basically the

k = 0 term in (14).

Lomb–Scargle estimates (Lomb, 1976; Scargle, 1981) are

simply least-squares fits to the data with a single sinusoid at a

time, and reduce to the ordinary periodogram when the data

is equally-spaced. They have their place, but are even more

dangerous than the ordinary periodogram. For most of the pro-

blems considered here, it is safer to interpolate the data to an

equally-spaced grid, then proceed as above. This is certainly

the case if only a few samples are missing.

Wavelets, again, are dangerous for unskilled users. More

than one example exists where a wavelet analysis was used to

“prove” that precession was frequency modulated. The problem

lies in (26); that is, when one makes the effective window

length T shorter, as one does in a wavelet analysis, the variance

of a frequency or period estimate increases as T

3

. Thus, if one

uses a short window, line frequencies appear to be variable.

This said, if wavelets are appropriate, read Daubechies

(1992), Mallat (2001), and Percival and Walden (2000).

Summary and Recommendations

The major facts to remember in the analysis of paleoclimate

data are as follows:

Analysis of paleoclimate data is difficult. Noting the efforts

that have gone into getting general circulation models to repro-

duce even fairly gross features of the climate system, one

should not expect that the analysis of data produced by the real

(and obviously far more complicated) climate system to be

simple.

The complexity of the data is not helped by the timing being

uncertain. However, a carefully tuned series is preferable to an

untuned one. While there is still some debate about whether the

tuning process is a form of circular argument, my opinion is

that the major remaining uncertainty is the change in preces-

sion and obliquity from glacial loading, and the earth’s

response to this loading.

The power spectrum is almost always more informative that

the autcovariance.

The best way to estimate a power spectrum from data is by

multitaper methods.

Blackman–Tukey estimates are obsolete and should not be

used. Parametric methods (ones based on autoregressive, mov-

ing average, and related models) rarely work well enough to

bother computing them. Similarly, the periodogram should

never be used as a spectrum estimate.

Paleoclimate data is almost certainly nonstationary, but

much of the nonstationarity appears to be systematic. One

should attempt to identify it.

As always, try several different methods to analyze data. It

is recommended to choose the method that gives a good

description of the observations with the simplest assumptions.

David J. Thomson

Figure 13 The first eigenvector in the time dimension of the SVD of lnS

(t,f) of the core V19-30 d

C data shown in Figure T11. This is the

eigenvector corresponding to the largest singular value.

Figure T14 The F-test for periodic components from a multitaper of

the eigenvector shown in Figure T13 using c

= 4 and K = 5. Periods of

components with individual significance levels above the 97 % level are

shown.

958 TIME–SERIES ANALYSIS OF PALEOCLIMATE DATA

Bibliography

Berger, A., 1977. Long-term variations of the earth’s orbital elements.

Celestial Mech., 15,53–74.

Berger, A., 1978. Long-term variations of daily insolation and quaternary

climatic changes. J. Atmos. Sci., 35, 2362–2367.

Bond, G., Kromer, B., Beer, J., Muscheler, R., Evans, M., Showers, W.,

Hoffmann, S., Lotti-Bond, R., Hajdas, I., and Bonani, G., 2001.

Persistent solar influence on North Atlantic climate during the

Holocene. Science, 294, 2130–2136.

Daubechies, I., (1992). Ten Lectures on Wavelets. Philadelphia: SIAM.

Davison, A.C., and Hinkley, D.V., 1999. Bootstrap Methods and their

Application. Cambridge: Cambridge University Press.

Efron, B., and Tibshirani, R.J., 1998. An Introduction to the Bootstrap.

Boca Raton, FL: Chapman & Hall/ CRC.

Gentleman, W.M., 1969. An error analysis of Goertzel’s (Watt’s) method

for computing Fourier coefficients. Comp. J., 12, 160–165.

Johnson, J., Thomson, D.J., Wu, E.X., and Williams, S.C.R., 1996.

Multiple-window spectrum estimation applied to in vivo NMR spectro-

scopy. J. Mag. Reson., B110, 138–149.

Kedem, B., 1994. Time Series Analysis by Higher Order Crossings. New

York: IEEE Press.

Lahiri, S.N., 2003. Resampling Methods for Dependent Data. New York:

Springer.

Laskar, J., 1990. The chaotic motion of the solar system: A numerical esti-

mate of the size of the chaotic zones. Icarus, 88, 266–291.

Laskar, J., 1999. The limits of earth orbital calculations for geological time-

scale use. Phil. Trans. R. Soc. Lond. A, 357, 1735–1759.

Laskar, J., Joutel, F., and Boudin, F., 1993. Orbital, precessional, and

insolation quantities for the earth from 20 myr to +10 myr. Astron.

Astrophys., 270, 522–533.

Lomb, N.R., 1976. Least-squares frequency analysis of unequally spaced

data. Astrophys. J. Suppl. Ser., 39, 447

–462.

Mallat, S., (2001). A Wavelet Tour of Signal Processing (2nd edn.). San

Diego: Academic Press.

Pälike, H., and Shackleton, N.J., 2000. Constraints on astronomical para-

meters from the geological record for the last 25 Myr. Earth Planet.

Sci. Lett., 182,1–14.

Papoulis, A., 1962. The Fourier Integral and its Applications. New York:

McGraw-Hill.

Percival, D.B., and Walden, A.T., 1993. Spectral Analysis for Physical

Applications; Multitaper and Conventional Univariate Techniques.

Cambridge: Cambridge University Press.

Percival, D.B., and Walden, A.T., 2000. Wavelet Methods for Time Series

Analysis. Cambridge: Cambridge University Press.

Rao, A.R., Hamed, K.H., and Chen, H.-L., 2003. Nonstationarities in

Hydrologic and Environmental Time Series. Dordrecht: Kluwer.

Rayleigh, L., 1903. On the spectrum of an irregular disturbance. Phil.

Mag., 41, 238–243. (In Scientific Papers by Lord Rayleigh, vol. V,

Art. 285, New York: Dover Publications, 1964, pp. 98–102).

Scargle, J.D., 1981. Studies in astronomical time series analysis. I. Model-

ing random processes in the time domain. Astrophys. J. Suppl. Ser., 45,

1–71.

Shackleton, N.J., and Pisias, N.G., 1985. Atmospheric carbon dioxide,

orbital forcing, and climate. In Sundquist E., and Broeker W. (eds.),

The Carbon Cycle and Atmospheric CO

: Natural Variations Archean

to Present. Washington: AGU, Geophysical Monograph 32,

pp. 412–417.

Shackleton, N.J., Berger, A., and Peltier, W.R., 1990. An alternative astro-

nomical calibration of the lower Pleistocene timescale based on ODP

site 677. Trans. R. Soc. Edinburgh Earth Sci., 81, 251–261.

Shackleton, N.J., Crowhurst, S., Hagelberg, T., Pisias, N.G., and Schneider,

D.A., 1995a. A new late Neogene time scale: Application to leg 138

sites. Proc. Ocean Drill. Program Sci. Results, 138,73–101.

Shackleton, N.J., Hall, M.A., and Pate, D., 1995b. Pliocene stable isotope

stratigraphy of site 846. Proc. Ocean Drill. Program Sci. Results,

138, 337–355.

Singleton, R.A., 1969. An algorithm for computing the mixed radix

fast Fourier transform. IEEE Trans. Audio Electroacoust., 17(2),

93–103.

Slepian, D., 1978. Prolate spheroidal wave functions, Fourier analy-

sis, and uncertainty V: The discrete case. Bell Syst. Tech. J.,

57, 1371–1429.

Thomson, D.J., 1977. Spectrum estimation techniques for characterization

and development of WT4 waveguide. Bell Syst. Tech. J., 56, Part I

1769–1815, Part II, 1983–2005.

Thomson, D.J., 1982. Spectrum estimation and harmonic analysis. Proc.

IEEE, 70, 1055–1096.

Thomson, D.J., 1990a. Quadratic-inverse spectrum estimates: Applications

to paleoclimatology. Phil. Trans. R. Soc. Lond. A, 332, 539–597.

Thomson, D.J., 1990b. Time series analysis of Holocene climate data. Phil.

Trans. R. Soc. Lond. A, 330, 601–616.

Thomson, D.J., 1995. The seasons, global temperature, and precession.

Science, 268,59–68.

Thomson, D.J. 2001. Multitaper analysis of nonstationary and nonlinear

time series data. In Fitzgerald, W., Smith, R., Walden, A., and

Young, P. (eds.), Nonlinear and Nonstationary Signal Processing.

Cambridge: Cambridge University Press, pp. 317–394.

Thomson, D.J., and Chave, A.D., 1991. Jackknifed error estimates for

spectra, coherences, and transfer functions. In Haykin, S. (ed.),

Advances in Spectrum Analysis and Array Processing

, vol. 1, chapter 2.

Englewood Cliffs, NJ: Prentice-Hall, pp. 58–113.

Thomson, D.J., Lanzerotti, L.J., and Maclennan, C.G., 2001. The inter-

planetary magnetic field: Statistical properties and discrete modes.

J. Geophys. Res., 106, 15941–15962.

Thomson, D.J., 2007. Jackknifing multitaper spectrum estimates. IEEE

Signal Processing Magazine, 24(7), 20–30.

Thomson, D.J., Lanzerotti, L.J., Vernon, F.L., III, Lessard, M.R., and

Smith, L.T.P., 2007. Solar modal structure of the engineering environ-

ment. Pr oceedings of the IEEE, 95, 1085–1132.

Tukey, J.W., 1967. An introduction to the calculations of numerical spec-

trum analysis. In Harris, B. (ed.), Spectral Analysis of Time Series,

New York: Wiley, pp. 25–46.

Weedon, G., 2003. Time–Series Analysis and Cyclostratigraphy.

Cambridge: Cambridge University Press.

Cross-references

Astronomical theory of climate change

Eccentricity

Obliquity

Ocean Drilling Program (ODP)

Precession, climatic

SPECMAP

TRANSFER FUNCTIONS

Introduction

Paleoecologists use a number of different methods to recon-

struct past changes in the Earth’s climate and environment.

One of the most useful is the analysis of the remains of micro-

scopic plants and animals preserved in ocean, lake, and mire

sediments. Interpretation of these biostratigraphic records is

usually based on the principle of uniformitarianism: that is,

knowledge of an organism’s present-day ecology and climate

preferences can be used to make inferences about past condi-

tions. Transfer functions are mathematical response functions

that allow paleoecologists to formalize this procedure by defin-

ing a series of equations that relate a set of biological species

data to climate or other environmental parameters.

The transfer function methodology has developed rapidly

since the early 1970s following the pioneering work of Imbrie

and Kipp (1971) on sea surface temperature reconstruction

from fossil foraminifera. Since then the approach has become

one of the main tools for studying environmental change on a

range of timescales, and has been used to derive quantitative

paleoclimate and other environmental estimates from various

TRANSFER FUNCTIONS 959

biological proxies preserved in different sedimentary archives

(Table T2).

Methods

The basic idea behind the transfer function approach to envir-

onmental reconstruction is that we can model a set of biological

responses (Y) as a function of one or more environmental para-

meters (X) (Birks, 1995):

Y ¼ fxðÞþerror

If we understood and could quantify the various physical, che-

mical and biological processes that determine the distribution

and abundance of the taxa in question, we could derive the

response functions f(x) directly. Such detailed autoecological

information is usually lacking, so instead we adopt an empirical

approach and relate the modern distribution and abundance of

taxa to contemporary environmental measurements. This

usually involves a modern “training” or “calibration” dataset

consisting of biological census counts extracted from surface

sediments together with environmental measurements from

the same sites. The relationship between the modern biological

and environmental datasets is then used to solve f(x) and the

resulting transfer functions are applied to fossil assemblages

in order to derive estimates of the environmental variable for

times in the past (Figure T15).

The resulting accuracy and applicability of the transfer func-

tion depends in part on the size and quality of the training set

from which it is derived. The training set is usually derived

from the same type of sedimentary environment as the fossil

material to minimize the influence of taphonomic effects. More

important is that the training set includes the range of taxa pre-

sent in the fossil assemblages and that it spans the range of

environments likely to have occurred in the past. This require-

ment cannot always be met using small regional trainings sets

so paleoecologists are increasingly collaborating to merge

regional datasets into large continental or global training sets

for some organisms (e.g., pollen: Davis et al., 2003; foramini-

fera: Kucera et al., 2005).

Modern training sets usually contain many taxa (20–300),

have abundances expressed as percentages or proportions

(i.e., have a constant-sum constraint), and individual taxa often

exhibit a non-linear relationship with the environmental vari-

able of interest. Such properties make the derivation of f(x)a

difficult statistical problem of multivariate calibration. Not sur-

prisingly, a number of different numerical methods have been

proposed, and some have a stronger ecological or statistical

basis than others (see Birks, 1995; ter Braak, 1995).

Most methods can be classified into one of two groups.

The first seeks to fit a single model to the training set data,

providing a generalized description of the relationship between

taxa and environment. Examples of this approach are the

principal component regression method of Imbrie and Kipp

(1971), neural networks (Malmgren et al., 2001)usedinpaleo-

ceanography, and the weighted averaging method and its

extension – weighted averaging partial least squares – used

in paleolimnology (e.g., Birks, 2003 ). The second group of

methods includes the so-called modern analog technique

(MAT) and its variants, known in the statistical literature as

k-nearest neighbors. This is perhaps the most simple and intui-

tive method of calibration: rather than fitting a single model to

the entire training set, MAT derives what is essentially a local

model by searching the modern data for samples that most clo-

sely resemble the fossil assemblage. The dissimilarity between

the modern and fossil assemblages is calculated by a numerical

distance measure (e.g., squared chord distance), and a recon-

struction is derived by averaging the environmental value of a

small number (usually 10) of the closest analogs.

Differences in the properties of proxies in terms of training

set size, taxonomic diversity, and complexity of the species-

environment relationship make some numerical techniques

more useful than others for particular biological groups. How-

ever, it is clear that there is no single mathematical technique

that can be recommended as optimal, on either theoretical or

empirical grounds. Because of this, many paleoecologists have

moved away from the search for a single “best” method and

recommend comparing results from several different techniques

and combining them to derive a consensus reconstruction (e.g.,

Birks, 2003; Kucera et al., 2005).

How accurate are the reconstructions?

Given a modern training set and a series of fossil assemblages,

all transfer function methods will produce some result. It is

therefore important to evaluate the accuracy and reliability of

the reconstructions. Direct comparison of the reconstructions

with historical monitoring records provides perhaps the most

powerful way of validating records for the recent past (e.g., Mal-

mgren et al., 2001; Larocque and Hall, 2003). Over longer per-

iods, independent environmental measurements are usually not

available and some form of internal validation based on an ana-

lysis of the training set must be used. In this case, the prediction

error of the transfer function is typically estimated by comparing

the measured environmental variable with the predicted value

across the training set samples. Since the same data is being used

to both generate and test the model, some form of data splitting

or computer-intensive resampling scheme is employed to better

simulate the likely errors when the transfer function is applied to

new data outside the training set (Birks, 1995).

One of the main assumptions of the transfer function

approach is that the modern training set encompasses the range

Table T2 The main biological proxies used in transfer functions and applications

Biological proxy Archive Application Examples

Foraminifera, diatoms, coccoliths,

dinoflagellates

Marine sediments Sea surface temperature Kucera et al. (2005); Andersen et al. (2004);

Peyron and De Vernal (2001)

Terrestrial pollen Marine, lake and mire

sediments

Temperature, precipitation,

growing degree days

Davis et al. (2003)

Coleoptera Lake and mire

sediments

Temperature Coope (2002)

Diatoms, chironomids, Cladocera Lake sediments Temperature, salinity, pH,

nutrients

Mackay et al. (2003); Larocque and Hall (2003)

960 TRANSFER FUNCTIONS

of biological and environmental variability expressed by the

fossil assemblages. This can be partially tested by calculating

an analog measure between individual fossil samples and the

training set: reconstructions for samples that lack good modern

analogs are likely to be less reliable and should be treated with

caution. Comparison of reconstructions obtained from the

same fossil assemblages using different numerical procedures

can highlight technique-specific bias, and together with analog

measures, can be used to give a reliability rating to each re-

constructed value (Kucera et al., 2005). In some cases, paleoe-

cologists are able to compare reconstructions derived from

independent biological or geochemical proxies measured on

the same, or closely related, sedimentary sequences (e.g., Birks

et al., 2000; Bard, 2001; Larocque and Bigler, 2004). Such com-

parisons are beginning to focus attention on the potential biases

of individual proxies and on the need to understand the pro-

cesses controlling organism distribution in the training set better.

An important corollary of the above assumption is that not

only should the relationship between biota and the environmen-

tal variable of interest be invariant through time, but also that

the joint distribution of other environmental factors controlling

species distribution should have been the same in the past as it

is today. This assumption is probably violated in many cases.

Where the environmental variable is a strong determinant of

species distribution and biological changes are large (e.g., in

studies of recent lake acidification or eutrophication), such

biases are likely to be small. Over longer timescales where

the current training set does not encompass the past range of

environmental conditions, or where the environmental variable

being reconstructed is not a major determinant of species distri-

bution, biases may be significant and are a focus of current

research (e.g., Watkins and Mix, 1998; Anderson 2000).

Stephen Juggins

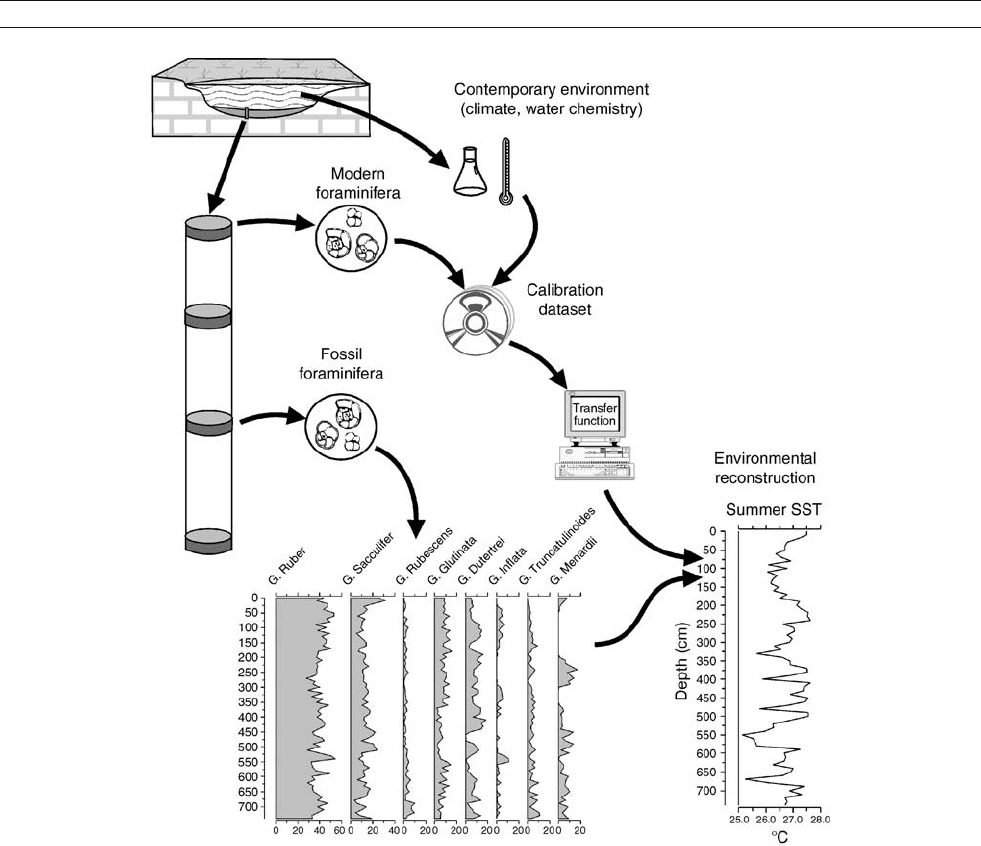
Figure T15 A schematic illustrating the transfer function approach to deriving a quantitative reconstruction of past sea-surface temperature from

foraminifer biostratigraphic data using a modern training or calibration dataset.

TRANSFER FUNCTIONS 961

Bibliography

Andersen, C., Koc, N., and Moros, M., 2004. A highly unstable Holocene

climate in the subpolar North Atlantic: Evidence from diatoms. Qua-

ternary Sci. Rev., 23, 2155–2166.

Anderson, N.J., 2000. Diatoms, temperature and climate change. Eur. J.

Phycol., 35, 307–314.

Bard, E., 2001. Comparison of alkenone estimates with other paleotem-

perature proxies. Geochem. Geophys. Geosyst., 2, doi:10.1029 /

2000GC000050.

Birks, H.H., Battarbee, R.W., and Birks, H.J.B., 2000. The development

of the aquatic ecosystem at Kråkenes Lake, western Norway, during

the late-glacial and early-Holocene - a synthesis. J. Paleolimnol., 23,

91–114.

Birks, H.J.B., 1995. Quantitative palaeoenvironmental reconstructions. In

Maddy, D., and Brew, J. (eds.), Statistical Modelling of Quaternary

Science Data, Technical Guide 5. Cambridge, UK: Quaternary

Research Association, pp. 161–254.

Birks, H.J.B., 2003. Quantitative palaeoenvironmental reconstructions from

Holocene biological data. In Mackay, A., Battarbee, R.W., Birks, H.J.B.,

and Oldfield, F. (eds.), Global Change in the Holocene. London: Arnold,

pp. 107–123.

Coope, G.R., 2002. Changes in the thermal climate in northwestern Europe

during marine oxygen isotope stage 3, estimated from fossil insect

assemblages. Quaternary Sci. Rev., 57, 401–408.

Davis, B.A.S., Brewer, S., Stevenson, A.C., and Guiot, J., 2003. The tem-

perature of Europe during the Holocene reconstructed from pollen data.

Quaternary Sci. Rev., 22, 1701–1716.

Imbrie, J., and Kipp, N.G., 1971. A new micropaleontological method

for quantitative paleoclimatology: Application to a Late Pleistocene

Caribbean core. In Turekian, K.K. (ed.), The Late Cenozoic Glacial

Ages. New Haven: Yale University Press, pp. 77–181.

Kucera, M., Weinelt, M., Kiefer, T., Pflaumann, U., Hayes, A., Weinelt, M.,

Chen, M.-T., Mix, A.C., Barrows, T.T., Cortijo, E., Duprat, J., Juggins, S.,

and Waelbroeck, C., 2005. Reconstruction of sea-surface temperatures

from assemblages of planktonic foraminifera: Multi-technique approach

based on geographically constrained calibration data sets and its applica-

tion to glacial Atlantic and Pacific Oceans. Quaternary Sci. Rev., 24,

951–998.

Larocque, I., and Bigler, C., 2004. Similarities and discrepancies between

chironomid- and diatom-inferred temperature reconstructions through

the Holocene at Lake 850, northern Sweden. Quaternary Int., 122,

109–121.

Larocque, I., and Hall, R.I., 2003. Chironomids as quantitative indicators of

mean July air temperature: Validation by comparison with century-long

meteorological records from northern Sweden. J. Paleolimnol., 29

475–493.

Mackay, A.W., Jones, V.J., and Battarbee, R.W., 2003. Approaches

to Holocene climate reconstruction using diatoms. In Mackay, A.,

Battarbee, R.W., Birks, H.J.B., and Oldfield, F. (eds.), Global Change

in the Holocene. London: Arnold, pp. 294–309.

Malmgren, B.A., Kucera, M., Nyberg, J., and Waelbroeck, C., 2001. Com-

parison of statistical and neural network techniques for estimating past

sea-surface temperatures from planktonic foraminifer census data.

Paleoceanography, 16, 520–530.

Peyron, O., and De Vernal, A., 2001. Application of artificial neural net-

works (ANN) to high-latitude dinocyst assemblages for the reconstruc-

tion of past sea-surface conditions in Arctic and sub-Arctic seas.

J. Quaternary Sci., 16, 699–709.

ter Braak, C.J.F., 1995. Non-linear methods for multivariate statistical cali-

bration and their use in palaeoecology: A comparison of inverse

(k-nearest neighbors, partial least squares and weighted averaging

partial least squares) and classical approaches. Chemometrics and Intel-

ligent Lab. Syst., 28, 165–180.

Watkins, J.M., and Mix, A.C., 1998. Testing the effects of tropical tempera-

ture, productivity, and mixed-layer depth on foraminiferal transfer func-

tions. Paleoceanography, 13,96–105.

Cross-references

Dendroclimatology

Nearest-Living-Relative Method

Ocean Paleotemperatures

Paleobotany

TRIASSIC-JURASSIC CLIMATES

Ever since the late nineteenth century discovery of fossil conifers,

ferns and cycadlike plants in Spitzber gen and Greenland, the

T riassic and Jurassic periods of geological time (250–144 Ma)

have been regarded as times of unusual global warmth. The

twentieth century discovery of continental drift and plate tec-

tonics did not explain paleoclimatic anomalies of forests at high

latitudes, and even higher paleolatitude fossil forests were

found in Antarctica. These observations, coupled with a likely

role for carbon dioxide in global warming comparable with

panes of a greenhouse, which was first suggested by nineteenth

century physicists John Tyndall and Svanté Arrhenius, have led

to the concept that “greenhouse paleoclimates” (as in Triassic

and Jurassic) alternated with “icehouse paleoclimates” (such

as Permian and modern) over the course of Earth history. In

the current atmosphere of early twenty-first century global

warming, the details and causes of such warm periods of the

geological past remain of great interest.

Rock and fossil record

Especially obvious as evidence of greenhouse global warmth in

the past are permineralized tree stumps and logs at high lati-

tudes, well south or north of the modern treeline. Early Triassic

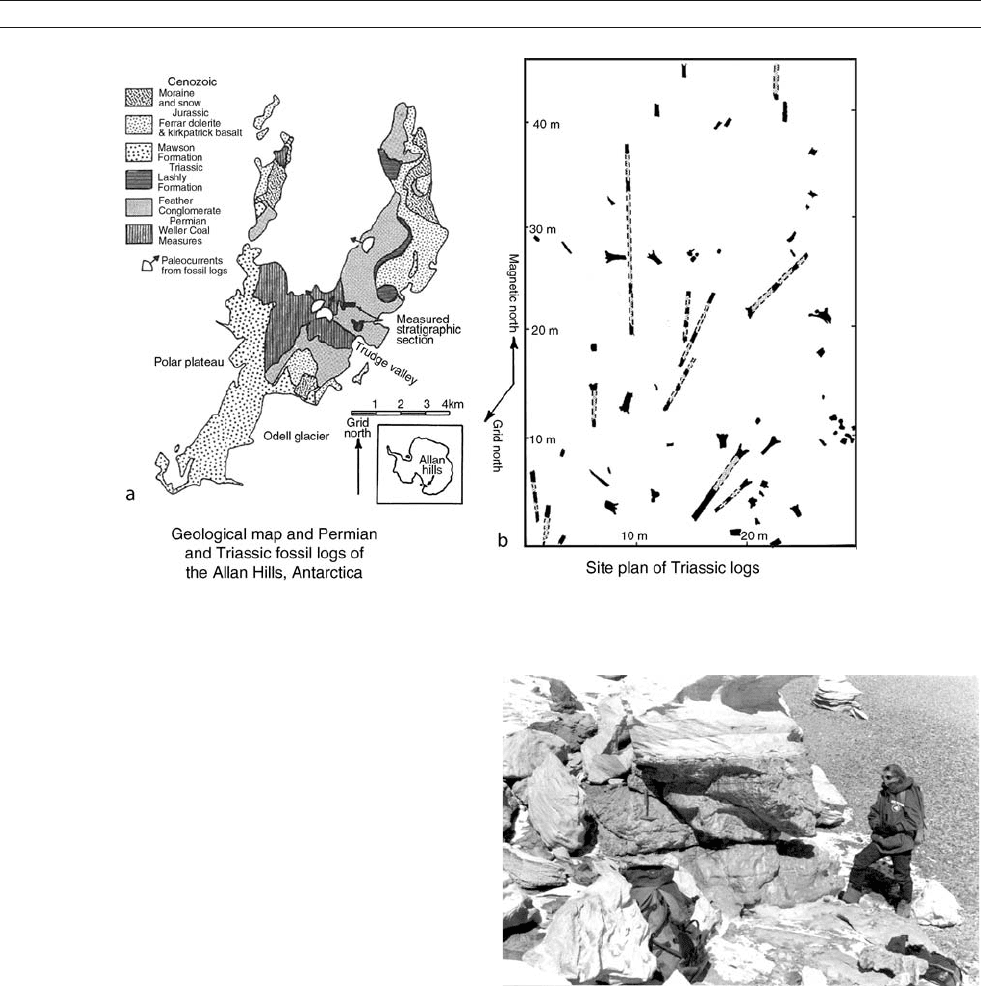
fossil logs from Antarctica (Figure T16), for example, grew at

paleomagnetically estimated paleolatitudes of 69–73



S, not

very different from present paleolatitudes (76



S); however, at

present there is a landscape of bare rock and ice with nothing

larger than endolithic lichens growing. The fossil logs are up

to 19 m long, and judging from their diameters compared with

those of living pines, would have been trees 50 m high (Retal-

lack, 1997a). Although these fossil logs are within ancient

stream deposits and have been transported, they are associated

with permineralized chunks of peaty soils that have not tra-

veled far. Furthermore, untransported ancient soils containing

large tree roots are found within the same sedimentary

sequence (Figure T17).

The marked tree rings of Antarctic permineralized logs

indicate strong climatic seasonality (Del Fueyo et al., 1995),

presumably due to an annual snowy season. Fossil leaves

of many high paleolatitude floras, such as the Dicroidium flora

of Antarctica (Figure T18), show evidence of deciduous leaf

shedding found in seasonally snowy climates today. The

petioles of the fossil leaves have basal smooth callus tissue

indicating that they were deliberately shed, rather than torn

from their branches. Other fossils from the Dicroidium

flora, presumably torn off during storms, show clustering of

leaves in bundles (Anderson and Anderson, 1985), similar to

short shoots and buds of cool temperate plants, such as oaks

and pines.

Living relatives of high latitude fossil plants were the great-

est surprise to pioneering paleobotanists. Jurassic floras of

Greenland are dominated by leaves like those of living cycads

and marattiaceous, matoniaceous, dipteridaceous and gleiche-

niaceous ferns, which are plants now found in warm temperate

and tropical climates. Subsequently it was shown that the ferns

belong to extinct species, and only a few of the cycadlike

leaves were closely allied to modern cycads. Many of the

cycadlike leaves belong to an extinct cycadlike group, the

cycadeoids, with very different reproductive structures. Never-

theless, many of the fern and cycadlike leaves were large, too

962 TRIASSIC-JURASSIC CLIMATES

large for polar tundra or taiga vegetation. Furthermore, some of

the fossils had a palmlike growth form, with a large terminal

meristem and a single parasol-like canopy of large spreading

leaves. Frost sensitivity of such large terminal meristems is

the main reason why palms, cycads and tree ferns fail to grow

much further north or south of 30



latitude, unless in a green-

house. This argument does not apply to fossil gleicheniaceous

ferns, which today are mainly scrambling vines, or to all fossil

cycadeoids and cycads, some of which differ from modern

cycads in having slender and copiously branching twigs (Willis

and McElwain, 2002). Nevertheless, the overall appearance of

some high latitude Jurassic floras is more like a Malaysian jun-

gle than taiga or tundra vegetation.

Fossil animals and their traces can also be evidence of

global warmth. Large labyrinthodont amphibians from the

early Triassic of Antarctica, for example, were probably

“cold blooded” (ectothermic poikilotherms) like modern alli-

gators of frost-free climates (Retallack and Krull, 1999).

The paleoclimatic significance of dinosaurs is less clear,

because their physiology (perhaps inertial or endothermic

homeotherms) does not have modern analogues. Ground-

dwelling termites are restricted to tropical and subtropical

regions (Retallack, 2001a), and could be exploited as paleocli-

matic indicators now that their distinctive nests have been

recognized in paleosols (Hasiotis and Dubiel, 1995). Coral

reefs spread to higher latitudes during global warming (Kies-

sling et al., 1999). However, some times of restricted reef dis-

tribution during the early (Pliensbachian) and middle Jurassic

(Bajocian) and earliest Cretaceous (Berriasian), as well as pro-

longed disappearance of reefs during the earliest Triassic

(Griesbachian), appear to have been due to mass extinctions,

rather than paleoclimatic cooling (Hallam and Wignall, 1997).

Fossil soils (paleosols) also present striking paleoclimatic

anomalies indicative of unusually warm polar paleoclimates.

Paleosols associated with early Triassic fossil logs in Antarctica

(Figure T17) not only confirm that trees grew nearby, but show

a degree of chemical leaching of common plant nutrients (Ca,

Mg, K, Na) comparable to that found no further south than



latitude. These paleosols are enriched in clay and chemi-

cally weathered to the same extent as modern Ultisols, which

Figure T16 Geological map, paleocurrents (a) and site plan of fossil stumps and logs in Early Triassic sandstones (b) of the Feather Conglomerate

in the Allan Hills, Victoria Land, Antarctica, currently at 76



S, and with estimated paleolatitude of 69–73



S (after Retallack, 1997a).

Figure T17 An ancient soil of early Triassic age from the Feather

Conglomerate in the Allan Hills, Antarctica. The clayey profile with large

root traces and cracks was buried by a cross-bedded sandstone of an

ancient river. Chemical analysis of this paleosol show that it was deeply

weathered and depleted in common plant nutrients (Ca, Mg, K, Na), like

modern Ultisols found no further south than 48



latitude (Retallack and

Krull, 1999).

TRIASSIC-JURASSIC CLIMATES 963

are a soil order found no further south than Tasmania and the

North Island of New Zealand and no further north than the

Chehalis lowlands of Washington State, USA (Retallack and

Krull, 1999). These non-calcareous Antarctic paleosols are evi-

dence of warm, as well as humid, paleoclimates.

Paleosols are especially useful paleoclimatic indicators

because they are found in many places where fossil plants are

not, as well as where conditions were suitably swampy, fre-

quently flooded, or covered by volcanics, leading to fossil plant

preservation (Retallack, 2001a). Paleosols thus provide a more

comprehensive view of Triassic and Jurassic global paleocli-

mate and ecosystems than fossil plants. Fossil rain forest plants

are not common, but rain forest paleosols (Oxisols) and their

characteristic horizons (bauxites and laterites) can be locally

common. Semiarid to subhumid shrubland and wooded shrub-

land, which can be inferred from fossil therapsids and dino-

saurs, also have a very limited paleobotanical record, but can

be inferred from sodic Aridisols and evaporites of winter-

wet subtropical regions and calcic Aridisols and calcretes of

summer-wet tropical to temperate regions (Retallack, 1997b).

Fossil plants of summer-wet subtropical forests (such as the

late Triassic flora of the Chinle Formation of Arizona) are asso-

ciated with ferric and calcic Alfisol paleosols. Fossil plants of

temperate broadleaf forests (such as the early Triassic flora of

the Newport Formation of Australia) are associated with Ultisol

paleosols. Fossil plants of cool temperate deciduous wood-

lands (such as the late Triassic flora of the Falla Formation of

Antarctica) are associated with humic Alfisols. Provisional

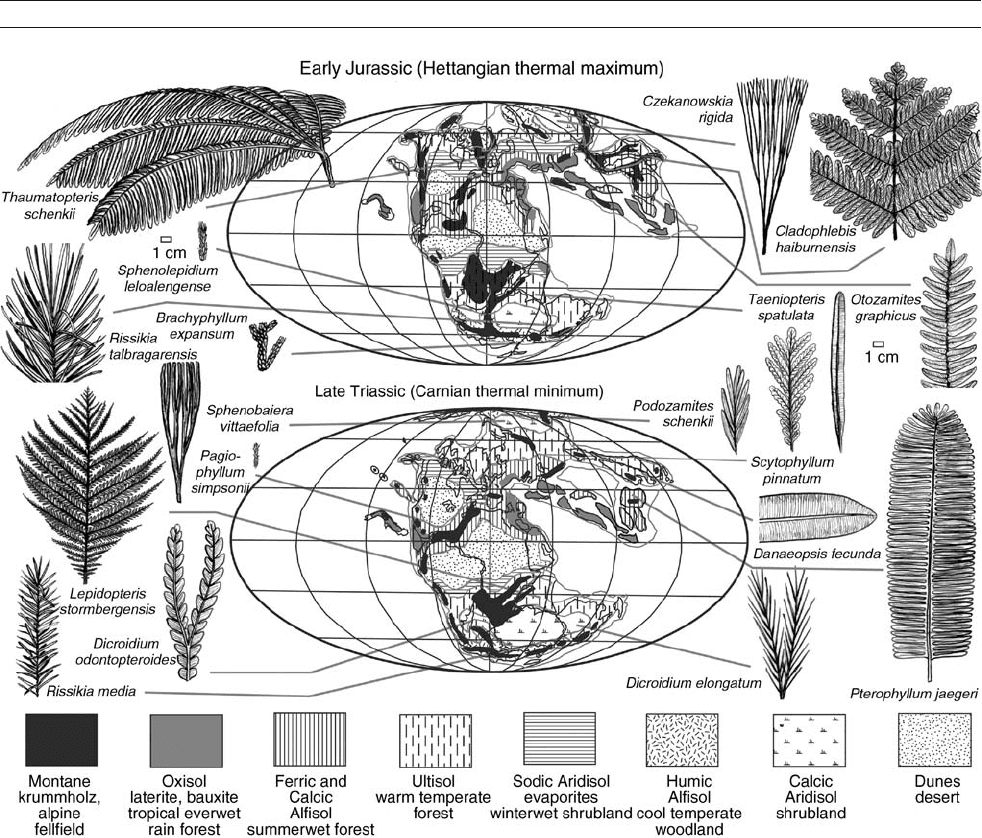
soil-vegetation maps of the late Triassic and early Jurassic

(Figure T18) are in substantial agreement with such maps con-

structed from paleobotanical data alone, or from computer

modeling of potential vegetation (Beerling and Woodward,

2001). Interpreted Triassic and Jurassic plant biomes reveal

no indication of tundra or taiga, and temperate forests extend

within both the Arctic and Antarctic Circles.

Paleosols are evidence not only of regional variation in cli-

mate and vegetation, but also of paleoclimatic changes through

time. The Karoo Basin of South Africa, for example, had sodic-

calcic paleosols (Aridisols) of desertic paleoclimates during

the early Triassic (Scythian Katberg Formation), but by late

Figure T18 Late Triassic (Carnian) and early Jurassic (Hettangian) paleobiogeographic maps and world vegetation inferred from fossil soils and

plants (after Retallack, 1997b, 2002; Willis and McElwain, 2002). Base maps ã C. Scotese.

964 TRIASSIC-JURASSIC CLIMATES