Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

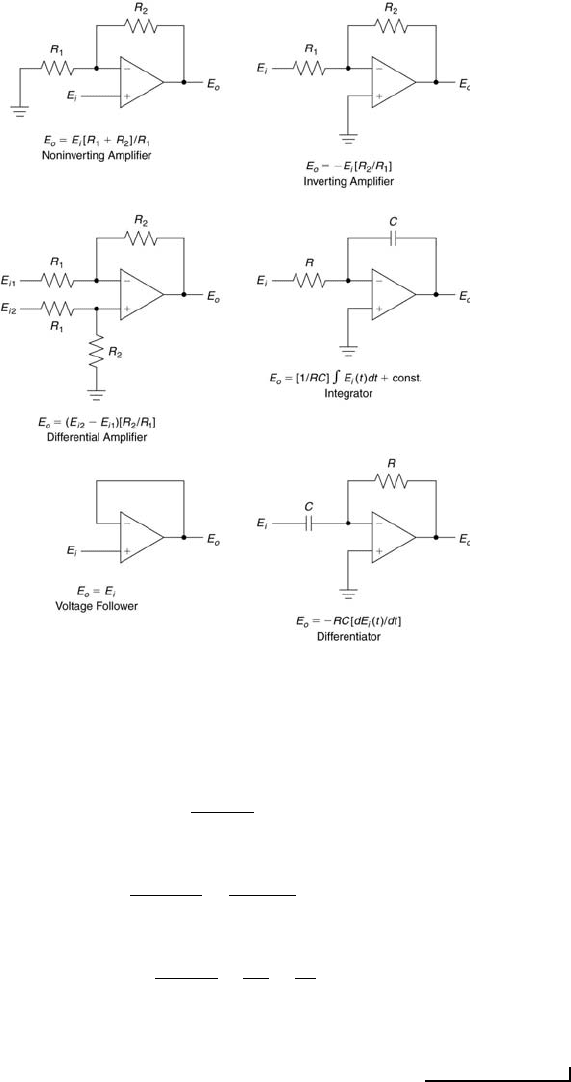
76 Measurement and Data Analysis for Engineering and Science

FIGURE 3.9

Other operational ampliﬁer conﬁgurations.

This implies



+ R



Application of Kirchhoﬀ’s ﬁrst law at node B yields

− E

This gives



+ R





Now E

= E

because of the op amp’s high internal open-loop gain. Equating the

expressions for E

and E

gives the desired result, E

= (E

− E

)(R

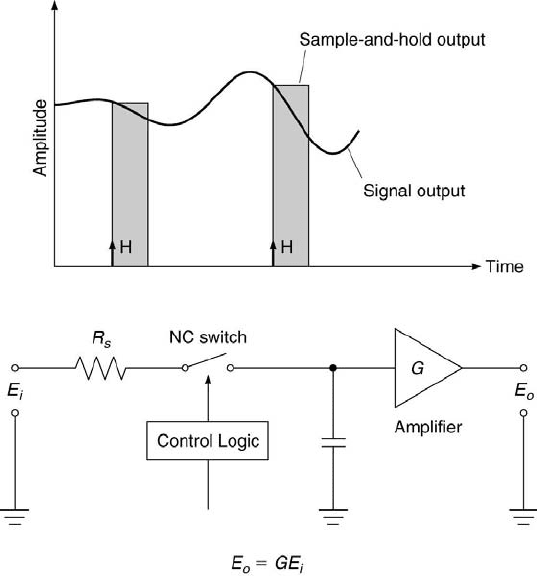
Measurement Systems 77

FIGURE 3.10

The sample-and-hold circuit.

In fact, op amps are the foundations of many signal-conditioning circuits.

One example is the use of an op amp in a simple sample-and-hold circuit, as

shown in Figure 3.10. In this circuit, the output of the op amp is held at a

constant value (= GE

) for a period of time (usually several microseconds)

after the normally-closed (NC) switch is held open using a computer’s logic

control. Sample-and-hold circuits are common features of A/D converters,

which are covered later in this chapter. They provide the capability to si-

multaneously acquire the values of several signals. These values are then

held by the circuit for a suﬃcient period of time until all of them are stored

in the computer’s memory.

Quite often in measurement systems, a diﬀerential signal, such as that

across the output terminals of a Wheatstone bridge, has a small (on the

order of tens of millivolts), DC-biased (on the order of volts) voltage. When

this is the case, it is best to use an instrumentation ampliﬁer. An instru-

mentation ampliﬁer is a high-gain, DC-coupled diﬀerential ampliﬁer with a

single output, high input impedance, and high CMRR [13]. This conﬁgura-

78 Measurement and Data Analysis for Engineering and Science

tion assures that the millivolt-level diﬀerential signal is ampliﬁed suﬃciently

and that the DC-bias and interference-noise voltages are rejected.

3.5 Filters

Another measurement system component is the ﬁlter. Its primary purpose

is to remove signal content at unwanted frequencies. Filters can be passive

or active. Passive ﬁlters are comprised of resistors, capacitors, and induc-

tors that require no external power supply. Active ﬁlters use resistors and

capacitors with operational ampliﬁers, which require power. Digital ﬁltering

also is possible, where the signal is ﬁltered after it is digitized.

The most common types of ideal ﬁlters are presented in Figure 3.11.

The term ideal implies that the magnitude of the signal passing through the

ﬁlter is not attenuated over the desired passband of frequencies. The term

band refers to a range of frequencies and the term pass denotes the unaltered

passing. The range of frequencies over which the signal is attenuated is called

the stopband. The low-pass ﬁlter passes lower signal frequency content up

to the cut-oﬀ frequency, f

, and the high-pass ﬁlter passes content above

. A low-pass ﬁlter and high-pass ﬁlter can be combined to form either a

band-pass ﬁlter or a notch ﬁlter, each having two cut-oﬀ frequencies, f

and f

. Actual ﬁlters do not have perfect step changes in amplitude at

their cut-oﬀ frequencies. Rather, they experience a more gradual change,

which is characterized by the roll-oﬀ at f

, speciﬁed in terms of the ratio of

amplitude change to frequency change.

The simplest ﬁlter can be made using one resistor and one capacitor. This

is known as a simple RC ﬁlter, as shown in Figure 3.12. Referring to the top

of that ﬁgure, if E

is measured across the capacitor to ground, it serves as

a low-pass ﬁlter. Lower frequency signal content is passed through the ﬁlter,

whereas high frequency content is not. Conversely, if E

is measured across

the resistor to ground, it serves as a high-pass ﬁlter, as shown in the bottom

of the ﬁgure. Here, higher frequency content is passed through the ﬁlter,

whereas lower frequency content is not. For both ﬁlters, because they are

not ideal, some fraction of intermediate frequency content is passed through

the ﬁlter. The time constant of the simple RC ﬁlter, τ , equals RC. A unit

balance shows that the units of RC are (V/A)·(C/V) or s. An actual ﬁlter

diﬀers from an ideal ﬁlter in that an actual ﬁlter alters both the magnitude

and the phase of the signal, but it does not change its frequency.

Actual ﬁlter behavior can be understood by ﬁrst examining the case

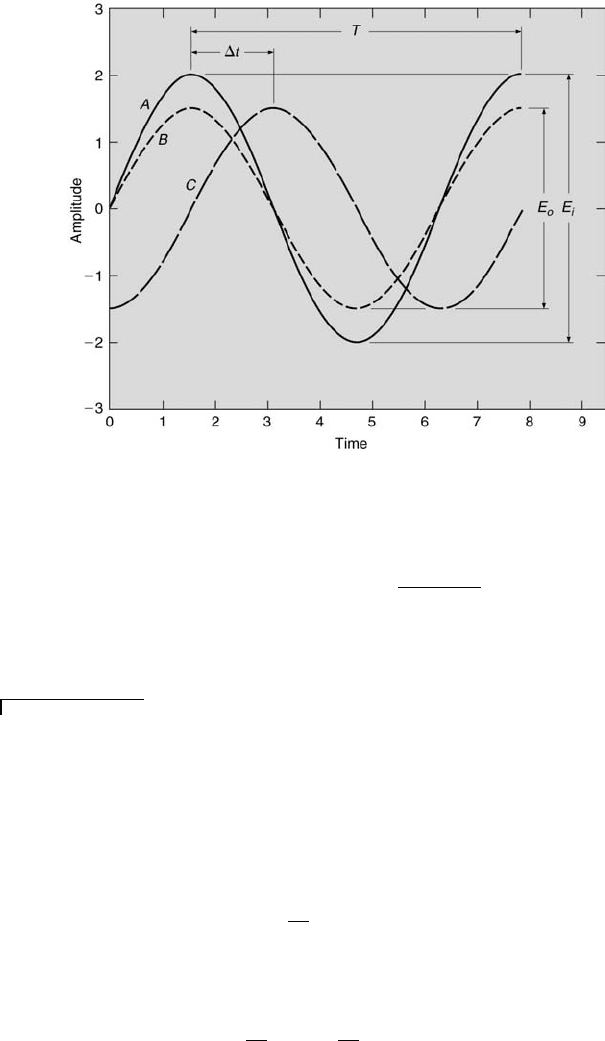
of a simple sinusoidal input signal to a ﬁlter. This is displayed in Figure

3.13. The ﬁlter’s input signal (denoted by A in the ﬁgure) has a peak-to-

peak amplitude of E

, with a one-cycle period of T seconds. That is, the

signal’s input frequency, f, is 1/T cycles/s or Hz. Sometimes the input

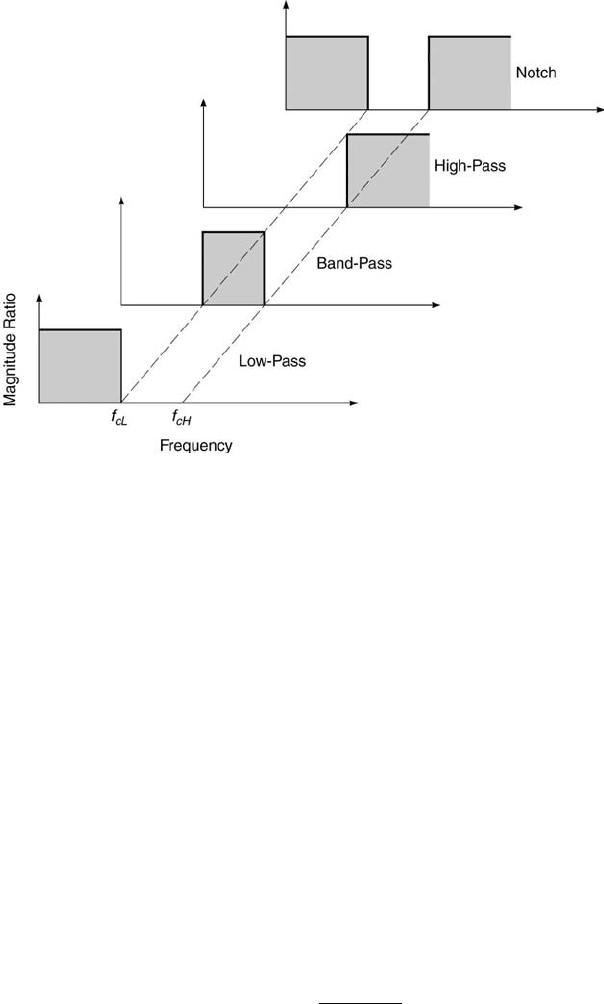
Measurement Systems 79

FIGURE 3.11

Ideal ﬁlter characteristics.

frequency is represented by the circular frequency, ω, which has units of

rad/s. So, ω = 2πf . If the ﬁlter only attenuated the input signal’s amplitude,

it would appear as signal B at the ﬁlter’s output, having a peak-to-peak

amplitude equal to E

. In fact, however, an actual ﬁlter also delays the

signal in time by ∆t between the ﬁlter’s input and output, as depicted by

signal C in the ﬁgure. The output signal is said to lag the input signal by ∆t.

This time lag can be converted into a phase lag or phase shift by noting

that ∆t/T = φ/360

◦

, which implies that φ = 360

◦

(∆t/T ). By convention,

the phase lag equals −φ. The magnitude ratio, M (f), of the ﬁlter equals

(f)/E

(f). For diﬀerent input signal frequencies, both M and φ will have

diﬀerent values.

Analytical relationships for M(f ) and φ(f) can be developed for simple

ﬁlters. Typically, M and φ are plotted each versus ωτ or f/f

, both of which

are dimensionless, as shown in Figures 4.3 and 4.4 of Chapter 4. The cutoﬀ

frequency, ω

, is deﬁned as the frequency at which the power is one-half

of its maximum. This occurs at M = 0.707, which corresponds to ωτ = 1

for ﬁrst-order systems, such as simple ﬁlters [14]. Thus, for simple ﬁlters,

= 1/(RC) or f

= 1/(2πRC). In fact, for a simple low-pass RC ﬁlter,

M(ω) = 1/

1 + (ωτ)

(3.14)

and

φ = −tan

−1

(ωτ). (3.15)

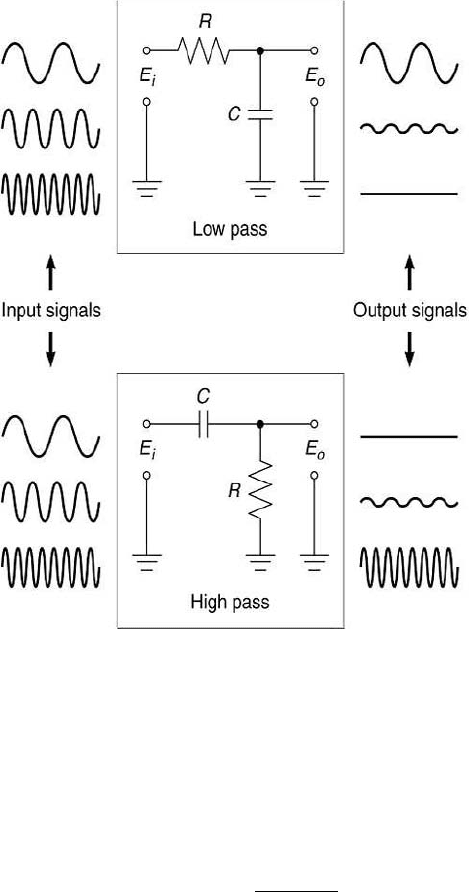
80 Measurement and Data Analysis for Engineering and Science

FIGURE 3.12

Simple RC low-pass and high-pass ﬁlters.

Using these equations, M (ω = 1/τ) = 0.707 and φ = −45

◦

. That is, at

an input frequency equal to the cut-oﬀ frequency of an actual RC low-pass

ﬁlter, the output signal’s amplitude is 70.7 % of the signal’s input amplitude

and it lags the input signal by 45

◦

. For an RC high-pass ﬁlter, the phase

lag equation is given by Equation 3.15 and the magnitude ratio is

M(ω) = ωτ /

1 + (ωτ )

. (3.16)

These equations are derived in Chapter 4.

An active low-pass Butterworth ﬁlter conﬁguration is shown in Figure

3.14. Its time constant equals R

, and its magnitude ratio and phase

lag are given by Equations 3.14 and 3.15, respectively. An active high-pass

Butterworth ﬁlter conﬁguration is displayed in Figure 3.15. Its time constant

equals R

, and its phase lag is given by Equation 3.15. Its magnitude ratio

Measurement Systems 81

FIGURE 3.13

Generic ﬁlter input/output response characteristics.

M(ω) = [R

] · [ωτ/

1 + (ωτ )

]. (3.17)

Other classes of ﬁlters have diﬀerent response characteristics. Refer to [13]

for detailed descriptions or [4] for an overview.

Example Problem 3.5

Statement: For the circuit depicted in Figure 3.14, determine the equation relating

the output voltage E

to the input voltage E

Solution: The op amp’s major attributes assure that no current ﬂows into the op

amp and that the voltage diﬀerence between the two input terminals is zero. Assigning

currents and nodes as shown in Figure 3.14 and applying Kirchhoﬀ’s current law and

Ohm’s law to node 1 gives

= I

Applying Kirchhoﬀ’s current law and Ohm’s law at node 2 results in

= I

+ I

= −

− C

Dividing the above equation through by C

and rearranging terms yields

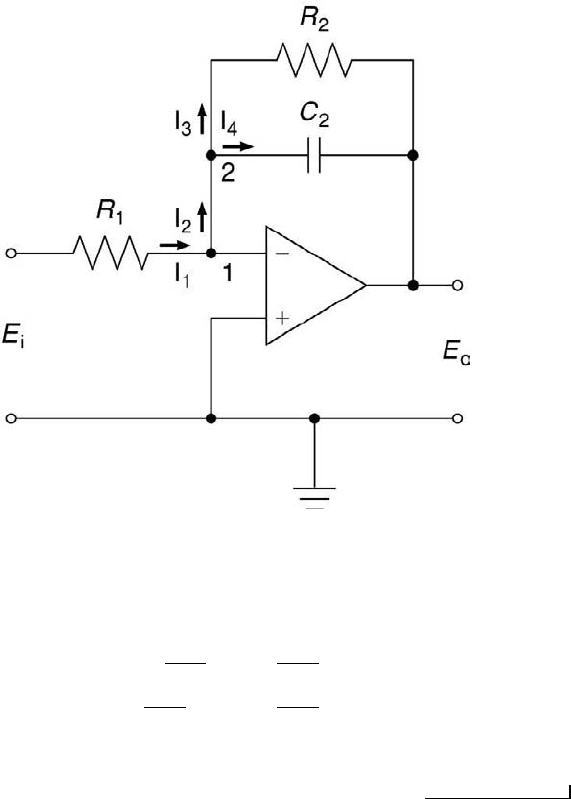
82 Measurement and Data Analysis for Engineering and Science

FIGURE 3.14

The active low-pass Butterworth ﬁlter.

= −

−

= −

This is a ﬁrst-order, ordinary diﬀerential equation whose method of solution is presented

in Chapter 4.

Digital ﬁlters operate on a digitally converted signal. The ﬁlter’s cutoﬀ

frequency adjusts automatically with sampling frequency and can be as

low as a fraction of a Hz [13]. An advantage that digital ﬁlters have over

their analog counterparts is that digital ﬁltering can be done after data has

been acquired. This approach allows the original, unﬁltered signal content to

be maintained. Digital ﬁlters operate by successively weighting each input

signal value that is discretized at equal-spaced times, x

, with k number of

weights, h

. The resulting ﬁltered values, y

, are given by

∞

k=−∞

i−k

. (3.18)

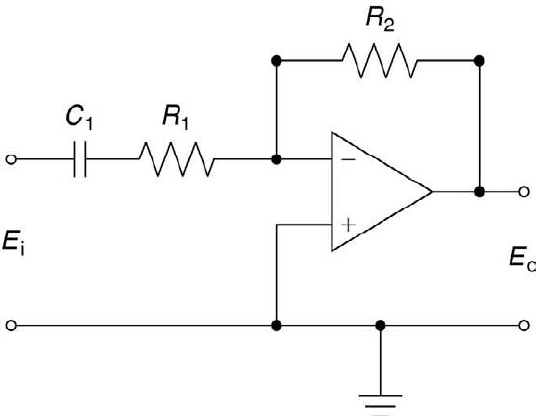
Measurement Systems 83

FIGURE 3.15

The active high-pass Butterworth ﬁlter.

The values of k are ﬁnite for real digital ﬁlters. When the values of h

are

zero except for k ≥ 0, the digital ﬁlter corresponds to a real analog ﬁlter.

Symmetrical digital ﬁlters have h

−k

= h

, which yield phase shifts of 0

◦

180

◦

Digital ﬁlters can use their output value for the i-th value to serve as an

additional input for the (i+1)-th output value. This is known as a recursive

digital ﬁlter. When there is no feedback of previous output values, the ﬁlter

is a nonrecursive ﬁlter. A low-pass, digital recursive ﬁlter [13] can have

the response

= ay

i−1

+ (1 − a)x

, (3.19)

where a = exp(−t

/τ). Here, t

denotes the time between samples and τ the

ﬁlter time constant, which equals RC. For this ﬁlter to operate eﬀectively,

τ >> t

. Or, in other words, the ﬁlter’s cut-oﬀ frequency must be much less

than the Nyquist frequency. The latter is covered extensively in Chapter 10.

An example of this digital ﬁltering algorithm is shown in Figure 3.16. The

input signal of sin(0.01t) is sampled 10 times per second. Three output cases

are plotted, corresponding to the cases of τ = 10, 100, and 1000. Because

of the relatively high sample rate used, both the input and output signals

appear as analog signals, although both actually are discrete. When ωτ is

less than one, there is little attenuation in the signal’s amplitude. In fact,

the ﬁltered amplitude is 99 % of the original signal’s amplitude. Also, the

ﬁltered signal lags the original signal by only 5

◦

. At ωτ = 1, the amplitude

attenuation factor is 0.707 and the phase lag is 45

◦

. When ωτ = 10, the

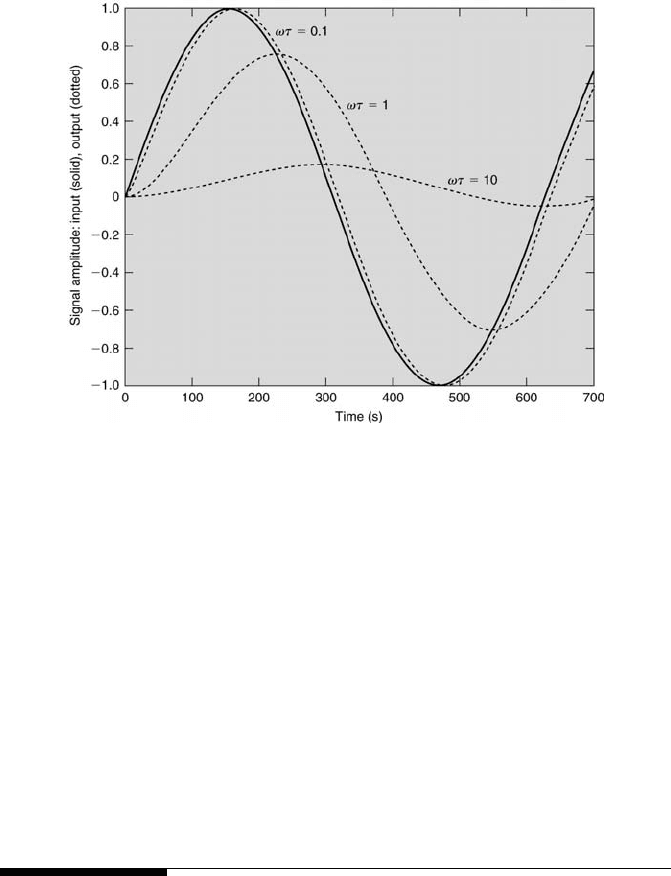
84 Measurement and Data Analysis for Engineering and Science

FIGURE 3.16

Digital low-pass ﬁltering applied to a discretized sine wave.

attenuation factor is 0.90 and the phase lag is 85

◦

. This response mirrors

that of an analog ﬁlter, as depicted in Figure 3.13 and described further in

Chapter 4.

Almost all signals are comprised of multiple frequencies. At ﬁrst, this

appears to complicate ﬁlter performance analysis. However, almost any in-

put signal can be decomposed into the sum of many sinusoidal signals of

diﬀerent amplitudes and frequencies. This is the essence of Fourier analysis,

which is examined in Chapter 9. For a linear, time-invariant system such

as a simple ﬁlter, the output signal can be reconstructed from its Fourier

component responses.

3.6 Analog-to-Digital Converters

The last measurement system element typically encountered is the A/D

converter. This component serves to translate analog signal information into

the digital format that is used by a computer. In the computer’s binary

world, numbers are represented by 0’s and 1’s in units called bits. A bit

value of either 0 or 1 is stored physically in a computer’s memory cell using

a transistor in series with a capacitor. An uncharged or charged capacitor

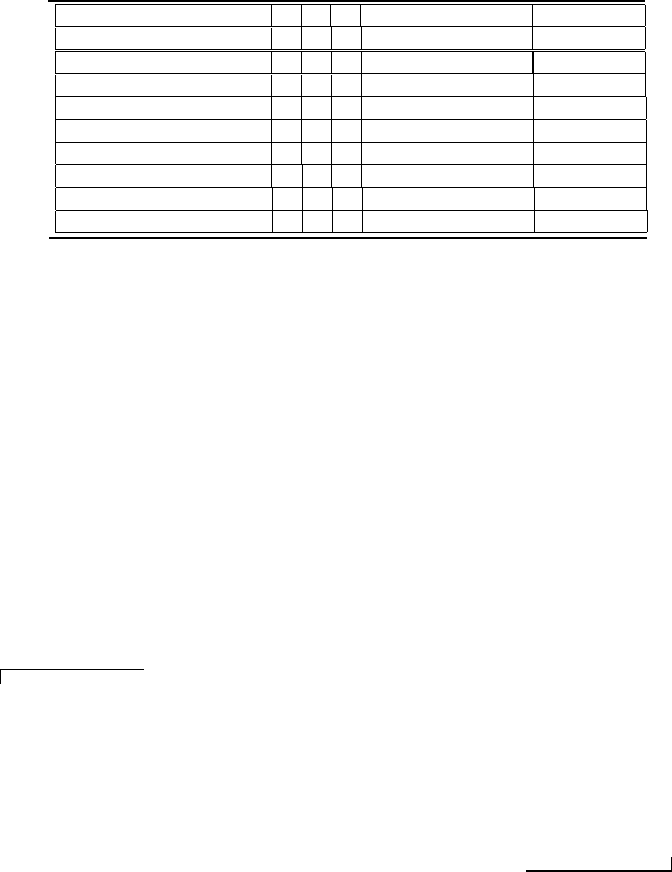
Measurement Systems 85

On Decimal Value

Conversion

Decimal

Oﬀ Decimal Value

Process

Equivalent

Binary Representation

0 · 4 + 0 · 2 + 0 · 1

0 · 4 + 0 · 2 + 1 · 1

0 · 4 + 1 · 2 + 0 · 1

0 · 4 + 1 · 2 + 1 · 1

1 · 4 + 0 · 2 + 0 · 1

1 · 4 + 0 · 2 + 1 · 1

1 · 4 + 1 · 2 + 0 · 1

1 · 4 + 1 · 2 + 1 · 1

TABLE 3.1

Binary to decimal conversion.

represents the value of 0 or 1, respectively. Similarly, logic gates comprised

of on-oﬀ transistors perform the computer’s calculations.

Decimal numbers are translated into binary numbers using a decimal-to-

binary conversion scheme. This is presented in Table 3.1 for a 3-bit scheme.

A series of locations, which are particular addresses, are assigned to a series

of bits that represent decimal values corresponding from right to left to in-

creasing powers of 2. The least signiﬁcant (right-most) bit (LSB) represents

a value of 2

, whereas the most signiﬁcant (left-most) bit (MSB) of an M-bit

scheme represents a value of 2

M−1

. For example, for the 3-bit scheme shown

in Table 3.1, when the LSB and MSB are on and the intermediate bit is oﬀ,

the binary equivalent 101 of the decimal number 5 is stored.

Example Problem 3.6

Statement: Convert the following decimal numbers into binary numbers: [a] 5, [b]

8, and [c] 13.

Solution: An easy way to do this type of conversion is to note that the power of 2 in

a decimal number is equal to the number of zeros in the binary number. [a] 5 = 4 + 1

= 2

+ 1. Therefore, the binary equivalent of 5 is 100 + 1 = 101. [b] 8 = 2

. Therefore,

the binary equivalent of 8 is 1000. [c] 13 = 8 + 4 + 1 = 2

+ 2

+ 1. Therefore, the

binary equivalent of 13 is 1000 + 100 + 1 = 1101.

There are many methods used to perform analog-to-digital conversion

electronically. The two most common ones are the successive-approximation

and ramp-conversion methods. The successive-approximation method

utilizes a D/A converter and a diﬀerential op amp that subtracts the analog

input signal from the D/A converter’s output signal. The conversion pro-

cess begins when the D/A converter’s signal is incremented in voltage steps

from 0 volts using digital logic. When the D/A converter’s signal rises to

within  volts of the analog input signal, the diﬀerential op amp’s output,