Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

86 Measurement and Data Analysis for Engineering and Science

Term

Formula

M = 8

M = 12

MSB Value

M−1

128

2048

LSB Value

Maximum Possible Value

− 1

255

4095

Minimum Possible Value

Number of Possible Values

256

4096

MSB Weight

−1

1/2

LSB Weight

−M

1/256

1/4096

Resolution, Q (mV/bit)

F SR

39.06

2.44

for E

F SR

= 10 V

Dynamic Range (dB)

20 log

(Q/Q

)

−28

−52

Absolute Quantization Error (mV)

±Q/2

±19.53

±1.22

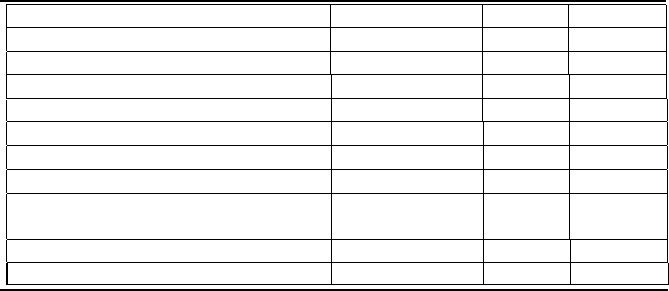
TABLE 3.2

M-bit terminology.

now equal to  volts, causes the logic control to stop incrementing the D/A

converter and tells the computer to store the converter’s digital value. The

ramp-conversion method follows a similar approach by increasing a volt-

age and comparing it to the analog input signal’s voltage. The increasing

signal is produced using an integrating op amp conﬁguration, in which the

op amp conﬁguration is turned on through a switch controlled by the com-

puter. In parallel, the computer starts a binary counter when the op amp

conﬁguration is turned on. When the analog input and op amp conﬁgura-

tion signals are equal, the computer stops the binary counter and stores its

values.

The terminology used for an M-bit A/D converter is summarized in

Table 3.2. The values listed in the table for the LSB and MSB are when

the bit is on. The bit equals 0 when it is oﬀ. The minimum decimal value

that can be represented by the converter equals 0. The maximum value

equals 2

− 1. Thus, 2

possible values can be represented. The weight of

a bit is deﬁned as the value of the bit divided by the number of possible

values. The resolution and absolute quantization error are based on an M-

bit, unipolar A/D converter with a full-scale range (FSR) equal to 10.00

V, where Q

= 1000 mV/bit. Most A/D converters used today are 12-bit

or 16-bit converters, providing signal resolutions of 2.44 mV/bit and 0.153

mV/bit, respectively.

An analog signal is continuous in time and therefore comprised of an

inﬁnite number of values. An M-bit A/D converter, however, can only rep-

resent the signal’s amplitude by a ﬁnite set of 2

values. This presents a

signal resolution problem. Consider the analog signal represented by the

solid curve shown in Figure 3.17. If the signal is sampled discretely at δt

time increments, it will be represented by the values indicated by the open

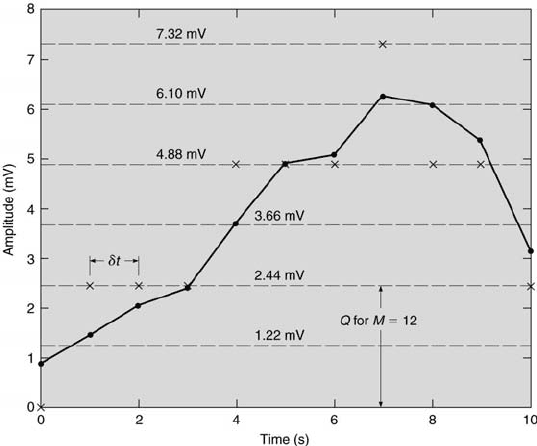
Measurement Systems 87

FIGURE 3.17

Schematic of analog-to-digital conversion.

circles. With discrete sampling, only the signal values between the sample

times are lost, but the signal’s exact amplitude values are maintained at each

sample time. Yet, if this information is stored using the digital sampling

scheme of the A/D converter, the signal’s exact amplitude values also are

lost. In fact, for the 12-bit A/D converter used to sample the signal shown in

Figure 3.17, the particular signal is represented by only four possible values

(0 mV, 2.44 mV, 4.88 mV, and 7.32 mV), as indicated by the ×’s in the

ﬁgure. Thus, a signal whose amplitude lies within the range of ±Q/2 of a

particular bit’s value will be assigned the bit’s value. This error is termed

the absolute quantization error of an A/D converter.

Quite often, if a signal’s amplitude range is on the order of the A/D

converter’s resolution, an ampliﬁer will be used before the A/D converter to

gain the signal’s amplitude and, therefore, reduce the absolute quantization

error to an acceptable level. An alternative approach is to use an A/D board

with better resolution, but, almost always, this is more expensive.

88 Measurement and Data Analysis for Engineering and Science

System

Variable

Sensor/

Signal

no.

(result)

Transducer

Conditioner

Processor

pressure

strain gage,

ampliﬁer,

A/D converter,

(→velocity)

Wheatstone bridge

ﬁlter

computer

force

strain gage,

ampliﬁers,

digital

(→thrust)

Wheatstone bridge

ﬁlter

oscilloscope

pressure

piezoresistive

ampliﬁer

microcontroller

(→velocity)

element

system

acceleration

diﬀerential-capacitive

ampliﬁer

microcontroller

(acceleration)

structure

system

TABLE 3.3

The elements of three measurement systems.

3.7 Example Measurement Systems

The designs of three actual measurement systems are presented in this sec-

tion to illustrate the diﬀerent choices that can be made. The ﬁnal design of

each system involves many trade-oﬀs between the accuracy and the cost of

their components. The elements of each of these systems are summarized in

Table 3.3. Several major diﬀerences can be noted. The most signiﬁcant are

the choices of the sensor/transducer and of the signal processing system.

These are dictated primarily because of the environments in which each is

designed to operate. System 1 is developed to be located near the test sec-

tion of a subsonic wind tunnel, to be placed on a small table, and to use an

existing personal computer. System 2 is designed to be located on one cart

that can be moved to a remote location when the rocket motor is tested.

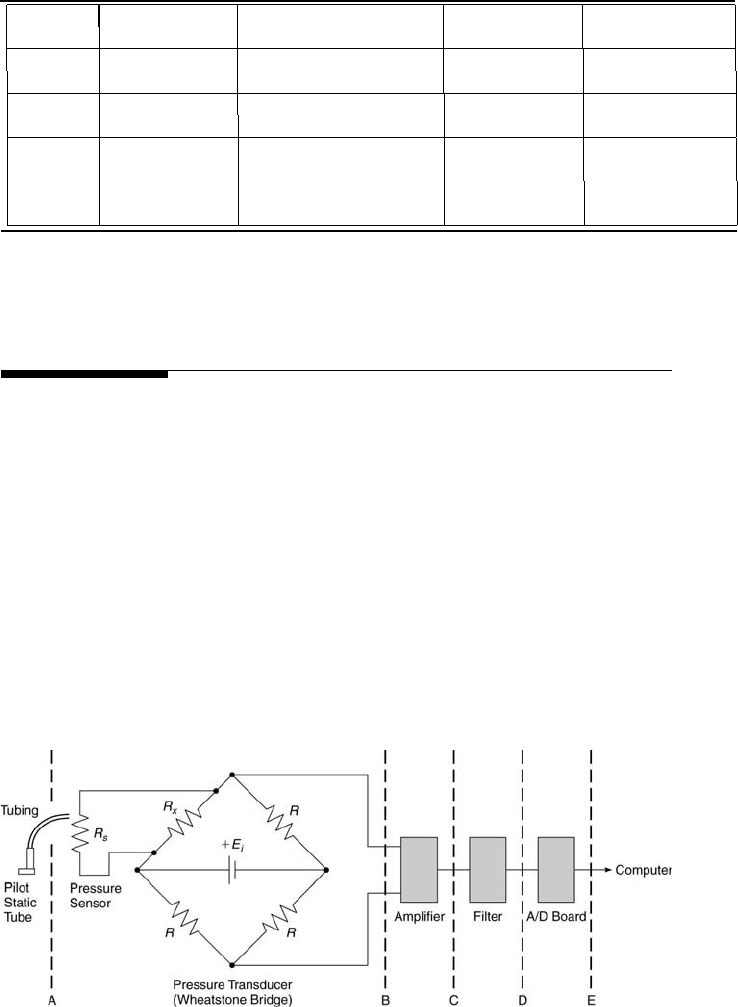
FIGURE 3.18

An example pressure measurement system.

Measurement Systems 89

Component

Conditions

Unknown

Environment

T = 294 K, p = 1 atm

ρ, ∆p, F ,



, δR

Diaphragm



= 0.001 × F , A = 1 cm

, C

= 0.001

Strain Gage

R = 120 Ω at 294 K

Wheatstone Bridge

All R = 120 Ω at 294 K, E

= 5 V

Ampliﬁer

Non-inverting op amp, R

= 1 MΩ

Filter

Low-pass with R = 1 MΩ, C = 1 µF

A/D Converter

F SR

= 10 V, Q < 1 mV/bit

TABLE 3.4

Velocity measurement system conditions.

A digital oscilloscope is chosen for its convenience of remote operation and

its triggering and signal storage capabilities. System 3 is developed to be

placed inside of a 2 in. internal diameter model rocket fuselage and then

launched over 100 m into the air with accelerations and velocities as high as

60 m/s

(∼6 g) and 50 m/s, respectively. These conditions constrain the size

and weight of the measurement system package. A small, battery-powered,

microcontoller-based data acquisition system with an A/D converter, am-

pliﬁer, and memory is designed speciﬁcally for this purpose [15].

Measurement system 1 is designed to measure the velocity of air ﬂowing

in a wind tunnel, as shown in Figure 3.18. Its pitot-static tube is located

within a wind tunnel. The pitot-static tube and tubing are passive and

simply transmit the total and static pressures to a sensor located outside

the wind tunnel. The actual sensor is a strain gage mounted on a ﬂexible

diaphragm inside a pressure transducer housing. The static pressure port is

connected to one side of the pressure transducer’s diaphragm chamber; the

total pressure port to the other side. This arrangement produces a ﬂexure of

the diaphragm proportional to the dynamic pressure (the physical stimulus)

that strains the gage and changes its resistance (the electrical impulse).

This resistance change imbalances a Wheatstone bridge operated in the

deﬂection mode, producing a voltage at station B. Beyond station B, the

signal is ampliﬁed, ﬁltered, converted into its digital format, and ﬁnally

stored by the computer. Another example measurement system, used to

measure temperature, is considered in this chapter’s homework problems.

The velocity measurement system is to be designed such that the input

voltage to the A/D converter, E

, is 10 V when the wind tunnel velocity is

100 m/s. The design also is subject to the additional conditions speciﬁed in

Table 3.4. Given these constraints, the desired input and output character-

istics of each measurement system element can be determined for stations

A through E, as denoted in Figure 3.18. Determination of the performance

characteristics for each stage is as follows:

90 Measurement and Data Analysis for Engineering and Science

• Station A: The velocity, V , of 100 m/s yields a dynamic pressure, ∆p,

of 5700 N/m

using Bernoulli’s equation, ∆p = 0.5ρV

. The density, ρ,

equals 1.14 kg/m

, as determined using Equation 11.1.

• Station B: The dynamic pressure produces a force, F , on the diaphragm,

which has an area, A, equal to 1 cm

. The resulting force is 0.57 N, noting

that the force equals the pressure diﬀerence across the diaphragm times

its area. A longitudinal strain on the diaphragm, 

, is produced by

F , where 

= C

F . The resulting strain is 5.7 × 10

−4

. According to

Equation 3.7, this gives δR/R = 1.14 × 10

−3

. The Wheatstone bridge is

operated in the deﬂection method mode with all resistances equal to 120

Ω at 294 K and V = 0 m/s. The output voltage, E

= E

, is determined

using Equation 2.29 and equals 1.42 mV.

• Station C: The relatively low output voltage from the Wheatstone bridge

needs to be ampliﬁed to achieve the A/D input voltage, E

, of 10 V.

Assuming that the ﬁlter’s magnitude ratio is unity, the gain of the am-

pliﬁer equals E

, which is 10/0.142 or 70.4. An op amp in the

non-inverting conﬁguration is used. Its input-output voltage relation is

given in Figure 3.9. E

= 70.4 and R

= 1 MΩ implies that R

equals 69.4 MΩ.

• Station D: The measurement system operates at steady state. The volt-

ages are DC, having zero frequency. Thus, the ﬁlter’s magnitude ratio

is unity. Therefore, E

= E

• Station E: If the A/D converter has a full scale input voltage, E

F SR

, of

10 V, then the converter is at its maximum input voltage when V = 100

m/s. The relationship between the A/D converter’s E

F SR

, Q, and the

number of converter bits, M, is presented in Table 3.2. Choosing M = 12

does not meet the constraint. The next choice is M = 16. This yields

Q = 0.153 mV/bit, which satisﬁes the constraint.

Many choices can be made in designing this system. For example, the

supply voltage to the Wheatstone bridge could be increased from 5 V to

10 V or 12 V, which are common supply voltages. This would increase

the output voltage of the bridge and, therefore, require less ampliﬁcation

to meet the 10 V constraint. Other resistances can be used in the bridge.

A diﬀerent strain gage can be used on the diaphragm. If the system will

be used for non-steady velocity measurements, then the time responses of

the tubing, the diaphragm, and the ﬁlter need to be considered. Each can

aﬀect the magnitude and the phase of the signal. The ﬁnal choice of speciﬁc

components truly is an engineering decision.

Next, examine measurement system 2 that is designed to acquire thrust

as a function of time of a model rocket motor. The ﬁrst element of the mea-

surement system consists of an aluminum, cantilevered beam with four 120

Ω strain gages, similar to that shown schematically in Figure 2.11. These

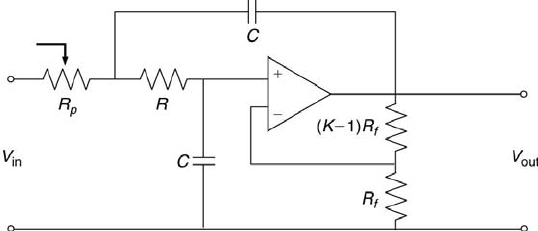
Measurement Systems 91

FIGURE 3.19

Two-pole, low-pass Sallen-and-Key ﬁlter.

strain gages comprise the legs of a Wheatstone bridge. The maximum out-

put of the bridge is approximately 50 mV. So, the output of the bridge is

connected to an instrumentation ampliﬁer with a gain of 100 and then to a

variable-gain, operational ampliﬁer in the inverting conﬁguration. This al-

lows the signal’s amplitude to be adjusted for optimum display and storage

by the digital oscilloscope. A two-pole, low-pass Sallen-and-Key ﬁlter [13]

receives the second ampliﬁer’s output, ﬁlters it, and then passes it to the

digital oscilloscope. The ﬁlter’s schematic is shown in Figure 3.19. Typical

ﬁlter parameter values are R = 200 kΩ, R

= 200 kΩ, C = 0.1 µF, and K

= 1.586. A low-pass ﬁlter is used to eliminate the ∼30 Hz component that

is the natural frequency of the cantilevered beam. The original and ﬁltered

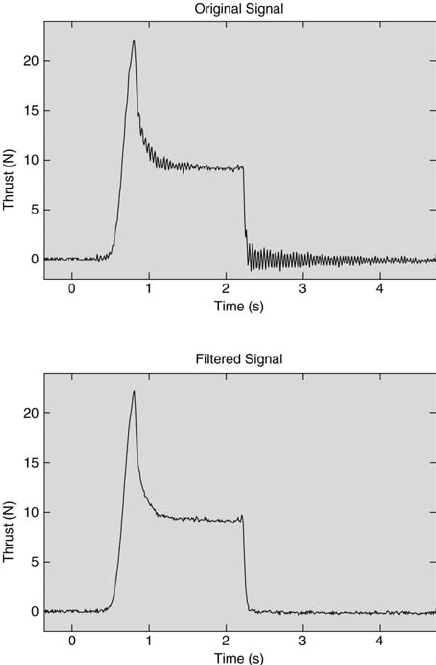
rocket motor thrust data as a function of time are shown in Figure 3.20.

The eﬀect of the low-pass ﬁlter is clearly visible. Additional details about

the experiment can be found on the text web site.

Finally, consider the design of measurement system 3, to be used re-

motely in a model rocket to acquire the rocket’s acceleration and velocity

data during ascent. The measurement system hardware consists of two sen-

sor/transducers, one for pressure and the other for acceleration, and a board

containing a microcontroller-based data acquisition system. The pressure

transducer includes an integrated silicon pressure sensor that is signal condi-

tioned, temperature compensated, and calibrated on-chip. A single piezore-

sistive element is located on a ﬂexible diaphragm. Total and static pressure

ports on the rocket’s nose cone are connected with short tubing to each side

of the ﬂexible diaphragm inside the transducer’s housing. The diﬀerence in

pressure causes the diaphragm to deﬂect, which produces an output voltage

that is directly proportional to the diﬀerential pressure, which for this case is

the dynamic pressure. The single-axis ±5 g accelerometer contains a polysil-

icon surface sensor. A diﬀerential capacitor structure attached to the surface

deﬂects under acceleration, causing an imbalance in its the capacitor circuit.

This produces an output voltage that is linearly proportional to the accel-

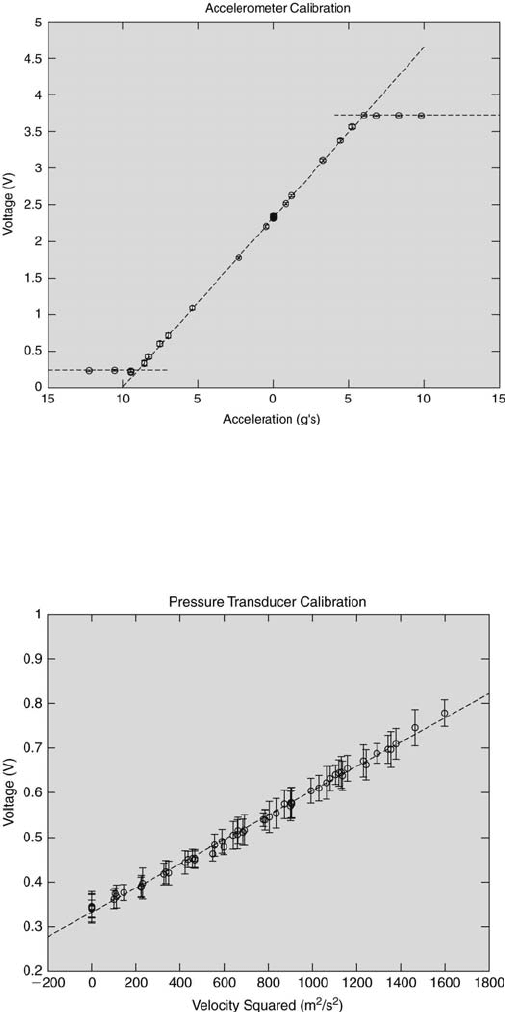
eration. The accelerometer and pressure transducer calibration curves are

92 Measurement and Data Analysis for Engineering and Science

FIGURE 3.20

Original and ﬁltered rocket motor thrust signal.

shown in Figures 3.21 and 3.22, respectively. Both sensor/tranducer outputs

are each routed into an ampliﬁer with a gain of 16 and then to the inputs of

a 12-bit A/D converter. The output digital signals are stored directly into

memory (256 kB). The measurement system board has a mass of 33 g and

dimensions of 4.1 cm by 10.2 cm. The on-board, 3.3 V, 720 mAh Li-battery

that powers the entire system has a mass of 39 g. All of the on-board data

is retrieved after capture and downloaded into a laptop computer. A sample

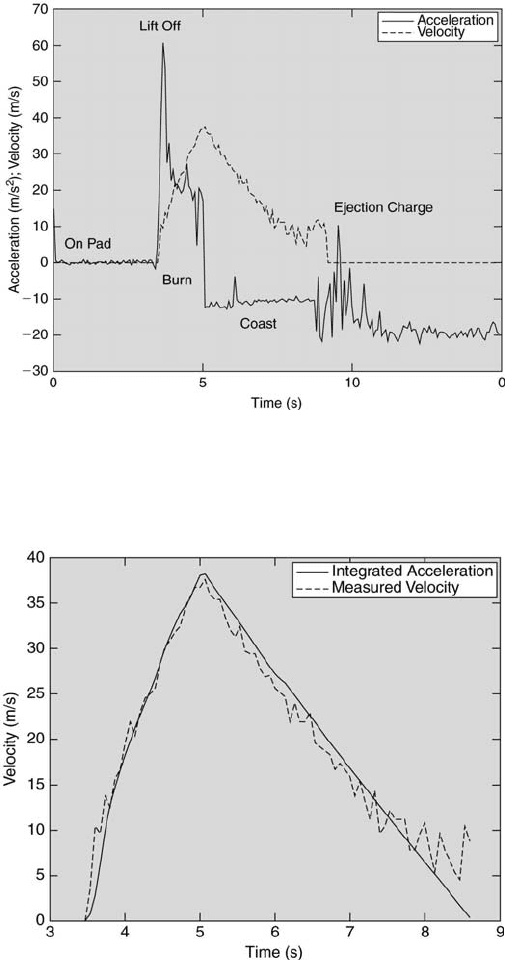
of the reconstructed data is displayed in Figure 3.23 The rocket’s velocity

in time can be determined from the pressure transducer’s output. This is

compared to the time integral of the rocket’s acceleration in Figure 3.24.

Finally, this information can be used with the information on the rocket’s

drag to determine the maximum altitude of the rocket.

Measurement Systems 93

FIGURE 3.21

Calibration of the accelerometer.

FIGURE 3.22

Calibration of the pressure transducer.

94 Measurement and Data Analysis for Engineering and Science

FIGURE 3.23

Example rocket velocity and acceleration data.

FIGURE 3.24

Integrated acceleration and velocity comparison.

Measurement Systems 95

3.8 Problem Topic Summary

Topic

Review Problems

Homework Problems

Components

1, 2, 4, 5, 7

1, 2, 4, 5, 8, 9, 12, 13

Systems

3, 6, 8

3, 6, 7, 10, 11, 14, 15

TABLE 3.5

Chapter 3 Problem Summary

3.9 Review Problems

1. Modern automobiles are equipped with a system to measure the temper-

ature of the radiator ﬂuid and output this temperature to a computer

monitoring system. A thermistor is manufactured into the car radiator.

A conducting cable leads from the thermistor and connects the ther-

mistor to one arm of a Wheatstone bridge. The voltage output from

the Wheatstone bridge is input into the car computer that digitally

samples the signal 10 times each second. If the radiator ﬂuid tempera-

ture exceeds an acceptable limit, the computer sends a signal to light a

warning indicator to alert the driver. Match the following components of

the ﬂuid temperature measurement system (radiator ﬂuid temperature,

thermistor, Wheatstone bridge, and car computer) with their function

in terms of a generalized measurement system (sensor, physical variable,

transducer, and signal processor).

2. Which of the following instruments is used to interface analog systems to

digital ones? (a) A/C converter, (b) D/C converter, (c) A/D converter,

(d) AC/DC converter.

3. A metallic wire embedded in a strain gage is 4.2 cm long with a diameter

of 0.07 mm. The gage is mounted on the upper surface of a cantilever

beam to sense strain. Before strain is applied, the initial resistance of

the wire is 64 Ω. Strain is applied to the beam, stretching the wire 0.1

mm, and changing its electrical resistivity by 2 × 10

−8

Ωm. If Poisson’s

ratio for the wire is 0.342, ﬁnd the change in resistance in the wire due

to the strain to the nearest hundredth ohm.

4. What is the time constant (in seconds) of a single-pole, low-pass, passive

ﬁlter having a resistance of 2 kΩ and a capacitance of 30 µF?