Patrick F. Dunn, Measurement, Data Analysis, and Sensor Fundamentals for Engineering and Science, 2nd Edition

Подождите немного. Документ загружается.

156 Measurement and Data Analysis for Engineering and Science

FIGURE 5.11

Graphical approach to determine p(x)dx.

function. This describes the probability of the number of successful out-

comes, n, in N repeated trials, given that only either success (with proba-

bility P ) or failure (with probability Q = 1 − P ) is possible. The binomial

probability density function, for example, describes the probability of ob-

taining a certain sum of the numbers on a pair of dice when tossed or the

probability of getting a particular number of heads and tails for a series of

coin tosses. The Poisson probability density function models the probability

of rarely occurring events. It can be derived from the binomial probability

density function. Two examples of processes that can be modeled by the

Poisson probability density function are number of disintegrative emissions

from an isotope and the number of micrometeoroid impacts on a spacecraft.

Although the outcomes of these processes are discrete whole numbers, the

process is considered continuous because of the very large number of events

considered. This essentially amounts to possible outcomes that span a large,

continuous range of whole numbers.

Other probability density functions are for continuous processes. The

most common one is the normal (Gaussian) probability density function.

Many situations closely follow a normal distribution, such as the times of

runners ﬁnishing a marathon, the scores on an exam for a very large class,

and the IQs of everyone without a college degree (or with one). The Weibull

probability density function is used to determine the probability of fatigue-

induced failure times for components. The lognormal probability density

Probability 157

function is similar to the normal probability density function but considers

its variable to be related to the logarithm of another variable. The diameters

of raindrops are lognormally distributed, as are the populations of various

biological systems. Most recently, scientists have suggested a new probability

density function that can be used quite successfully to model the occurrence

of clear-air turbulence and earthquakes. This probability density function

is similar to the normal probability density function but is skewed to the

left and has a larger tail to the right to account for the observed higher

frequency of more rarely occurring events.

5.6.1 Binomial Distribution

Consider ﬁrst the binomial distribution. In a repeated trials experiment con-

sisting of N independent trials with a probability of success, P , for an in-

dividual trial, the probability of getting exactly n successes (for n ≤ N) is

given by the binomial probability density function

p(n) =



(N − n)!n!



(1 − P )

N−n

. (5.14)

The mean, ¯n, and the variance, σ

, are N P and N P Q, respectively, where

Q is the probability of failure, which equals 1 −P . The higher-order central

moments of the skewness and kurtosis are (Q −P )/(N P Q)

0.5

and 3 + [(1 −

6P Q)/NP Q], respectively.

As shown in Figure 5.12, for a ﬁxed N, as P becomes larger, the proba-

bility density function becomes skewed more to the right. For a ﬁxed P , as

N becomes larger, the probability density function becomes more symmet-

ric. Tending to the limit of large N and small but ﬁnite P , the probability

density function approaches a normal one. The MATLAB M-ﬁle bipdfs.m

was used to generate this ﬁgure based upon the binopdf(n,N,P) command.

Example Problem 5.4

Statement: Suppose ﬁve students are taking a probability course. Typically, only

75 % of the students pass this course. Determine the probabilities that exactly 0, 1, 2,

3, 4, or 5 students will pass the course.

Solution: These probabilities are calculated using Equation 5.14, where N = 5,

P = 0.75, and n = 0, 1, 2, 3, 4, and 5. They are displayed immediately below and

plotted in Figure 5.13.

p(0) = 1 × 0.75

× 0.25

= 0.0010

p(1) = 5 × 0.75

× 0.25

= 0.0146

p(2) = 10 × 0.75

× 0.25

= 0.0879

p(3) = 10 × 0.75

× 0.25

= 0.2637

p(4) = 5 × 0.75

× 0.25

= 0.3955

p(5) = 1 × 0.75

× 0.25

= 0.2373

sum = 1.0000

158 Measurement and Data Analysis for Engineering and Science

FIGURE 5.12

Binomial probability density functions for various N and P .

5.6.2 Poisson Distribution

Next consider the Poisson distribution. In the limit when N becomes very

large and P becomes very small (close to zero, which implies a rare event) in

such a way that the mean (= NP ) remains ﬁnite, the binomial probability

density function very closely approximates the Poisson probability density

function.

For these conditions, the Poisson probability density function allows us

to determine the probability of n rare event successes (occurrences) out of

a large number of N repeated trial experiments (during a series of N time

intervals) with the probability P of an event success (during a time interval)

as given by the probability density function

p(n) =

(NP )

−NP

. (5.15)

The MATLAB command poisspdf(n,N*P) can be used to calculate the

probabilities given by Equation 5.15. The mean and variance both equal

NP , noting (1 − P ) ≈ 1. The skewness and kurtosis are (NP )

−0.5

and

3 + 1/NP , respectively. As N P is increased, the Poisson probability density

function approaches a normal probability density function.

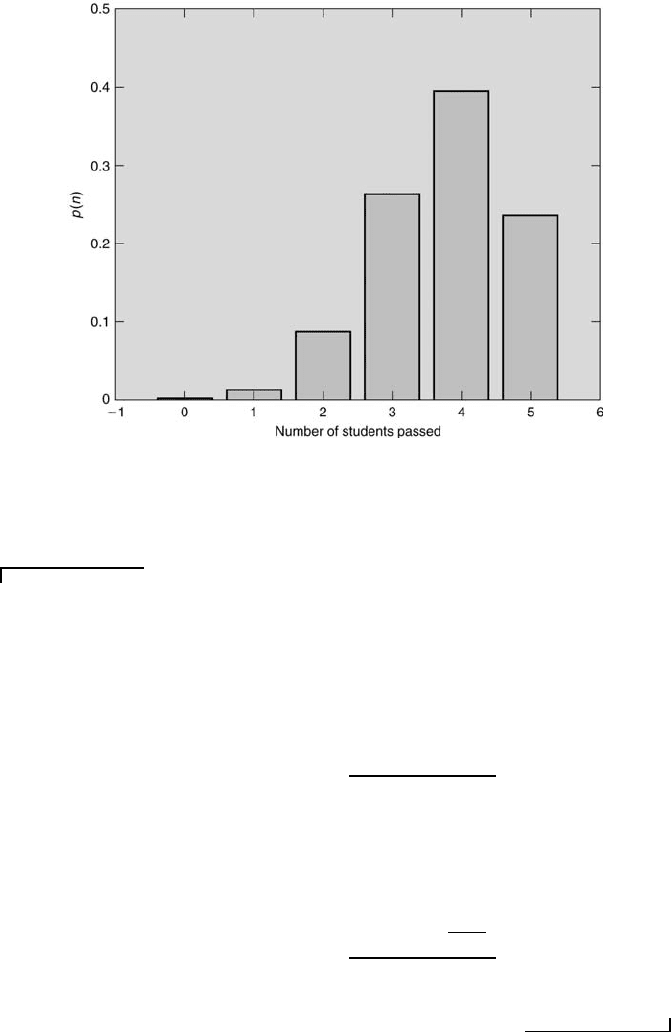
Probability 159

FIGURE 5.13

Probabilities for various numbers of students passed.

Example Problem 5.5

Statement: There are 2 × 10

−20

α particles per second emitted from the nucleus

of an isotope. This implies that the probability for an emission from a nucleus to

occur in one second is 2 × 10

−20

. Assume that the total material to be observed

is comprised of 10

atoms. Emissions from the material are observed at one-second

intervals. Determine the resulting probabilities that a total of 0, 1, 2, ..., 8 emissions

occur in the interval.

Solution: The probabilities are calculated using Equation 5.15, where N = 10

, P

= 2 × 10

−20

and n = 0 through 8. The results are

p(0) = 0.135

p(1) = 0.271

p(2) = 0.271

p(3) = 0.180

p(4) = 0.090

p(5) = 0.036

p(6) = 0.012

p(7) = 0.003

p(8) = 0.001

sum = 0.999

These results are displayed in Figure 5.14.

160 Measurement and Data Analysis for Engineering and Science

FIGURE 5.14

Poisson example of isotope emissions.

5.7 Central Moments

Once the probability density function of a signal has been determined, this

information can be used to determine the values of various parameters.

These parameters can be found by computing the central moments of

the probability density function. Computations of statistical moments are

similar to those performed to determine mechanical moments, such as the

moment of inertia of an object. The term central refers to the fact that

the various statistical moments are computed with respect to the centroid

or mean of the probability density function of the population. The m-th

central moment is deﬁned as

h(x − x

)

i = E [(x − x

)

] = µ

≡

+∞

−∞

(x − x

)

p(x)dx. (5.16)

Either h i or E [ ] denotes the expected value or expectation of the

quantity inside the brackets. This is the value that is expected (in the prob-

abilistic sense) if the integral is performed.

When the centroid or mean, x

, equals 0, the central moments are known

as moments about the origin. Equation 5.16 becomes

Probability 161

i ≡

+∞

−∞

p(x)dx = µ

. (5.17)

Further, the central moment can be related to the moment about the origin

by the transformation

i=0

(−1)





m−i

where





i!(m − i)!

. (5.18)

The zeroth central moment, µ

, is an identity

+∞

−∞

p(x)dx = 1. (5.19)

Having µ

= 1 assures that p(x) is normalized correctly.

The ﬁrst central moment, µ

, leads to the deﬁnition of the mean

value (the centroid of the distribution). For m = 1,



(x − x

)



+∞

−∞

(x − x

)p(x)dx. (5.20)

Expanding the left side of Equation 5.20 yields

h(x − x

)i = hxi − hx

i = hxi − x

= 0, (5.21)

because the expectation of x, hxi, is the true mean value of the population,

. Hence, µ

= 0. Now expanding the right side of Equation 5.20 reveals

that

+∞

−∞

(x −x

)p(x)dx =

+∞

−∞

xp(x)dx −x

+∞

−∞

p(x)dx =

+∞

−∞

xp(x)dx −x

(5.22)

Because the right side of the equation must equal zero, it follows that

+∞

−∞

xp(x)dx. (5.23)

Equation 5.23 is used to compute the mean value of a distribution given its

probability density function.

The second central moment, µ

, deﬁnes the variance, σ

, as

+∞

−∞

(x − x

)

p(x)dx = σ

, (5.24)

which has units of x

. The standard deviation, σ, is the square root of

the variance. It describes the width of the probability density function.

162 Measurement and Data Analysis for Engineering and Science

The variance of x can be expressed in terms of the expectation of x

E[x

], and the square of the mean of x, x

. Equation 5.16 for this case

becomes

= E[(x − x

)

]

= E[x

− 2xx

+ x

]

= E[x

] − 2x

E[x] + x

= E[x

] − 2x

+ x

= E[x

] − x

. (5.25)

So, when the mean of x equals 0, the variance of x equals the expectation

of x

. Further, if the mean and variance of x are known, then E[x

] can be

computed directly from Equation 5.25.

Example Problem 5.6

Statement: Determine the mean power dissipated by a 2 Ω resistor in a circuit

when the current ﬂowing through the resistor has a mean value of 3 A and a variance

of 0.4 A

Solution: The power dissipated by the resistor is given by P = I

R, where I is

the current and R is the resistance. The mean power dissipated is expressed as E[P ].

Assuming that R is constant, E[P ] = E[I

R] = RE[I

]. Further, using Equation 5.25,

E[I

] = σ

+ I

. So, E[P ] = R(σ

+ I

) = 2(0.4 + 3

) = 18.8 W. Expressed with the

correct number of signiﬁcant ﬁgures (one), the answer is 20 W.

The third central moment, µ

, is used in the deﬁnition of the skew-

ness, Sk, where

Sk =

+∞

−∞

(x − x

)

p(x)dx. (5.26)

Deﬁned in this manner, the skewness has no units. It describes the symme-

try of the probability density function, where a positive skewness implies

that the distribution is skewed or stretched to the right. This is shown in

Figure 5.15. When the distribution has positive skewness, the probability

density function’s mean is greater than its mode, where the mode is the

most frequently occurring value. A negative skewness implies the opposite

(stretched to the left with mean < mode). The sign of the mean minus

the mode is the sign of the skewness. For the normal distribution, Sk = 0

because the mean equals the mode.

The fourth central moment, µ

, is used in the deﬁnition of the kur-

tosis, Ku, where

Ku =

+∞

−∞

(x − x

)

p(x)dx, (5.27)

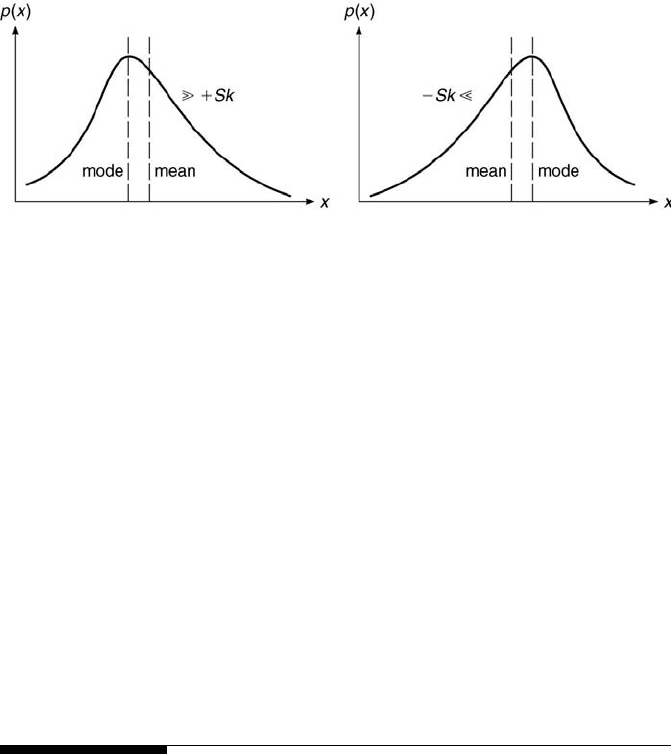
Probability 163

FIGURE 5.15

Distributions with positive and negative skewness.

which has no units. The kurtosis describes the peakedness of the probability

density function. A leptokurtic probability density function has a slender

peak, a mesokurtic one a middle peak, and a platykurtic one a ﬂat peak.

For the normal distribution, Ku = 3. Sometimes, another expression is

used for the kurtosis, where Ku

∗

= Ku − 3 such that Ku

∗

< 0 implies

a probability density function that is ﬂatter than the normal probability

density function, and Ku

∗

> 0 implies one that is more peaked than the

normal probability density function.

For the special case in which x is a normally distributed random variable,

the m-th central moments can be written in terms of the standard deviation,

where µ

= 0 when m is odd and > 1, and µ

= 1 · 3 · 5 · · · (m − 1)σ

when m is even and > 1. This formulation obviously is useful in determining

higher-order central moments of a normally distributed variable when the

standard deviation is known.

5.8 Probability Distribution Function

The probability that a value x is less than or equal to some value of x

∗

deﬁned by the probability distribution function, P (x). Sometimes this

also is referred to as the cumulative probability distribution function. The

probability distribution function is expressed in terms of the integral of the

probability density function

P (x

∗

) = P r[x ≤ x

∗

] =

∗

−∞

p(x)dx. (5.28)

From this, the probability that a value of x will be between the values of x

∗

and x

∗

becomes

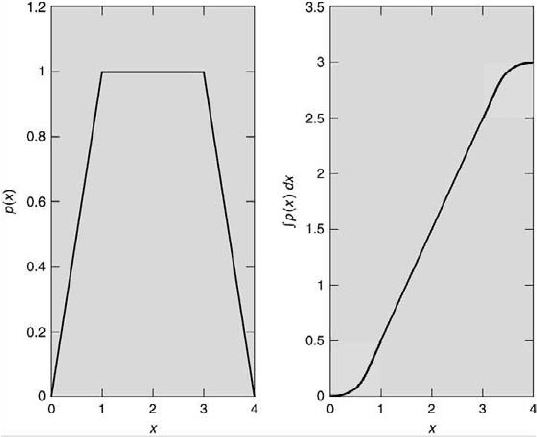
164 Measurement and Data Analysis for Engineering and Science

FIGURE 5.16

Example probability density (left) and probability distribution (right) func-

tions.

P r[x

∗

≤ x ≤ x

∗

] = P (x

∗

) − P (x

∗

) =

∗

p(x)dx. (5.29)

Note that p(x) is dimensionless. The units of P (x) are those of x.

Example plots of p(x) and P (x) are shown in Figure 5.16. The probability

density function is in the left ﬁgure and the probability distribution function

in the right ﬁgure. The P(x) values for each x value are determined simply

by ﬁnding the area under the p(x) curve up to each x value. For example,

the area at the value of x = 1 is a triangular area equal to 0.5 × 1.0 ×

1.0 = 0.5. This is the corresponding value of the probability distribution

function at x = 1. Note that the probability density in this example is not

normalized. The ﬁnal value of the probability distribution function does

not equal unity. What does the maximum value of the probability density

function have to be for the probability density function to be normalized

correctly, as described in Section 5.7? The answer is unity. So, to normalize

p(x) correctly, all values of p(x) should be divided by 1/3 in this example.

Probability 165

5.9 *Probability Concepts

The concept of the probability of an occurrence or outcome is intuitive.

Consider the toss of a fair die. The probability of getting any one of the

six possible numbers is 1/6. Formally this is written as P r[A] = 1/6 or

approximately 17 %, where the A denotes the occurrence of any one speciﬁc

number. The probability of an occurrence can be deﬁned as the number of

times of the occurrence divided by the total number of times considered (the

times of the occurrence plus the times of no occurrence). If the probabilities

of getting 1 or 2 or 3 or 4 or 5 or 6 on a single toss are added, the result is

P r[1]+P r[2]+P r[3]+P r[4]+P r[5]+P r[6] = 6(1/6) = 1. That is, the sum of

all of the possible probabilities is unity. A probability of 1 implies absolute

certainty; a probability of 0 implies absolute uncertainty or impossibility.

Now consider several tosses of a die and, based upon these results, de-

termine the probability of getting a speciﬁc number. Each toss results in an

outcome. The tosses when the speciﬁc number occurred comprise the set

of occurrences for the event of getting that speciﬁc number. The tosses in

which the speciﬁc number did not occur comprise the null set or comple-

ment of that event. Remember, the event for this situation is not a single

die toss, but rather all the tosses in which the speciﬁc number occurred. Sup-

pose, for example, the die was tossed eight times, obtaining eight outcomes:

1, 3, 1, 5, 5, 4, 6, and 2. The probability of getting a 5 based upon these

outcomes would be P r[5] = 2/8 = 1/4. That is, two of the eight possible

outcomes comprise the set of events where 5 is obtained. The probability of

the event of getting a 3 would be P r[3] = 1/8. These results do not imply

necessarily that the die is unfair, rather, that the die has not been tossed

enough times to assess its fairness. This subject was considered brieﬂy (see

Equation 5.2). It addresses the question of how many measurements need

to be taken to achieve a certain level of conﬁdence in an experiment.

5.9.1 *Union and Intersection of Sets

Computing probabilities in the manner just described is correct provided the

one event that is considered has nothing in common with the other events.

Continuing to use the previous example of eight die tosses, determine the

probability that either an even number or the numbers 3 or 4 occur. There is

P r[even] = 3/8 (from 4, 6, and 2) and P r[3] = 1/8 and P r[4] = 1/8. Adding

the probabilities, the sum equals 5/8. Inspection of the results, however,

shows that the probability is 1/2 (from 3, 4, 6, and 2). Clearly the method

of simply adding these probabilities for this type of situation is not correct.

To handle the more complex situation when events have members in

common, the union of the various sets of events must be considered, as

illustrated in Figure 5.17. The lined triangular region marks the set of events