Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

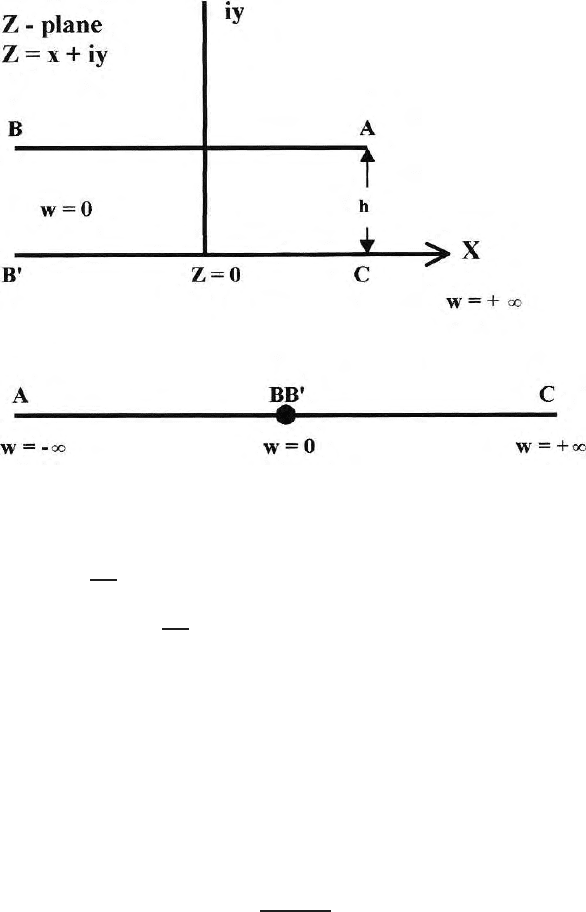
9.6 Geophysical Problems on S-C Transformation 279

Fig. 9.8. ( a) S-C transformation of a horizontal overburden of uniform thichness

over a resistive basement in the Z plane; (b) Map on to the real axis of the W plane

=A(w− 0)

−π/π

because w = 0 at BB

′

(9.75)

dz = A

z=A1nw+C

(9.76)

This is the transformation function which maps the z = x + iy plane onto

the real axis of the w = u + iν plane. Now to solve the problem completely

we hav e to determine ‘A’ and ‘C

’. The constant ‘A’ can be determined as

follows. As we move from A

′

to C

′

over a large semicircle from π to 0, the

movement in the z-plane is – ‘ih’, where ‘h’ is the thickness of the substratum

and the vertical axis is the imaginary axis.

Let w = Re

iθ

.AsR→∞the (9.75) reduces to the form

−ih = A



iRe

iθ

dθ

iθ



idθ (9.77)

A=h/π

We can choose the origin in such a way that the constant of integration

becomes zero. If we choo se z = 0 at w = 1. Then C

= 0. And our origin

is ﬁxed at w = 1. Therefore,

280 9 Complex Variables and Conformal Transformation in Poten tial Theory

ln w (9.78)

and

u=e

πx/h

. cos (πy/h) (9.79)

ν =e

πx/h

. sin (πy/h) . (9.80)

Position of the current source I is u = −1, and potential in the w-plane φ

given by

Iρ

(9.81)

where r is the distance between the position of the source and the point of

measurement. In the w-plane

r={(u + l)

+ ν

}

1/2

therefore

= −

Iρ

2π



(u + l)

+ ν



In the z plane

= −

Iρ

2π



2πx/h

+2.e

πx/h

cos (πy/h) + l



. (9.82)

For y = h

= −

Iρ

2π



2πx/h

+2.e

πx/h



(9.83)

Iρ



πx/h

− 1



. (9.84)

9.6.2 Problem 2 Telluric Field over a Vertical Basement Fault

The geometry of the problem is shown is Fig. (9.9 a, b,). The problem was

solved independently by Kunetz and de Gery (1956), Berdichevsku, M.N.

(1950), Li. Y. Shu (1963). Here the basement is assumed to be vertically

faulted. The thicknesses of the sedimentary layer on the downthrow and

upthrow sides are ‘H’ a n d ‘h’ respectively. ρ

, the resistivity of the sedimen-

tary column, is assumed to be unity. ρ

, the resistivity of the basement, is

considered to be inﬁnitely high (ρ

= ∞). Since the areas adjacent to the

fault planes are suitable sites for oil accumulation, telluric current method is

used as a reconnaissance to ol for location of these fault planes.

Telluric currents or earth currents originate due to interaction of the

earth’s natural electromagnetic ﬁeld with the earth’s crust. Earth’s natu-

ral electromagnetic ﬁeld originates due to interaction of the solar ﬂares with

the magnetosphere of the earth. Telluric current sources are assumed to be

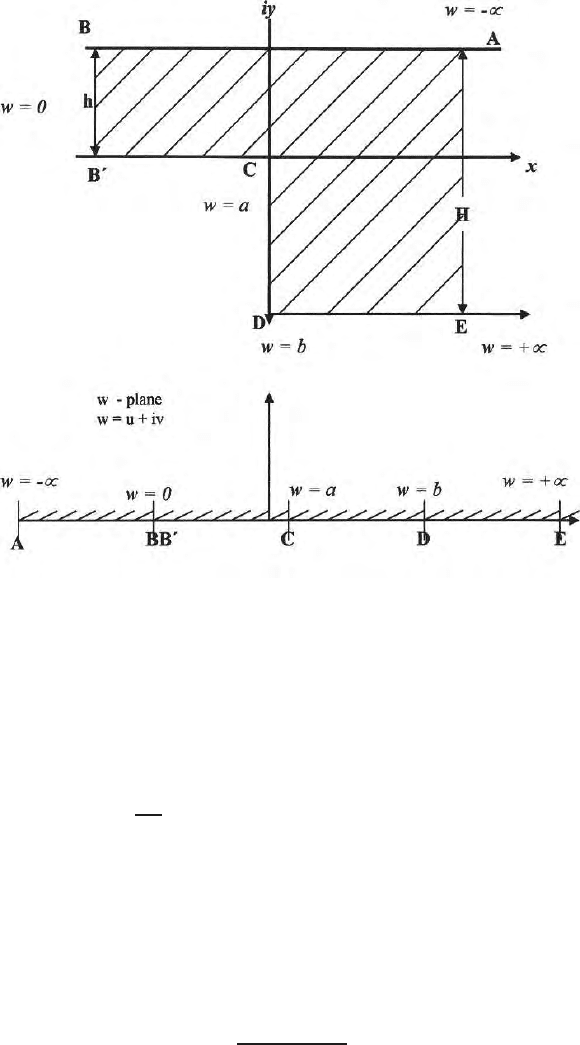
9.6 Geophysical Problems on S-C Transformation 281

Fig. 9.9. (a) S - C Transformation of a vertical fault type of structure in the plane;

(b) Map on to the real axis of the W plane

inﬁnitely long line current sources placed at inﬁnity such that uniform ﬁeld is

created.

The Schwarz-Christoﬀel transformation function, which maps the struc-

ture in the z-plane onto the real axis of the w-plane, is given by

=Aw

−1

(w −a)

1/2

(w − b)

−1/2

(9.85)

because the corners crossed are a t BB’, C and D; the correspon di ng angles are

π, −π/

and +π/

. The change in angles at C and D are π/

in both cases.

At the point C the movement is away from the polygon and at the p oint D

the movement is towards the polygon. Hence there will be change in sign at

C and D. This step is important to get the starting integral correctly before

SC transformation starts.

Here

z=A



(w −a)

1/2

w(w− b)

1/2

dw + C

(9.86)

282 9 Complex Variables and Conformal Transformation in Poten tial Theory

where A is a constant to be determined. Applying the ﬁrst boundary condition,

i.e. we integrate the (9.86) over a large semicircle of radius R(→∞)asw

changes from −∞ to + ∞ and θ varies from 0 to π. The movement in the

z-plane is – iH. Therefore, we have

−iH = A





iθ

− a



iθ



iθ

− b



iRe

iθ

dθ. (9.87)

Since R is inﬁnitely large, (9.87) reduces to the form

−iH = A





iθ



iθ



iθ



iRe

iθ

dθ

. (9.88)

We next apply the second bound ary condition i.e. we integrate (9.86) over an

inﬁnitesimal semicircle around BB’ with w = re

iθ

where r → 0andθ varies

from π to 0. The movement in the z-plane is –ih. Hence

−ih =





iθ

− a



1/2

iθ



iθ

− b



1/2

iRe

iθ

dθ



idθ

. (9.89)

Since in this problem one of the values of a or b can be chosen arbitra rily.

We choose the value of a = 1, therefore

√

. (9.90)

The integral (9.86) can be solved with the substitution of

w − 1

w − b

sincea=1,wecanwrite



(w − 1)

1/2

w(w− b)

1/2



(1 −b) dt

− 1)



− 1



(9.91)

9.6 Geophysical Problems on S-C Transformation 283

because

− 1

and

dw =

2t (1 − b)

− 1)

The integral can be solved by the well known method of partial fraction and

it reduces to the form

)

√

bt −1

√

bt + 1

+ln

1+t

1 −t

(9.92)

)

√

w − 1 −

√

w − b

√

w − 1+

√

w − b

+ln

√

w − b+

√

w −1

√

w − b −

√

w −1

. (9.93)

Equation (9.93) is the required mapping function for transformation of the

geometry from the z-plane to the w-plane. Now in order to determine the

value of C

, we ﬁx the origin in the z-plane at w = 1. Fixing the origin within

the prescribed geometry of the z-plane is at our disposal. We can ﬁx the origin

at any point we want. Now if z = 0 at w = 1, we get from (9.93).



√

ln (−1) + ln (1)



√

.iπ

= −i

√

= −ih. (9.94)

Computation of Telluric Field

In order to compute the telluric ﬁeld, the source and sink are assumed to be

at inﬁnity. The source is at z = −∞, at w = 0 and the sink is at z = +∞,

and w = −∞, the expression for the telluric ﬁeld in given by

φ =

Iρ

. (9.95)

Since the source and sink are assumed to be the inﬁnitely long line electrodes,

therefore

dφ

= −

Iρ

(9.96)

The expression for the telluric ﬁeld in the z-plane is

dφ

284 9 Complex Variables and Conformal Transformation in Poten tial Theory

dφ

. (9.97)

Since the measurements are taken on the surface and on the real axis of the

wplaneν = 0, therefore

. (9.98)

Again for a particular geometry of the structure y = const ≡ ih and dz = dx.

Therefore telluric ﬁeld can be computed from the (9.97) where the expressions

for

dφ

and

are known.

9.6.3 Problem 3 Telluric Field and Apparent Resistivity

Over an Anticline

This is also a similar type of boundary value problem a s discussed in the

previous section i.e., in connection with ﬂow of telluric currents over basement

structure. Important points to be highlighted are: (i) close form solution of

this problem is not possible, therefore one has to use numerical methods for

solution of a part of this problem (i i) movements in the complex plane from

thetipoftheanticlineandthetrajectory of movement are demonstrated .

A two dimensional model of an anticline is shown in (Fig. 9.11 a,b) ECABD

is the inﬁnitely resistive basement and D

′

is the earth surface. The domain

delineated by the polygonal boundary ECABD D

′

is ﬁlled with a medium

of ﬁnite resistivity (ρ = 1). Telluric currents, far away from the structure, are

assumed to be horizontal current sheets conﬁned to the channel bounded by

the surface and the basement. The thickness of the overburden, away from

the structure, is assumed to be unity. (Roy a nd Naidu 1970).

Potential distribution in a homogeneous and isotropic medium and in a

source free region is given by the Laplace’s equation

∂

φ (x, y)

∂x

∂

φ (x, y)

∂y

=0. (9.99)

The method of Schwarz-Christoﬀel transformation is used for conformal map-

ping. The transformation maps the complex geometry of the problem onto a

simple geometry consisting of whole of the positive w-plane and the boundary

along the u-axis while keeping the Laplace’s equation and the boundary con-

ditions invariant. Since ECABD D

′

is a ﬁve cornered polygon, there will be

ﬁvetermsofthetype(w− a

)

−a

/π

where n = 1 ......5, out of which three

may be chosen arbitrarily. The choices are as follows (9.10 a,b)

= ±∞ (Corresponding to EE

′

)

= −k (Corresponding to C)

= 0 (Corresponding to A

= 1 (Corresponding to B)

= 1 (Corresponding to DD

′

)

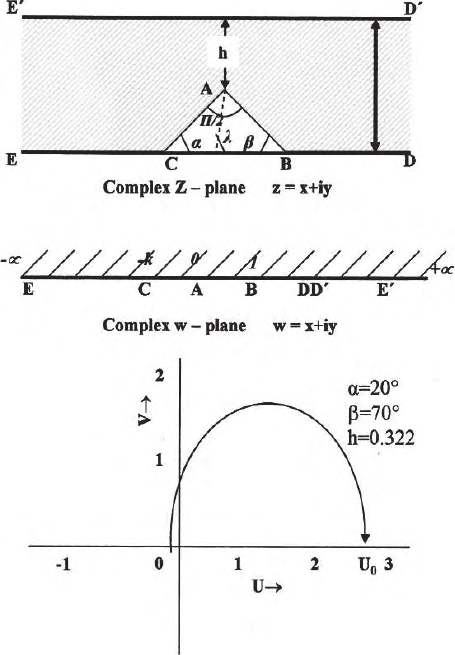
9.6 Geophysical Problems on S-C Transformation 285

(a)

(b)

(c)

Fig. 9.10. (a) Map of the basement asymmetric anticline in the Z plane; (b)its

map onto the real axis of the W plane; (c) trajectory in the W plane of vertical

mo vement from the tip of the anticle A to the epicentre of A on the surface in the

Zplane

and the arguments α

, α

are given as follows

= π (Corresponding to EE

′

)

= α (Corresponding to C)

= −(α + β) (Corresponding to A)

= β (Corre sponding to B)

= π (Corresponding to DD

′

)

Hence the Schwarz – Christoﬀel transformation function for the present prob-

lem may be expressed in the diﬀerential form as

286 9 Complex Variables and Conformal Transformation in Poten tial Theory

α+β

(w + k)

−α/π

(w − l)

−β/π

(w − l)

−1

(9.100)

which can be rewritten as

z=A



α+β

(w + k)

α/π

(w − l )

β/π

(w − l)

+C. (9.101)

The term corresponding to the point EE

′

does not enter into the diﬀeren-

tial equation because the value of w at E and E

′

are ±∞. The constant of

integration is C = 0 because the origin i n the z-plane is ﬁxed.

The evaluations of the unknowns A

,...k are attempted using the follow-

ing boundary conditions. Equation (9.101) is integrated at a point A along a

semiinﬁnite circle in the upper half of the w-plane. Substituting w = Re

iθ

and

R →∞.

One gets

z=A





iθ



α+β

iRe

iθ

dθ



iθ



α/π



iθ

− l



β/π



iθ

− l



(9.102)

By moving in an inﬁnitely large semicircle from to 0 to π along the upper half

of the w-plane, the corresponding movement in the z-plane is from E to E

′

i.e. ‘iH’ where ‘H’ is the thickness of the overburden (assumed to be unity).

So z = iH = i

As R →∞the integral reduces to

i=A



idθ or A

= −

. (9.103)

Next the (9.101) is integrated along an inﬁnitesimal semicircle ar ound DD

′

the upper half of the w-plane. Substituting w = 1 + re

iθ

as r → 0, one gets

z=A





1+re

iθ



α+β

ire

iθ

dθ

(1 + re

iθ

+k)

α/π

(1 + re

iθ

− ℓ)

β/π

(1 + re

iθ

− 1)

i=A



idθ

(1 + k)

α/π

(1 −ℓ)

β/π

because movement in the z-plane is from D to D

′

which is ‘iH’ or simply ‘i’.

Therefore

(1 + k)

α/π

(1 −1)

β/π

− iπ

9.6 Geophysical Problems on S-C Transformation 287

k=(1−ℓ)

β/α

− 1. (9.104)

One more equation is required to solve for ‘k’ and ‘1’ uniquely. The following

procedure is adopted. The inverse of the (9.98) is written as

−1

−(α+β)

(w + k)

α/π

(w − ℓ)

β/π

(w − 1) . (9.105)

A solution of the diﬀerential equation in a closed form is not possible

except when both α/π and β/π can be expressed as ratio of two integers.

Hence (9.105) has to be solved numerically.

Since

− i

One gets

=+Real



−(α+β)

(w + k)

α/π

(w − ℓ)

β/π

(w −1)



(9.106)

=+Imag



−(α+β)

(w + k)

α/π

(w − ℓ)

β/π

(w − 1)



. (9.107)

Values of ‘k’ and ‘1’ are selected and the system of (9.106) and (9.107) are

integrated from y = 0 to y = h keeping x constant (here x = 0). While

integrating numerically the point in the w-plane describes a trajectory which

commences at the origin and ends somewhere on the positive part of the

real axis (Fig. 9.11c). This point represents the projection of the vertex of

the triangle, it is termed as ‘epicentre’ U

. Of course, the initial condition

is u = v = 0 when y = 0. But at this point the integrands (9.106) and

(9.107) are singular. They have an algebraic singularity and as a result a

numerical solution cannot be initiated at this point. This diﬃculty is avoided

by obtaining an asymptotic solution. Instead of starting y = 0, it is necessary

to start at y = ∂ywhere∂y << 1 as follows.

α+β

(w + k)

−α/π

(w − ℓ)

−β/π

(w −1)

−1

(9.108)

w=0

α+β

(k)

−α/π

(ℓ)

−β/π

(−1)

−1

. (9.109)

Therefore

z=−A

(k)

−α/π

(−ℓ)

−β/π

(

α+β

)



α+β



(9.110)

= −A

(k)

−α/π

(ℓ)

−β/π

(u + iv)

(

α+β

)



α+β



. (9.111)

Hence

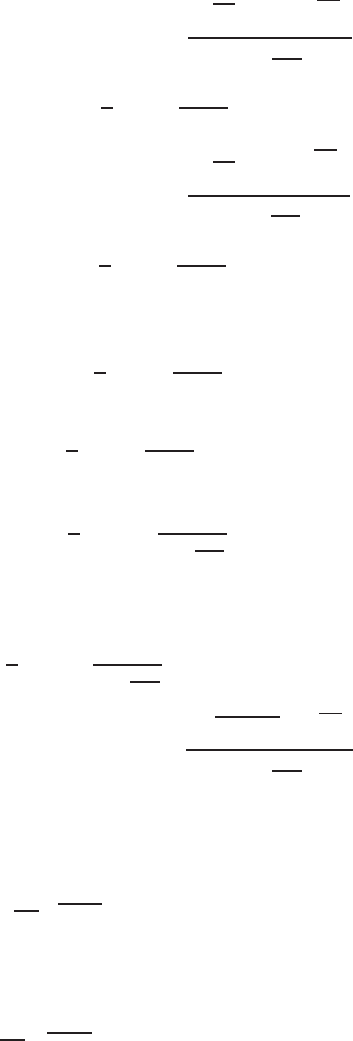
288 9 Complex Variables and Conformal Transformation in Poten tial Theory

x=− A

. (k)

−α/π

(ℓ)

−β/π



√



(

α+β

)



α+β



(9.112)

cos



tan

−1



α + β



− β



y=− A

. (k)

−α/π

(ℓ)

−β/π



√



(

α+β

)



α+β



(9.113)

sin



tan

−1



α + β



− β



Since x = 0 through out the path

cos



tan

−1



α + β



− β



= 0 (9.114)



tan

−1



α + β



− β



= π/2.

Hence

=tan



π/2+β

α+β



. (9.115)

Either v or u may be chosen arbitrarily such that it is very nearly equal to

zero. Then

tan



π/2+β

α+β



. (9.116)

= −A

. (k)

−α/π

(ℓ)

−β/π







(

α+β

)



α+β



. (9.117)

It is now p ossible to integrate the (9.116) and (9.117) numerically. The pro-

jection of the epicentre is given by

= −



Im ag



−(α+β)

(w + k)

α/π

(w − ℓ)

β/π

(w −1)



dy. (9.118)

and

0=−



Real



−(α+β)

(w + k)

α/π

(w − ℓ)

β/π

(w −1)



dy. (9.119)