Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

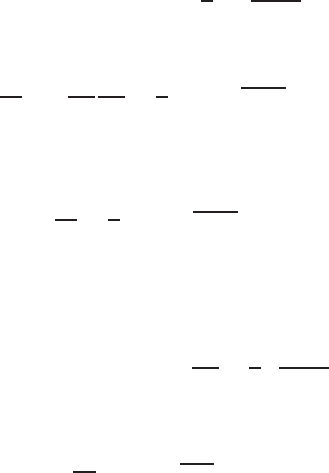
9.6 Geophysical Problems on S-C Transformation 289

In principle, (9.118) and (9.119) can now b e used to solve for ‘k’ and ‘l’

uniquely. For solution of the problem values of ‘k’ and ‘l’ satisfying (9.118)

and (9.119) are selected and ‘h’, for which (9.104) is satisﬁed, is determined.

By varying ‘k’ ‘l’ , ‘h’ can be varied; however, this method is not particularly

convenient if it is desired to vary h in regular steps. It may be n oted that

(9.118) and (9.119) are non-linear and can be solved only numerically. The

Runge-Kutta method of order four was used. Figure 9.11c shows the trajectory

of the path in the W-plane as the point moves from A (Fig. 9.11a) to the

epicentre of the point A on the surface. It is needed for point to point mapping.

Computation of Telluric Field and Apparent Resistivity

Having transformed the complex geometry of the problem into a simple one,

the ﬁeld problem in the w-plane is solved ﬁrst and then it is transferred

onto the z-plane. The telluric ﬁeld in the z-plane may be looked upon as

that due to a point source and a point sink placed at ±∞ respectively. After

transformation the point source at +∞ is mapped onto DD

′

while the sink is

still at inﬁnity. The boundary conditions in the w-plane are: Potential gradient

across the real axis is zero and the pot ential goes to zero on the semicircle

with inﬁnite radius in the upper half of the w-plane. The potential due to

a po int sour ce, satisfying the above boundary conditions and the Laplace’s

equation is

φ =



w − 1

. (9.120)

The gradient is transferred to the z-plane and the ﬁeld equation is

E=−

dφ

= −

dφ

−1

(w)

−(α+β)

(w + k)

α/π

(w − ℓ)

β/π

. (9.121)

Since the telluric ﬁeld is measured on the earth’s surface (where y = 0 and

v = 0), (9.121) may further be simpliﬁed to

E=−

dφ

−1

(u)

−(α+β)

(u + k)

α/π

(u − ℓ)

β/π

. (9.122)

To determine the telluric ﬁeld at a given point on the x-axis, the map of x on

the u axis is computed and then (9.122) is evaluated taking point by p oint

mapping. From (9.120) we can write the telluric ﬁeld as

E=−

dφ



w − 1

. (9.123)

The (9.105) changes to

(u)

−α+β

α/π

(u − ℓ)

β/π

(u − 1)

−1

(9.124)

for the purpose of mapping on the real axis. Taking its inverse the equation is

290 9 Complex Variables and Conformal Transformation in Poten tial Theory

−1

(u)

−(α+β)

(u + k)

α/π

(u − ℓ)

β/π

(u − 1)

−1

(9.125)

which may be considered as a non-linear diﬀerential equation connecting u and

x. By integrating (9.118) and (9.119) numerically with the initial condition,

viz. u = u

at x = 0 which was determined earlier, a map of any p oint on the

real x-axis is obtained. Figure 9.10d shows the telluric ﬁeld response over an

anticlinal structure.

9.6.4 Problem 4 Telluric Field Over a Faulted Basement (Horst)

In this section a problem is pr esented where closed form solution is obtained

and conformal transformation is used along with elliptic integrals and elliptic

functions. For the beneﬁt of the readers a brief outline of the elliptic integrals

and elliptic functions are given in Sect. 9.7. (Roy 1973).

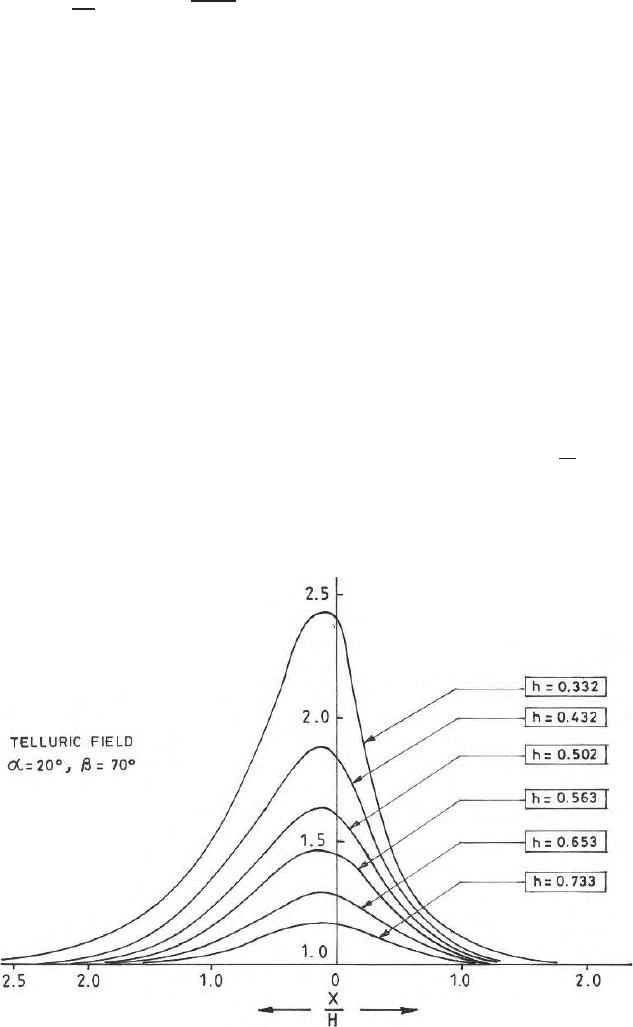
A two dimensional model of the horst is shown in (Fig. 9.12 a, b). In this

section a rectangular basement structure is chosen. As in the previous case

it is assumed tha t the resistivity ‘ρ’ and the thickness ‘H’ of the sedimentary

layer are both unity. ‘h’ and ‘d’ are respectively the throw of the fault and

half width of the horst. In the z-plane the source and sink are assumed to

be at ±∞ so that in the w-plane they are mapped at DE (w =

)andat

′

(w = −1/k

) respectively.

Since the basement is assumed to be of inﬁnite resistivity, the problem

reduces to a Neumann problem, i.e., th e potential should satisfy Laplace’s

(d)

Fig. 9.11. (d)Telluric ﬁeld anomaly over an asymmetric anticline

9.6 Geophysical Problems on S-C Transformation 291

Fig. 9.12 a, b. Show the faulted basement with h orst type of structure in the Z-

plane and its map on the real axis of the W-plane; map of surface and subsurface

onto the real axis of the w-plane ; ﬂow of direct current from inﬁnity; long line source

and sink placed at inﬁnite distance away in the z-plane and are respectively mapped

at DE and E’D’ on the real axis

equation with the condition that the normal gradient

∂φ

∂n

= 0 throughout the

entire boundary FEDCBA B

′

. A two dimensional potential distribu-

tion in a homogeneous isotropic and in a source free region is given by the

Laplace’s equation.

Closed form mathematical solution can be obtained using conformal trans-

formation and elliptic integrals and functio n. These problems satisfy Laplace

equation

∂

φ (x, y)

∂x

∂

φ (x, y)

∂y

=0. (9.126)

292 9 Complex Variables and Conformal Transformation in Poten tial Theory

Using the method of Schwarz – Christoﬀel transformation. The transformation

function for the present problem may be expressed in the diﬀerential form as

=A (w −1)

1/2

(w − a)

−1/2

(w −b)

−1

(w + 1)

1/2

(w + a)

−1/2

(w + b)

−1



− 1



1/2

− a

)

1/2

− b

)

(9.127)

z =A





− 1



1/2

− a

)

1/2

− b

)

+ C

. (9.128)

Here C

= 0, b ecause the origin in the z-plane is ﬁxed. Equation (9.128)

is in the form of an elliptic integral. The above integral is brought into a

standard form by substituting a = 1/kandb=1/k

(Kober 1957) and

Byrd Friedman (1954). In the next section, an introductory level discussion

on elliptic integrals and elliptic functions are given. For better background,

the readers will have to read the standard text books on elliptic integrals and

functions. Equation (9.128) therefore reduces to

z=C





1 −w



1/2

(1 −k

)

1/2

(1 −k

)

(9.129)

where C = −k

is a new constant. Hence the values of C, k and k

are to

be known before solving the boundary value problem. In order to evaluate

the constant C the following boundary condition is applied. It is noted from

(9.129) that at the p oint w = 1/k

an algebraic singularity is present. There-

fore, (9.129) is integrated around an inﬁnitesimal semicircle from w =

+ ε

to w =

− ε where ε → 0 and thus the singular point is avoided. However,

the approach is diﬀerent from that shown in the previous problem. Since the

shift in the z-plane is ‘iH’ the (9.129) can be written as :

iH = C



1 −1/k



1/2

(1 − k

)

1/2

(1 + k

⎧

⎨

⎩



(1 −k

⎫

⎬

⎭

1/k

+ε

1/K

−ε



1 −1/k



1/2

(1 − k

)

1/2

(1 + k



−

log (k

w − 1)



1/k

+ε

1/K

−ε

. (9.130)

Now as w passes through the singular point (w = 1/k

), the expression (k

w− 1)

changes its sign, i. e., log (k

w − 1) increases by an amount −iπ. Therefore, the

change in the value of −





log (k

w −1) from

− ε to

+ ε is i

Hence

iH =



1 −k



1/2

2(k

− k

)

1/2

9.6 Geophysical Problems on S-C Transformation 293

And



− k



(1 + k

)

1/2

. (9.131)

Substituting k

=ksnα one gets



− k



1/2

(1 −k

α)

1/2

ksnα

snα cnα

dnα

. (9.132)

where snα,cnα and dnα are the Jacobian elliptic functions. In order to eval-

uate the constants k and k

(or k and α since k

=ksnα), it is necessary to

integrate (9.129) and then to apply suitable boundary conditions.

Equation (9.129) can be r ewritten in the form

z=C





1 −w



(1 −k

)

1/2

(1 −k

)(1− w

)

1/2

. (9.133)

The form of the integral suggests that it is an elliptic integral of the third

kind which can be separated into two parts:



(1 −k

)

1/2

(1 −k

)(1− w

)

1/2

(9.134)

and



(1 −k

)

1/2

(1 −k

)(1− w

)

1/2

(9.135)

Here I

=Cπ (w, k, k

), i.e. the standard Legendre’s from of elliptic integrals

of the third kind. However, it is diﬃcult to express I

in the Legendre’s form.

In order to avoid this diﬃculty both the integrals are transformed into the

Jacobian form by substituting

w=snλ

therefore

dw = cn λ dn λ dλ.

Since

dn λ =(1− k

λ)

1/2

and

cn λ =(1− sn

λ)

1/2

294 9 Complex Variables and Conformal Transformation in Poten tial Theory

The integral I

can b e rewritten as





1 −k



1/2



1 −sn



1/2

dλ

(1 − k

λ)

1/2

(1 −k

λ)

1/2

(1 − sn

λ)

1/2

(9.136)



dλ

(1 −k

λ)

⎧

⎨

⎩

λ +k



λdλ

(1 − k

λ)

⎫

⎬

⎭

where k

=ksnα



λ +

sn α

cnα dnα

π (λ, α)



(9.137)

where π(λ, α) is the Jacobian form of the el liptic integral of the third kind.







1 −sn



1/2



1 −k



1/2

dλ

(1 −k

λ)

1/2

(1 −k

λ)

1/2

(1 −sn

λ)



λdλ

(1 −k

λ)

π (λ, α)

snα cnα dnα

. (9.138)

Hence

z=C



λ +

snα

cnα dnα

π (λ, α) −

π (λ, α)

snα cnα dnα



. (9.139)

Equation (9.139) is the function required for mapping the z-plane onto the

real axis of the w-plane.

Now at w = 1/k, z=d− ih as shown in Fig. 11 b, c. Therefore

λ =sn

−1

1/k



(1 −w

)

1/2

(1 −k

)

1/2

=K+iK

′

. (9.140)

Here K and K

′

are the complete elliptic integrals of the ﬁrst kind from the

deﬁnition. Hence (9.139) can be rewritten as

d−ih = C





K+iK

′



snα

cnα dnα



K+iK

′

, α



−



K+iK

′

, α



snα cnα dnα

. (9.141)

From the well-known relation between the Jacobi’s elliptic integral of the third

kind and his theta and zeta functions one can write

9.6 Geophysical Problems on S-C Transformation 295



K+ik

′

, α



log



K+ik

′

− α





K+iK

′

+ α





K+iK

′



Z(α) (9.142)

which simpliﬁes to

KZ (α)+i



πα

+ K

′

Z (α)



(9.143)

where z (α) is the Jacobi’s zeta function. On substituting the value of C and

π(K + iK

′

, α) (9.139) b ecomes

d −ih =

cnα snα

dnα





K+iK

′



snα

cnα dnα



(9.144)



KZ(α)+i



πα

′

Z(α)



−

snα cnα dnα



KZ(α)+i



πα

′

Z(α)



. (9.145)

Separating the real and imaginary parts one gets the following two equations

π dnα



cnαsnα +

dnα

Z(α) −

Z(α)

dnα

(9.146)

πdnα



dnα



πα

′

Z(α)



−

dnα



πα

′

Z(α)



− K

′

cnα snα

(9.147)

Mention may b e made that all the factors, e.g., K, K

′

,snα,cnα,dnα,Z(α)

are dependent on the values of k and α. Only two equations are available and

there are several unknowns. It is not possible as yet to determine the values

of k. and k

(or k snα) from known values of d/H and h/H which are ﬁxed by

the geometry of the structure. To avoid this diﬃculty the process is reversed.

In that, a series of values of k and α are assumed and the corresponding values

of d/H and h/H are determined. The values of k and α canbeestablishedfor

a given set of d/H and h/H ratios. For chosen values of k and α,thevalueof

C can b e determined as

snα cnα

dnα

. (9.148)

Mapping the desired region onto the upper half of the w-plane along the entire

u-axis, the problems can now be solved. In order to plot the telluric ﬁeld

point by point on the surface, the values of u for diﬀerent values of x must

be known. For this purpose, the inverse transformation function (indicated in

the previous problem), from (9.127) can be written as:



1 −k



1/2



1 −k



(1 −w

)

1/2

. (9.149)

Since

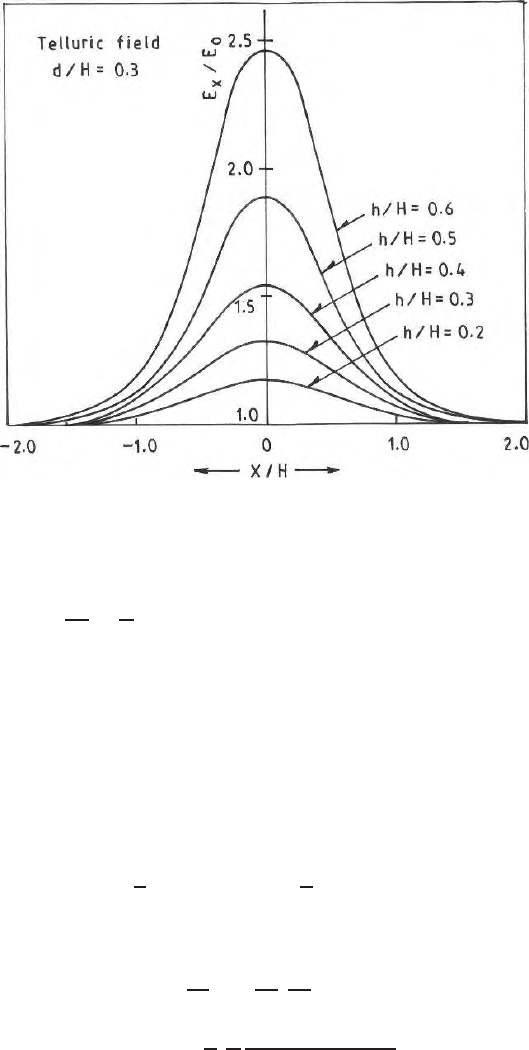
296 9 Complex Variables and Conformal Transformation in Poten tial Theory

Fig. 9.13. Telluric ﬁeld anomaly over a horst type of structure

the (9.149) reduces to



1 −k



1/2



1 −k



1 −u



−1/2

(9.150)

because v = 0 on the u-axis which corresponds to the air earth boundary in

the z-plane (for ∞ > u > 1/k

Equation (9.150) is a non-linear diﬀerential equation and, in principle,

may be numerically integrated. Although it is necessary to know the values

of both ‘u’ and ‘x’ at the staring point, in order to determine the telluric ﬁeld

as explained earlier, the source and the sink is placed at ±∞ in the z-plane

such that they are at w = 1/k

and w = −1/k

respectively in the w-plane.

The potential distribution is given by

φ = −

log (w − 1/k

log (w + 1/k

) . (9.151)

Therefore, the telluric ﬁeld on the surface (Fig. 9.13) is given by

E=−

dφ

= −

dφ

= −



1 −k



1/2

(1 − u

)

1/2

. (9.152)

9.7 Elliptic Integrals and Elliptic Functions 297

In this section one problem is presented where conformal transformation is

used along with the elliptic integrals and elliptic functions. Researchers on

electrical communication, electrical power engineering and applied mathemat-

ics need thi s kind of solution of boundary value pro b lems.

Analytical solution results can be compared with those obtained numeri-

cally for calibration of the ﬁnite element or ﬁnite diﬀerence code.

9.7 Elliptic Integrals and Elliptic Functions

Let us consider the integral

λ =



(1 −w

)

1/2

(1 −k

)

1/2

. (9.153)

The constant k is called the modulus of λ. In actual physical problems the

value of k is found to vary in between zero and unity. For this reason k can

be, an d often is, designed by sin θ where θ is called the modulus angle. This

integral is called the elliptic integral of the ﬁrst kind. Such integ rals were called

elliptic because they were ﬁrst encountered in the determination of length of

arc of an ellipse. The form of the integral (9.153) is known as Jacobi’s notation

of the elliptic integral.

9.7.1 Legendre’s Equation

Second notation is that of Legendre. It can be obtained from that of Jacobi

by putting

w=sinφ (9.154)

where φ is called the amplitude angle. This angle may be obtained from θ the

modulus angle. We get

λ =



dφ



1 −k

sin



1/2

. (9.155)

The integral in (9.155) is the elliptic integral o f the ﬁrst kind. In Legendre’s

notation φ =amα signifying that φ is the amplitude of α.

9.7.2 Complete Integrals

If the upper limit of the integral is made unity the integral is said to be

complete. The complete elliptic integral of the ﬁrst kind is always denoted by

K and hence

298 9 Complex Variables and Conformal Transformation in Poten tial Theory



(1 − w

)

1/2

(1 − k

)

1/2

. (9.156)

Equation (9.156) gives k in Jacobi’s notation. In Legendre’s notation since

w=sinφ, the limits of integration are from zero to π/2. Hence in Legendre’s

notation

π/2



dφ



1 −k

sin



1/2

. (9.157)

It may sometimes be necessary to state the modulus of K. We then write K

(k) for the c omplete elliptic integral of the ﬁrst k i n d of modulus k.

The Complementary Modulus

We now need to deﬁne a complementary modulus k

′

related to the modulus

k by the equation k

′2

=1or

′

=(1−k

)

1/2

(9.158)

From (9.158), when k is written as sin θ, k

′

must be written as cos θ.

The complete elliptic integral of the 1st kind to modulus k

′

must be entirely

diﬀerent from K which has the modulus k.

′

(k) = K(k

′

). (9.159)

Hence K a nd K

′

are related through their modulus and K, K

′

must be a real

number.

By this deﬁnition K

′

is given by the integral

′



(1 − w

)

1/2

(1 − k

′2

)

1/2

. (9.160)

The next thing to ﬁnd is the equation deﬁning K

′

in terms of the normal

modulus k. In (9.160), let

(1 −k

′2

)

1/2

′2



1 −



− 1

′2

(9.161)

Therefore,