Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

10.3 Corollaries of Green’s Theorem 309

10.3 Corollaries of Green’s Theorem

Some of the Corollaries of Green’s theorem are as follows:

Cor. 1 If φ and ψ are both harmonic and continuous within the region R,

then





∂ψ

∂n

− ψ

∂φ

∂n



ds = 0 (10.9)

since both ∇

φ = ∇

ψ =0andφ and ψ satisfy Laplace equation.

Cor. 2 If φ is harmonic and continuously diﬀerentiable in a closed region then

the integral of the normal derivative of φ over the boundary vanishes.

If we put ψ =1, then



∂φ

∂n

ds = 0. (10.10)

This region do es not include any source. The surface integral of the normal

derivative of a harmonic function over any closed surface is zero.

Cor. 3 If a function φ is harmonic in a closed sphere of radius ‘a’ with the

centre at the point C, then φ

is equal to the average of its values on the

boundary surface. This is known as the mean value theorem or the average

value theorem in potential theory. If this theorem is applied in the case of

bodies of simpler geometrics, say, in the case of a sphere (Fig. 10.2) then for

a sphere, the normal is along the radial direction,

∂φ

∂n

∂φ

∂r

.Elementaryarea

ds = r

sin θ dθ dψ,whereθ and ψ are respectively the polar and azimuthal

angles.

Hence



∂φ

∂n

ds =



∂φ

∂n

sin θ dθ dψ

2π



∂φ

∂r

sin θ dθ dψ = 0 (10.11)

Fig. 10.2. A sphere of outer and inner radii ‘a’ and ‘r’ respectively

310 10 Green’s Theorem in Potential Theory

Multiplying both the sides of (10.11) by dr and integrating with in the region,

we get



2π



∂φ

∂r

sin θ dθ dψ =0

⇒

2π



(φ

− φ

sin θ dθ dψ =0

⇒

2π



sin θ dθ dψ − 4πr

φ (c) = 0

⇒ φ

4πr

2π



sin θ dθ dφ

4πr

2π



4πr



ds. (10.12)

This gives the value of the potential at the centre which is the average of its

potential on the surface i.e., the mean value theorem is



ds (10.13)

Cor. 4 If a function φ is harmonic in a closed sphere, then φ

at the centre

is equal to the average of its value through out the sphere. This is the second

average value or mean value theorem.

From (10.12), we can write



4πr

dr =



φ dsdr =



φ dν (10.14)

where a is the radius of the sphere. Therefore

⇒ φ



φ dν. (10.15)

Here the sphere considered is a solid sphere and ν is the volume of the sphere.

Cor. 5 If φ is a harmonic function and not constant in a closed region, then

φ cannot have maximum or minimum inside the regio n.

10.4 Regular Function 311

Cor. 6 A maximum or a minimum value of a harmonic function occurs only

at a boundary of the region.

Cor. 7 If a function is harmonic in a region and is constants on the surface,

then it is constant throughout the region.

Cor. 8 Two functions φ and ψ which are harmonic in a region and are equal

at every point in the boundary are equal at every point in the region.

Cor. 9 If a solution of Laplace equation is found and has prescribed values

on the boundary, then the solution is un iq u e. This is known as the uniqueness

theorem in potential theory.

Cor. 10 If a function is harmonic in a closed region and its normal derivatives

vanish in the boundary, then the function is constant throughout the region.

Cor. 11 If two functions are harmonic in a closed region and have the same

normal derivative at the boundary, then they diﬀer by a constant.

10.4 Regular Function

The space outside the closed volume (Fig. 10.1) is called the inﬁnite region

where r →∞. If there be any function φ such that Lim

r→∞

rφ = ﬁnite or

Lim

r→∞

rgradφ = ﬁnite then φ is called a regular function at inﬁnity. A potential

function is a regular function provided the source do es not exist in the region.

Cor. 12 A function is harmonic in an inﬁnite region if it has continuous

second derivative, satisﬁes Lapla ce equation and is regular at inﬁni ty.

With this deﬁnition of the harmonic and regular function, the theorem,

which we get is valid for inﬁnite region. For an inﬁnite region, the value

of a harmonic function is uniquely determined by the values of the normal

derivatives at the boundary.

Cor. 13 If φ and ψ are harmonic functions within a closed surface S and ψ

has a single pole on S so that

ψ =

+ ρ

where ρ is harmonic, then

φ (x, y, z)=

4π





∂ψ

∂n

− φ

∂φ

∂n

ds. (10.16)

Cor. 14 If φ and ψ are harmonic within a closed surface and φ and ψ have

single poles at ρ

and ρ

respectively and

φ =

+ ρ

and ψ =

+ ρ

312 10 Green’s Theorem in Potential Theory

then

4π





∂ψ

∂n

− ψ

∂φ

∂n



ds = φ (ρ

) −ψ (ρ

) (10.17)

where φ(ρ

) is the value of the function φ at the p oint ρ

10.5 Green’s Formul a

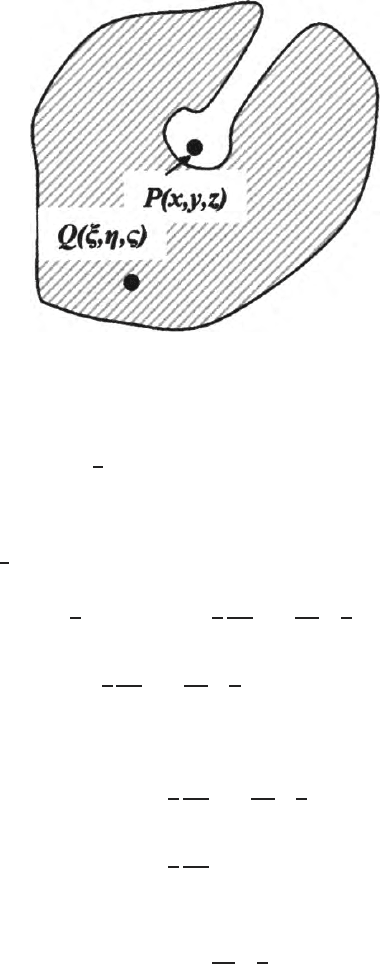
Let a ﬁnite region R is bounded by the surface S. The point Q may be within

the volume or outside the region. The point P also may be within or outside

the region (Fig. 10.3). The coordinates of P and Q are respectively (x, y, z)

and (ξ, η, ζ). Here P is the observation point. Then the value of

,which

behaves as a potential function, is given by



(x − ξ)

+(y− η)

+(z− ζ)



1/2

(10.18)

(a) When the point P is outside

Let us take

as a harmonic function and ψ as any other function. From

Green’s theorem, we get



∇

ψ dν =





dψ

∂n

− ψ

∂

∂n





ds. (10.19)

Fig. 10.3. Observation point P is outside the region R

10.5 Green’s Formula 313

Fig. 10.4. Observation point P is inside the region R

(b) When the point P is inside the body, ‘r’ may or may not be harmonic

strictly. We can isolate the point with a small semicircle (Fig. 10.4). In

the rest of the region

is harmonic. For this region, the normal is always

outside the region. The boundary, which demarcates the region, and the

boundary, which isolates the point P, should be taken into consideration

separately.

Using ∇





=0,weget



∇

ψ dν =





∂ψ

∂n

− ψ

∂

∂n







′



dψ

∂n

− ψ

∂

∂n





ds. (10.20)

Let





∂ψ

∂n

− ψ

∂

∂n







′



∂ψ

∂n

and



′



∂

∂n





ds.

Let us ﬁrst evaluate the second integral, which entered into the (10.20)

due to the origin of the second surface, which isolates the point P. The

circle which isolates the point P is of radius ‘a’. Therefore

314 10 Green’s Theorem in Potential Theory



′



−

∂ψ

∂r



sin θ dθ dψ. (10.21)

Here −

∂ψ

is the normal towards the centre because the movement is in

the clockwise direction as indicated by the arrows. Therefore

2π



−



∂ψ

∂r



sin θ dθ dψ. (10.22)

Now Lim

a→0

→ 0.

In the limit r → 0





−ψ

∂

∂n





ds. (10.23)

Since

∂

∂n





= −

when r → a, (10.23) reduces to

= −

2π



ψ sin θ dθ dψ. (10.24)

Now taking the limit a → 0, the integral reduces to 4πψ

when the point

P is inside. Green’s theorem changes to the form

= −

4π



∇

ψ dν +

4π





∂ψ

∂n

− ψ

∂

∂n





ds (10.25)

This is the expression for the potential at a point when the point P is

inside the region R.

When the point P is right over the boundary, the function

is not strictly har-

monic. Approaching in a similar way, we get the expressions for the p otentials

= −

2π



∇

ψ dν +

2π





∂ψ

∂n

− ψ

∂

∂n





ds (10.26)

because the solid angle subtended at the point P is 2π and not 4π.

If ψ is a potential function which is harmonic within the region then ∇

ψ =

0and

2π





∂ψ

∂n

− ψ

∂

∂n





ds. (10.27)

Now we can summarise the Green’s formulae for p otential as follows.

10.6 Some Special Cases in Green’s Formula 315

(a) When the point P is outside





∂ψ

∂n

− ψ

∂

∂n





ds =0. (10.28)

(b) When the point P is inside, then

4π





∂ψ

∂n

− ψ

∂

∂n





ds. (10.29)

This is the Green’s third formula.

2π





∂ψ

∂n

− ψ

∂

∂n





ds. (10.30)

Green’s ﬁrst and second identities are also known as Green’s formulae. The

second identity i.e., the Green’s symmetrical fo rmula is more frequently used.

Only the ﬁrst and second derivatives of φ and ψ enter in the surface integrals

and they are the normal derivatives. φ and ψ have continuous second deriva-

tives in the interior of the region V (entire volume). φ, ψ,

∂φ

∂n

and

∂ψ

∂n

remains

continuous in the closed reg i on v + s, i.e. volume plus surface.

The second derivatives of φ and ψ are piecewise continuous in the volume

V. Green’s theorem is valid for each of the subregions into which the V is

divided by the surface of discontinuity. By addition of these formulae for each

subregions, we can obtain the theorem for the entire region.

10.6 Some Special Cases in Green’s Formula

(a) when ψ =1,then





∇

φ dν =



∂φ

∂n

ds (10.31)

(b) if φ = ψ,then





(∇φ)

dν =



∂φ

∂n

ds −





φ∇

φdν (10.32)

φ =0,andonegets





(∇φ)

dν =



∂φ

∂n

ds. (10.33)

(d) If φ and ψ are b oth harmonic functions inside the closed surface S, then





∂ψ

∂n

− ψ

∂φ

∂n



ds = 0. (10.34)

316 10 Green’s Theorem in Potential Theory

10.7 Poisson’s Equation from Green’s Theorem

Let φ(ξ, η, ζ) is a function at a coordinate ξ, η, ζ which is continuous in a vol-

ume and is bound ed by a closed surface S. Its ﬁrst derivative is also continuous.

From Green’s theorem, we can write



∇

φ dν =



∂φ

∂n

ds (10.35)

for continuous and ﬁnite distribution of matters. Here φ is a potential function

for continuous and ﬁnite distribution of matters. From Gauss’s theorem, we

can write



∂φ

∂n

ds = −4π Mor



∇

φ dν = −4π M. (10.36)

Here M stands for the distribution of mass and is equal to M =



σdν.

σ(ξ, η, ζ) is the density of the matters distributed in the volume We can rewrite

(10.36) in the form





∇

φ +4πσ



dν = 0 (10.37)

It reduces to

∇

φ = −4πσ (10.38)

This is the Poisson equation and it is valid for any kind of distribution of

matters.

10.8 Gauss’s Theorem of Total Normal Induction

in Gravity Field

Let φ be the gravitational potential due to certain distribution of masses both

inside and outside the domain R. Let ψ, the other scalar potential function is

assumed to be constant both outside and inside the region S. We can write

from Green’s second identity



∇

φ dv =



∂φ

∂n

ds (10.39)

where φ is a harmonic function. Si nce ψ is assumed to be constant, its deriva-

tive with respect to the direction normal to the surface is zero. Let φ

and φ

out

are respectively the potential both inside and outside S. φ

out

obeys Laplace

equation is a source free region and φ

obeys Poisson’s equation because the

masses are included within the domain.





∇

out

dv = 0 (10.40)

10.9 Estimation of Mass in Gravity Field 317

and





∇

out

dv = −4πGM (10.41)

Here M is the total mass included by the surface. It is important to note these

Green’s formulae is independent of the sizes and shapes of the distribution of

masses and sizes and shapes of the boundaries. Hence





∇

φdv =



∂φ

∂n

ds = −4πGM (10.42)

This is Gauss’ law of total normal induction. It states that the total normal

gravitation ﬂux on a closed bounded surface is equal to 4πG times the total

M of one body or multiple bodies inside the closed domain. Here G is the

universal gravitational constant.

10.9 Estimation of Mass in Gravity Field

Since Gauss’ law of total normal induction is valid in gravity ﬁeld also, we

can assume that the anomalous masses which are generating gravity anomaly

because of density contrast are relatively nearer to the surface and we estimate

the total normal induction on the surface of a sphere of inﬁnite radius. We

divide this sphere into two hemispheres and the central horizontal plane which

cuts the sphere into two parts.The ﬁrst part represent the surface of the

earth, where we seek the mass to be est imated. And the second part is upper

hemisphere of inﬁnite radius.We can now write the total normal induction as



Plane

∂φ

∂n

ds +



Hemisphere

∂φ

∂n

ds = −4πGM (10.43)

We can divide the total normal induction equally in upper and lower hemi-

sphere and each sector will have −2πGM where M is the total anomalous mass.

This induction i s independent of the total number of bodies present and their

sizes and shapes. Therefore, on the surface, we can write the expression for

the integral on gravity anomaly as



surface

∆gds =2πGM (10.44)

where ∆g is the gravity anomaly and M is the mass excess due to density

contrast with the host rock. Surface integration is carried over the plane of

observation.

318 10 Green’s Theorem in Potential Theory

10.10 Green’s Theorem for Analytical Continuation

By analytical continuation we mean potential measured in o ne plane or level

can b e transferred to another plane or level mathematically or analytically

(see Chap. 16). If P is any point outside the domain with surface S and

where r is the distance of P from any volume element dv at Q inside

the domain bounded by S (Fig. 10.4). Since φ

is an harmonic function, it

satisﬁes Laplace equation ∇

= 0 at all points throughout V. Inside the

volume V

the potential satisﬁes Poisson’s equation. Therefore we can write

∇

φ = −4πGM, where G is the universal gravitational constant and M is

the total mass. From Green’s second identity or symmetrical form of Green’s

theorem, we can write

4π





Gρ dv





∂

∂n





−

∂φ

∂n

ds (10.45)

⇒ φ

4π





∂





−



∂φ

∂n



ds (10.46)

where



Gdm

(10.47)

is the potential at P due to mass distribution inside S. One can estimate the

potential at any point outside a closed surface S if the potential φ and its

normal derivative

∂φ

∂n

are known at all points on the surface. The potential

φ is the combined potential due to the masses inside and outside S. φ is the

potential due to the masses enclosed by the surface only.

Now on the surface of a hemisphere

∂

∂n





=0and(1/r)



∂φ

∂n



because the hemisphere rad iu s is inﬁnitely high. Hence (10.47) becomes

4π



Plane



∂

∂n





−

∂φ

∂n

(10.48)

Figure 10.5 shows that the images of mass distribution are within the enclosed

volume of the upper hemisphere. These images also produce the potential on

the boundary surface of the two hemisphere. If φ

is the potential due to the

distribution of images in the upper hemisphere, the potential and its normal

derivatives must be equal on the plane which divides the two hemispheres.

Since the normals n and n

are in the opposite direction, we can write