Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.

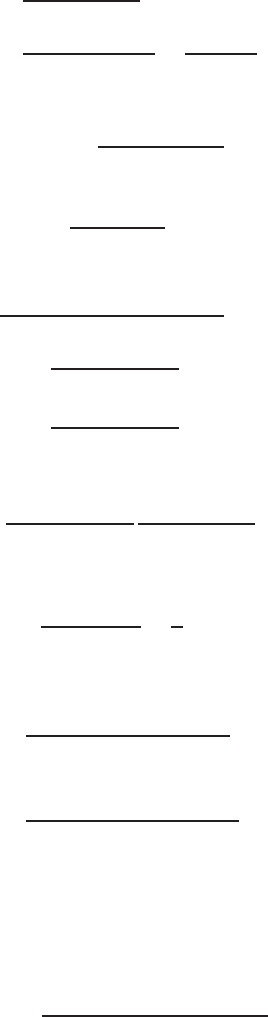
9.7 Elliptic Integrals and Elliptic Functions 299
1 −w
2
=
k
′2
t
2
− t
2
+1
k
′2
t
2
=
1 −t
2
1 −k
′2
k
′2
t
2
=
1 −k
2
t
2
k
′2
t
2
and hence
1 −w
2
1/2
=
1 −k
2
′
t
2
1/2
k
′
t
(9.162)
Furthermore from (9.161)
w=
t
2
− 1
1/2
k
′
t
Therefore
dw =
t
2
t
2
− 1
−1/2
t
2
− 1
1/2
k
′
t
2
dt (9.163)
⇒
t
2
−
t
2
− 1
k
′
t
2
(t
2
− 1)
1/2
⇒
dt
k
′
t
2
(t
2
− 1)
1/2
.
Substituting these values, we get
k
′
=
dt
k
′
t
2
(t
2
− 1)
1/2
k
′
t
(1 −k
′2
t
2
)
1/2
with new limits. To find the new limits note that when w = 0, t=1andwhen
w=1
t=
1
(1 −k
′2
)
1/2
=
1
k
.
Therefore, simplifying the integrand and adding the new limits, we get
k
′
=
1/k
1
dt
(t
2
− 1)
/2
(1 −k
′2
t
2
)
1/2
k
′
=
1/k
1
dt
i(1− t
2
)
/2
(1 −k
′2
t
2
)
1/2
(9.164)
and this is the required relation. Notice that the integral is the same as that
for k but the limits are changed and the integral is imaginary. Combining the
integrands of K and K
′
one gets the total int e gration from the lower limit zero
to the upper limit 1/k and it is the complex number
K+iK
′
=
1/k
1
dw
(1 − w
2
)
1/2
(1 −k
′2
w
2
)
1/2
. (9.165)

300 9 Complex Variables and Conformal Transformation in Poten tial Theory
9.7.3 Elliptic Functions
The elliptic functions of interest to eng in eers are Jacobi’s elliptic functions.
λ =
ω
0
dw
(1 −w
2
)
1/2
=sin
−1
w. (9.166)
Thus the effect of getting rid of k is to make λ a function only of w and more
over an elementary function of w. we get
w=sinλ.
It can b e shown that Legendre’s form of the integral can be obtained by
putting
w=sinφ
=sin amλ
=snλ
=snλ (k)
=sn(λ, 0) = sin λ. (9.167)
Now
(1 − w
2
)
1/2
=cosφ = cos am λ
=cnλ =cn(λ, k). (9.168)
Since sin
2
φ +cos
2
φ = 1, it can be deduced that
sn
2
λ +cn
2
λ = 1 (9.169)
dn λ =(1−k
2
w
2
)
1/2
=(1−k
2
sin
2
φ)
1/2
=(1−k
2
sn
2
λ)
1/2
. (9.170)
The three functions snλ,cnλ,dnλ are the principal Jacobian elliptic functions
tn λ =
sn λ
cn λ
. (9.171)
We have defined
K=
π/2
0
dφ
1 −k
2
sin
2
φ
1/2
.
If the upper limit of the integral is some value of φ less tha n π/
2
, the integral
is incomplete and is then written as F (φ, k). Thus
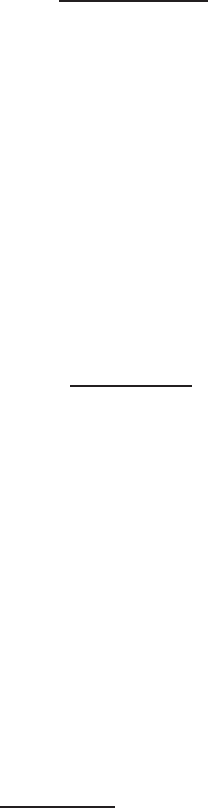
9.7 Elliptic Integrals and Elliptic Functions 301
F(φ, k) =
φ
0
dφ
1 −k
2
sin
2
φ
1/2
. (9.172)
The integral is frequently written in terms of the amplitude angle and the
modular angle as F (φ, θ) and rather less frequently in terms of the amplitude
and modulus as F (w, k). Here
F(w, k) = F(π/2, k) ≡ K(k) = K (9.173)
F(w, k) = F(φ, k) = λ (9.174)
We have
λ =sn
−1
(w, k) (9.175)
Therefore
sn
−1
(w, k) = F(w, k)
I=
w
0
1 −k
2
w
2
1/2
(1 − w
2
)
1/2
dw. (9.176)
This is the Jacobi’s form of the elliptic integral of the second kind and it is
denoted by E (w, k) where, as before, w is the argument or amplitude and k
is the modulus. Legendre’s form is given by
E(φ, k) =
φ
0
1 −k
2
sin
2
φ
dφ (9.177)
Another form is obtained by introducing the variable u where φ is the
amplitude of u.
sin φ =snu
and by differentiating both sides
cnφ dφ = cnu dnu du.
dφ =
cnu dnu du
(1 −sn
2
u)
1/2
=dnudu. (9.178)
The integral (9.177) can b e written as
E(u, k) =
u
0
1 −k
2
sn
2
u
1/2
dnu du
=
u
0
dn
2
udu. (9.179)

302 9 Complex Variables and Conformal Transformation in Poten tial Theory
It defines the elliptic integral of the second kind in terms of elliptic functions.
Complete elliptic integrals of th e second kind is expressed as
E(1, k) ≡ E(π/2, k) ≡ E(k) ≡ E (9.180)
9.7.4 Jacobi’s Zeta Function
Z(φ)=E(φ)=Z(φ)
E
K
(9.181)
all to modulus k.
9.7.5 Jacobi’s Theta Function
More important still are Jacobi’s Theta functions. His original theta function
is denoted by Θ and widely used an d they are indeed almost indispensable.
Z(φ)=
Θ
′
(φ)
Θ(φ)
a relation given by
φ
0
Z(φ)dφ =logΘ(φ) + C (9.182)
where series for theta function is
Θ(φ)=1+2
∞
m=1
(−1)
m
.q
m
2
cos
mπφ
k
(9.183)
where q = e
−π
K
′
K
.
Elliptic Integral of the Third kind is
π (w, k
1
, k) =
w
0
dφ
(1 −k
2
1
w
2
)(1− k
2
w
2
)
1/2
(1 −w
2
)
1/2
. (9.184)
Now putting w = sin φ giving
π (φ, k
1
, k) =
φ
0
dφ
1 −k
2
1
sin
2
φ
1 −k
2
sin
2
φ
1/2
. (9.185)
If we put w = snu
dw = cnu dnu du
π (u, k
1
, k) =
u
0
du
1 −k
2
1
sn
2
n
. (9.186)
All these are three forms of Legendre’s elliptic integral .
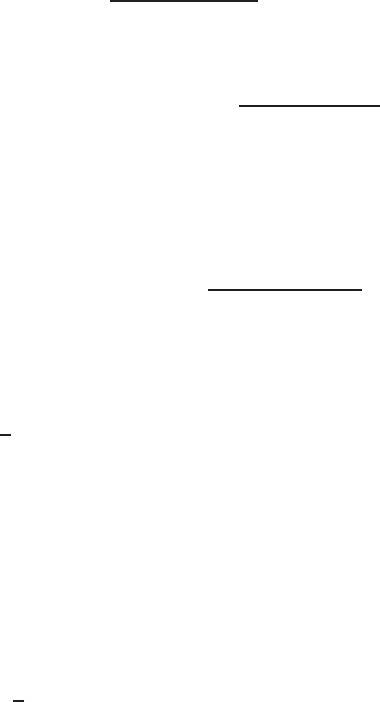
9.7 Elliptic Integrals and Elliptic Functions 303
9.7.6 Jacobi’s Elliptic Integral of the Third Kind
Jacobi adopted not merely a different form but an entirely different way of
presentation of elliptic integrals of the third kind.
Putting
k
1
=ksnα to mod k,
the integrand is
=
du
1 −k
2
sn
2
α sn
2
u
. (9.187)
With this substitution Jacobi defined his elliptic integral of the third kind as
π (u, α)=k
2
snα cn α dn α
u
0
sn
2
udu
1 −k
2
sn
2
α sn
2
u
(9.188)
(H.E.I.E.P. Handbook of Elliptic Integrals for Engineers and Physicists
400.01).
Jacobi’s definition of the elliptic integral can be expressed in terms of his
zeta function and also in terms of his theta functions
sn (u + α)+sn(u− α)=
2snucnα duα
1 −k
2
sn
2
usn
2
α
.
(H.E.I.E.P.123.02) (9.189)
And hence substituting these values
π (u, α)=
1
2
k
2
snα
u
0
snu {sn (u + α)+sn(u− α)} du. (9.190)
But from (H.E.I.E.P. 142.02)
k
2
snα snu sn(u + α)=−Z(u + α)+Z(u)+Z(α)
and
k
2
snα snu sn(u − α)=Z(u− α) − Z(u) + Z(α).
Hence
π (u, α)=
1
2
u
0
{Z(u− α) − Z(u+α)+2Z(α)} du. (9.191)
This gives a definition of Jacobi’s elliptic integral of the third kind in terms
of this zeta function.
Since
u
0
Z (u) du = log Θ (u) + C, (9.192)
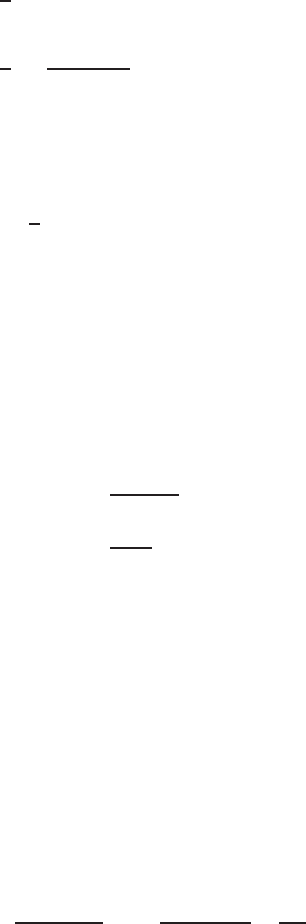
304 9 Complex Variables and Conformal Transformation in Poten tial Theory
we get
π (u, α)=
1
2
{log Θ (u −α) − log Θ (u + α)} +
u
0
Z(α)du
=
1
2
log
Θ(u− α)
Θ(u+α)
+uz(α) . (9.193)
It gives yet another definition of the elliptic integral of the third kind in terms
of his zeta and theta functions.
Real and Imaginary parts of π(K+iK
′
, α)
π
K+iK
′
, α
=
1
2
5
log Θ
K −α +iK
′
− log Θ
K+θ +iK
′
6
+
K+iK
′
Z(α) . (9.194)
From H.E.I.E.P. 141.01
Z(K − α +iK
′
) −Z(K −α)+cs(K− α) du(K − α) − iπ/2K. (9.195)
Integrating both sides of this equation with respect to (K−α), the integration
of the zeta functions can b e taken.
The integration of csu dnu can b e found as
cs u dn u du =
csu dnu
snu
du (H.E.J.E.P. 120.02)
=
dsnu
snu
=log snu. (9.196)
The complete integration therefore produces
log Θ(K −α +iK
′
)+C
1
=logΘ(K− α)+C
2
+log sn(K− α) − iπ(K − α)/2K. (9.197)
Similarly
log Θ(K + α +iK
′
)+C
1
=logΘ(K+α)+C
2
+log sn(K+α) −iπ(K + α)/2K. (9.198)
By subtraction
log Θ(K −α +iK
′
) −log Θ(K + α +iK
′
)
=log
Θ(K− α)
Θ(K+α)
+log
sn (K − α)
sn (K + α)
+
iπ
2K
(2α) . (9.199)
From H.E.I.E.P. 1051.03

9.7 Elliptic Integrals and Elliptic Functions 305
=log
Θ(K− α)
Θ(K+α)
+log
Θ
1
(−α)
Θ
1
(α)
=log1=0.
Similarly
=log
sn (K − α)
sn (K + α)
=log1=0.
Hence log Θ(K −α +iK
′
) −log Θ(K + α +iK
′
)=iπα/K.
And
π(K −iK
′
, α)=(K+iK
′
)Z(α)+iπα/2K. (9.200)
Necessary formulae for deriving the expressions ar e available in ‘Handbook of
elliptic integrals for engineers and physicists, by Byrd, P.F. and Friedman,
M.D. (1954) and ‘Elements of the theory of elliptic and associated func-
tions with applications by Dutta, M., Debnath, L. (1965). All the values of
snα, cnα, dnα, Z(α) are read from the ‘Jacobian elliptic function tables’ by
Milne-Thomson Dover New York (1950).

10
Green’s Theorem in P otential Theory
In this chapter Green’s first second and third identities are defined. Using
Green’s theorem one can arrive at Poisson’s equation. Gauss’ theorem of total
normal induction in gravity field, estimation of mass of a subsurface body
from gravitational potential are g iven. It could be shown that the basic for-
mula of analytical continuation of potential field can be derived from Green’s
theorem. Two dimensional nature of the Green’s identities are shown The-
ory of Green’s equivalent layer which explains the ambiguity in interpretation
of gravitational potentials is discussed. Application of Green’s theorem for
deriving Green’s function and analytical continuation are respectively given
in Chaps. 14 and 16. Nature of the vector Green’s theorem is shown.
10.1 Green’s First Identity
Let a region R includes the Vol. V en closed by the sur face S. Let φ (x, y, z)
and ψ (x, y, z) are two scalar functions and we assume that both ψ and φ are
continuous and have non-zero first and second derivatives(Fig. 10.1).
We can define a vector in the form
F=φ grad ψ (10.1)
Since
div
a
A
=adiv
A+
A grad a (10.2)
where a and
A are respectively a scalar and a vector. Applying divergence
operation on b oth the sides of (10.1), we get,
div
F = grad φ grad ψ + φ div grad ψ. (10.3)
Integrating both the sides, we get
ϑ
div
Fd ν =
ϑ
(grad φ grad ψ)dν +
ϑ
φ∇
2
ψdv. (10.4)
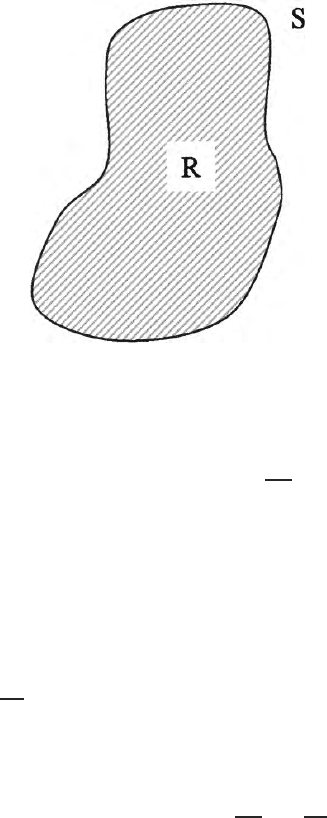
308 10 Green’s Theorem in Potential Theory
Fig. 10.1. A region R is having Vol. V and surrounded by the surface S
From Gausses divergence theorem , we get
ν
div
Fdν =
s
F
n
ds =
φ
∂ψ
∂n
ds. (10.5)
This is known as the Green’s Theorem in non-symmetrical form. It is also
known as the Green’s first identity.
If we write
F=ψ grad φ (10.6)
we get a complementary equation which can b e written in the form as
s
ψ
∂φ
∂n
ds =
ν
(grad ψ grad φ)dν +
ψ∇
2
φdv. (10.7)
Subtracting (10.7) from (10.5) , we get
ν
φ∇
2
ψ −ψ∇
2
φ
dν =
s
φ
∂ψ
∂n
− ψ
∂φ
∂n
ds (10.8)
This is known as the Green’s second identity or Green’s theorem in s ymmet-
rical form.
10.2 Harmonic Function
Harmonic function is defined as the function which is continuous within a
finite region R, it has non zero first and secon d derivatives and it satisfies
Laplace equation within the region.
