Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.


12.4 Mutual Inductance 359
Fig. 12.6. Mutual induction between the two coils carrying currents I
1
and I
2
Here emf in coil 2 is proportional to the rate of change of current in coil 1.
The constant of proportionality which is basically a geometric factor of the
two coils is termed as the mutual inductance and is written as
ε
2
=M
21
dI
1
dt
. (12.32)
If current I
2
passes through coil 2, then the emf in coil 1 will be
ε
1
=M
12
dI
2
dt
(12.33)
because field will be proportional to I
2
and the flux linkage through the coil
1wouldbe
dI
2
dt
.
12.4.1 Mutual Inductance Between any Two Arbitrary Coils
The general expression for the induced emf in the coil 1 is ε = −
∂
∂t
Bn.ds
where
B is the magnetic induction and the integral is taken over the surface
bounded by the coil 1. Applying Stoke’s theorem one can write
B.n.ds =
A.dl, where
A is a vector potential and
B=curl
A.dl
1
is the element of the
circuit in co il . The line integral is taken around the circuit 1. The emf in coil
1, can be written as
ε
1
= −
d
dt
A.dl
1
. (12.34)
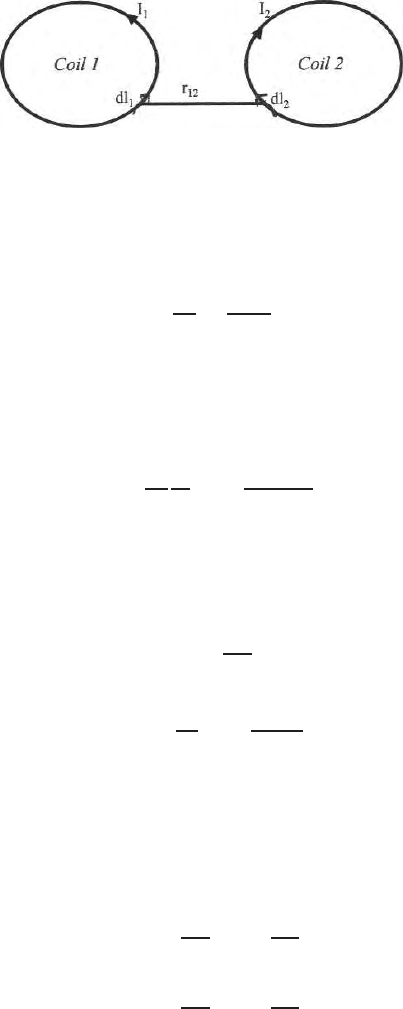
360 12 Electromagnetic Theory (Vector P otentials)
Fig. 12.7. Mutual inductance between the two noncoaxial arbitrary coils separated
by a certain distance
Let the vector po tential in circuit 1 comes from the current in circuit 2. The
line integral around the circuit 2 can be written as (Fig. 12.7)
A =
μ
4π
I
2
dl
2
r
12
(12.35)
where I
2
is the current in the circuit 2 and r
12
is the distance from the element
of the circuit dl
2
to the point of measurement on the circuit 1 at which we
are evaluating the vector potential. Hence the emf in the circuit 1 appears as
a double line integral.
ε
1
= −
μ
4π
l
dt
1
2
I
2
dl
2
dl
1
r
12
. (12.36)
In this equation, the integrals are all taken with respect to the stationary
circuits. The variable quantity I
2
does not depend upon the variable of inte-
gration. We can, therefore, write
ε
1
=m
12
dI
2
dt
. (12.37)
Here
m
12
= −
µ
4π
1
2
dl
1
dl
2
r
12
(12.38)
and m
12
is the mutual inductance.
If there are two currents in the two coils simultaneously, the magnetic flux
linking the two coils will be sum of the two fluxes linking separately. The emf
in either coil will therefore be proportional not only to the change of current
in the other coil but also to the change of current in the coil itself. Therefore,
the total emf is
ε
2
=m
21
dI
1
dt
+m
22
dI
2
dt
(12.39)
and
ε
1
=m
12
dI
2
dt
+m
11
dI
1
dt
(12.40)
The coefficients m
22
and m
11
are self inductances of the coils. The self induc-
tance exits for one coil. Here m
11
= −L
1
and m
22
= −L
2
where L
1
and L
2

12.4 Mutual Inductance 361
are the self inductances of the coil 1 and 2 respectively. Since emf generated
due to the rate of change of number of lines of forces oppose the changes of
current, according to Lenz’s law, the self inductances ar e negative.
12.4.2 Simple Mutual Inductance Model in Geophysics
Grant a nd West (1965) in a simple mu tual inductance model, demonstrated
the very basic nature of the electromagnetic resp onse one gets for geophysical
problems due to vertical magnetic dipoles used as a transmitter and a receiver.
Here conducting earth is repla ced by a vertical buried coil (Fig. 12.8)
Let us suppose that an alternating current I
o
e
iωt
is made to flow in the
transmitting coil. This current generates an alternating magnetic field in the
surrounding environment which in turn induces an emf both in the conductor
as well as in the receiving coil. These emf’s are governed by the Faraday’s law
of electromagnetic induction, i.e.,
E
j
= −M
ij
∂I
1
∂t
(12.41)
where E
j
is the emf induced in one circuit by the current I
1
flowing in another
circuit and M
ij
is the mutual inductance. The emf induced in the receiver by
the primary field is, therefore,
ε
2
= −M
02
d
dt
I
0
e
iωt
= −iωM
02
I
0
e
iωt
. (12.42)
Here M
02
is the mutual inductance between the transmitter and the receiver
coil. The emf induced in the vertical coil is
ε
1
= −iωM
01
I
0
e
iωt
(12.43)
where M
01
is the mutual inductance between the transmitting and the vertical
coil representing the subsurface. To this emf ε
1
, we must add ε
1
+
,thesumof
the voltage drop across the resistance and self inductance of the vertical coil
carrying current I
1
e
iωt
.Thus
Fig. 12.8. A simple mutual inductance model to represent electromagnetic Induc-
tion in the earth (Grant and West 1985)
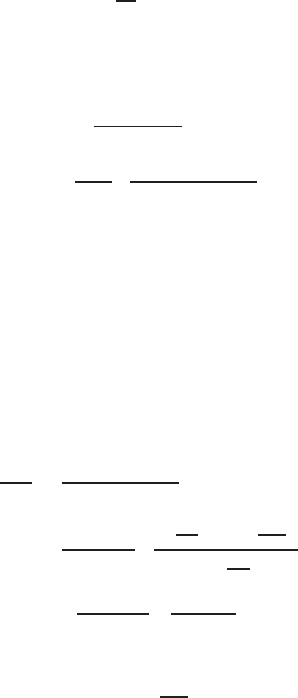
362 12 Electromagnetic Theory (Vector P otentials)
ε
1
+
= −RI
1
e
iωt
− L
d
dt
I
1
e
iωt
= −(R + iωL)I
1
e
iωt
. (12.44)
To find the current I
1
, we observe that around any closed loop, the total emf
must vanish, i.e., ε
1
+ ε
1
′
= 0 and therefore
I
1
e
iωt
= −iω
M
01
(R + iωL)
I
0
e
iωt
(12.45)
I
1
e
iωt
= −
M
01
L
iωL (R −iωL)
R
2
+ ω
2
L
2
I
0
e
iωt
. (12.46)
This is the expression for the eddy currents induced in the underground cir-
cuit. The secondary magnetic field generated by this induced current to the
receiving coil in the circuit is given by
ε
(s)
2
= −iωM
12
I
1
e
iωt
. (12.47)
Here M
12
in the mutual inductance between the underground circuit and the
receiving coil. The ratio of secondary emf and primary emf, i.e., ε
(s)
2
/ε
(p)
2
is
the em response function for the vertical coil and it is given by
ε
(s)
2
ε
(p)
2
=
−iωM
12
I
1
e
iωt
−iωM
02
I
1
e
iωt
=
M
01
M
12
M
02
)
i
ωL
R
1 −
iωL
R
1+
ωL
R
2
*
= −
M
01
M
12
M
02
α
2
+iα
l+α
2
(12.48)
where
α =
ωL
R
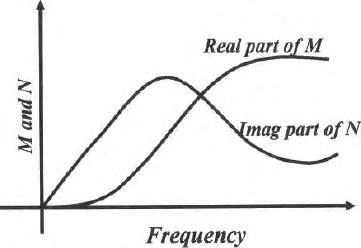
The electromagnetic response is a complex quantity (Fig. 12.9). The response
can be a measure either in the form of real and imaginary components or
in the form of amplitude and phase. The rea l part of the response is also
termed as the in phase component i.e., the c omponent which is in phase with
the primary field. The imaginary component, which is as real as the real
component, is termed as the out of phase or quadrature component. This
component will be 90
◦
out of phase with the primary field. The secondary
field generated by eddy currents in a medium of finite conductivity will always
differ with the primary field both in amplitude and phase. The real component
has the contributions both from the primary and secondary fields where as
the quadrature component or the phase angles come from the secondary field.
Thus the basic nature of the electromagnetic response in the presence of a
medium of finite conductivity can be explained using the concept of mutual
inductance.
12.5 Maxwell’s Equations 363
Fig. 12.9. Variation of the real and imaginary components of the electromagnetic
field in a simple mutual inductance model
12.5 Maxwell’s Equations
From the basic principles of electrostatics, magnetostatics and direct current
flow fields , we know
D=ε
E
B=µ
H (12.49)
J=σ
E
Here the basic electromagnetic vectors and scalars are given by (i)
E (elec-
tric field) in volt/meter (ii)
D (electric displacement) in coulomb/meter
2
(iii)
H (magnetic field) in ampere/meterorampereturn/m(iv)
B (magnetic
induction) in Weber/meter
2
(v)
J (current density) in ampere/meter
2
(vi)
ε (electrical permittivity) in farad/meter (vii) µ (magnetic permeability) in
henry/meter (viii) σ (electrical conductivity) in mho/meter.
According to Ampere’s law
I=
→
l
H.dl =
s
curl
H.n.ds (12.50)
where I is the current, H is the magnetic field and dl is the element of length
in a conductor carrying current.
Since
I=
J.n.ds,
we can write, applying Stoke’s theorem,
curl
H=
J. (12.51)
The electromotive force generated in a conductor is due to the rate of c hange
of number of lines of forces (or magnetic flux) and is equal to
364 12 Electromagnetic Theory (Vector P otentials)
ε = −
d
N
dt
. (12.52)
Since emf ε canbewrittenas
E.dl and magnetic flux as N =
B.n.ds, we,
therefore, can write
E.dl = −
∂
∂t
B.n.ds.
From Stoke’s theorem we write
⇒
s
curl
E.ds = −
∂
∂t
s
B.n.ds (12.53)
⇒ curl
E=−
∂
B
∂t
. (12.54)
This is the Maxwell’s first equation.
Current flow in a particular medium is the rate of flow of charge. Since
the current flowing out of a particular medium is the current loss inside, we
can write
J.n.ds = −
dq
dt
. (12.55)
Applying the divergence theorem we can write
div
Jdν = −
d
dt
ρdν (12.56)
where ρ is the volume density of charge. We can write
div
J = −
∂ρ
dt
. (12.57)
This is known as the equation of continuity. For uniform flow of current with
the source situated outside the region
div
J=0. (12.58)
Equation (12.57) is treated as the Maxwell’s fifth equation.
Since div
D =+ρ from (4.26), bringing the time derivatives on both the
sides, we get
∂
∂t
div
D
=
∂ρ
∂t
. (12.59)
It changes to
div
∂
D
∂t
=
∂ρ
∂t
. (12.60)
The equation of continuity changes to the form

12.5 Maxwell’s Equations 365
div
J=−div
∂
D
∂t
(12.61)
⇒ div
J+
∂
D
∂t
=0
⇒ div
J+
∂
D
∂t
=divcurl
H.
Because divergence of curl of a vector is always zero.
Hence
curl
H=
J+
∂
D
∂t
. (12.62)
This is Maxwell’s second electromagnetic equation.
Since
D =
Q
A
(Coulomb/meter
2
),
∂
D
∂t
is termed as the displacement cur-
rent. The rate of change of dielectric vector has the same dimension as
J. So
∂
D
∂t
will generate the magnetic field. Therefore the five Maxwell’s electromag-
netic equations are
i) curl
E=−
∂
B
∂t
, (12.63)
(ii) curl
H=
J+
∂
D
∂t
, (12.64)
(iii) div
B=0, (12.65)
(iv) div
D = ρ and (12.66)
(v) div
J = −
∂ρ
∂t
(12.67)
where (12.65) (12.66) and (12.67) are respectively taken from Chaps. 4, 5
and 6 . The respective equations are (5.49), (4.26), (6.18) and (12.57).
If there are impressed electric and magnetic currents the first two Maxwell’s
equations change to the form
curl
E=−
∂
B
∂t
−
M
i
(12.68)
curl
H=
J+
∂
D
∂t
+
J
i
. (12.69)
Using (12.49), we can write down the Maxwell’s (12.63) and (12.64) as
curl
E=−µ
∂
H
∂t
(12.70)
and
curl
H=σ
E+ ∈
∂
E
∂t
. (12.71)

366 12 Electromagnetic Theory (Vector P otentials)
12.5.1 Integral form of Maxwell’s Equations
Integral form of Maxwell’s equati ons are
(a)
curl E dv = −
∂
B
∂t
dv, (12.72)
(b)
curl
Hdv =
J+
∂
D
∂t
dv, (12.73)
(c)
div
J=−
∂ρ
∂t
dv, (12.74)
(d)
div
B = 0 and (12.75)
(e)
div
D=
ρ dv (12.76)
12.6 Helmholtz Electromagnetic Wave Equations
From equations (12.49) and (12.63) we can write
curl curl
E=−µ
∂
∂t
curl
H
= −µ
∂
∂t
)
σ
E+ ∈
∂
E
∂t
*
from (12.71).
Hence
grad div
E −∇
2
E=−µσ
∂
E
∂t
− µ ∈
∂
2
E
∂t
2
(12.77)
⇒∇
2
E=µσ
∂
E
∂t
+ µ ∈
∂
2
E
∂t
2
− grad div
E (12.78)
⇒∇
2
E=µσ
∂
E
∂t
+ µ ∈
∂
2
E
∂t
2
(12.79)
where div
E = 0 in a source free region (12.58) and is equal to
ρ
∈
where the
region contains the source. Equation (12.79) is the Helmholtz electromagnetic
wave equation.

12.6 Helmholtz Electromagnetic Wave Equations 367
Similarly it can be proved that
∇
2
H=µσ
∂
H
∂t
+ µ ∈
∂
2
H
∂t
2
. (12.80)
Since
Eand
H are electric and magnetic field vectors. They have three com-
ponents along the three mutually perpendicular coordinate axes. These wave
equations are valid for each component i.e.,
∇
2
H
x
= μσ
∂H
x
∂t
+ με
∂
2
H
x
∂t
2
. (12.81)
For very high frequency, where the displacement current dominates over the
conduction current. Therefore
∇
2
H
x
= µ ∈
∂
2
H
x
∂t
2
. (12.82)
At lower frequencies in the audio range, conduction current dominates over
the displacement current and the Helmholtz equation changes to the form
∇
2
H
x
= µσ
∂H
x
∂t
. (12.83)
Since both
Eand
H are vectors and having three components each, the-
oretically one has to determine six components to define the electromagnetic
field totally. In actual practice, for different types of source excitation, there
will b e some zero and non zero electric and magnetic vectors as shown in the
next chapter. We try to solve for the non zero
Eand
Hcomponents.
Alternatively if we express the electromagnetic field in terms of a vector
and a scalar potentials, the number of components to be determined will be 4
i.e., three components for one vector and one scalar. These vectors are termed
as vector potentials. One of the options for solving the electromagnetic bound-
ary value problems is to use these vector and scalars (please see Chap. 13). If
B, H and E are expressed respectively as curl A, curl A
′
and curl A
′′
,these
A, A
′
,A
′′
are termed as vector potentials because curl operates on a vector
and generates another vector. A brief introduction about the definition and
mathematical expressions for the vector potential is given in Chap. 5.
Since div
B = 0 always because the monopoles in magnetostatics do not
exist, we can write div
H = 0, because
B=µ
H. Since divergence of a curl of
a vector is always zero, we can write
H=curl
A (12.84)
where
A is a vector potential. div
E = 0 in a source free region. From (12.70),
we get
368 12 Electromagnetic Theory (Vector P otentials)
curl
E=−µ
∂
H
∂t
⇒−µcurl
∂
A
∂t
(12.85)
⇒ curl
E+µ
∂
A
∂t
=0. (12.86)
If curl of a vector is zero, then that vector can always be expressed in terms
of gradient of a scalar potential.
So
E+µ
∂
A
∂t
= −grad φ. (12.87)
Since
H=curl
A, we can write
curl curl
A=−µσ
∂
A
∂t
− σ grad φ
−µ ∈
∂
2
A
∂t
2
−∈grad
∂φ
∂t
=graddiv
A −∇
2
A. (12.88)
Since the vector potential is quite arbitrary, we can choose
grad div
A=−σ grad φ − ε grad
∂φ
∂t
(12.89)
which leads to
∇
2
A=µσ
∂
A
∂t
+ µ ∈
∂
2
A
∂t
2
. (12.90)
And
div
A=−σφ − ε
∂φ
∂t
. (12.91)
From (12.87), we get
div
E=−µ
∂
∂t
div
A −∇
2
φ = 0 (12.92)
and
∇
2
φ = µσ
∂φ
∂t
+ µ ∈
∂
2
φ
∂t
2
. (12.93)
Therefore, both vector and scalar potentials satisfy Helmholtz wave equations.
The connecting links between a vector and a scalar potential with electr ic and
magnetic fields are given by
H=curl
A (12.94)
E=−µ
∂
A
∂t
− grad φ. (12.95)
