Roy K.K. Potential theory in applied geophysics
Подождите немного. Документ загружается.


12.7 Hertz and Fitzerald Vectors 369
If electromagnetic field is harmonically varying field, i.e., E = Ee
iωt
and
H=He
iωt
, the Helmholtz wave equation changes to the form
∇
2
E=iωµσ
E+i
2
ω
2
µ ∈
E
=iωµ (σ +iω ∈)
E
= γ
2
E.
Here γ
=
iωµ (σ +iω ∈)
is termed as the propagation constant. Helmholtz
equations can be written shortly as
∇
2
E=γ
2
E
∇
2
H=γ
2
H (12.96)
∇
2
A=γ
2
A
∇
2
φ = γ
2
φ.
For audio frequency range the displacement current is negligible. Therefore
γ =
√
iωµσ. In the megahertz range γ =
iωµ (σ +iω ∈ and in the gigahertz
range γ =iω
√
µ ∈.
12.7 Hertz and Fitzerald Vectors
Hertz defined a vector potential
Aintheform
A=σ
Π+ε
∂
Π
∂t
(12.97)
where
Π is termed as the Hertz vector. Taking divergence on both the sides,
we get
σdiv
Π+ε
∂
∂t
div
Π=div
A
= −σφ − ε
∂φ
∂t
(12.98)
from (12.87). From (12.98) we get
φ = −div
Π. (12.99)
Equation (12.99) connects the Hertz vector with the scalar potential φ.
Because the divergence op erates on a vector and generates a scalar.
From (12.93) and (12.94) we can write
H=σ curl
Π+ε curl
∂
Π
∂t
=(σ +iω ∈)curl
Π (12.100)

370 12 Electromagnetic Theory (Vector P otentials)
and
E=−µσ
∂
Π
∂t
− µ ∈
∂
2
Π
∂t
2
+graddiv
Π
= −∇
2
Π + grad div
Π
= curl curl
Π. (12.101)
From (12.88 and 12.95), we write
∇
2
div
Π=µσ
∂
∂t
div
Π+µε
∂
2
∂t
2
div
Π. (12.102)
Here
∇
2
Π=µσ
∂
Π
∂t
+ µ ∈
∂
2
Π
∂t
2
. (12.103)
Therefore Hertz vector satisfies Helmoholtz wave equation. Equations (12.100)
and (12.101) are the connecting links b etween the Hertz vector and the electric
and magnetic fields.
Similarly, assuming
E=curl
A
′
where A
′
is the electric vector potential and
following the same procedure it can be shown that
curl
H − σA
′
− ε
∂
A
∂t
= 0 (12.104)
or
H −σA
′
+ ε
∂A
′
∂t
+gradψ (12.105)
where
H is the magnetic scalar potential. The vector potential F is, known as
Fitzerald vector which connects the E and H field through these two equations
H = curl curl
F (12.106a)
and
E=−iωµ curl
F (12.106b)
and will also satisfy the Helmholtz wave equa tion
∇
2
F=µσ
∂
F
∂t
+ µ ∈
∂
2
F
∂t
2
. (12.107)
Many of the electromagnetic boundary value problems can be solved using
Hertz or Fitzerald vectors. In that case the number of equations to be solved
is only three. Once a solution is obtained in
Πand
Fonecanmoveto
Eand
H
fields through these two pairs of connecting links i.e., (12.100), (12.101) and
(12.106a and b).
12.8 Boundary Conditions in Electromagnetics 371
12.8 Boundary Conditions in Electromagnetics
12.8.1 Normal Component of the Magnetic Induction
B is Continuous Across the Boundary in a Conductor
From Maxwell’s equation, we know that div
B = 0. From divergence theorem
we can write
div
B.dν =
B.n.ds. =0. (12.108)
Now assuming a small box of area ∆a and thickness ∆l across the bound ary
shown in the Fig. 12.10 we take the integration over the volume with an
approximation
(B
2
.n
2
+B
1
.n
1
)∆a + Contribution from the wall = 0.
Since the contribution from the walls is directly proportional to ∆l, its con-
tribution will be zero when ∆l = 0.
Therefore
B
2
.n
2
+B
i
.n
1
=0.
Since the normal vectors n
2
and n
1
on two opposite sides of the boundary
are in the opposite direction, i.e., n
2
= −n
1
, therefore
(B
2
− B
1
).n=0. (12.109)
In other words the normal components of the magnetic induction will be
continuous across the boundary.
12.8.2 Normal Component of the Electric Displacement
is Continuous Across the Boundary
Since divD = q
ν
,, we can write Gauss’s divergence theorem
v
div
Ddν =
s
D.n.ds. =
v
q
v
dv = q (12.110)
where q is the total charge and q
v
is the volume density of charge. Therefore,
we get as in the previous case (Fig. 12.11)
D
2
.n
2
+
D
1
.n
1
∆a = w∆a (12.111)
where w is the surface density of charge and
q=
v
q
ν
dv = q
ν
.∆l.∆a. (12.112)

372 12 Electromagnetic Theory (Vector P otentials)
Fig. 12.10. Normal component of the magnetic flux across the boundary with
different values of ε
±
,σ
±
,µ
Since n
2
= −n
1
as shown in previous case, we can write
D
2
−
D
1
.n=ω (12.113)
This equation shows that normal component D
n
of the vector
D is discontinu-
ous across the boundary due to accumulation of surface charge density w. At
the surface of a conductor the surface charge density dissipates very quickly.
Hence across the interface involving all but the poorest conductors, normal D
is continuous across th e boundary
Therefore
(D
2
.n
2
+D
1
.n
1
) = 0 (12.114)
(D
2
.n
2
− D
1
.n
1
) = 0 (12.115)
⇒ (D
2
− D
1
) .n=0
⇒ D
n
2
=D
n
1
(12.116)
Fig. 12.11. Normal component of the electric displacement across the boundary
with different values of ε, σ, µ

12.8 Boundary Conditions in Electromagnetics 373
12.8.3 Tangential Component of E is Continuous Across
the Boundary
From Maxwell’s equation curl
E=−
∂
B
∂t
,
we can write
s
∇×
E
nda −
∂B
∂t
.nda = 0 (12.117)
where n is the unit vector normal to the surface S. Applying the Stoke’s
theorem we can write
E.dl =
curl
E.n.da. (12.118)
Therefore
−
∂
B
∂t
.n.da =
E.dl =
E
2
.∆l +
E
1
(−∆l)
+contribution from the end where
E
2
.∆l and
E
1
.∆l are the tangential com-
ponents of
E in the medium 1 and 2 (Fig. 12.12). If we reduce the thickness
of the rectangular loop to zero such that
E
2
.∆t = 0. That brings the line
segments on the surface. The equation reduces to
−
∂B
∂t
.n∆t.∆l = (E
2
− E
1
) .∆l (12.119)
In the limit when the thickness of the strip ∆t = 0, the left hand side is zero,
so that acro ss the boundary
E
t
1
=E
t
2
or n × (E
2
− E
1
) = 0 (12.120)
where n is the unit vector normal to the boundary surface. In other words, the
tangential comp onent of the electric field is continuous across the boundary.
12.8.4 Tangential Component of H is Continuous Across the
Boundary
From Maxwell’s equation
curl
H=
J+
∂
D
∂t
,
Fig. 12.12. Tangential component of the electric v ector is continuous across the
b oundary with different values of ε, σ and µ

374 12 Electromagnetic Theory (Vector P otentials)
we can write
l
H.dl −
∂
D
∂t
.n.da =
J.n.da (12.121)
The contour of integration is the same as that shown in the previous case. By
using the component of H tangential to the boundary surface (Fig. 12.13) and
by proceeding to the limit of a contour of negligible height ∆l, we can write
nx (H
2
− H
1
)=
Lim
∆t → 0
∂
D
∂t
+
J
∆t = 0 (12.122)
for finite current density and bounded nature of D a nd its derivatives. There-
fore, the boundary condition for media of finite conductivity will be
nx(H
1
− H
2
) = 0 (12.123)
in the absence of any kind o f surface currents. Hence, the tangential compo-
nent of the magnetic field in continuous across the boundary.
12.8.5 Normal Component of the Current Density is Continuous
Across the Boundary
Currents entering and leav i n g an elementary box across the boundary span-
ning two conductive media consists partly of normal components and partly
of ta n gential components. As the thickness of the box across the boundary
tends to zero, the current crossing the interface may be computed either as
I=J
2
.n∆a or as I = J
1
.n.∆a
Thus the normal component of J, i.e., J
n
must be continuous across the bound-
ary. Hence
(J
2
− J
1
).n = 0 (12.124)
or
J
n
1
=J
n
2
Fig. 12.13. Tangential component of the magnetic field is continuous across the
b oundary of two media having different values of ε, σ,andµ
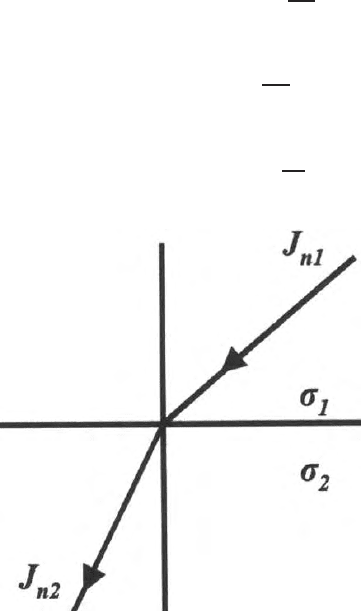
12.8 Boundary Conditions in Electromagnetics 375
12.8.6 Scalar Potentials are Continuous Across the Boundary
In electrostatics and magnetostatics problems
E=−grad φ and H = −grad φ
∗
where φ and φ
∗
are the scalar potentials. In the absence o f any source po tentials
φ and φ
∗
must be continuous across a boundary surface (Fig. 1 2.14). For the
work required to carry a small electric charge or a magnetic pole from infinity
to two adjacent points lo cated on opposite sides of the surface with negligible
distance between them must be the same, i.e.
φ
1
= φ
2
and
φ
∗
1
= φ
∗
2
.
Thus it is seen th at each and every Maxwell’s equation generate one bound-
ary condition in electromagnetics. Integral form of Maxwell’s equations for
generating the boundary conditions are
(f)
(n ×
E)ds = −
∂
B
∂t
div, (12.125)
(g)
(n ×
H)ds =
J+
∂
D
∂t
dv, (12.126)
(h)
(n.
J)ds = −
∂ρ
∂t
dv, (12.127)
Fig. 12.14. Normal component of current density J is across the b oundary
376 12 Electromagnetic Theory (Vector P otentials)
(i)
(n.
B)ds = 0 and (12.128)
(j)
(n.
D)ds =
ρdv (12.129)
where n is the vector normal to the surface. (12.130)
12.9 Poynting Vector
As electromagnetic waves travel through space from their source to the dis-
tant receiving points, there is a transfer o f energy from the source to the
receiver. There exists a simple and direct relation between the rate of this
energy transfer and amplitudes of this electric and magnetic field strengths of
the electromagnetic waves. This relation can be obtained from the Maxwell’s
equation a s follows. From the second Maxwell’s (12.62), we can write
J=curl
H −ε
∂
E
∂t
. (12.131)
This expression has the dimension of current density on both the sides. Mul-
tiplying both the sides of the (12.131) by
E, the modified equation has the
dimension of power per unit volume i.e.,
E.
J=
E.
∇×
H−∈
E
∂
E
∂t
(12.132)
And
∇.
E ×
H=
H.
∇×
E −
E.
∇×
H. (12.133)
Therefore
E.
J=
H.∇×
E −∇.
E ×
H−∈
E.
∂
E
∂t
. (12.134)
Fr om Maxwell’s fir st equation we get
∇×
E=−
∂
B
∂t
= −µ
∂
H
∂t
. (12.135)
Therefore
E.
J=−µ
H
∂
H
∂t
= −∈E
∂
E
∂t
−∇.
E ×
H. (12.136)
Since
H.
∂
H
∂t
=
1
2
∂
∂t
−2
H
12.9 Poynting Vector 377
and
E
∂
E
∂t
=
1
2
∂
∂t
−2
E
Therefore
E.
J=−
µ
2
∂
∂t
−
2
H
−
∈
2
∂
∂t
−
2
E
−
∇.
E ×
H. (12.137)
Integrating over a volume v,
v
E.
Jdv = −
∂
∂t
v
µ
2
H
2
+
∈
2
E
2
dv −
E ×
Hds
−
v
∇.
E ×
Hdv. (12.138)
Using Gauss’s divergence theorem, the last term of (12.138) changes from
volume integral to surface integral over the surfaces and encompassing the
volume v i.e.,
v
∇.
E ×
Hdv=
E ×
Hds. (12.139)
We can write (12.139) as
v
E.
Jdv=−
∂
∂t
v
µ
2
H
2
+
∈
2
E
2
dv −
E ×
Hds. (12.140)
As per basic definitions in electrical engineering, a conductor carrying current
I and h aving a voltage drop E per unit length will have a power loss of
E
I
watt per unit length. The power dissipated per unit volume is
E
I
A
=
E.
J. For
a homogeneous and isotropic medium
Eand
J will be in the same direction.
In general for an inhomogeneous and anisotropic medium.
Eand
Jmaynot
be in the same direction. Even the power dissipated will be the product of
J
and the component of
E along the direction of
J. Therefore the total power
dissipated in a volume will be
v
E.
J.dv. (12.141)
The expressions
1
2
∈ E
2
and
1
2
µH
2
are respectively the stored electrical and
magnetic energy per unit volume of the electric field.
The integral shows the dissipation of the total electrical and magnetic
energy. The rate of energy dissipation in the volume V must be equal
to the rate at which the stored energy in the volume is decreasing. The
term −
E ×
H ds represents the rate of flow of energy outward through
the surface enclosed in the volume V. The integral of
E ×
Hisameasureof
the energy out flow through that surface. It is seen that the vector is
378 12 Electromagnetic Theory (Vector P otentials)
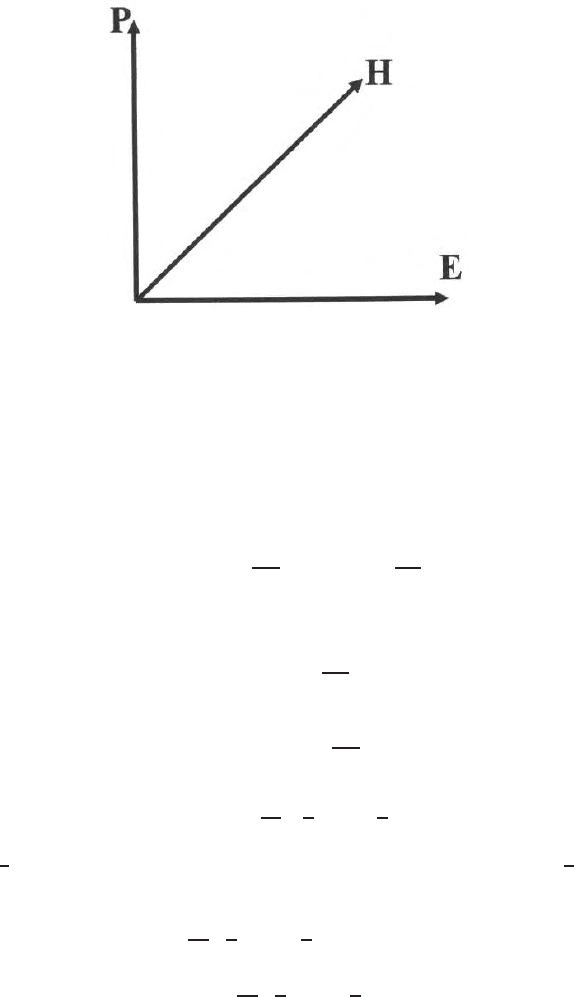
Fig. 12.15. Direction of propagation of a poynting vector
P=
E ×
H. (12.142)
The dimension of watt per square meter. It is a Poynting vector in electro-
magnetics (Fig. 12.15). The Poynting vector
P is directed at right angles to
the plane which contain
Eand
H. It is a cross product of E and H and the
energy flows at right angles to the plane which contains
Eand
H.
Now
∇.
E ×
H
=
H.
−µ
∂H
∂t
−
E
−∈
∂
E
∂t
. (12.143)
In a perfect dielectric where the conductivity is equal to zero, we get
∇×
E=−
∂
B
∂t
or
∇×
H=−∈
∂
D
∂t
.
So
∇.
E ×
H
= −
∂
∂t
1
2
µH
2
+
1
2
∈ E
2
. (12.144)
Here
1
2
µH
2
is the energy density associated with the magnetic field and
1
2
∈ E
2
is the energy density associated with the electric field. We therefore, can write
∇.
E ×
H
=+
∂
∂t
1
2
µH
2
+
1
2
∈ E
2
= 0 (12.145)
⇒
∇.
P+
∂
∂t
1
2
µH
2
+
1
2
∈ E
2
=0. (12.146)
This is the equation for the conservation of energy or the equations o f conti-
nuity in electromagnetic field. This equation is similar to the Maxwell’s fifth
