Roy K.K. Potential theory in applied geophysics

Подождите немного. Документ загружается.

Electrical Images in Poten tial Theory

In this chapter a brief idea about the concept of electrical image and its use in

computation of p erturbation potential in direct current ﬂow ﬁeld for layered

earth structures in bore hole geophysics are demonstrated. Necessary formulae

for computation of potentials a cross a horizontally stratiﬁed 3 layered bed

are given for two, three and seven(laterolog-7) electrode conﬁgurations. Th i s

approach for solution of the boundary value problems is restricted to problems

with simpler geometries.

11.1 Introducti on

Many of the potential problems in direct current p otential domains can be

solved using the concept of images. The analogy is drawn from optics. It

is shown that using more than one reﬂector one can get several series of

images, the way one gets the optical images in between the two mirrors. The

only condition required to satisfy is potentials must be continuous across the

boundary (or reﬂector). This technique for computation of potential is only

valid for plane boundaries (Dakhnov (1962), Keller a nd Frischknecht (1966).

Concept of images with spherical boundaries are available in. (Ramsay 1940),

Macmillan (1958).

11.2 Computation of Potential Using Images

(Two Media)

The potential at a point at a distance ‘r’ from a point current source embedded

in an inﬁnite and homogeneous medium of resistivity ‘ρ’isgivenby

φ =

Iρ

4π

(11.1)

330 11 Electrical Images in Poten tial Theory

where I is the current ﬂowing through the medium. In a semiinﬁnite medium

when the current electro de is on the surface,

φ =

Iρ

2π

. (11.2)

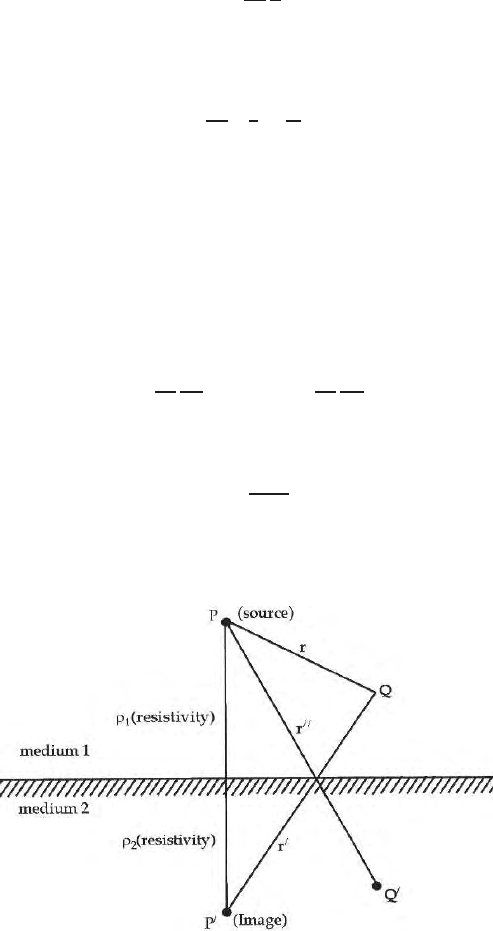
For two homogeneo us and isotropic semiinﬁnite media of resistivity ρ

and ρ

(Fig. 11.1) the p otential at a point P due to current source I is

φ =

4π



′



. (11.3)

Here I’ is termed as the electrical image of I at P. P and P

′

are at a same

distance from the boundary of the two media of resistivity ρ

and ρ

.Some

analogy can be drawn from the theory o f optics. This perturbation term,

originated from the concept of image and has to satisfy the basic boundary

conditions in direct curr ent electrical method i.e., (i) the potential on both

the media must be same on th e boundary and (ii) the normal component of

the current density is continuous across boundary.

These boundary conditions are φ

= φ

and



∂φ

∂n





∂φ

∂n



. (11.4)

Potential in a medium 2 due to a current source in a medium 1 is given by

′′

4πr

′′

(11.5)

where I

′′

is the reduced current strength and r

′′

is the distance of the point of

observation in the medium 2 from the source I in the medium 1.

Fig. 11.1. Electrical Image for a plane single b oundary between two semi inﬁnite

media of resistivity ρ

and ρ

respectively

11.2 Computation of Potential Using Images (Two Media) 331

In order to determine the strengths of the ﬁctitious current, we shall

apply the boundary conditions stated above. At the boundary since r = r

′

(Fig. 11.1), we get

(I + I

′

)=ρ

′′

. (11.6)

Applying the second boundary condition, we get



∂φ

∂n



4π



∂

∂r





∂r

∂n

∂

∂r

′



′



∂r

′

∂n

= −

4π



′

′2

′



(11.7)

and

∂φ

∂n

4π

∂

∂r



′′



= −

′′

4πr

′′2

′′

. (11.8)

A t the boundary r = r

′

and

= −

′

. Equating (11.7) and (11.8), we get

I −I

′

′′

. (11.9)

Equations (11.6) and (11.9) yields

′

− ρ

+ ρ

I=K

I (11.10)

and

′′



1 −

− ρ

+ ρ



2ρ

+ ρ

I=(1−K

)I. (11.11)

and (1−K

) a re termed respectively as reﬂection factor and transmission

factor. Potentials in the ﬁrst and second media ar e respectively given by

4π



′



(11.12)

4π

(1 − K

) . (11.13)

We can now compare electrical images with o ptical images. Current source

should be replaced by a source of light and boun d ary between the two media

should be replaced by a mirror of reﬂection coeﬃcient K

and transmission

coeﬃcient (1−K

). If the light source is seen from medium 1, one can measure

the intensity of light due to the source and the reﬂected light intensity I

′

and

coming from the image point P

′

. I f the light source is viewed from medium 2,

one will see the light with reduced intensity (1 − K

)I.

332 11 Electrical Images in Poten tial Theory

11.3 Computation of Potential Using Images

(for Three Media)

A simple approach for computing potential ﬁeld using the theory of electrical

images is discussed. The use of images, has major application in plane bound-

ary problems. Concept of image can also be applied for spherical boundary

problem. The potential ﬁeld can be found out very easily for a medium with

two plane and parallel boundaries using this method. The problem is one of

determining the potential function for three regions designa t ed as medium

1,2and3havingresistivitiesρ

, ρ

and ρ

. The regions are separated by two

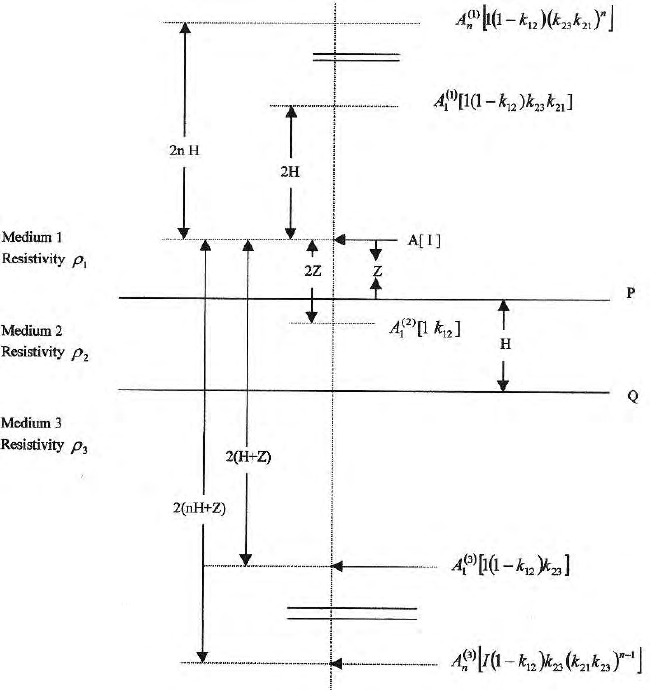
plane parallel boundaries P and Q (Fig. 11.2). The general set up and the

po sition of the diﬀerent series of current images and their strengths, when

the current source is situated in medium 1 at a point A, are shown In the

Fig. 11.2. Here H is the thickness of medium 2, the target bed, Z, is the dis-

tance of the current electrode from the interface P, between medium 1 and 2

; D, is the distance between the current and potential electrodes. K

is the

reﬂection factor for medium i and j, where K

=(ρ

− ρ

)/(ρ

+ ρ

),iandj

varies between 1 2 and 3 and I is the current strength. For determining the

potential at a point, we have to ﬁrst ﬁnd out the potential at a point due to

the source irrespective of whether the source and the observation point (s) are

in the same or in diﬀerent medium (or media). Next the contributions from

series of images are computed and are algebraically added up.

Distribution of image current sources in a medium with two parallel plane

boundaries; the original current source A [I] in medium 1 are shown in the

Fig. (11.2). These series of images originated to satisfy the two boundary

conditions at the interfaces, i.e.,

1) φ = φ

′

2) J

′

where φ and φ

′

are the potentials and J

and J

′

are the normal components of

the current densities on both the sides of the interface. More than one series

of images are generated for any current source placed in any medium.

Any current source placed in medium 1 at a distance z from the interfac e P

has to satisfy the boundary conditions at P. By introducing the image source

(2)

of strength IK

the boundary condition at P is satisﬁed. The potential

function in medium 2 will be the same as it would be in a fully inﬁnite and

homogeneous medium with a source of re du ced intensity I(1 −K

Now, to satisfy the boundary condition at Q, another ﬁctitious current

source A

(3)

in medium 3 at a distance 2 (H + Z) from the current source at

A has to be introduced. The strength of this source will be 1(1 − K

Addition of this second ﬁctitious source in dicates that the boundary con-

ditions at P is no longer valid. A third image at the point A

(1)

in the ﬁrst

medium is needed to satisfy the boundary conditions. The strength of the

image source will be I (1 − K

and located at a distance 2(2H + Z)

from the image A

(3)

in the third medium and 2H from the original current

11.3 Computation of Potential Using Images (for Three Media) 333

Fig. 11.2. Shows the formation of images in a layered medium

source A. When the addition of third image A

(1)

satisfy the boundary con-

ditions at P, the boundary conditions at the interface Q becomes invalid. To

restore this, another image source A

(3)

of strength I(1 − K

has to be introduced in the third medium at a distance 2(2H + Z) from the

original current source at A.

The process of developing image sources will co ntinue inﬁnitely for bal-

ancing out the proceeding boundary condition. This process will create two

inﬁnite series of image sources one in medium 1 and other in medium 3.

In medium 1, the generalized expression of the image current source are

I(1 − K

)(K

)

and are located at a distance 2nH from the original

current source at A and in medium 3, the expression of image current sources

are I(1 − K

)

n−1

at a distance of 2(nH + Z) from the source

current. Dep ending on the position of the electrodes current image sources are

334 11 Electrical Images in Poten tial Theory

used for calculation of potentials. For example if potential current electrodes

are in medium 1 , the images in medium 1 are not considered.

Proceeding in a same way, it can be shown that if we have a current

source in medium 2 , then there will be four series of images. Considering a

point source electrode at a distance Z from the interface P, the generalized

expressions for image sources are described below.

a) First series of images in the medium 1 with strength IK

)

n−1

a distance 2(n − 1)H + Z from the current source.

b) Second series of images in the medium 1 with strength I(K

)

at a

distance 2nH from the current source.

c) First series of images in the medium 3 with strength IK

)

n−1

a distance 2(nH − Z) from the original current source.

d) Second series of images in the medium 3 with strength I(K

)

Proceeding in the similar way, expression for image sources when the cur-

rent electrode is in medium 3 can be found out. In the following section a

set of general expressions of potentials are given considering one current and

one potential electrode. They cover all possible combination that can appear

considering two electrodes and three media with two parallel boundaries.

11.4 General Expressions for Potentials Using Images

To generate these expressions for potentials we have taken a 3 layered earth

model with upper shoulder bed resistivity ρ

(medium 1), target bed resistivity

(medium 2) and lower shoulder bed resistivity ρ

(medium 3) ; H is the

target bed thickness, distance of current electrode z is calculated from the

interface between medium 1 and medium 2, when the current electrode is

in the medium 1. The distance z is also calculated from the interface of the

medium 2 and medium 3 when the current electrode is in the medium 3, D

is the electrode separation, K

, K

are the reﬂection coeﬃcients where

=(ρ

−ρ

)/(ρ

−ρ

)andK

=(ρ

−ρ

)/(ρ

+ ρ

) and I is the current

sent. In some expressions ± sign is given. This is due to the relative positions

of the electrodes in a particular medium. Basic equation for calculation of

potential measured at the borehole axis (r = 0) due to one point source

current electrode can be written as follows.

a) Expressions of potential at a point when both the electrodes are in

medium 1

4π

)

(2Z ± D)

+(1− K

∞



n=1

)

n−1

(2nH + 2Z ± D)

(11.14)

b) Expression of potential at a point when the current electrode is in mediu m

1 and the potential electrode is in medium 2

11.4 General Expressions for Potentials Using Images 335

4π

(1 −K

)

∞



n=0

(2nH + D)

∞



n−1

)

(2nH + 2Z −D)

(11.15)

c) Expression of potential at a point when the current electrode is in medium

1 and the potential electrode is in medium 3

4π

(1 −K

)(1− K

)

∞



n=0

)

2nH + D

(11.16)

d) Expression of potential at a point when the current electrode is in mediu m

2 and the potential electrode is in medium 1

4π

(1 − K

)

∞



n=1

)

(2nH + D)

∞



n=1

)

n−1

{2(n− 1) H + 2 (H − Z) + D}

(11.17)

e) Expression of potential at a point when both the electrodes are medium 2

4π

)

∞



n=1

)

n−1

{2(n− 1) H + 2Z ±D }

∞



n−1

)

n−1

{2(n− 1) H + 2 (H −Z) ∓ D}

∞



n=1

)

2nH ± D

∞



n=1

)

(2nH ∓ D)

(11.18)

f) Expression of potential at a p oint when the current electrode is in medium

2 and the potential electrode is in medium 3

4π

(1 −K

)

∞



n=1

)

(2nH + D)

∞



n=1

)

n−1

{2(n− 1) H + 2Z + D}

(11.19)

g) Expression of potential at a point when the current electrode is in medium

3 and the potential electrode is in medium 1

4π

(1 + K

)(1+K

)

∞



n=0

)

(2nH + D)

(11.20)

336 11 Electrical Images in Poten tial Theory

h) Expression of potential at a point when the current electrode is in mediu m

3 and the potential electrode is in medium 2

4π

(1 + K

)

∞



n=0

)

(2nH + D)

− K

∞



n=1

)

n−1

(2nH + 2Z −D)

(11.21)

i) Expressions of potential at a p oint when both the electro des a re in

medium 3

4π

)

−

2Z ± D

− (1 − K

∞



n=1

)

n−1

(2nH + 2Z ± D)

(11.22)

11.5 E x pressio ns for Potentials for Two Electrode

Conﬁguration

For full space with two plane parallel boundaries there will be in total ﬁve

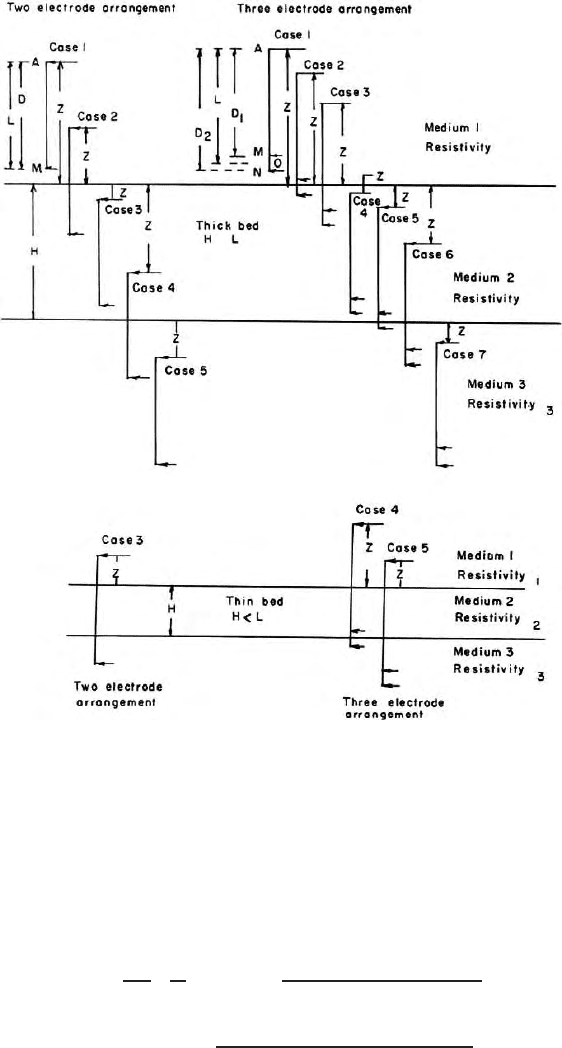
cases for two electrode conﬁgurations (Fig. 11.3) when target bed thickness

is greater than tool length. If target bed thickness is less than tool length a

special case arises (Fig. 11.3). In any set up the total number of tool p ositions

with respect to target bed are ﬁve. Expressions for Potential for diﬀerent cases

are given below. For two-electrode conﬁguration, the return current electrode

and other potential electrode are theoretically assumed at inﬁnite distances. In

reality, they are kept away from the electrode system AM. Tool conﬁguration is

shown in the Fig. 11.3 and AM (=D) is the electrode separation. Expressions

for potentials for ﬁve cases are

Cases for thick bed (H > L)

Case 1:

4π

)

2Z − D

+(1− K

∞



n=1

)

n−1

(2nH + 2Z − D)

(11.23)

Case 2:

4π

(1 − K

)

∞



n=0

)

(2nH + D)

∞



n=1

)

n−1

(2nH + 2Z −D)

(11.24)

11.5 Expressions for Potentials for Two Electrode Conﬁguration 337

Fig. 11.3. Three media with two plane parallel boundaries; ﬁrst and third media

are semiinﬁnite media; second medium has ﬁnite thickness; two electrode (AM) and

three electrode (AMN) set up are approaching and crossing the two boundaries;

5 and 7 set of images are respectively formed as shown; thin bed case, i.e., bed

thickness less than the electrode separation are presented

Case 3

4π

)

∞



n=1

)

n−1

{2(n− 1) H + 2Z + D}

∞



n=1

)

n−1

{2(n− 1) H + 2 (H − Z) − D}

338 11 Electrical Images in Poten tial Theory

∞



n=1

)

(2nH + D)

∞



n=1

)

(2nH −D)

(11.25)

Relative tool po sitions for normal and lateral electrode

Case 4:

4π

(1 −K

)

∞



n=1

)

(2nH + D)

∞



n=1

)

n−1

{2(n− 1) H + 2Z + D}

(11.26)

Case 5:

4π

)

−

(2Z + D)

− (1 −K

∞



n=1

)

n−1

(2nH + 2Z + D)

(11.27)

Sp ecial case for thin bed (H < L):

Case 3:

4π

(1 −K

)(1− K

)

∞



n=0

)

(2nH + D)

(11.28)

Apparent resistivity (ρ

) at each point of the run is computed using the for-

mula

=4π.AM.

(11.29)

where, AM is the tool length and I is the current intensity.

11.6 E x pressio ns for Potentials for Three Electrode

Conﬁguration

In case of lateral o r three-electro de arrangement, the total cases in any setup

are seven. Both thick bed (H > L)andthinbed(H< L) cases a re con-

sidered. The diﬀerent positions including the special cases for thin bed are

shown in Fig. 11.3 Bed thickness less than potential probe separation (MN)

is not considered, as the separation is very less compared to to o l length. Tool

conﬁguration is shown in Fig. 11.3 w h ere A is the current electrode and M,