Рубин А.Б. Современные методы биофизических исследований (Практикум по биофизике)

Подождите немного. Документ загружается.

Функцию

/ (со, а) называют

стабилизирующим

множителем.

Выбор оптимальной функции f (со, а) зависит от особенностей

конк-

ретной

задачи и во многих случаях осуществляется с помощью чис-

ленного эксперимента. Примеры стабилизирующих множителей:

(со,

а) =

е-•«•

-'; /, (to, ее) =

(<о)

око

Не

останавливаясь на

других

возможных

подходах

к решению

поставленной

задачи, необходимо отметить, что в последнее время

связи с бурным развитием цифровой техники появилось большое ко-

личество работ, посвященных выделению

«идеального»

спектра из

зарегистрированного на реальном приборе. В частности, предложен

метод, с помощью которого может быть получена принципиально важ-

ная

спектроскопическая информация без перехода к идеальному

спектру, что отвечает увеличению разрешения не бесконечно, а

только в несколько раз, что равносильно записи спектра на прибо-

ре более высокого класса. Такая необходимость возникает зачастую

при

работе на стандартных приборах, когда световые потери из-за

малых размеров образца, потери на окнах криостата, поляризаторе

т. п. вынуждают проводить измерения при больших щелях, что

заведомо не

дает

возможности использовать разрешение прибора.

Анализ кинетической информации

Одним

из распространенных биофизических подходов при изучении

пространственно-временной

организации и молекулярных механиз-

мов первичных процессов фотосинтеза является

кинетический

метод.

В основу экспериментальных исследований положена регистрация

процесса релаксации изучаемой системы к равновесному состоянию

после выведения ее из этого состояния каким-либо внешним воз-

действием. В фотобиологических исследованиях в качестве внеш-

него воздействия, как правило, используют возбуждающий свет,

хотя в общем

случае

это

могут

быть скачок температуры, давления,

импульсы электрического или магнитного поля. В процессе кинети-

ческих исследований следят за изменениями структурно-конформа-

ционных

состояний молекул и надмолекулярных

структур

либо

используют эти изменения в качестве индикаторов для реакций, ин-

тересующих исследователя.

Изучение кинетик поведения сложных биологических систем ба-

зируется на построении и анализе математических моделей, в ко-

торых скорость изменения концентрации различных составных ком-

понентов

выражена через скорость отдельных элементарных реак-

ций,

принимающих участие в их образовании или исчезновении.

В процессе построения модели проводят уточнение характера свя-

зей

между

взаимодействующими компонентами, а также значений па-

раметров, которые на первых этапах

могут

носить весьма ориенти-

ровочный

характер. Последующая проверка справедливости моде-

341

ли состоит в таком варьировании значений параметров, которое мак-

симально приблизило бы поведение модели к оригиналу.

Модельное описание системы, состоящей из различных взаимодей-

ствующих компонентов, в общем виде сводится к составлению и ана-

лизу системы из N дифференциальных уравнений первого порядка:

/dt

, .... Слг,

k-^ki,

..., k

lAt

fN(c

, .... c

, К fe

, .. , k

(IX.6.3)

При

этом предполагают, что каждое i-e соединение из общего

их числа характеризуется значением концентрации С\ (i = 1, 2,

.... N), которое изменяется во времени c

— c

(t) в

результате

взаимодействия t-ro соединения с любым из остальных. Константы

скорости этих взаимодействий обозначены k

..., км-

Правые части уравнений (IX. 6.3) в зависимости от характера

протекающих в системе процессов

могут

содержать как линейные,

так

и нелинейные члены относительно переменных с

(t), ...,

(t),

а также члены, явно зависящие от времени. В этом

случае

аналити-

ческий

анализ системы

(IX.6.3)

затруднен и решение производится

численными

методами с использованием быстродействующих ЭВМ.

Отождествление полученных результатов с экспериментальными

данными

затруднено из-за наличия нескольких наборов коэффици-

ентов, удовлетворяющих экспериментальным данным с заданной

степенью точности. Для преодоления этих трудностей, как прави-

ло,

максимально упрощают математическое описание системы и по-

иск

решения. С этой целью экспериментально создаются условия,

которых модель поведения системы имеет линейный характер.

Например,

создается избыток одного из компонентов, концентра-

ция

которого изменяется во времени и может входить в дифферен-

циальные уравнения в виде константы. При этом скорости биомоле-

кулярных реакций с участием этого компонента становятся зависи-

мыми лишь от одного переменного и система уравнений

(IX.6.3)

становится линейной. Решение системы дифференциальных

уравнений сводится к линейной комбинации экспоненциальных

функций

вида Л

;

е~*''' (i =1, ..., М), где А

(

соответствует локаль-

ным

концентрациям реагентов, а Я, характеризует скорости проте-

кающих реакций.

Таким

образом, при исследовании кинетики переходных про-

цессов в биофизических исследованиях встает задача разложения

экспериментально зарегистрированной кривой, представимой в ви-

де

/(/)=

+6(«.

на

отдельные компоненты и определения по форме кривой неиз-

вестных коэффициентов A

и Л,;. В общем

случае

количество ком-

понентов

М также неизвестно и подлежит определению. Задача ос-

342

ложняется наличием характерных для экспериментальных сигна-

лов особенностей: неизвестной постоянной составляющей С и пара-

зитной

шумовой помехи £ (t).

Следует

подчеркнуть, что поставленная задача неустойчива к

малым возмущениям исходных данных, т. е. является некорректно

поставленной задачей. Для примера рассмотрим на интервале

[О,

21 две таблично заданные функции:

где U = Hx

\ H =

0,004;

i = 0,1, ..., 499.

Расчет на ЭВМ среднеквадратичного отклонения функции, со-

стоящей из

трех

компонентов, от функции g,-, состоящей из

двух

компонентов,

дал следующий

результат:

499

7.2

=0,0041.

что составляет менее 0,15 % от суммарной амплитуды сигнала.

При

сопоставлении графиков этих функций такое отклонение

визуально не различимо.

Все известные методы разложения с использованием ЭВМ мож-

но

разделить на три группы. К

первой

группе

относятся методы, ана-

логичные методам ручной обработки, реализованные на ЭВМ. Их

идея основана на анализе кривой переходного процесса при ее изо-

бражении в полулогарифмическом масштабе. При этом одноэкспо-

ненциальная

кривая представляет собой прямую линию. Если кри-

вая состоит из суммы экспонент, то по

хвосту

этой кривой (в части,

где влияние быстрых компонентов максимально) определяют пара-

метры наиболее долгоживущей составляющей, затем вычитают ее

из

суммарной кривой и процедуру повторяют с оставшейся частью.

Недостатки этого метода как при ручной, так и при машинной обра-

ботке заключаются в низкой точности и плохом разрешении ком-

понентов.

При наличии в исследуемом сигнале нескольких

экспо-

нент с близкими параметрами этот

подход

может привести к пол-

ному искажению результатов.

Методы

второй

группы

основываются на различных интеграль-

ных преобразованиях, таких, как преобразования Фурье, Лапласа,

вычисление моментов. Общей особенностью методов я,вляется то, что

на

одном из этапов вычислений проводят интегрирование от нуля до

бесконечности. Цель этой операции — сведение задачи разложения

экспоненциальной

функции к более простым задачам. Но именно ис-

пользование интегрирования приводит к одному из основных недо-

статков метода — к увеличению ошибок вследствие ограниченности

реальных сигналов. В итоге становится принципиально невозможным

определить отдельные компоненты при выборе ограниченного

343

участка суммарной кривой. Общим недостатком второй группы мето-

дов является плохая устойчивость к шумовым помехам.

В частности, в

методах,

основанных на преобразовании Фурье

(например,

методе

Гарднера и аналогичных ему), информация об

отдельных компонентах заключена в кривой, представляющей со-

бой

в идеальном

случае

сумму

б-функций, высота которых пропор-

циональна

отношению Л,/Я,(, а положение — \n\

. Вследствие ог-

раниченности

точности задания суммарной кривой в области интег-

рирования

происходит уширение максимумов, соответствующих от-

дельным компонентам, а также появляются паразитные осцилля-

ции

между

максимумами. К недостаткам также относится необхо-

димость ввода данных в ЭВМ в полулогарифмическом масштабе.

третьей

группе

относятся наиболее эффективные и развивае-

мые в настоящее время методы, которые условно можно назвать

сиггебраическими.

В основе их лежит решение линейных алгебраичес-

ких уравнений специальными регуляризационными методами.

Известны

попытки решения задачи декомпозиции непосредствен-

но

с помощью

метода

наименьших

квадратов.

Для случая

двух

ком-

понентов

невязка (S) имеет вид

Минимум

этой величины находят из условия равенства нулю про-

изводных невязки по соответствующим параметрам. Прямое решение

получаемых уравнений сопряжено со значительными трудностями

вычислительного характера и

требует

применения самых современ-

ных быстродействующих ЭВМ.

Ниже

описан один из методов анализа кинетической информа-

ции,

программная реализация которого включена в состав пакетов

прикладных программ автоматизированных комплексов на основе

микроЭВМ

«Электроника-60», а также ЭВМ СМ-4. В процессе ана-

лиза определяются показатели экспонент, амплитуды, среднеквадра-

тичная

ошибка.

Для простоты рассмотрим сущность метода на примере, когда

переходный процесс может быть представлен суммой

двух

экспо-

нент:

где показатели Л,

и %

действительны и различны. Целью анализа

является

определение значений параметров k

< ^i. Аг< когда

значения

функции / (t) заданы таблично на равномерной дискретной

сетке аргумента t.

Легко проверить прямой подстановкой, что функция / (t)

удов-

летворяет дифференциальному уравнению

[<d/dfl - XJ [(d/dO

-X,] f(t) = 0. (I X .6.4)

344

Первый

этап анализа состоит в определении значений парамет-

ров Xj и Х

, когда решение (IX. 6.4) известно и задано таблично.

Решая

(IX.6.4)

относительно [(d/dt) — %

] f (t) и производя

интегрирование,

получаем

/«-/(/„)=

JV(*)d<,

(IX.6.5)

i. t,

где t

— начальное значение аргумента, В, — константа, опре-

деляемая параметрам А

1г

Выбирая достаточно произвольно область интегрирования и ин-

тегрируя (IX. 6.5) от t

до некоторого значения t

из области зада-

ния

t, получаем при i = I, ..., N набор линейно независимых урав-

нений

(IX. 6.6), которые для

удобства

запишем в виде

бе*

=(e

'i — e*

'*)At.

(IX.6.6)

где

J/(0df;

6Д

=/<*,)-/(*,).

Аналогичными рассуждениями можно получить еще один набор

линейно

независимых уравнений в виде

В^бе^'г+^Л — б/

= 0,

(IX.6.7)

где 6e*"''=(e

'*—е*«'.)До.

Аналогично предыдущему случаю В

определяется параметрами

, X

. При наличии в анализируемом сигнале шумовой поме-

хи система трансцендентных уравнений (IX. 6.6), (IX. 6.7) может

быть несовместна. В связи с этим получение приближенного реше-

ния

набора уравнений производят методом наименьших квадратов.

Минимизируя

стандартным образом длину вектора невязок, можно

получить уравнения относительно параметров Х

и к

, но прямое их

решение

будет

затруднительно. В связи с этим строится итерацион-

ная

процедура, в соответствии с которой последующие приближе-

ния

параметров

Я,<"+

и Ц

п+1)

определяются через предыдущие

\{") и Ц

п)

. Окончательная расчетная формула для

имеет вид

Вычисление А,<

» производят также по этой формуле после заме-

ны

п)

наЦ"+').

345

Начальное приближение

итерационном процессе задается

по

формуле

случае

сходимости итерационной процедуры

за

искомые

принимаются значения

К["

)

и К[°°

)

пределов последовательностей

X,<j

и К[

п)

Значения амплитуд

и А

рассчитывают методом

на-

именьших квадратов

по

вычисленным значениям параметров

- Для

улучшения сходимости итерационного процесса

расчет-

ные формулы вводят инкремент

по

формуле

При

использовании описанной методики

для

анализа экспери-

ментальных данных проводят предварительную обработку, пред-

ставляющую собой анализ

устранение «выпавших точек»,

обу-

словленных случайными ошибками. Точка считается «выпавшей»,

если

она

отличается

от

двух

соседних более

чем на 20 %.

Осуществ-

ляется предварительное сглаживание данных

помощью кубиче-

ской

параболы

у = а + Ьх + ex

-f dx

Каждый внутрен-

ний

член массива данных объединяется

тремя справа

от

него

тремя слева. Через семь последовательно расположенных точек

ме-

тодом наименьших квадратов проводят параболу

значение сред-

ней

точки заменяют значением параболы

этой точке. Сглаживание

трех

первых

последних точек проводят аналогично,

но

парабола

строится несимметрично относительно

них.

Компьютерный анализ спектров ЭПР спин-меченых белков

В основе метода

лежат

избирательное введение

биологический

объ-

ект стабильного иминоксильного радикала (спиновой метки)

и ана-

лиз спектров

ЭПР

этого радикала

при

различных условиях окру-

жающей среды. Спектры

ЭПР

спиновых меток чувствительны

вращательной подвижности

ориентации радикалов,

на их

форму

влияют броуновское вращение, внутренняя конформационная

под-

вижность

локальная

структура

белковой макромолекулы.

В соответствии

теорией основным фактором, определяющим фор-

му спектра ЭПР данного нитроксильного радикала является распре-

деление

его

неспаренного электрона

по

(N—0)-фрагменту молеку-

лы. Спин-гамильтониан

для

трехсантиметрового диапазона

СВЧ-

поля

малой мощности при условии низкой локальной концентрации

парамагнитных центров

медленного прохождения через резонанс-

ные условия имеет следующий

вид:

pSGH+yhSAI,

346

где

Н —

величина магнитного поля;

S —

оператор спина электро-

на;

/ —

оператор спина ядра азота

N; А и G — тензоры

сверх-

тонкой

структуры

(СТС) и

g-фактора

главными

значениями

, А

и g

, g

соответственно;

р — магнетон Бора, А —

постоянная

Планка,

у —

гиромагнитное отношение.

Первый

член

описывает энергию магнитного взаимодейстия свободного электро-

на

(N —

О)-фрагмента нитроксильного радикала

внешним

маг-

нитным

полем. Второй член

соответствует

взаимодействию элект-

рона

ядром азота

(N —

О)-фрагмента радикала. Вследствие того

что спин ядра

равен единице,

СТС

спектра представляет собой

три линии равной интенсивности, расстояния

между

которыми рав-

ны

зависят

от

ориентации

(N —

О)-группы относительно внеш-

него магнитного поля. Рассмотрим

(рис. 149, А)

введенную

для

удобства

анализа систему координат,

ось х

которой совпадает

с на-

правлением

(N —

О)-связи,

а ось z — с

направлением

2р

я-орбита-

ли атома азота.

Углы

ф и в

определяют направление внешнего поля

Н.

Эта

система координат практически совпадает

собственной

сис-

темой координат нитроксильного радикала,

которой

А- и

G-тен-

зоры диагональны

характеризуются тремя собственными значе-

ниями:

, А

и g

, gy, g

случае

магниторазбавленного монокристалла того

или

иного

нитроксила спектры ЭПР представляют собой триплеты одинаковой

интенсивности.

При

этом если

ось х, у или г

направлена вдоль

маг-

нитного поля

Н, то

расстояние

между

крайними пиками триплета

будет

соответственно

2А

, 2А

2А

Для

спектров нитроксильных

радикалов

водном растворе

усред-

ненное

расстояние

ними

пиками

•мл-

яние

между

край-

ц /

СТС

определяется

» Ли

РИС.

149.

Схема N—О-фрагмента

ни-

троксильного радикала

(А) и

модель

быстрого анизотропного ротатора

на

медленном изотропном ротаторе

(5)

Рис.

150.

Спектры

ЭПР

спин-метки:

— в водной растворе, б — в порошковом

состоянии,

в — ковалентио связанной с

белковой молекулой в нормальных усло-

виях

(20°С,

раствор сахарозы, остальные

объяснения

см. в тексте)

347

как

2а

(рис. 150), где

(1/3)

(А

+ A

+ А

Для «порошко-

вых>

спектров расстояние

межлу

крайними широкими пиками

(КШП)

остается равным

2А

, в то

время

как

центральная часть

спектра есть

результат

суперпозиции вкладов

от

составляющих

у,

которые спектрально

не

разрешаются.

Ввиду

близости значе-

ний

, g

и g

положения центров спектров

х-,

у-

или z-ориен-

тацией мало отличаются

и в

трехсантиметровом диапазоне СВЧ

влияют только

на

центральную часть спектра.

связи

этим весь

анализ спектров ЭПР нитроксильных радикалов

для

статического

или

динамического вариантов ведется через изменение компонента

СТС

спектра

(в

соответствии

принятыми обозначениями

2 A

Как

показывает эксперимент, при использовании нитроксильных

радикалов

для

исследования динамики поведения макромолекул

спектры ЭПР хорошо описываются моделью анизотропного ротатора

на

изотропном ротаторе (рис. 148,

Б).

Принципиальную роль

для

развития методики, описанной далее, играет

то

обстоятельство,

что

влияние

на

спектр ЭПР быстрых вращений радикала относительно

белковой молекулы

медленных вращений комплекса белок

—

мет-

ка

удается

разделить

на две

аддитивные составляющие. Быстрое

анизотропное вращение радикала

с (т

10~

с)

приводит

к то-

му,

что

компоненты СТС частично усредняются: А

-*-А

;

—*"•"»»

—*•

Медленное диффузное движение макромолекулы

(т

> 10~

с)

приводит

дополнительному

сдвигу

расстояния

между

КШП

центру спектра:

АА

(2Л

-2Л

)

(2A

-2Al),

где первая составляющая

соответствует

изменению расстояния меж-

ду КШП, обусловленному движением спин-метки относительно бел-

ка,

вторая определяется изотропным движением белковой молеку-

лы. Учитывая природу ковалентного связывания нитроксильного

радикала

белком, рассматривают аксиально-симметричный

слу-

чай, при котором z-компонент СТС спектра ЭПР

соответствует

А ц,

а неразрешаемые

х- и

^-компоненты

соответствуют

(соответст-

венно

вводят обозначения

Лц,

А, = А

= A\).

Количественно движение метки относительно белка характеризуется

параметром порядка

S==(l

-fl

)/H,-a

(IX.6.8)

Таким

образом,

спектре ЭПР нитроксильного радикала, при-

соединенного

белковой молекуле, содержится информация

сред-

ней

амплитуде переориентации

средних

частотах,

определяющих

спектр ЭПР.

настоящему времени прямая задача ЭПР-спектроско-

пии

нитроксильных радикалов

—

моделирование спектров

ЭПР

348

для заданной модели

движения нитроксила —

решена, созданы соот-

ветствующие программы

расчета на ЭВМ. Разра-

ботаны методические

подходы, позволяющие

получить из эксперимен-

тальных спектров пара-

метры, необходимые для

теоретических расчетов,

а также информацию для

выбора адекватной моде-

ли вращения радикала.

Процесс

моделирова-

ния

спектров начинается

с ввода в диалоговом ре-

жиме

входных

парамет-

ров:

констант СТС и

значения

g-фактора для

используемого типа ра-

дикала, параметра по-

рядка s, времени пере-

ориентации белка т

ширины

линий спектра

(подбирается варьированием), значения магнитного поля Н и зна-

чения

начальной и конечной точек спектра относительно Н. Затем

указывается, какой из параметров необходимо варьировать, и шаг

его изменения. Рассчитанные спектры

«сбрасываются»

на диск и

выводятся на экран цветного графического дисплея цветом, отлич-

ным

от цвета предыдущего спектра. Это позволяет оперативно кон-

тролировать ход расчета и производить предварительное сравне-

ние

спектров.

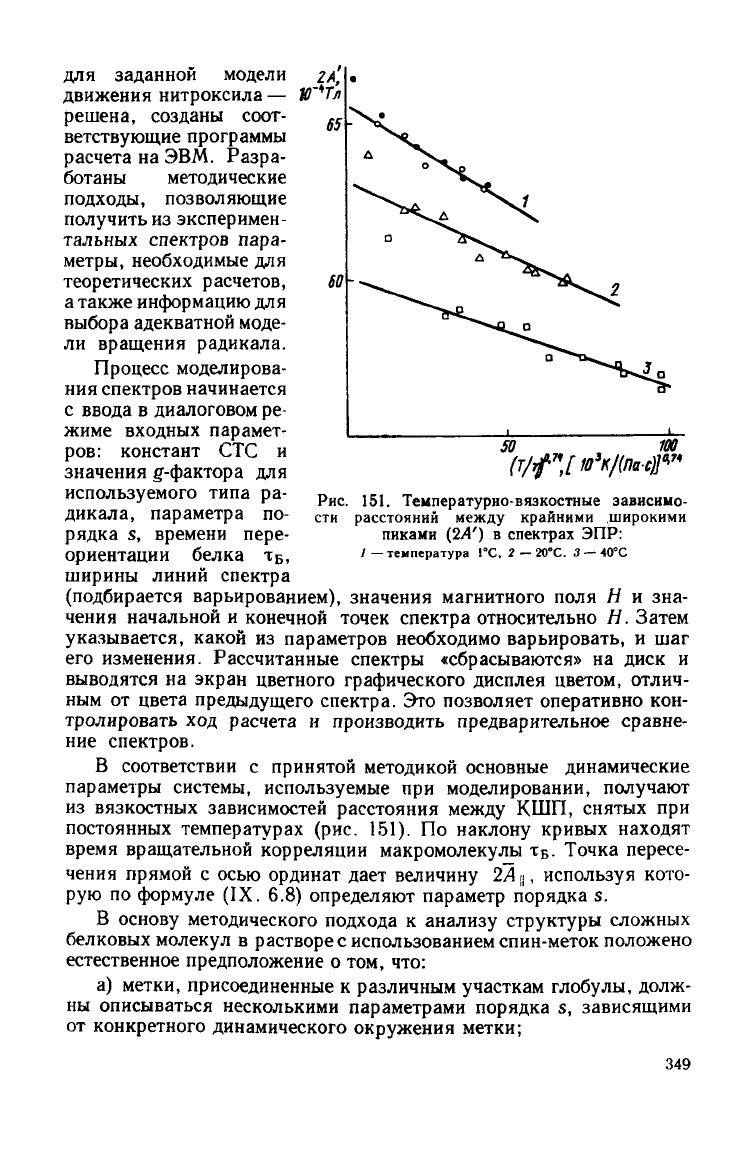
В соответствии с принятой методикой основные динамические

параметры системы, используемые при моделировании,

получают

из

вязкостных зависимостей расстояния

между

КШП, снятых при

постоянных

температурах

(рис. 151). По наклону кривых находят

время вращательной корреляции макромолекулы т

. Точка пересе-

чения

прямой с осью ординат

дает

величину 2А ц, используя кото-

рую по формуле (IX. 6.8) определяют параметр порядка s.

В основу методического

подхода

к анализу

структуры

сложных

белковых молекул в растворе с использованием спин-меток положено

естественное предположение о том, что:

а) метки, присоединенные к различным участкам глобулы, долж-

ны

описываться несколькими параметрами порядка s, зависящими

от конкретного динамического окружения метки;

Рис.

151. Температурно-вязкостные зависимо-

сти расстояний

между

крайними широкими

пиками

(2Л') в спектрах ЭПР:

/ —

температура

1°С. 2 —

20°С.

3 —

40°С

349

Рис.

152.

Модельные

экспериментальные спектры

ЭПР

спин-меченого

IgG

растворе

без

сахарозы

при

температуре

1°С:

— модельный спектр иммобилизованной метки вращения, 2 — модельный спектр

более

расторможенной

метки, 3 — суперпозиция спектров / и 2, 4 — спектр свободной метки

в растворе, 5 — суперпозиция модельных спектров I, 2 и 4, 6 — экспериментальный

спектр:

значения входных параметров, использованные при моделировании спектров,

указаны в тексте

б) если

глобула

состоит

из

нескольких частей, соединенных

гиб-

кими

связями,

то ее

динамическое поведение

будет

описываться

на-

бором времен вращательной переориентации белка

;

в)

при

изменении температуры

или

вязкости среды гибкая моле-

кула должна претерпевать значительные конформационные измене-

ния,

вследствие чего должны изменяться параметры

s и т

Экспериментальный

спектр, записанный

применением

про-

грамм управления спектрометром, приведен

на рис. 152, 6.

При

мо-

делировании использовали следующие входные параметры

=8;

= 6; А

37,25;

2,0093;

2,0061;

2,0022.

Ширина

линии

3,75-10~*

Тл.

Параметры

= 43 не и s = 0,78

определены

из

графиков, приведенных

на

рис.

151.

Спектр,

полученный

результате

моделирования, представлен

на

рис. 152, /. Его

сравнение

экспериментальным

(рис. 152, 6)

показывает,

что

последний отражает наличие дополнительного вкла-

да

от

более расторможенной метки

и от

свободной метки

растворе.

Определение значения

s для

более расторможенной метки произво-

дится

использованием

тех же

входных магнитных параметров

при

варьировании параметров

(один

из

спектров

для s = 0,47

приведен

на рис. 152, 2).

Варьированием весового вклада каждой

из

трех

составляющих добиваются совпадения суммарного модель-

ного спектра

(5) с

экспериментальным

(б).

Весь процесс анализа происходит

режиме общения исследова-

теля

системой посредством дисплея

соответствующего програм-

350