Рубин А.Б. Современные методы биофизических исследований (Практикум по биофизике)

Подождите немного. Документ загружается.

N,1N

2 N

Л/.

0,5

о о о о о

6 8 10

2 к 6 8 10

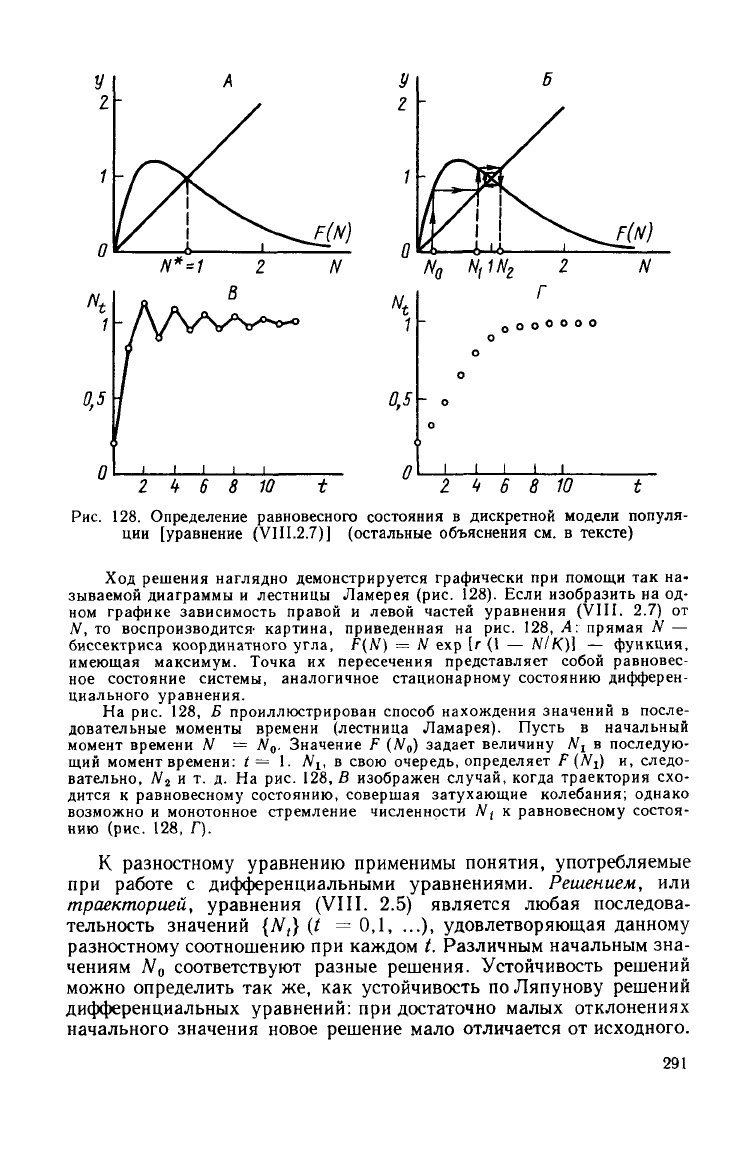
Рис.

128.

Определение равновесного состояния

дискретной модели популя-

ции

[уравнение (VIII.2.7)] (остальные объяснения

см. в

тексте)

Ход решения наглядно демонстрируется графически

при

помощи

так на-

зываемой диаграммы

лестницы Ламерея

(рис. 128).

Если изобразить

на од-

ном

графике зависимость правой

левой частей уравнения (VIII.

2.7) от

то

воспроизводится- картина, приведенная

на рис. 128, А:

прямая

N —

биссектриса координатного

угла,

F(N) = N ехр [г (1 — N1К)] —

функция,

имеющая максимум. Точка

их

пересечения представляет собой равновес-

ное

состояние системы, аналогичное стационарному состоянию дифферен-

циального уравнения.

На

рис. 128, Б

проиллюстрирован способ нахождения значений

после-

довательные моменты времени (лестница Ламарея). Пусть

начальный

момент времени

N — N

Значение

F (М

)

задает

величину

Л^ в

последую-

щий

момент времени:

/= 1. Л^, в

свою очередь, определяет

F (Л^) и,

следо-

вательно,

и т. д. На рис. 128, В

изображен случай, когда траектория

схо-

дится

равновесному состоянию, совершая

затухающие

колебания; однако

возможно

монотонное стремление численности

равновесному состоя-

нию

(рис. 128, Г).

разностному уравнению применимы понятия, употребляемые

при

работе с дифференциальными уравнениями.

Решением,

или

траекторией,

уравнения (VIII. 2.5) является любая последова-

тельность значений {JV,} (t = 0,1, ...), удовлетворяющая данному

разностному соотношению при каждом /. Различным начальным зна-

чениям JV

соответствуют разные решения. Устойчивость решений

можно определить так же, как устойчивость по Ляпунову решений

дифференциальных уравнений: при достаточно малых отклонениях

начального значения новое решение мало отличается от исходного.

291

Равновесием,

называется решение вида

const

= ./V*,

удовлетворяющее соотношению

F(N*). (VIII.2.8)

Если

решение (VIII.2.8) устойчиво,

его

называют

устойчивой

точ-

кой.

общем

случае

равновесие возможно, если уравнение

(VIII.2.8) имеет хотя

бы

один положительный корень

N*.

Как

и в

случае

дифференциального уравнения,

для

исследова-

ния

устойчивости равновесия применим линейный анализ. Положим

= N* + x

линеаризуем уравнение (VIII.2.5), разлагая

ряд по

степеням

— N* = x

отбрасывая члены порядка

х\

выше:

Из

условий сходимости геометрической прогрессии

следует

что

-у 0 при t-*- со,

если

\AFIAN\N>

< 1, и x

-*•

оо при t-*- со,

если

\dFldN\

, > 1. Эти

условия

определяют устойчивость

рав-

новесия

системы. Случаи

|d,F/djV|

= 1 и

dF/dN

— 0

требуют

дополнительного исследования членов более высокого порядка

разложении.

Можно

сделать некоторые заключения

характере приближе-

ния

(или

удаления) решений

от

равновесия:

случае

устойчивого

равновесия

при

0<(dF/d/V)

-.<

(VIII.2.9)

отклонения

от

равновесия исчезают монотонно.

Если

—

(dF/dW)*.

О,

(VII 1.2.10)

то имеют место затухающие колебания вокруг

JV*.

ЕСЛИ равновесие

неустойчивое,

то при

(dF/dN)

> 1

(VIII.2.11)

отклонение

от

равновесия монотонно растет,

а при

(dF/dN)

.< —

(VII 1.2.12)

удаление

от

равновесия происходит

виде нарастающих колебаний.

Для изучаемого уравнения (VIII.

2.7)

равновесие находят

из вы-

ражения

exp

[r(l

—

Очевидно,

что

единственное равновесное значение

N* = К > 0

существует

при

любом

г.

Условия (VIII.2.9), (VIII.2.10) показыва-

ют,

что

устойчивая точка имеет место, если

0 < г < 2, при

этом

-+N* монотонно

при 0< г < 1 и

колебательным образом

при

1 < г< 2.

Если

л<0 или г > 2, из

условий (VIII.2.11), (VIII.2.12)

сле-

дует,

что

равновесие неустойчиво.

292

Разностные уравнения

могут

иметь

более сложные решения,

например

в них

возможны циклы, являющиеся аналогами предель-

ных циклов для систем дифференциальных уравнений. Циклом дли-

ны

называется решение

{N'

}

уравнения (VIII.2.5), состоящее

из

конечного набора

значений, повторяющихся

строгой после-

довательности

(т. е. N't

--•••

+T>

£ = 0,l, 2, ...;

Ni+j^Nt,

= 1,2, ..., 7-1).

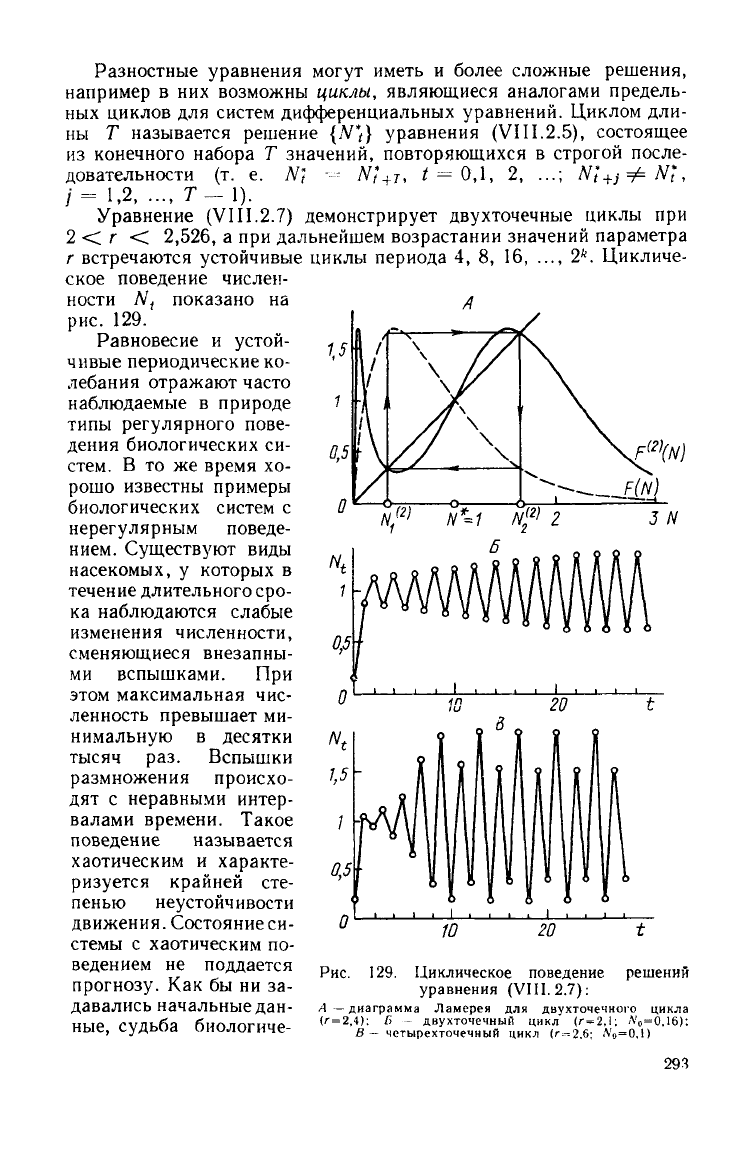
Уравнение

(VI11.2.7)

демонстрирует

двухточечные

циклы

при

2<r

2,526,

при дальнейшем возрастании значений параметра

г встречаются устойчивые циклы периода

4, 8, 16, ..., 2*.

Цикличе-

ское поведение числен-

ности

показано

на

рис.

129.

Равновесие

устой-

чивые периодические ко-

лебания отражают часто

наблюдаемые

природе

типы регулярного пове-

дения биологических си-

стем.

В то же

время

хо-

рошо известны примеры

биологических систем

нерегулярным поведе-

нием.

Существуют

виды

насекомых,

которых

течение длительного сро-

ка

наблюдаются слабые

изменения

численности,

сменяющиеся внезапны-

ми

вспышками.

При

этом максимальная

чис-

ленность превышает ми-

нимальную

десятки

тысяч

раз.

Вспышки

размножения происхо-

дят

неравными интер-

валами времени. Такое

поведение называется

хаотическим

характе-

ризуется крайней

сте-

пенью неустойчивости

движения. Состояние си-

стемы

хаотическим по-

ведением

не

поддается

прогнозу. Как

бы ни за-

давались начальные дан-

ные,

судьба

биологиче-

Рис.

129.

Циклическое

поведение

уравнения

(VIII.

2.7):

Л —диаграмма Ламсрея для двухточечного

( 2)Б i2l А'

решений

др

г = 2,4):

Б -

двухточечный

цикл

—

четырехточечный

цикл

(г

цикла

ir~2,l;

А'

=0.16):

2.6;

Л'

=0,1)

293

ской

популяции через

конечный

промежуток

времени практически не-

предсказуема.

Несмотря

на

кажу-

щуюся сложность хаоти-

ческой динамики,

она

может быть продемонст-

рирована

на

сравнитель-

но

простых разностных

моделях.

частности,

разностное уравнение

(VIII.2.7) наряду

с рав-

новесием

циклами

мо-

жет иметь хаотические

решения,

не

стремящие-

ся

ни

какому притяги-

вающему решению.

При

этом

существует

связь

между

наличием трехто-

чечных циклов и сущест-

вованием хаотических

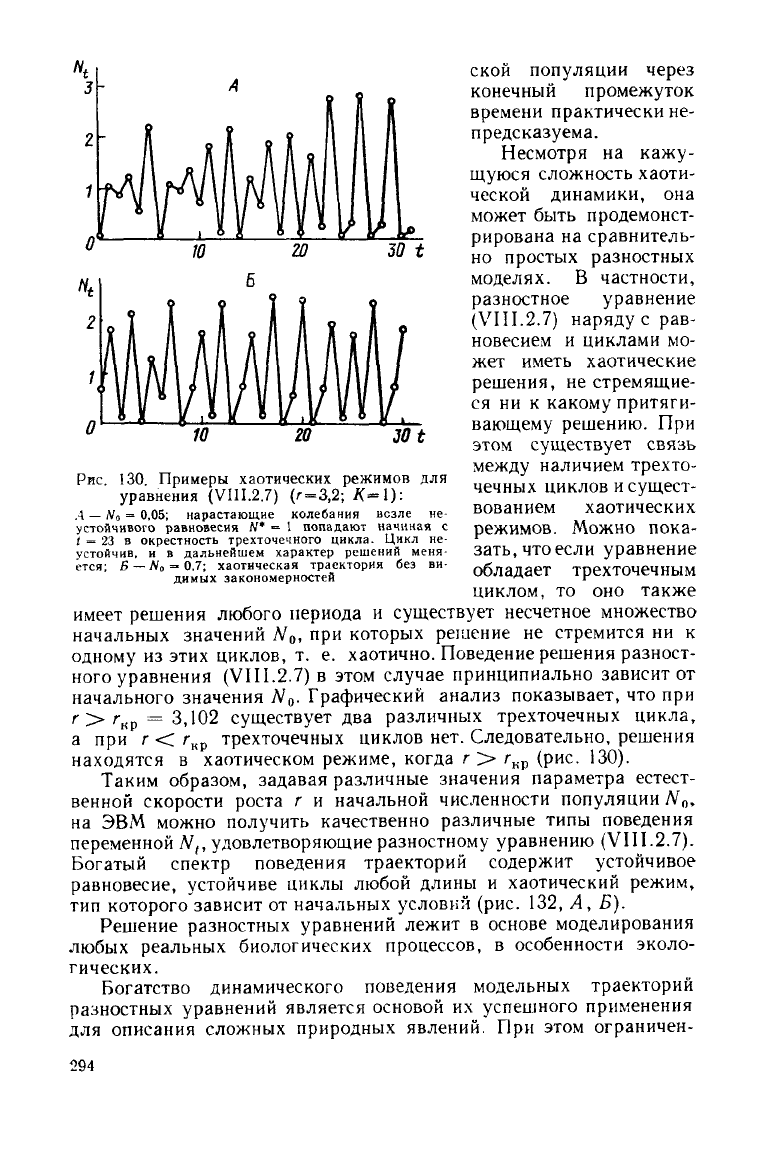
Рис.

130

Примеры хаотических режимов

для

уравнения (VIII.2.7) (г=3,2; К=1):

— Л/

= 0,05;

нарастающие

колебания

возле

не-

устойчивого

равновесия

Л"

попадают

начиная

реЖИМОВ.

МОЖНО

ПОКЭ-

— 23

окрестность

трехточечного

цикла.

Цикл

не-

устойчив,

и в

дальнейшем

характер

решений

меня-

ЗаТЬ,ЧТОеСЛИ

уравнение

ется;

Б—

N„

= 0,7;

хаотическая

траектория

без ви-

пбпяляРТ

ТПРХТОЧРЧНЫМ

димых

закономерностей

ооладае!

1рехшчечным

циклом,

то

оно

также

имеет решения любого периода

существует

несчетное множество

начальных значений

, при

которых решение

не

стремится

ни

одному

из

этих циклов,

т. е.

хаотично. Поведение решения разност-

ного уравнения (VIII.2.7)

этом

случае

принципиально зависит

от

начального значения JV

. Графический анализ показывает,

что

при

/•

3,102

существует

два

различных трехточечных цикла,

при

г <

кр

трехточечных циклов нет. Следовательно, решения

находятся

хаотическом режиме, когда

г >

кр

(рис.

130).

Таким

образом, задавая различные значения параметра естест-

венной

скорости роста

г и

начальной численности популяции JV

на

ЭВМ

можно получить качественно различные типы поведения

переменной

N,,

удовлетворяющие разностному уравнению (VIII.2.7).

Богатый спектр поведения траекторий содержит устойчивое

равновесие, устойчиве циклы любой длины

хаотический режим,

тип которого зависит

от

начальных условий (рис. 132,

А,

Б).

Решение разностных уравнений лежит

основе моделирования

любых реальных биологических процессов,

особенности эколо-

гических.

Богатство динамического поведения модельных траекторий

разностных уравнений является основой

их

успешного применения

для описания сложных природных явлений.

При

этом ограничен-

294

ность параметрических областей существования определенного типа

решений может служить дополнительным основанием

для

оценки

адекватности предлагаемой модели.

Примерное построение учебной задачи

1. Написать программу

для

ЭВМ

для

решения (VIII.2.7)

получить

на

ЭВМ численность

зависимости

от

времени

при

различных значениях

Л'

и г,

соответствующих трем различным типам динамического поведения

модели: устойчивому равновесию, устойчивым циклам

хаотическому

по-

ведению системы.

2. Написать программу

для ЭВМ

решения непрерывного уравнения

(VIII.2.3), получить динамику численности

х (/) на

этой модели

при тех же

значениях параметров

сравнить решения, полученные

для

дифференциаль-

ного (VIII.

2.3)

разностного (VIII.2.7) уравнений. Результаты представить

виде графиков.

Для

решения может быть использован численный метод

Рун-

ге

—

Кутта.

Модель

переноса электрона в фотосинтетической

электрон-транспортной цепи. Выяснение типа взаимодействия

переносчиков

Процессы трансформации энергии

при

фотосинтезе включают

себя

качестве необходимого элемента перенос электронов

между

встро-

енными

мембрану окислительно-восстановительными фермента-

ми,

образующими электрон-транспортную цепь

(ЭТЦ).

результате

переноса электрона

по ЭТЦ и

дальнейших превращений энергия

света запасается

виде энергии макроергических связей

АТФ.

Модель фотосинтетической

ЭТЦ в

терминах современной теории

управления может быть записана

следующем

виде:

dx,

F (х, и); x(t = t

) = x

;

= i)(x) + v (t),

где

х —

Л'

-мерный вектор, характеризующий состояние пере-

носчиков

электронов

в ЭТЦ; t —

время;

v, у —

Л^-мерный

Л^-мерный векторы управления

(входа)

наблюдения

(вы-

хода). Компоненты вектора наблюдений

являются функциями

переменных системы

х и

могут

также испытывать влияние шумов

измерений

искажающих

результаты

наблюдения

за

системой;

т|

(х) = Н

, Н —

матрица коэффициентов размерности

х N

(t) —

Л^.-мерный вектор шумов измерений;

F —

оператор пере-

ходов.

При

построении модели оператора

исходят

из

имеющихся пред-

ставлений

механизмах переноса электронов

между

компонентами

ЭТЦ.

Процесс представляет собой последовательность окислитель-

но-восстановительных реакций

между

локализованными

фотосин-

тетической мембране молекулами, организованными

комплексы,

может быть описан системой линейных дифференциальных урав-

нений

для

вероятностей состояний этих комплексов. Возможно

так-

295

же бимолекулярное взаимодействие компонентов фотосинтетиче-

ских комплексов с подвижными в мембране или среде окислитель-

но-восстановительными агентами; этот процесс может быть описан

с помощью закона действующих масс. Например, подвижные в фо-

тосинтетической мембране переносчики — пластохиноны — осуще-

ствляют сопряженный с переносом протонов перенос электронов

между

второй и первой фотосистемами зеленых растений.

При

построении математической модели ЭТЦ конкретного фото-

синтезирующего объекта необходимо знать тип взаимодействия пере-

носчиков на том или ином участке цепи. В математической формули-

ровке вопрос сводится к выяснению формы оператора F, характе-

ризующего связь

между

переменными системы и управляющими

воздействиями. Решить вопрос о природе взаимодействия перенос-

чиков помогает сравнение свойств альтернативных моделей (в соот-

ветствии со схемой VIII. 1.2). На первом этапе исследования можно

считать, что наблюдаемые отклики системы на управляющие воз-

действия (в данном

случае

включение и выключение света) не иска-

жены шумами.

Рассмотрим два типа описания переноса электрона: при помощи

закона

действующих масс, пригодное для окислительно-восстано-

вительных реакций в растворе, вероятностное — для переноса

электрона в мультиферментном комплексе.

Применение

закона действующих масс основано на предполо-

жении о том, что вероятность протекания реакции (в разбираемом

случае

— окислительно-восстановительной) определяется вероят-

ностями нахождения каждого из реагентов в реакционноспособном

состоянии.

Например,

для реакции переноса электрона

между

двумя под-

вижными переносчиками С

и С

, взаимодействующими по

схеме

D^C^C^A,

(VII

1.3.1)

кинетические уравнения

могут

быть записаны в виде

d [СЦ/d/ = k[ ID

] [C\] — k'

[С\][С°,

°,У,

Здесь ID

], [C\], [Cl] — концентрации восстановленной фор-

мы экзогенного донора D и переносчиков электронов С

и С

; 1С'],

1С?].

[А

] — концентрации окисленной формы переносчиков С

и экзогенного акцептора A; k[, k'

, £3 — бимолекулярные кон-

станты скорости соответствующих реакций.

В дальнейшем

будем

считать, что концентрация соответствую-

щих форм экзогенных доноров и акцепторов поддерживается посто-

янной

на всем рассматриваемом промежутке времени и что общие

концентрации

переносчиков [С

] и [С

] равны. Предположим, что

каждый переносчик может находиться только в одном из

двух

со-

296

стояний:

окисленном (верхний индекс — 0) или восстановленном

(верхний индекс — 1):

Эти

предположения

позволяют

записать

систему

дифференциаль-

ных

уравнений

для

относительных

концентраций

соответствующих

переносчиков

восстановленной

форме:

dyjdt

= k

(I — у

)—

(1 — у),

/dt

(i-y

)-k

y2.

(VIII.3.1а)

Здесь

У1

= 1СШС

]; У* = [С

]/[С

];

kj, = k[ ID

]; *

= *2

];

= & U«].

Система уравнений для цепи из п компонентов содержит п нели-

нейных уравнений. Для случая п • •-- 1,2, 3 стационарное решение

можно найти аналитически. Для нахождения стационарного реше-

ния

при /i>3 и определения поведения переменных во времени

при

п > 2 требуется ЭВМ.

2. Фотосинтетический реакционный центр (РЦ) представляет со-

бой молекулярную машину, которая «включается» квантом света.

РЦ

представляет собой фиксированный в мембране мультифермент-

ный

комплекс, редокс-состояния компонентов которого не являются

независимыми

друг

от

друга.

Рассмотрим принципы математического описания переноса элек-

трона в комплексах

молекул-переносчиков,

внутри которых задана

строгая последовательность взаимодействия переносчиков электро-

на

друг

с другом. Пусть

существует

пара переносчиков С

и С

, объ-

единенных в комплекс:

(VIII.3.2)

Перенос

электрона от С, к С

в рассматриваемом

случае

явля-

ется мономолекулярным процессом, поскольку в едином акте про-

текают как окисление Q, так и восстановление С

. В силу этого пе-

ренос электрона

между

Cj и С

не происходит, когда оба переносчи-

ка,

входящие в комплекс, одновременно или окислены, или восста-

новлены.

Поэтому для описания переноса электрона в таких комп-

лексах

следует

рассматривать состояния сразу

двух

переносчиков,

участвующих в переносе электрона. Скорость переноса электрона

между

С, и С

в рассматриваемом

случае

пропорциональна концент-

рации

комплексов, находящихся в состоянии ICiC'l, когда перенос-

чик

восстановлен, а переносчик С

окислен. Тогда скорость пере-

носа электронов

между

и С

равна v —- k

IC2C2L

В общем

случае

для описания переноса электронов в комплексе

необходимо рассматривать все состояния, в которых может нахо-

297

диться комплекс.

При

этом каждый

из

переносчиков, входящих

комплекс,

может находиться

окисленной

или

восстановленной

форме,

протонированном

или

депротонированном состоянии

и пр.

Обозначим состояния комплекса через

, ..., S

введем

вероятность того,

что

комплекс переносчиков находится

состоя-

нии

S; в

момент времени

t.pi (S

, t) = p

(t).

События

, ...,

несовместны

образуют полную группу событий, поэтому

вы-

полняется равенство (условие нормировки)

2>(S,,

0 = 1.

Будем рассматривать переходы

между

состояниями

комплек-

са

как

марковский процесс

конечным числом состояний

непре-

рывным временем.

этом

случае

переходы комплекса

из

одного

со-

стояния

другое

описываются системой линейных дифференциаль-

ных уравнений относительно вероятностей

dpi,/dt=--

/= 1

Mi=l

я),

(VII

1.3.3)

или

векторном виде dp/df

- К

р\ р (0) - Ь.

Здесь вектор

р --•

—

{р

(t), ..., р

(/)); pi (t) —

вероятность того,

что

комплекс пере-

носчиков находится

в г-м

состоянии

момент

/, К* —

матрица,

транспонированная

матрице

К —

(kij), элементы которой

kjj

(i Ф ])

суть

константы скоростей перехода

из t-го

состояния

ком-

плекса

в /-е,

причем

= 2

-; b = (b

, ... , b

) —

вектор вероятно-

стей начальных состояний комплекса.

Общий

вид

решения системы

(VII 1.3.3)

может быть записан

виде

= ехр (К

Ь.

При

рассмотрении конкретных

ЭТЦ

удобно представлять состо-

яния

комплекса

виде размеченного графа,

вершинах которого

стоят состояния комплекса,

стрелки указывают возможные пере-

ходы

между

состояниями.

частности,

для

переноса электрона

комплексе

из

двух

переносчиков (VIII.3.2) размеченный граф

со-

стояний

будет

иметь следующий

вид:

(VIII.

3.4)

298

Здесь верхние индексы 0 и 1 означают

отсутствие

и наличие элект-

рона на соответствующем переносчике; цифры в скобках указыва-

ют номер состояния комплекса; k

— константы скоростей соот-

ветствующих

переходов. В общем

случае

константы скоростей пере-

ходов

между

состояниями комплекса

могут

зависеть от состояний

переносчиков, не принимающих непосредственно участия в реакции

(эффект

кооперативности).

Параметры а и Р характеризуют сте-

пень

кооперативности. Например, скорость притока электронов от

внешнего донора на переносчик С

может быть различной в зависи-

мости от окислительно-восстановительного состояния переносчика

(аф

1).

Система дифференциальных уравнений для вероятностей состоя-

ний

комплекса

описывающая его функционирование, согласно

(VIII.3.4) при а — р = 1 имеет вид

dpjdt

= k

— ft! p{,

dpjdt

= k

—(k

-f k

) p

;

/dt

= k

+ k

—k

;

dp/dt

-•=

p,—k

Решив

систему уравнений (VIII.3.5) относительно вероятностей

состояний

комплекса p

, легко найти и вероятности состояний от-

дельных переносчиков, просуммировав вероятности

всех

тех состоя-

ний

комплекса, которые содержат рассматриваемый переносчик в

интересующем нас состоянии. Например, вероятность того, что пер-

вый переносчик находится в окисленном состоянии, равна

сумме

ве-

роятностей первого и второго состояний [см. (VIII.3.4)]:

р (С°) = р(С\ С»)

+р(СЧ)

1-р(С\).

В общем виде

р{С„ t) - ^ P(

O- 0; р(С\. « = i-/>(C?, t),

или

р(В) =--2 p(S

t),

где суммирование производится по всем тем элементарным событи-

ям

, которые составляют событие В.

Для большого числа одинаковых, не взаимодействующих меж-

ду собой комплексов переносчиков введенные выше вероятности

р (S

, t) и р (С°, i), согласно закону больших чисел, приближенно

равны соответственно

доле

комплексов, находящихся в состоянии

доле

молекул-переносчиков С,, которые находятся в соответ-

ствующем состоянии.

Сравнение

двух

типов описаний. Несмотря на то что вероятност-

ное описание переноса электрона в комплексах и описание окисли-

тельно-восстановительных реакций в растворе при помощи закона

299

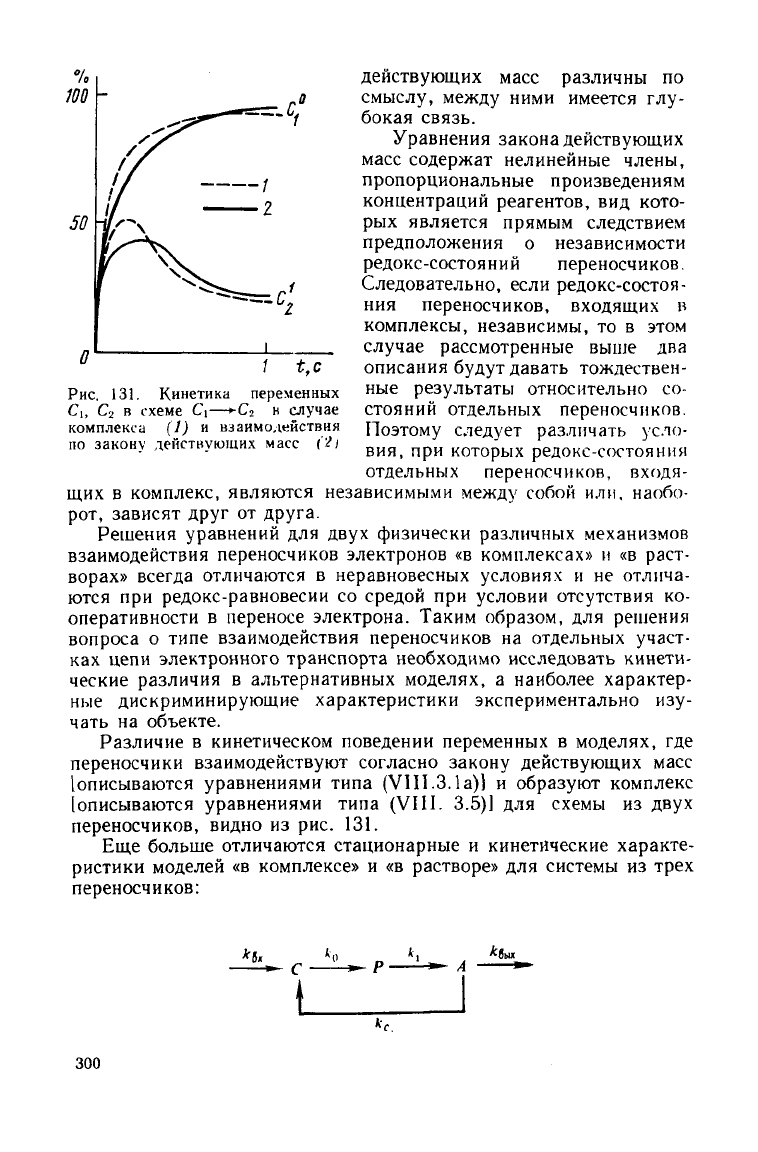
Рис.

131. Кинетика переменных

схеме

С\—<-С

случае

комплекса (1) и взаимодействия

по

закону действующих масс Ch

действующих масс различны по

смыслу,

между

ними имеется глу-

бокая

связь.

Уравнения закона действующих

масс содержат нелинейные члены,

пропорциональные произведениям

концентраций

реагентов, вид кото-

рых является прямым следствием

предположения о независимости

редокс-состояний переносчиков.

Следовательно, если редокс-состоя-

ния

переносчиков, входящих в

комплексы,

независимы, то в этом

случае

рассмотренные выше два

описания

будут

давать тождествен-

ные результаты относительно со-

стояний

отдельных переносчиков.

Поэтому

следует

различать усло-

вия,

при которых редокс-состояния

отдельных переносчиков, входя-

щих в комплекс, являются независимыми

между

собой или, наобо-

рот, зависят

друг

от

друга.

Решения

уравнений для

двух

физически различных механизмов

взаимодействия переносчиков электронов «в комплексах» и «в раст-

ворах»

всегда отличаются в неравновесных условиях и не отлича-

ются при редокс-равновесии со средой при условии отсутствия ко-

оперативности в переносе электрона. Таким образом, для решения

вопроса о типе взаимодействия переносчиков на отдельных

участ-

ках цепи электронного транспорта необходимо исследовать кинети-

ческие различия в альтернативных моделях, а наиболее характер-

ные дискриминирующие характеристики экспериментально изу-

чать на объекте.

Различие в кинетическом поведении переменных в моделях, где

переносчики взаимодействуют согласно закону действующих масс

1описываются уравнениями типа (VI

11.3.1а)]

и образуют комплекс

[описываются уравнениями типа (VIII. 3.5)1 для схемы из

двух

переносчиков, видно из рис. 131.

Еще больше отличаются стационарные и кинетические характе-

ристики

моделей «в комплексе» и «в растворе» для системы из

трех

переносчиков:

300