Рубин А.Б. Современные методы биофизических исследований (Практикум по биофизике)

Подождите немного. Документ загружается.

шое количество методов поиска экстремума. Удобным методом для

нахождения минимума функции S является

метод

сопряженных

гра-

диентов.

Суть его состоит в следующем. Пусть необходимо найти

минимум функции / (х), зависящей от нескольких переменных х.

Выберем в качестве начальной точку х<

. Вычислим в этой точке

v/ (x

>). В качестве следующей точки возьмем

(i)

—х<°)

-fA.*

<0>

(0)-

(0)

= \7/(х

<0)

(VII.4.5)

Число

Л.*<°>

находят из требования, чтобы функция / (х) имела в на-

правлении, определяемом вектором S

<0)

, минимум (предполагают,

что он достигается при X —

А.*

т. е. х = х

(1)

. После этого вычисля-

ют

следующую

величину:

—; V

/(</)v/(</) = S(|")

(VH.4.6)

где k — число переменных функций /, по которым производится

минимизация.

С помощью ш

находят новое направление поиска:

§(i)

=_-

у/(х

(|)

)

-f S

(0)

o)j.

(VII.4.7)

Проводят поиск минимума в направлении S

(1)

. определяют точку

х<

> и т. д. Рекуррентное соотношение для метода сопряженных

градиентов следующее:

(VII.4.8)

После (k + 1)-итерации эта процедура циклически повторяется

с заменой х

(0)

на

(

+1)

Поиск минимума прекращается при вы-

полнении

условия У (S)

< е, где е много меньше единицы. Одно-

мерный поиск минимума функции / (х) в каком-либо направлении

5 удобно проводить методом кубической интерполяции.

Пусть

требуется

определить минимум функции ф (х), зависящей

от одной переменной х. Для этой функции известны ее значения на

концах некоторого отрезка [а, Ь] — ф (а) и ф (Ь), первые производ-

ные в точках а и Ь: ф' (а) и ф' (Ь) [для определенности положим

ф'

(а) < о. ф' (р) >01. Тогда на этом отрезке функцию ф (х) можно

аппроксимировать кубической параболой, имеющей минимум в точке:

••=

\/'z

~(f'

(а)ф' (b). (VI

1.4.9)

2SI

Если |ф' (*)| <С е

, где е

— малое число, то поиск корня прекра-

щается, в противном

случае

точка х становится одним из краев от-

резка, внутри которого ищется минимум, и вычисления (VII. 4.9)

повторяются.

Использование метода сопряженных градиентов для нахожде-

ния

набора параметров, минимизирующих функцию S, удобно по

двум

причинам: достаточно просто вычислить первые производные

функции

S по параметрам {а;}, и этот метод быстро сходится, т. е.

минимум функции S определяется после не очень большого числа

итераций (VII. 4.8).

Задача нахождения минимума функции S по изложенному выше

алгоритму может выполняться на ЭВМ. На кафедре биофизики

Биологического факультета МГУ созданы программы, решающие

поставленную

задачу

путем

разложения экспериментального мёсс-

бауэровского спектра на две функции Лоренца с последующим оп-

ределением фактора Лэмба — Мёссбауэра и подгонки экспери-

ментального спектра функцией броуновского осциллятора с целью

определения параметров х

и т

(

. Эти программы написаны на языке

ФОРТРАН-IV, адаптированы для операционных систем ОС РВ и

RSX и используются при обработке экспериментальных спектров.

Глава

VIII

Математическое моделирование

1. Общие принципы построения моделей биологических

явлений

Современная

биологическая наука характеризуется высоким уров-

нем

математизации на

всех

уровнях, начиная от обработки данных

наблюдений и экспериментов и кончая построением функциональ-

ных математических моделей изучаемых процессов и явлений в жи-

вой

природе.

Биологические

системы, по сути, являются чрезвычайно слож-

ными

структурно-функциональными единицами. Для того чтобы ус-

тановить закономерности их функционирования, необходимо вы-

брать правильный уровень общности их рассмотрения, чтобы, не

«увязая»

деталях,

понять и формализовать основные и важные для

естественно-научных и практических целей свойства биологических

систем. Применительно к исследованию биологических объектов

системный

подход

подразумевает последовательность действий, изоб-

раженную на

схеме

VIII. 1.1.

Изучая

биологическое явление, исследователь переходит к пос-

троению его математической модели, выявляет формальные свойства

этой

модели, а затем интерпретирует выводы исследования на мате-

риалах наблюдения или эксперимента. Таков общий ход работы над

математической моделью биологической системы.

Чаще

всего модели биологических процессов задаются в виде

дифференциальных

или разностных уравнений, но возможны и дру-

гие типы представлений модели, такие, как некоторые нечисленные

процедуры, алгоритмы или модели в виде программ для вычисли-

тельной машины. После того как модель построена, задача сводится

283

Схема

VIII.1.1.

Системный

подход

моделировании биологического объекта

Формальная система

(модель)

Исследование модели

(дедукция)

Системные свойства

(свойства модели)

Моделирование

(абстрагирование)

нтерпре гация

Биологическое явление

Биологические характеристики

изучению ее свойств методами математической дедукции или пу-

тем машинного моделирования.

Выбор математического аппарата для модели определяют не

только экспериментальными условиями и свойствами биологиче-

ского объекта, но и наличием математических результатов, которы-

ми

можно воспользоваться при рассмотрении тех или иных свойств

объекта. Например, если исследуют устойчивость, то удобно за-

дать модель системы в виде дифференциальных или разностных урав-

нений.

Если изучают проблемы декомпозиции и нахождения под-

систем, предпочтительными

могут

оказаться некоторые алгебраи-

ческие модели. Когда система может находиться в нескольких ди-

скретных состояниях, способных переходить

друг

друга,

удобно

изобразить эти состояния в виде графа, а переходы

между

ними опи-

сывать при помощи вероятностной теории марковских процессов.

В любом

случае

задачей исследования является отыскание связи

между

измеряемыми переменными.

При

изучении закономерностей биологического явления обыч-

но

предлагают несколько альтернативных моделей. Проверяют

качественное

соответствие этих моделей объекту. Например,

уста-

навливают наличие устойчивых стационарных состояний в моде-

ли,

существование колебательных или триггерных режимов. Мо-

дель, наилучшим образом соответствующую исследуемой биологи-

ческой системе, выбирают в качестве

базовой.

Затем выбранную мо-

дель уточняют применительно к конкретной исследуемой системе и

проводят идентификацию параметров этой модели, т. е. определе-

ние

числовых значений параметров по экспериментальным данным

(схема VIII. 1.2).

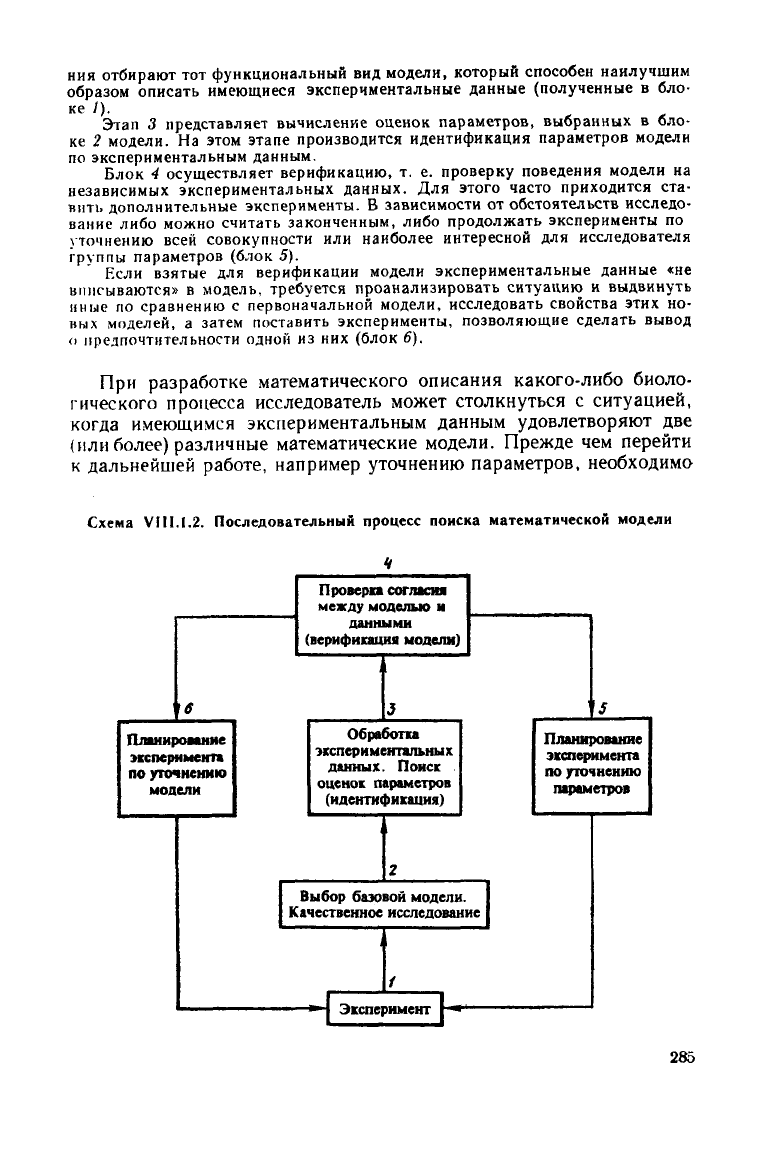
Блок

соответствует

имеющимся

началу исследования данным

об изу-

чаемом объекте

или

проведению некоторого затравочного эксперимента,

ко-

торый позволяет получить

«грубую»

информацию

процессе.

В блоке

осуществляется выбор базовой модели

из

возможных альтер-

нативных моделей

по

качественным признакам.

Для

дальнейшего исследова-

284

ния

отбирают

тот

функциональный

вид

модели, который способен наилучшим

образом описать имеющиеся экспериментальные данные (полученные

в бло-

ке

/).

Этап

представляет вычисление оценок параметров, выбранных

в бло-

ке

модели.

На

этом этапе производится идентификация параметров модели

по

экспериментальным данным.

Блок

осуществляет верификацию,

т. е.

проверку поведения модели

на

независимых экспериментальных данных.

Для

этого часто приходится

ста-

вить дополнительные эксперименты.

зависимости

от

обстоятельств исследо-

вание либо можно считать законченным, либо продолжать эксперименты

по

уточнению всей совокупности

или

наиболее интересной

для

исследователя

группы параметров (блок

5).

Если взятые

для

верификации модели экспериментальные данные

«не

вписываются»

модель, требуется проанализировать ситуацию

выдвинуть

иные

по

сравнению

первоначальной модели, исследовать свойства этих

но-

вых моделей,

затем поставить эксперименты, позволяющие сделать вывод

предпочтительности одной

из них

(блок

6).

При

разработке математического описания какого-либо биоло-

гического процесса исследователь может столкнуться с ситуацией,

когда имеющимся экспериментальным данным удовлетворяют две

(или

более) различные математические модели. Прежде чем перейти

дальнейшей работе, например уточнению параметров, необходимо

Схема

VI11.1.2.

Последовательный процесс поиска математической модели

Планирование

эксперимента

по уточнению

модели

Проверка согласия

между

моделью

данными

(верификация модели)

Обработка

экспериментальных

данных.

Поиск

оценок параметров

(идентификация)

Выбор базовой модели.

Качественное исследование

•4

Эксперимент

Планирование

эксперимента

по уточнению

параметров

286

сделать выбор

между

этими моделями. Для того чтобы поставить

дискриминирующий эксперимент, необходимо исследовать модели и

найти

такие их свойства, которые бы отличались для

двух

моделей.

Если речь идет о регистрации кинетических кривых, нужно найти

такие точки, результаты измерений в которых не были бы инвари-

антны

относительно замены одной проверяемой модели на

другую,

например химическая реакция, в которой вещество А используется

для получения продукта В. Пусть реакция может быть одного из

двух

видов с обратимой или необратимой последней стадией:

Мод ел ь I А >- В

>•

Модель 2 А • В~ * С

Типичные

кривые, показывающие зависимость концентрации

продукта как функции времени, показаны на рис. 125. Ясно, что,

для того чтобы выявить, какая из моделей верна, бессмысленно про-

изводить измерения в области / < 10 мин, необходимы большие

времена. Однако при слишком больших временах работать бывает

экономически

невыгодно, поэтому необходим поиск компромиссного

решения;

в данном

случае

пригодно / ~ 100 мин.

Процесс

поиска адекватной модели не может быть полностью

формализован.

На

всех

этапах, в особенности на этапе выбора аль-

тернативной модели и постановки дискриминирующего эксперимен-

та,

успех

исследования во многом зависит от опыта и интуиции спе-

циалиста и каждая научная проблема решается по-своему. Однако

два момента в сложном пути исследования, изображенном на схе-

ме VIII.1.2, имеют сейчас достаточно развитый формальный мате-

матический аппарат, который необходимо научиться применять, что-

бы успешно решать

задачу

математического моделирования биоло-

гических систем.

Качественная

теория

дифференциальных и разностных урав-

нений,

позволяющая установить качественные черты поведения

предлагаемых моделей: возможность ус-

тойчивых стационарных состояний, ко-

лебательных, триггерных и квазисто-

0,1*

0.2

хастических режимов, бифуркационные

свойства модели в различных областях

параметров и пр. Этой теорией необхо-

димо владеть при выборе альтернатив-

/ 2 h 8

32 64

128

них моделей. В качестве примера при-

Время,

логарифмическая

шкала

менения качественных методов может

быть выбрана любая модель биологиче-

Рис.

125. Концентрация про. ского процесса, сводимая к системе из

дукта

В как функция вре-

одного или двух

дифференциальных

мени

для механизма реак- - и ,

«•

о X » \

ции

А vS —с (/) и ме уравнении. Ниже (см. § 2, 3 этой главы)

ханизма А^в*±с (2) разобраны два примера: модель роста

286

биологической популяции

ограниченной среде

математическая

модель переноса электрона

фотосинтетической электрон-транс-

портной

цепи

(ЭТЦ).

Теория

идентификации

параметров динамических систем,

применение

методов которой позволяет

во

многих случаях доста-

точно точно (иногда однозначно) оценить числовые значения пара-

метров предлагаемых моделей.

Рост

биологической популяции в условиях ограниченности

ресурсов.

Непрерывное и дискретное описание

Основным свойством живых организмов является

их

способность

росту

размножению. Большинство моделей биологических

про-

цессов самого разного уровня сложности содержит описание дина-

мики

популяций (популяций клеток

— на

уровне организмов

и тка-

ней,

популяций растений

или

животных

— на

экологическом уров-

не).Здесь рассмотрены методы качественного

машинного исследова-

ния

непрерывной

дискретной моделей популяции

ограниченной

среде.

Уравнение, описывающее динамику численности популяции,

можно записать

общем виде:

x=--F(x),

или x =

xf(x).

(V1II.2.1)

Изменение

численности складывается

из

двух

процессов:

раз-

множения

гибели особей. Если

их

рассматривать порознь, урав-

нение

(VIII.

2.1)

приобретает

вид х — В (х) —D (х) или х =

х \Ь (х) —

d(x)\. Здесь

В(х) и D (х) —

абсолютные скорости

рождения

гибели особей,

b (х) и d (x) —

соответствующие

удель-

ные скорости, отнесенные

общей численности популяции (плодо-

витость

смертность). Если плодовитость

смертность

не

зависят

от численности популяции,

что

наблюдается, например,

при

разм-

ножении

путем деления, получают уравнение экспоненциального

роста популяции:

x =

(b—d)x=ax.

(VII 1.2.2)

Динамика

численности такой популяции представлена

на рис. 126

(кривые

/).

Очевидно,

что

беспредельный рост популяций, описан-

ный

выше, невозможен из-за ограниченности внешних ресурсов

популяции:

источников пищи, мест обитания

и т. п.

Ограничен-

ность внешних ресурсов приводит

внутривидовой конкуренции,

вследствие которой плодовитость

ростом плотности популяции

падает,

смертность возрастает. Наиболее простым

подтвержден-

ным

во

многих случаях экспериментально является предположение

линейном

характере этих зависимостей. Обозначая через

(х)

(x)

зависимость плодовитости

смертности

от

плотности

в сво-

287

Рис.

126.

Динамика численности

популяции

для

моделей экспонен-

циального

(1) и

логарифмического

(2)

роста.

А —

зависимость

чис-

ленности

от

времени;

Б —

зависи-

мость скорости роста

от

числен-

ности

бодной популяции, а теми же буквами без индекса — аналогичные

величины в ограниченной ресурсами популяции, можно записать:

b (х) = b

(х) — 1

(*); d (х) = d

(х) —l

Здесь /,,

i(i

— коэффициенты пропорциональности, характеризую-

щие влияние конкуренции на плодовитость и смертность. Общее

уравнение динамики численности с

учетом

внутривидовой конку-

ренции

принимает вид

= х [Ь

(х) - d

(х) - lx\ = В

(х) — D

(х) - 1х

= F

(x) - 1х\

Учет

ограниченности ресурсов превращает уравнение (VIII. 2.2) в

известное логистическое уравнение Ферхюльста — Пирла:

или

гх(\—х/К)', г — аК,

(VIII 23)

где г — скорость роста популяции в

отсутствие

ограничений.

Динамика численности в этом

случае

представлена на рис. 126 кри-

выми 2. При любом исходном состоянии популяции ее численность

монотонно

стремится к значению К,. Таким образом, К представ-

ляет собой максимально возможную численность популяции. Если

исходная численность меньше Л72, то кривая зависимости числен-

ности от времени имеет на высоте К-'2 перегиб.

Рассмотрим свойства стационарных состояний уравнения

(VIII. 2.3), пользуясь методами качественной теории дифференциаль-

ных уравнений. В стационарном состоянии х

йх/dt

-О; в описываемом

случае

уравнение стационарных состояний (гх (1 — х~К) — 0 име-

ет два корня: х

= 0, х

•—

К- Для исследования устойчивости

решений

воспользуемся аналитическим методом Ляпунова.

Введем

новую переменную £, обозначающую отклонение переменной х от ее

стационарного значения: I -•- х —х. Запишем линеаризованное

уравнение для нелинейного уравнения (VIII.2.3): dl'd/ a\,

где а =- f (jc)|

,..i.

Знак

величины a {x

) определяет устойчивость соответствующей

особой точки x

•=

1,2):

~(2«;/C).

(VI

11.2.4)

288

Подставив

выражение (VIII.2.4) значение первого корня

=0,

получим

a (Xj) = г. Эта

величина

всегда

положительна,

так как,

по

определению,

г —

коэффициент естественной скорости роста

популяции

(г —

величина положительная). Следовательно,

0 —

неустойчивая особая точка. Если подставить

выражение

(VIII.2.4)

= К, то а (х

) = — г, т. е. г

становится отрица-

тельной величиной; следовательно, стационарное решение уравне-

ния

(VIII.2.3)

= К

является устойчивым

соответствует

устой-

чивому стационарному режиму существования популяции

ограни-

ченной

среде.

Проведем теперь исследование устойчивости стационарных реше-

ний

уравнения (VIII.2.3), исходя

из

графика функции

(JC)

d x/dt. Из рис. 126, А

(кривая

видно,

что при

переходе

от от-

рицательных

положительнм значениям

х в

точке

= 0

функция

(х)

меняет

знак

минуса

на

плюс,

т. е.

особая точка является

не-

устойчивой. Наоборот,

точке

= К

знак

/ (х) с

ростом

меняет-

ся

плюса

на

минус; следовательно,

эта

особая точка

—

устойчивая.

Таким

образом, качественное исследование дифференциального

уравнения (VIII.2.3)

для

численности популяции

ограниченной

среде

показывает монотонное стремление численности

определен-

ной

максимальной величине

К-

Уравнение (VIII.2.3) хорошо

опи-

сывает некоторые реальные процессы, например процесс размноже-

ния

пенициллиновых грибков

культуральной среде.

Если

же

численность популяции

ведет

себя по-иному, например

колеблется

или

меняется хаотически, необходимо обратиться

к дру-

гому

математическому аппарату

для

описания процесса. Одна

из

возможностей

—

учет

взаимодействия изучаемой популяции

с дру-

гими

—

требует

введения

модель новых переменных

соответст-

венно

дополнительных уранений.

Другая

—

переход

разност-

ным

уравнениям

—

разобрана ниже.

Разностное

уравнение для численности популяции

в ограниченной

среде

Описание динамики численности

при

помощи уравнения типа

(VIII.2.1); (VIII.2.2); (VIII.2.3) предполагает некоторые допущения.

Для того чтобы численность популяции можно было аппроксими-

ровать непрерывной кривой,

она

должна быть достаточно многочис-

ленной.

Запись закона изменения переменной

виде обыкновенных

дифференциальных уравнений предполагает,

что

изменение числен-

ности

каждый момент времени

зависит лишь

от

мгновенного

ее

значения

данный момент времени.

Более

соответствует

реальности представление

численности

как

дискретной величине

которая принимает некоторые значения

фиксированные

моменты времени.

Это в

точности отражает процесс

289

переписи

реальных (лабораторных

или

естественных) популяций.

Если

при этом также

учесть,

что численность

зависит

от

числен-

ности

предшествующие моменты времени, возникает необходи-

мость использовать аппарат разностных уравнений. Особенно про-

сто записывать разностные уравнения, если численность каждого

следующего

поколения

t+1

зависит только

от

численности преды-

дущего

поколения

Это справедливо для популяций

неперекры-

вающимися поколениями, например многих видов насекомых. При

таком рассмотрении уравнение (VIII.2.1) превращается

уравне-

ние

t+1

F(N

), (VII

1.2.5)

или

Рассмотрим разностный аналог рассмотренного логистического

уравнения (VIII. 2.3), для

чего

запишем его

виде

dN/dt

= rN(l—

N/K).

Здесь

г —

коэффициент естественной скорости роста популяции,

—

максимально возможная

ее

численность, допускаемая

ем-

костью среды. Заменим dN/dt

на

AN/At,

где AN = N

t+1

— N

—

разность численностеи

последовательные моменты времени, Д/=1.

Тогда

t+1

= N

[l+r(l—N

/K)].

(VIII.2.6)

Однако если

какой-то момент времени значение численности

ста-

новится

больше определенной величины:

> К (1 +

г)/г,

то

уравнение (VIII.2.6)

дает

отрицательное значение

t+1

. Это свя-

зано

видом функции

/ (N

) = 1 + г

— NJK),

изображен-

ной

на

рис.

127.

Таким образом, уравнение (VIII.2.6) биологически

не

корректно. Непрерывный аналог логистического уравнения

сво-

боден

от

этого недостатка,

так как в нем при

стремлении функции

/ (N)

= г (1 —

NIK)

нулю

стремится

нулю

скорость возрас-

тания

N:dN/dt.

Для

того

тобы исправить недостаток уравнения (VIII.2.6),

сле-

дует

взять

качестве

(Л',) функцию, асимптотически стремящуюся

нулю

при

-*- оо.

част-

g ности, может быть выбрана

функция

ехр [г (1 —

/K)]

expr

фу

р (

(рис.

127,

Б).

Уравнение

(VIII.2.7)

может быть рассмотрено

в ви-

Рис.

127 Вид

функции /(ЛГ,).

А-[1+ **

разностного аналога логи-

]

;

Б — ехр

{/-(I—

Ni/K)}

стического уравнения.

290