Санагурський Д.І. Об’єкти біофізики: монографія
Подождите немного. Документ загружается.


271
також частково її структура. Такий підхід, де за відомою
структурою системи можна її формалізувати для чисто
теоретичного дослідження, називають феноменологічним.
Досліджуючи біологічні системи за приналежністю
елементів до певного класу, можна включити в опис будь-яку
кількість елементів направленої дії на реалізацію близьких за
змістом феноменів. Так, за поняттям інтеграції метаболічних
систем (К.А. Кафиани, А.Г. Маленков, 1976; В.П. Скулачев, 1972)
опис у термінах математики на рівні клітини можна проводити із
залученням усієї відомої інформації про стан клітини, включаючи
біохімічні, біофізичні та інші параметри. Власне, наближено
описувати можна за такою схемою: нехай метаболічна система В,
яка складається з m елементів (i = 1, 2,…., m), володіє функцією
відгуку
()
tХ . Відомо, що більшість внутрішньоклітинних
процесів проходить у коливальному режимі і якимось чином
взаємодіє між собою (J.W.S. Pringle, I951; П. Гленсдорф, И. При-
гожин, 1973). Можна описати такі випадки взаємодії між
коливальними елементами (Д.І. Санагурський та ін., 1978 ),
() ()
()
()
t
xtX
,t
x
tX
m
i
m
i
∏
=
∑
=
, (6.3)
де
()
t
X
i
функції відгуку елементів E
m
.
При змішаних операторах взаємодії між осциляторами
маємо
()
() ()
.mmit
x
t
x
tX
1,1,2,...;
m
i
m
i
−=
∑
+
∏
=
(6.4)

272
Далі будуємо певну систему ідентифікації, у нашому
прикладі використовуючи поняття взаємокореляційних функцій
(В.И. Грубов, А.Г. Ивахненко, 1966) зі всіма можливими їхніми
комбінаціями. На підставі цього можна побудувати шукану
структуру системи, що являє собою “грубу модель” (Д.И. Сана-
гурський, Е.А. Гойда, 1980).
Такий шлях приводить до структур, які можуть багато що
підказати у разі вивчення механізмів регулювання в клітинах, а
також у вивченні процесів генерування певної функції живими
системами.
Разом з цим підходом є низка й інших, які можуть бути
застосовані в описі біологічних систем (В.М. Глушков и др., 1978;
Т.А. Колотенко, 1978). Проте це моделі глобального характеру, які
дають змогу розглядати біологічну систему із загальніших позицій.
Іноді враховують і динамічні характеристики, що описують стан
окремих елементів, хоча в цьому разі беруть до уваги переважно
структуру вже відомого феномену, а дослідження проводять у
плані визначення його поведінкових властивостей (В. Hess, 1972; Е.
Сельков, С. Дынник, 1976). У цьому аспекті є також багато робіт, в
яких досліджено характеристики ферментативних систем (М.И.
Губанов, А.А. Утенбергенов, 1978) щодо їхньої стійкості, можливої
поведінки на певному проміжку часу.
Використовуючи ці методи, можна описувати вже відомі
структури з частково певними взаємодіями між їхніми
елементами, що зазвичай приводить до систем диференціальних
рівнянь, дуже часто нелінійних. Найважливішим етапом роботи в

273
плані формалізації завдань є отримання структурної моделі за
наявною моделлю і за одержаною в дослідах інформацією про її
складові елементи.
Отже, обмін речовин в ембріональному розвитку тварин,
його зв’язок з іонним гомеостазом і диференціюванням клітин є
однією з актуальних проблем сучасної біології. Проте низка питань
все ж залишається недостатньо вивченою. Це, зокрема, стосується
з’ясування ролі гормонів і деяких фізико-хімічних факторів у
регулюванні раннього ембріогенезу і диференціації клітин,
дослідженні взаємозв’язку внутрішньоклітинних процесів
метаболізму і супутніх ранньому ембріогенезу тварин зовнішніх
дій, з потенціалгенеруючою системою. Окрім того, немає досить
твердих переконань щодо причетності до процесів
внутрішньоклітинного метаболізму йонного гомеостазу клітини.
Однак на підставі літературних даних можна вважати, що
гормональне регулювання в клітині здійснюється вже на
початкових етапах розвитку тварин і має відношення до різних
процесів життєдіяльності клітини, зокрема, до її йонного
гомеостазу, а через нього – до генерування ТМП. За допомогою
гормональних впливів на живу систему інколи вдається
“розпізнати” окремі ланцюги регуляторних систем, оскільки часто
гормони різної природи володіють протилежно направленими
ефектами, що виявляються на однотипних ланках у живій системі.
У разі дослідження комплексу складних взаємозв’язків виникає
потреба використовувати математичний апарат, який дає змогу
побудувати їхню загальну схему.

274
6.3. Çàñîáè ³ ìåòîäè àíàë³çó
ðåçóëüòàò³â, îòðèìàíèõ
ï³ä ÷àñ åêñïåðèìåíòó
Основною властивістю досліджуваного
біологічного об’єкта, є його розвиток, а, отже, параметри, за якими
описують його стан, мають нестаціонарний характер.
Згідно з даними літератури (В.П. Божкова й ін., 1974) і
наших досліджень (С.И. Кусень и др., 1980; Д.И. Санагурський,
1983), змінам ТМП властивий коливний характер, тому
статистичне оброблення результатів потребує спеціального
підходу (Е.А. Гойда и др., 1974).
Нехай відомо декілька паралельних однотипних реалізацій
(в нашому прикладі – зміни ТМП) у часі. Опишемо це як:
(6.5)
Для отримання кожної точки кривої використано підхід,
описаний у нашій роботі (Е.А. Гойда и др., 1974).
Так, щоб отримати першу точку
(
)
[
]
t
x
01
, на підставі серії
спостережень, описаних формою (6.5), необхідно:
(
)
∑
= /n
x
t
x
i10
.
(6.6)
()
() () () ()
()
(
)
(
)
(
)
(
)
()
() () () ()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
=
=
..............................
t
x
,...,t
x
,t
x
,t
x
T
X
t
x
,...,t
x
,t
x
,t
x
T
X
t
x
,...,t
x
,t
x
,t
x
T
X
1n
131211
2
0n030201
1
nn
n3n2n1
n

275
Границі змін досліджуваного показника
(
)
t
x
0
в певний
момент часу будуть:
(
)
(
)
(
)
[
]
() () ()
[]
⎩
⎨
⎧
−=
−=
t
x
t
x
t
x
Δ
t
x
t
x
t
x
Δ
0j1min0min
0i1max0max
. (6.7)
Аналогічні операції роблять із рештою послідовністю точок,
коли обов’язковою умовою є облік фіксації часу при отриманні
кожної точки.
Подібні ж операції здійснюють для масивів, одержаних при
дії гормонів, антибіотиків і цитостатиків.
Для знаходження достовірних або недостовірних відміннос-
тей у експериментах можна використати стандартні програми, які
дають змогу підраховувати не тільки відмінності між контролем і
дією, але і між однотипними впливами різної сили.
Оскільки в роботі використовували результати дослідження
ТМП у середовищах, що містять компоненти, які можуть впливати
на окремі ланки метаболізму, то було цікаво з’ясувати в першому
наближенні взаємовідношення між деякими процесами метаболіз-
му клітин, а також між вивченими в цих умовах біофізичними
параметрами.
Наприклад, використовували підхід (Д.І. Санагурський,
О.А. Гойда, 1980), коли за елементарними системними позиціями
було узагальнено поняття про властивості систем, а також
розглянуто завдання відтворення структури системи, що генерує
певну властивість за набором характеристик елементів. Отже,
передбачено набір елементів E
1
, E
2
, E
3
,..., Е
n
. Потрібно відтворити

276
структуру системи, використовуючи характеристики елементів. За
співвідношенням для обчислення взаємокореляційної функції
() () ( )
dtτtytx
τT
1
τ
R
τT
0
y
i
x
i
∫
+
−
=
−
(6.8)
та з урахуванням повної парної комбінації характеристик
елементів, отримаємо:
() ()
∫
=
C
τ
R
gradτ
RC
2
n
y
i
x
i
y
i
x
i
z
n
, (6.9)
де
()
t
R
y
j
x
i
– значення взаємокореляційної функції;
(
)
tx і
()
τty + – тимчасові характеристики елементів E
і
,
що входять у
систему.
За співвідношенням (6.9), можна побудувати кореляційний
профіль, одержаний при розрахунку
(
)
τ
R
y
j
x
i
всіх можливих
комбінацій характеристик E
і
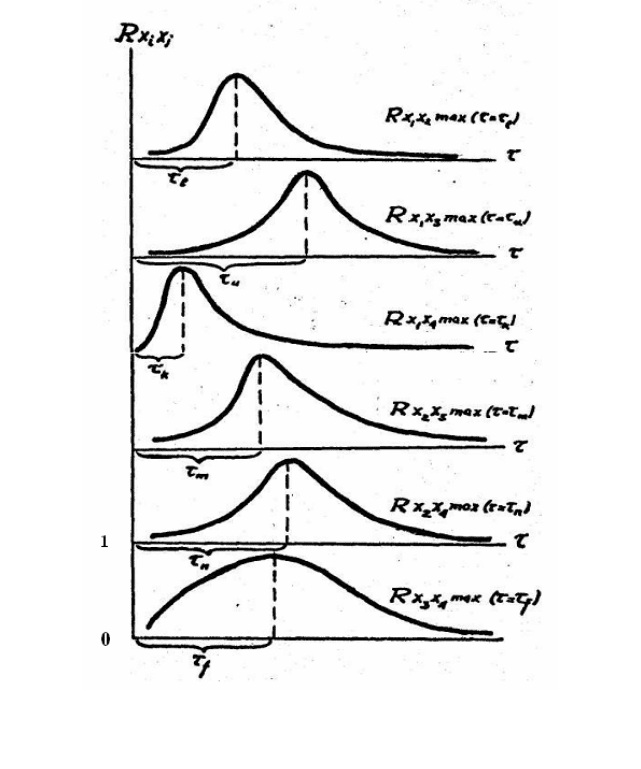
, що входять у систему (рис. 6.7).
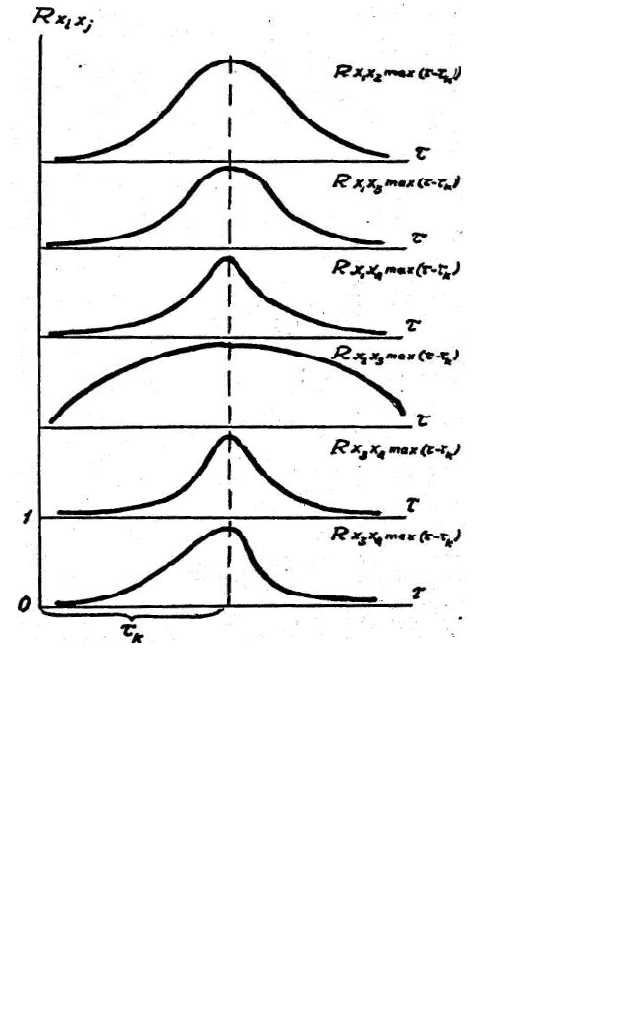
Приклад з повним збігом усіх максимумів – ідеальний для
розрахунку кореляційного профілю, й, отже, τ – const (рис. 6.8).
Використовуючи значення
(
)
τ
R
y
j
x
i
при τ
1
, τ
2
і т.д. (рис. 6.7),
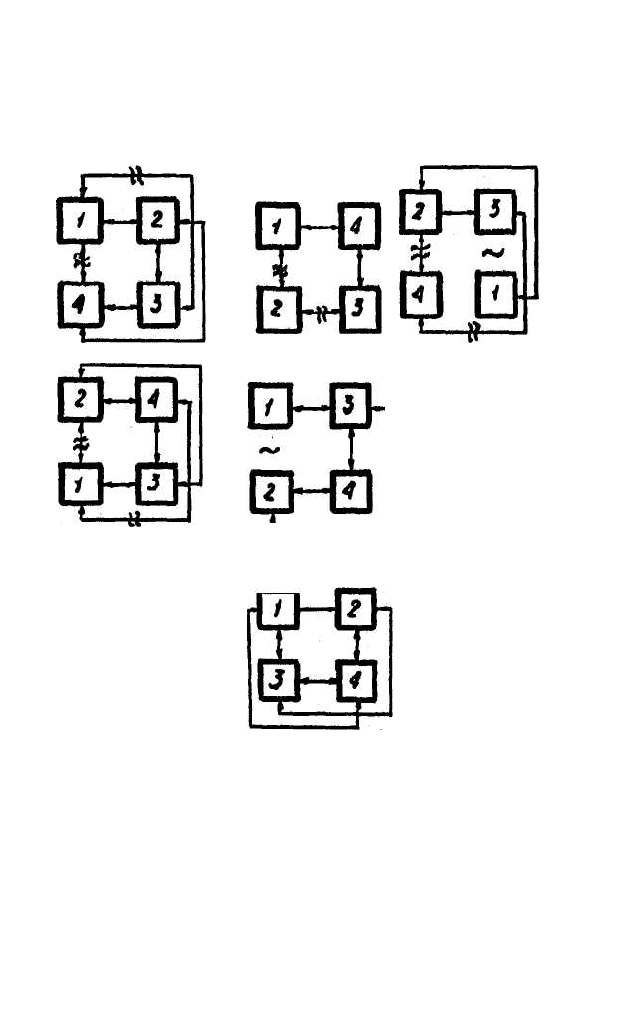
отримаємо низку структур, зображених на рис. 6.9. Тут розглянуто
комбінацію з чотирьох елементів. Як видно з рис. 6.9, для кожного
фіксованого τ є певна структура, тобто можна говорити про
“розвиток” системи в часі. Структуру, зображену на рис. 6.9,
вважають фіксованою, оскільки всі максимуми
(
)
τ
R
y
j
x
i
належать
до одного τ.
277
Рис. 6.7. Кореляційний профіль, одержаний при розрахунку всіх можливих
комбінацій для чотирьохелементної системи
278
Рис. 6.8. Ідеальний приклад розрахунку кореляційного профілю для
чотирьохелементної системи
Аналітично такі структури можна описати матрицями
стану складної системи (6.10),
де
()
(
)
(
)
K
max
K
K
y
j
x
i
max2
2
y
j
x
i
max1
1
y
j
x
i
τ
...
τRτR
〉〉〉
.
Компонентами матриці служать значення
(
)
K
max
k
y
j
x
i
τ
R
у
порядку зростання τ ( перший рядок ). Кожен стовпець містить
279
значення кореляційних функцій за градієнтом зменшення їхніх
абсолютних значень у відповідний момент часу τ для першого
стовпчика – τ
1
, для другого – τ
2
, і для k – τ
k
.
Рис. 6.9. Структури, які відповідають кореляційним профілям, що
зображені на рис. 6.7
Рис. 6.10. Структура кореляційного профілю, зображеного на рис. 6.8
За значеннями
(
)
(
)
n
max
1
y
j
x
i
K
max
1
R
y
j
x
i
τR
...,τ
першого
стовпця будуємо структуру системи для моменту τ
1
, елементи якої
описуються безперервними функціями, що дають змогу
розрахувати всі комбінації взаємокореляційних функцій.

280
Аналогічно чинимо і з іншими стовпцями. При рівності значень
()
K
max
k
y
j
x
i
τ
R
і
(
)
1K
max
k
y
j
x
i
τ
R
+
характерне розгалуження
структури або наявність зворотних зв’язків у такій системі. У разі
max
2
max
1
ττ
= (всі максимуми кореляційних функцій відповідають
одному фіксованому значенню τ) можна говорити про наявність
єдиної композиції елементів, які генерують певну функцію на всіх
проміжках її вивчення.
(6.10)
Матриця стану структури має вигляд:
(
)
()
()
maxk
1
y
j
x
i
max2
2
y
j
x
i
max1
1
y
j
x
i
τR
.....................
,
τR
,
τR
(6.11)
і являє собою вектор-стовпець.
Властивість (6.11) використовують для перевірки точності
однотипної паралельної реалізації. Якщо всі максимуми
(
)
τ
R
y
j
x
i
відповідають одному фіксованому τ, то можна оцінити точність
використовуваного методу, ступінь стаціонарності досліджуваного
явища.
