Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1

Подождите немного. Документ загружается.

Итак, оказывается, что при прямолинейно-параллельном потоке

имеем:

при п = 0 постоянное понижение давления А р с на стенке

галереи;

при п = 1 постоянный расход жидкости Qc через стенку галереи

площадью а;

случай п = -1 соответствует включению мгновенного плоского

стока на стенке галереи; этим стоком мгновенно в начальный

момент был отобран объем жидкости V с через стенку галереи

площадью ст.

Для каждого из этих трех случаев определим величину D из

равенств (6.26)-(6.28), выразив ее соответственно через величины

А Рс, Q c Vc-

Подставляя найденные значения константы D в формулу (6.19)

и полагая в ней последовательно п = 0, 1, -1, получаем

распределение давления в прямолинейно-параллельном потоке, в

котором на стенке галереи выдерживается соответственно посто

янным либо понижение давления, либо расход жидкости, либо

проведено включение мгновенного стока

Именно:

bp = A pce rfc ^ ^ j при л = 0 ,

Л 2 jaVk7 . ^ £

Ap = Q c k^~ie,fC^ T прип= 1,

4К1

при п = -1 .

(6.29)

(6.30)

(6.31)

Как и следовало ожидать, формула (6.31) совпадает с формулой

(3.28), в которой величина У ж равна объему жидкости, мгновенно

отобранной из галереи при притоке к ней жидкости с двух сторон,

т.е. при работе бесконечного пласта, а не полубесконечного, как

в задаче, рассматриваемой в данном параграфе.

Формула (6.30) отличается лишь множителем 2 от формулы

(4.13), в которой величина Qc была равна постоянному расходу

жидкости через две (а не через одну, как в данной рассматриваемой

задаче) взаимно противоположные стенки галереи при притоке к

ней жидкости с двух сторон в условиях бесконечного пласта.

Формула (6.29) совпадает с формулой (6.13), ибо решение Коши (6.6)

получается из решения Хартри (6.15) при п = 0 как частный случай.

Если считать, что уравнение (6.1) представляет собой не

дифференциальное уравнение пьезопроводности, как было принято

при выводе всех формул (6.19)-(6.31), а дифференциальное

уравнение расхода, то решение Хартри (6.18) можно с учетом

равенства (6.3) переписать так*:

Правые части формул (6.19) и (6.32) одинаковы, но они

определяют разные величины, стоящие в левых частях этих формул,

полученных при решении разных дифференциальных уравнений —

пьезопроводности и расхода.

Чтобы получить при \ = 0 постоянный расход Qc жидкости через

стенку галереи, надо принять в формуле (6.32) еще и п = 0:

Определив с помощью равенства (6.33) значение постоянной

величины D, из формулы (6.32) найдем при п = 0 распределение

расхода жидкости в прямолинейно-параллельном потоке, считая,

что с начального момента t =* 0 расход жидкости Qc через стенку

галереи удерживается постоянным:

Как и следовало ожидать, формула (6.34) совпала с формулой (6.14).

В 1948 г. Рибо** опубликовал три статьи [945], [946], [947],

посвященные интегрированию дифференциального уравнения типа

теплопроводности для простейшего случая прямолинейно-парал-

лельного потока.

Сам Хартри рассматривал решение только дифференциального уравнения теп

лопроводности, совпадающего по существу с дифференциальным уравнением пье

зопроводности.

Густав Рибо был действительным членом французской Академии Наук по сек

ции общей физики отделения математических наук.

(6.32)

QC = D = const.

(6.33)

(6.34)

§ 3. Решения Рибо и Нордона для

прямолинейно-параллельного потока

Приняв

V /

где

w =

(6.36)

Рибо свел интегрирование дифференциального уравнения в

частных производных (6.1) к интегрированию следующего обыкно

венного дифференциального уравнения:

В своих исследованиях решений уравнений (6.35) и (6.37) Рибо

ограничился только тем случаем, когда величина т равна либо нулю,

либо любому полуцелому числу (т.е. когда Ъп равно целому числу).

Рибо отметил, что при т = О его решение (6.35) сводится к

решению Коши (6.6) и уравнение (6.37) сводится к дифференци

альному уравнению (6.9), полученному Коши.

По-видимому, Рибо не знал о работе Хартри [853]*, опублико

ванной в сравнительно малоизвестном английском журнале в 1935 г.,

т.е. на 13 лет ранее публикации статей Рибо. Поэтому Рибо не

использовал введенные Хартри кратные интегральные дополни

тельные функции ошибок inerfc w для решения обыкновенного

дифференциального уравнения (6.16), совпадающего с уравнением

(6.37), если принять 2т = п. Найденные Рибо многие свойства

функции f т (w ) как-решения дифференциального уравнения (6.37)

выводятся гораздо проще как свойства кратных интегральных

дополнительных функций ошибок.

Для частного случая m = 1/2 (соответствующего случаю п = 1 в

решении Хартри) Рибо нашел следующее выражение для функции

Работа Хартри получила широкую известность лишь после упоминания о ней

и ее использования в новейших (начиная с 1947 г.) изданиях монографии Карслоу и

Егера [350].

/"(w) + 2w/'m(w)-4rn/m(w) = 0.

(6.37)

/vi(w):

/^(w) = e w2- Vn"w 1 - Je 22dz

(6.38)

и табулировал эту функцию. Совершенно очевидно, что найденная

и табулированная Рибо функция/i^(w), определенная равенством

(6.38), равна Jnierfcw — см. формулы (П. 16), (П. 17), (Г1. 33).

Исследованная Рибо при т = 1/2 задача теории теплопро

водности соответствует случаю постоянства величины теплового

потока черс { плоскую стейку, ограничивающую ирямолинейпо-

параллельпый ноток. Для условий . именно этой задачи Рибо

заметил, что графики зависимости температуры от координаты

, определяющей положение точки в прямолинейно-параллель

ном потоке, будут гомотетичными (определение гомотетии смот

реть дальше) кривыми по отношению начала координат с

коэффициентом гомотетии 7F.

Это подмеченное Рибо интересное свойство графиков удобнее

пояснить и прокомментировать, пользуясь решением задачи теории

фильтрации, соответствующей решенной Рибо задаче теории

теплопроводности. Именно, как было доказано в двух предшест

вующих параграфах, рассмотренный Рибо случай т = 1/2, т.е.

/? = 1, в прежних обозначениях соответствует неустановившемуся

прямолипейпо-параллельному фильтрационному потоку жидкости,

в котором с начального момента был установлен постоянный ее

расход через стенку галереи. Формула (6.30) для определения

понижения давления Ар (|, t) в любой точке потока в любой

момент может быть переписана так:

Из формулы (6.39) следует, что графики зависимости А р от

Ч> будут обладать особыми свойствами. Именно допустим, что с

использованием формулы (6.39) построены два графика зависимости

от | для моментов t\ и Х2 (см. рис. 6.2). Очевидно, что,

взяв на первом графике (для момента t\) любую точку' Рх с

координатами (Ар х ,| i ) и умножив эти координаты на величину

t j , получим точку Р2 с координатами ( А р 2,1 2) н& втором

графике (для момента t2), причем

(6.39)

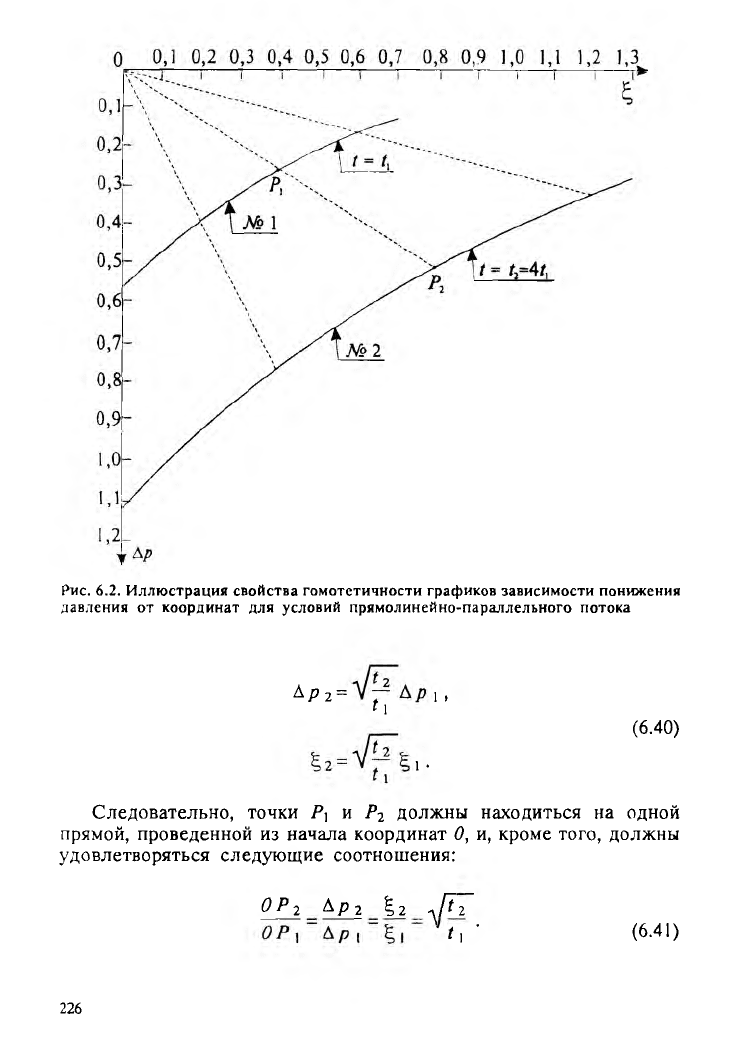
Рис. 6.2. Иллюстрация свойства гомотстичности графиков зависимости понижения

давления от координат для условий прямолинейно-параллельного потока

Л/>2 = 1,

1 1

(6.40)

1 •

Следовательно, точки Р\ и Р2 должны находиться на одной

прямой, проведенной из начала координат 0, и, кроме того, должны

удовлетворяться следующие соотношения:

0Р2 А р 2 ^2 д/^2~

f, ’ (6.41)

Отмеченные свойства графиков, отражаемые соотношениями

(6.40) и (6.41), указывают на то, что кривые линии, служащие

графиками изучаемой зависимости понижения давления от коор

динаты, оказываются подобными, причем с центром подобия в

начале координат и с постоянным коэффициентом подобия. Такое

подобие кривых называется гомотетией.

Действительно, приведем определение гомотетии, как оно

дается в математической энциклопедии [273] на стр. 1061-1062:

«Гомотетия — преобразование Эвклидова пространства относи

тельно некоторой точки 0 (центра гомотетии), ставящее в соот

ветствие каждой точке Р\ точку Ръ лежащую на прямой 0Р{ по

правилу

0Р2= к0Р , ,

где к — постоянное число, называемое коэффициентом гомотетии

Гомотетия есть частный случай подобия».

На рис. 6.2 кривые № 1 и № 2 построены для таких моментов

11 и t2i что t2 = 41\. Поэтому, как это очевидно из соотношения

(6.41), 0Р2 = 20PV

Нордоп — ученик Рибо — обобщил его решения. Именно выше

было упомянуто, что Рибо получил свби решения, предположив,

что число т в уравнении (6.37) и в формуле (6.35) является либо

полуцелым, либо равным нулю. Нордои [920] рассмотрел более

общий случай, когда число т могло быть любым действительным

числом, и нашел соответствующее решение, выраженное с помощью

функций Вебера.

Решения Нордона уже были указаны в § 4 главы 4, они представ

лены формулой (4.146).

§ 4. Обобщенное решение автомодельной задачи,

связанной с одномерными неустановившимися потоками

в многомерном пространстве

В двух предыдущих параграфах приведены полученные Хартри,

Рибо и Йордоном решения автомодельных задач только для условий

прямолинейно-параллельных потоков, изучение которых приводило

к необходимости интегрирования дифференциальных уравнений

типа (6.1).

Поставленные и решенные упомянутыми авторами задачи,

несомненно, заслуживали внимания сами по себе, но, кроме того,

и потому, что их решения породили введение новых весьма

полезных

трансцендентных функций — кратных интегральных дополнитель

ных функций ошибок. Однако удивительно, что эти задачи были

поставлены и решены лишь спустя много лет не только после

работ Фурье и Лапласа, заложивших основы математической

(аналитической) теории теплопроводности, но и после классических

работ Томсона и Рэлея в той же области.

После ознакомления с работами Хартри, Рибо, Нордона,

выполненными в 1935-1949 годах, автору показалось не менее

удивительным, что в последующие 20 лет не было выполнено

естественно напрашивающегося обобщения решений этих же авторов

на случаи плоско-радиального и радиально-сферического потоков.

В данном параграфе описывается обобщенное решение автомо

дельной задачи, справедливое для одномерных неустановившихся

потоков не только в пространстве одного, двух и трех измерений,

но, вообще, в любом многомерном пространстве.

Итак, вместо уравнения (6.1) будем решать более общее

дифференциальное уравнение пьезопроводпости для одномерного

неустановившегося потока в пространстве ( а + 1 ) измерений,

которое записывается так — см. § 2 главы 3:

э_2_4/>. « ёАл _ i <L&£ (И2, (6-42)

Э12 1 Э1 К д t

Считая в начальный момент t = 0 поток невозмущенным, будем

иметь такое начальное условие:

Др(£0)*(Д/>),=0*=0. (6.43)

Уравнение типа (6.1), рассматривавшееся в трех предыдущих

параграфах и относящееся только к прямолинейно-параллельному

потоку, получается из уравнения (6.42) при а = 0.

Обобщая результаты, изложенные в двух предыдущих парагра

фах, будем, следуя статье [755], искать решение дифференциаль

ного уравнения (6.42) в таком виде:

: 2

Ар t) - A tsf s I | A t f s (w ), (6.44)

P2 (6.45)

4k t

где s — любое действительное число, f s ( w ) — искомая функция.

Размерность и значение постоянной величины А и природа функции

fs(w) зависят, конечно, от величин а и s.

Для определения функции Л(\у) надо подставить величину

Ар из (6.44) в (6.42), чтобы получить обыкновенное дифференци

альное уравнение, сопряженное дифференциальному уравнению в

частных производных (6.42).

Так как уравнение пьезопроводности (6.42) отличается от

уравнения расхода (5.5) только знаком при величине а и так как

равенства (6.44) и (6.45) вполне аналогичны равенствам (5.35) и

(5,36), то можем не повторять промежуточные выкладки, прове

денные в § 4 главы 5, и сразу записать искомое обыкновенное

дифференциальное уравнение, которое будет отличаться от ана

логичного уравнения (5.37) лишь знаком перед величиной а:

I + а

'( W )~sfs( W ) = 0, а = 0, 1,2,3...

(6.46)

Уравнение (6.46) является сопряженным дифференциальному

уравнению пьезопроводности (6.42).

Решение полученного обыкновенного линейного дифференци

ального уравнения с переменными коэффициентами (6.46) может

быть найдено тем же способом, который был подробно описан в

§ 4 главы 5 применительно к уравнению (5.37). Именно решение

уравнения (6.46) получим, изменив лишь знак перед величиной

а в равенстве (5.52):

f s(w) = Be

1+ а 1 + а

(6.47)

где В — постоянная величина.

По поводу этого найденного решения сопряженного диффе

ренциального уравнения (6.46) смотреть еще Примечание III в конце

данного параграфа.

Подставляем выражение функции f s(w) из (6.47) в (6.44),

обозначая произведение постоянных множителей Л • В новой по

стоянной величиной С и учитывая еще соотношение (6.45):

A p(l,t) = Ctse

S +

1 + а 1 +а в £;2

4 Kt

(6.48)

Заметим, что рассмотренная здесь автомодельная задача была

поставлена в статье автора [755]. Однако вместо подстановки (6.44)

в той статье была выбрана более сложная подстановка, что привело

и к более сложному виду сопряженного обыкновенного диффе

ренциального уравнения, чем уравнение (6.46). Хотя в статье [755]

интегрирование сопряженного уравнения было выполнено лишь

для трех частных случаев, когда а = 0, 1,2, но в результате этого

были получены обобщения задач Коши, Хартри, Рибо, Нордона на

случаи плоско-радиального и радиально-сферического потоков.

Используя решение (6.48), справедливое для одномерных

потоков в любом многомерном пространстве, легко получить

решения для каждого из трех простейших одномерных потоков —

прямолинейно-параллельного (при а-0), плоско-радиального (при

а=1) и радиально-сферического (при а = 2).

Рассмотрим эти три частных случая.

1 случай. Применительно к прямолинейно-параллельному по

току полагаем в формуле (6.48) а = 0 :

Ap(l,t) = Ctst

4к t

s +

I i._ £ i

2’2’4кt

(6.49)

Формула (6.49) справедлива, если s есть любое рациональное

число. Рассмотрим более частный случай, когда s принимает лишь

положительные целые или иолуцелыс значения, включая пуль, т.е.

допустим, что

, п = 1,2,3...

(6.50)

Пользуясь формулой (П. 337), переходим от ВГФ II рода к

интегральной дополнительной функции ошибок;

1111

— +

--------

= 2 п 1 VrT е '***' iп 1 erfc

V4kT *

(6.51)

Учитывая равенства (6.50) и (6.51), переписываем форму

лу (6.49):

(6.52)

Поставим такое граничное условие: будем считать, что при

-0, т.е. на стенке прямолинейно-параллельного потока, давление

задано как одночленная степенная функция времени:

p(Of/) = D„/

(6.53)

где Dn — заданная постоянная величина, размерность которой зави

сит от п.

Полагая в формуле (6.52) | = 0, учитывая граничное условие

(6.53) и равенство (П. 36), получаем:

п - 1

Ct^r 2n-'Jn-

П - 1

>*-1

п + 1

откуда

С = Р „

(6.54)

Подставим (6.54) в (6.52):

Ар(1, 0 = 2п-'Г^П + 1

П - 1

* i

in~'elfcl k 7

(6.55)

или

Др(|,0 = 2п-1Г

Ар (0,t)in’ 1 erfcj^ Kt , п = 1,2,3...

(6.56)

Рассмотрим частный случай n= 1, что соответствует значению

s - О — см. равенство (6.50).

Тогда формула (6.56) упростится и примет вид:

Л р (11» t ) ^ А р ( 0, /) ег/с