Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1

Подождите немного. Документ загружается.

ИСПОЛЬЗОВАНИЕ МЕТОДА ИНТЕГРИРОВАНИЯ ПО КООРДИНАТАМ

СТОКООБРАЗНЫХ РЕШЕНИЙ

§ 1. Вводные замечания о методе интегрирования

стокообразных решений

Как уже упоминалось в § 1 главы 4, идея и использование

метода интегрирования стокообразных решений принадлежат Том

сону [966]. Существенное развитие применения этого метода было

сделано Рэлеем [944]; такое название метода было впервые

применено в монографии Карслоу и Егера [350].

В главе 4 был использован метод интегрирования стокообразных

решений для перехода от ранее найденных решений, относящихся

к мгновенным стокам (или источникам), к исследованиям непре

рывно действующих стоков. При этом переходе проводилось

интегрирование по времени стокообразных решений.

В данной главе будет использоваться интегрирование по

координатам ранее найденных стокообразных решений. Именно

интегрируя стокообразные решения по координатам, будут осуще

ствляться переходы:

1. От точечных стоков в пространстве к прямолинейным.

2. От прямолинейных стоков в пространстве к плоским.

3. От точечных и прямолинейных стоков в пространстве к

поверхностным. В итоге первых двух из только что названных

переходов будут получены ранее уже выведенные формулы, а в

результате третьего перехода — новые формулы, связанные, по

существу, с решением неавтомодельных задач*.

Для иллюстрации метода интегрирования стокообразных реше

ний по координатам было достаточно ограничиться в данной главе

только мгновенными стоками. И мгновенные и непрерывно дейст

вующие прямолинейные, поверхностные и объемные стоки —

источники исследуются в последующих главах иными методами.

См. напоминание условий автомодельности задач в § 1 главы 6.

§ 2. Применение метода для перехода

от мгновенного точечного стока в пространстве

к мгновенному прямолинейному

В § 2 главы 3 был пояснен физический смысл фундаментальных

решений уравнения пьезопроводности. Эти фундаментальные ре

шения (3.1)—(3.3), полученные Лапласом, Рэлеем и Томсоном,

характеризовали неустановившиеся процессы перераспределения

давлений после включения в пространстве соответственно плоского,

прямолинейного и точечного мгновенных стоков. Для понижений

давления эти решения были затем записаны в форме (3.28)—(3.30).

Если принять за известное фундаментальное решение (3.3) или

(3.30) для точечного стока в пространстве и проинтегрировать

его по координате, то можно получить фундаментальное решение

(3.2) или (3.29) для прямолинейного стока в пространстве. Докажем

это. Допустим, что в начальный момент f=0 был на одно мгновение

включен сток в точке 0, в которой поместим начало декартовых

координат (рис. 8.1). Тогда в условиях плоско-радиального потока

понижение давления Ар в любой точке наблюдения Р (д*, у, z) в

любой момент t определим по формуле (3.30), считая, что точечный

сток мгновенно отобрал жидкость объемом V ж:

где г — расстояние от точки Р до точечного стока в начале коор

динат 0; остальные обозначения были объяснены в главе 3.

Допустим, что вместо мгновенного точечного стока в точке 0

имеем вдоль оси у мгновенный прямолинейный сток малой длины

dy (см. рис. 8.1). Пусть этот прямолинейный сток малой длины dy

мгновенно поглотил в начальный момент количество жидкости

объемом V ж, но на единицу длины объем поглощенной жидкости

равен V т.е.

Перейдем к рассмотрению мгновенного прямолинейного стока

неограниченной длины, совпадающего с осью у. Чтобы определить

понижение давления в любой точке Р в окрестности такого

8(Л1С#)%Р* 8 (л к ^ р* е

(8.1)

V* = V'xdy.

(8.2)

Рис. 8.1. Точка наблюдения Р (х, у, z) и сток в начале координат О

линейного стока, надо подставить в формулу (8.1) V ^dy вместо

V ж и, основываясь на методе суперпозиции, выполнить интеграцию

по координате у в пределах от - °о до + °о.

Тогда получим:

8(лкО н Р*

X + Z+ 00 у

- 4кг г ,

е J е dy.

(8.3)

Сделаем замену переменной, положив

^ = = u; dy = 'l4Ktdu.

(8.4)

Поэтому

Je dy = 'l4Kt\ e~u* du.

+00 2 +оо

^ (8-5)

Интеграл в правой части последнего равенства представляет

собой известный табличный интеграл. Именно

-н»

J е “ du - Vn.

(8.6)

Учитывая равенства (8.5) и (8.6), формулу (8.3) можно перепи

сать так:

X +Z

■ < 8 - 7 )

Обозначим через £ кратчайшее расстояние от линейного стока

(от оси у) до той точки Ру в которой определяется понижение

давления Ар:

Ц,=АР = т1х2 + 2 ? , (8.8)

причем точка А имеет координаты (0, у, 0).

Поэтому формула (8.7) примет вид:

Ар = , о* е (8 9)

4 к к Р t

Применительно к задачам подземной гидродинамики удобнее

считать, что величина V ж представляет объем отобранной жидкости

не на единицу длины прямолинейного стока, а на ту его длину

«b», которая равна толщине (мощности) «Ь» пласта; прямолинейный

сток проходит пласт от его кровли до подошвы. Тогда, учитывая

еще равенство (1.41), связывающее коэффициенты пьезопроводно

сти и упругоемкости, вместо формулы (8.9) получим:

др = _ ^ _ е ' ^ . (8.Ю)

4nbKt

Формулы (8.9), (8.10) совпадают с формулой (3.29) или с

формулой (3.27), в которой надо положить а = 1 и Ах ~ nb.

Итак, с помощью метода интегрирования стокообразного реше

ния (8.1), соответствующего сферически-радиальному притоку

жидкости к мгновенному точечному стоку, совершен переход к

формулам (8.9) и (8.10), характеризующим плоско-радиальное

(осесимметричное) движение жидкости к мгновенному прямоли

нейному стоку.

§ 3. Применение метода для перехода

от мгновенного прямолинейного стока

в пространстве к мгновенному плоскому

Если принять за известное фундаментальное решение (3.2) или

(3.29), или (8.9) для линейного стока и проинтегрировать его по

координате, то можно получить фундаментальное решение (3.1)

или (3.28) для плоского стока. Докажем это.

Допустим, что в начальный момент t= О был на одно мгновение

включен в пространстве прямолинейный сток, отобравший на

единицу своей длины количество жидкости объемом V ж". Вдоль

прямолинейного стока направим ось у, и тогда понижение давления

Ар в любой точке Р(х, у, z) в любой момент t определится так с

помощью формулы (8.9) — см. рис. 8.2:

где г — кратчайшее расстояние от линейного стока (от оси у) до

точки Р. Кроме того, ОА=у, АВ=х, BP=z.

Пусть вместо мгновенного прямолинейного стока имеем вдоль оси

у и в плоскости ху тонкую полосу мгновенного плоского стока малой

ширины dx. Пусть этот плоский сток малой ширины в начальный

момент мгновенно поглотил на единицу длины количество жидкости

объемом V ж. Будем считать, что на единицу длины и на единицу

ширины плоского стока (т.е. на единицу площади плоской полоски)

объем поглощенной жидкости равен У ж. Следовательно,

Рассмотрим теперь мгновенный плоский сток, расположенный

в плоскости ху и имеющий неограниченную ширину вдоль оси х.

Чтобы определить понижение давления в точке Р, надо подставить

в формулу (8.11) V^dx вместо V* и, основываясь на методе

суперпозиции, выполнить интеграцию по координате х в пределах

от -оодо + oo. Тогда получим:

Сделав замену переменной, аналогичную той, которая опреде

лялась равенством (8.4), и используя опять равенство (8.5), сможем

представить формулу (8.13) в таком виде:

V’x = Vxdx.

(8.12)

(8.13)

Рис. 8.2. Точка наблюдения Р {х, у, z)\ ось у направлена вдоль прямолинейного

стока

Ар =

4 тс к Р* t

л/4л Kt с

“ЧИ

или же, если обозначить кратчайшее расстояние от плоского стока

до точки Р через и учесть, что % = z%

Ар =

---

-----

----------

2 Vrc к t р*

-то

(8.14)

Применительно к задачам подземной гидродинамики удобнее

считать, что величина V ж представляет объем отобранной жидкости

не на единицу ширины плоского стока, а на ту площадь о, которая

раина площади всей стенки пласта, вскрытого плоской галереей

длины L. При толщине пласта «6» имеем a = L b.

Тогда, учитывая еще равенство (1.41), связывающее коэффици

енты пьезопроводности и упругоемкости, вместо формулы (8.14)

получим:

Ар =

2 Vk Kt

р*

V ж

ji Vic"

-hi

2^ilcae

(8.15)

Формулы (8.14) и (8.15) совпадают с формулой (3.28) или с

формулой (3.27), в которой надо положить ос = 0 и А0 = 2а.

переход к формулам (8.14) и (8.15), характеризующим прямолинсйио-

параллельное движение жидкости к мгновенному плоскому стоку с

двух сторон.

§ 4. Переход от мгновенного прямолинейного стока

в пространстве к поверхностному мгновенному

цилиндрическому стоку

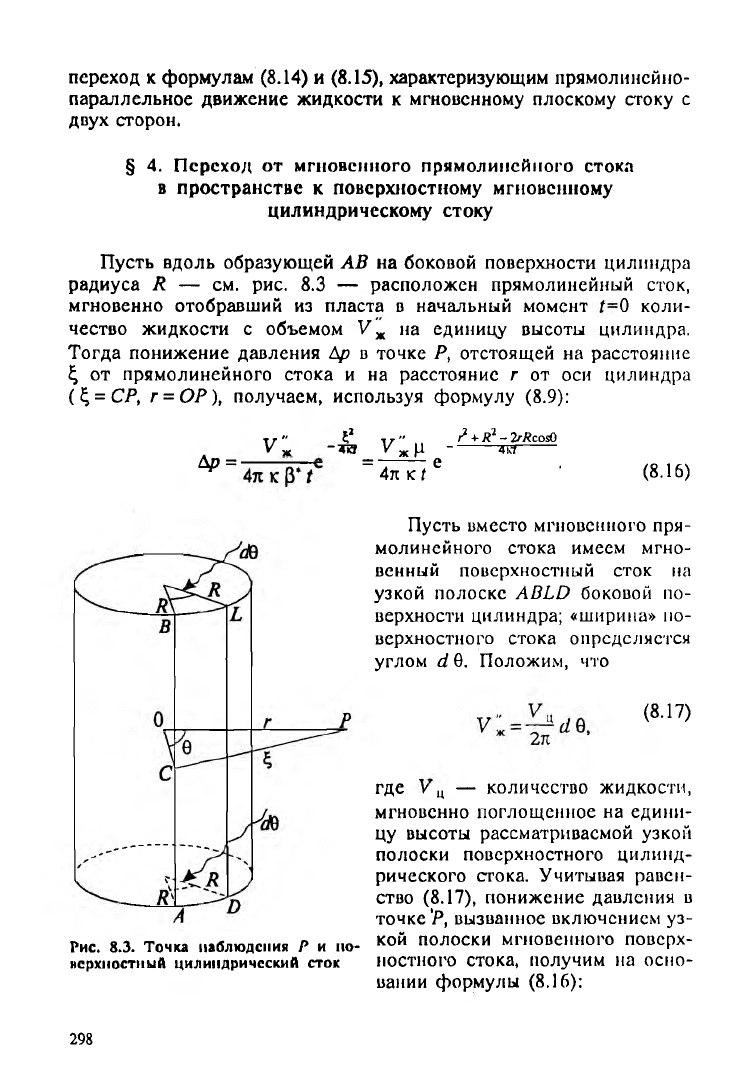
Пусть вдоль образующей АВ на боковой поверхности цилиндра

радиуса R — см. рис. 8.3 — расположен прямолинейный сток,

мгновенно отобравший из пласта в начальный момент О коли

чество жидкости с объемом V ж на единицу высоты цилиндра.

Тогда понижение давления Др в точке Р, отстоящей на расстояние

£ от прямолинейного стока и на расстояние г от оси цилиндра

(^ = СР, г = ОР), получаем, используя формулу (8.9):

тг" I2 ТГ" м ^ + *2-2r*cos0

V ж -та У ж ц

------

чтя

-----

= 4лк/е • (8.16)

АР =

Рис. 8.3. Точка наблюдения Р и по

верхностный цилиндрический сток

Пусть вместо мгновенного пря

молинейного стока имеем мгно

венный поверхностный сток на

узкой полоске ABLD боковой по

верхности цилиндра; «ширина» по

верхностного стока определяется

углом d 0. Положим, что

(8.17)

где у ц — количество жидкости,

мгновенно поглощенное на едини

цу высоты рассматриваемой узкой

полоски поверхностного цилинд

рического стока. Учитывая равен

ство (8.17), понижение давления в

точке'Р, вызванное включением уз

кой полоски мгновенного поверх

ностного стока, получим на осно

вании формулы (8.16):

/+i^-2rRcoi0

------

4*3

-----

Рассмотрим теперь мгновенный сток, равномерно распределен

ный по всей боковой поверхности цилиндра Тогда понижение

давления Ар, вызванное мгновенным пуском поверхностного ци

линдрического стока, определим, используя метод суперпозиции и

проводя в формуле (8.18) интегрирование по переменной величине

0 в пределах от 0 до 2к:

Учтем, что — см. формулу (3), стр. 224 [547] и формулу (4)

пункта 3.915 на стр. 496 [183]

где /0 — модифицированная функция Бесселя первого роДа нуле

вого порядка — см. § 6 Приложения. Подробный вывод формулы

(8.20) см., например, в § 3 главы 7 книги [401]. Тогда формулу (8.19)

можно переписать, причем применительно к задачам подземной гид

родинамики будем считать, что величина У ц равна объему жидко

сти, отобранному не на единицу высоты цилиндра, а отобранному

через всю боковую поверхность на всю высоту цилиндра, равную

толщине пласта, в котором поток жидкости к поверхностному ци

линдрическому стоку плоско-радиальный:

Такой же вывод формулы (8.21) был впервые проведен Рэлеем

[944] при исследовании мгновенного поверхностного цилиндриче

ского стока. Аналогичный результат смотреть еще, например, на

стр. 125 книги [349]. Рэлей же отметил, что при 0 формула

(8.21) вырождается *в формулу (8.9) для линейного мгновенного

стока в пространстве.

(8.19)

(8.20)

г***2

(8.21)

Формула (8.21) справедлива и при r<R и при r>R, т.е. когда

точка Р находится внутри или вне цилиндра. Если же r=Rf т.е.

когда точка Р находится на поверхности мгновенного цилиндри

ческого стока, то формула (8.21) также справедлива во все моменты,

но кроме начального (f=0). Формула (8.21) совпадает с формулой

(7.63), выведенной другим способом (при помощи предельного

перехода от окружной батареи к окружной галерее).

Выведенная Рэлеем формула (8.21) для мгновенного цилинд

рического стока используется не только в теории фильтрации и

теплопроводности, но и в других областях математической физи

ки — см., например, статью М. Д. Миллионщикова [441].

В главе 10 с помощью операционного метода будет выведена

не только формула (8.21), но и другие, более полно характеризу

ющие поле давлений в окрестности поверхностного цилиндриче

ского стока.

§ 5. Переход от мгновенного точечного стока

в пространстве к мгновенному поверхностному

сферическому стоку

Рассмотрим мгновенный поверхностный сток, равномерно рас

пределенный по поверхности сферы. Пусть в начальный момент

/=0 сферический сток мгновенно отобрал количество жидкости

объемом V Сф. Объем жидкости, добытой на единицу площади

стока, будет равен — где R — радиус сферы.

4kR*

Требуется определить пониже

ние давления Др в любой момент

времени

t в любой точке Р, вы

званное пуском мгновенного сфе

рического стока.

Для решения этой задачи выберем

на поверхности сферы какую-либо

х точку К, положение которой опреде-

-> ляется углами ф и 0 — см. рис. 8.4. В

окрестности точки К выделим эле

мент поверхности KMLN со сторона

ми (дугами на поверхности сферы)

КМ =NL=Rd 0, KN = ML = (Ksin0)

Площадь do элементарного четы-

Рис. 8.4. Точка наблюдения Р и по- рехугольника KMLN определится

всрхностный с4>сричсский сток

Объем жидкости, поглощенной в начальный момент выделенным

малым элементом сферического стока, будет равен:

~ ^ 2 ^ sin 0 dQ d(p. (8.23)

4nR2 4 n T

Для простоты подсчетов точку Р поместим на оси у, считая,

что ОР = г, КР = £>, причем

= г2 + R2 - 2rR cos0. (8.24)

Для определения понижения давления d(Ap) в точке Р>

вызванного только выделенным элементом сферического стока,

воспользуемся формулой (8.1), справедливой для мгновенного

точечного стока:

d(Ap) =

---------

у. е ^ sin 0 dQ dip. (8.25)

4к(-4тск/)%р* т

Понижение давления Ар в точке Р, вызванное пуском всего

мгновенного сферического стока, определим, учитывая равенства

(8.24) и (8.25):

я2+/

- 4 кг е=л ф=2я 2Rr cos 0

или же

V e b e '^ r 2 ^ (8-26)

^ = — TSi^Je sin 0 d 0 d ф.

2 ( 4лк*) hP*J v

Вычислим интеграл: