Щелкачев В.Н. Основы и приложения теории неустановившейся фильтрации: Часть 1

Подождите немного. Документ загружается.

я 2Ягсо»В я Rr соа в

/е 40 sin 0 d 0 = - J t 1а d (cos 0) =

о о

_ 2к?Г &«**T_2Kt( та_

Л/- Le -L Л- Iе е J*

Учитывая равенство (8.27), перепишем равенство (8.26):

(8.28)

8кЛг(л к*),/4р*

(Я-г)1 (Я+г)‘-|

' 4kJ

----

ttr~

- е

Формула (8.28) справедлива и при г<Л и при r>Rt т.е. когда

точка Р находится внутри или вне сферы. Если же г = Л, т.е. когда

точка Р находится на поверхности мгновенного сферического стока,

то формула (8.28) также справедлива во все моменты, но кроме

начального (f = 0).

Формула (8.28), определяющая понижение давления в любой

точке и в любой момент после включения мгновенного повер

хностного сферического стока в начальный момент, была впервые

выведена Томсоном [966]; см. несколько иной вывод этой же

формулы на стр. 255 книги [350].

Томсон справедливо указал, что из формулы (8.28) можно

получить при R-0 формулу для случая мгновенного точечного

стока. Действительно, полагая в формуле (8.28) R=0 и раскрывая

неопределенность по правилу Лопиталя, получим:

, , . У О» -га <8.29)

Формула (8.29) совпадает с формулой (8.1) для мгновенного

точечного стока.

Понижение давления Ар (0, t) в центре мгновенного поверхно

стного сферического стока получим из формулы (8.28), раскрывая

опять неопределенность по правилу Лопиталя:

. . . . I',* -га (8.30)

4',№ ') -8 0 .Я)»Ц -' '

Если в формуле (8.29) положить г = Л и сопоставить се с

формулой (8.30), то можно сделать такой вывод: понижение

давления в центре мгновенного поверхностного сферического стока

такое, как будто бы на расстоянии R от этого центра находится

мгновенный точечный сток.

Допустим, что мгновенный точечный сток отобрал в начальный

момент /=0 такое же количество жиДкости V Сф, какое в начальный

момент отобрал мгновенный поверхностный сферический сток.

Тогда понижение давления в мгновенном точечном стоке найдем

в любой момент, полагая г=*0 в формуле (8.29):

ЕЛр М ) 1 = 8 в; • (8-31)

R=0 8 **) Р

На основании сопоставления формул (8.30) и (8.31) можно

сделать вывод, что в мгновенном точечном стоке давление

понижается в раз интенсивнее, чем в центре мгновенного

поверхностного сферического стока одинаковой интенсивности.

Чтобы найти понижение давления Ар (Л, t) на поверхности

мгновенного сферического стока, надо положить r-R в формуле

(8.28):

А „(Я.П -. <832>

^ 8я Л2(л к#)*4 рЧ

Полагая f=0 в формулах (8.28) и (8.30) и раскрывая неопреде

ленности, убеждаемся в том, что, как и следовало ожидать из

условий задачи, понижения давлений в начальный момент в центре

сферического стока и в любой другой точке (за исключением

точек на сферической поверхности стока) оказываются равными

нулю, т.е.

[Ар (г, 01 ы> = 0, [Ар (0, t)) м) = 0 . (8.33)

r*R

Для определения понижения давления в начальный момент на

поверхности сферического стока следует положить /*0 в формуле

(8.32); получаем:

[Ар (Л, 01м, = оо. (8.33а)

Следовательно, при неограниченном увеличении времени по

нижение давления во всех точках внутри, на и снаружи сферы

асимптотически стремится к нулю.

Итак, после включения мгновенного поверхностного сфериче

ского стока понижение давления при изменении t от 0 до «>

изменяется во всех точках (за исключением точек на поверхности)

от 0, достигая какого-то максимума, и затем уменьшается, стремясь

к нулю. На поверхности сферы понижение давления изменяется

от бесконечности до нуля.

Определим момент, когда понижение давления достигает

максимального значения, например, в центре сферы. Для этого

продифференцируем по времени равенство (8.30) и, приравняв

нулю производную, найдем величину fKp для искомого момента:

Для определения точек перегиба на графике понижения

давления в центре сферы надо приравнять нулю вторую произ

водную по времени, используя то же равенство (8.30). Значения

моментов tucp, соответствующих двум точкам перегиба, оказываются

таковы:

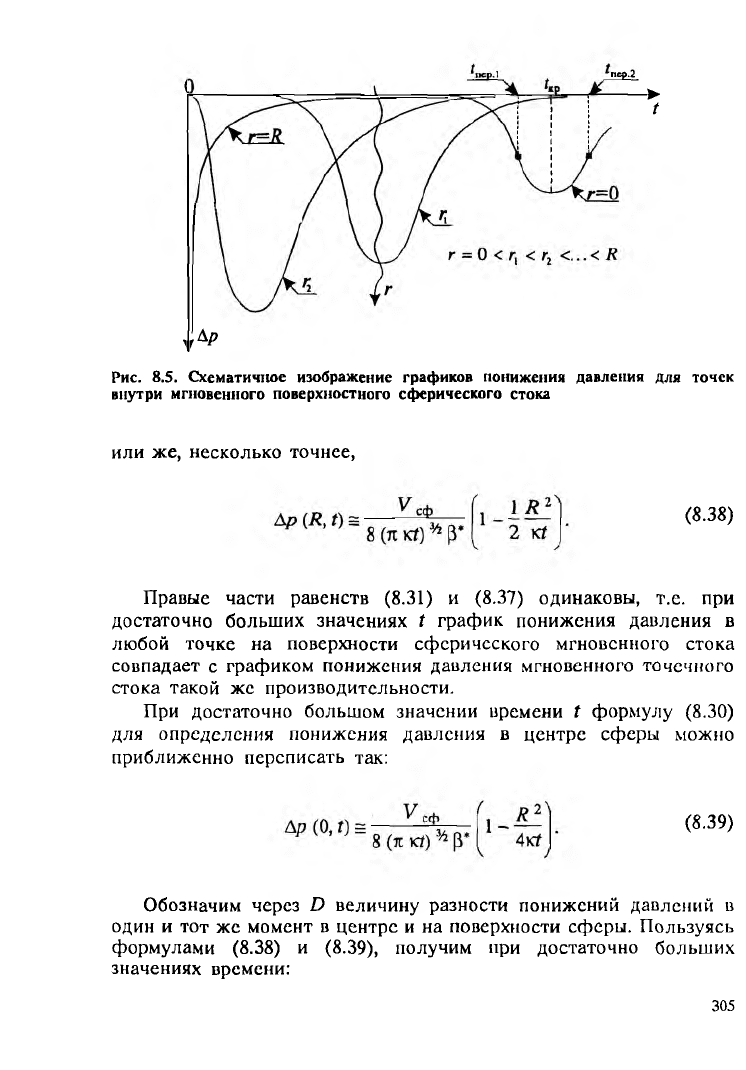
Учитывая все приведенные выше выводы, на рис. 8.5 схематично

построены графики изменения понижения давления для точек

внутри поверхности мгновенного сферического стока.

На рис. 8.5 график изменения понижения давления в центре

сферы (при г®0) является крайним и ему соответствует наименьшая

величина максимального понижения давления по сравнению со

всеми остальными графиками для точек внутри сферы. При любом

значении времени t>tKр понижение давления в центре сферы будет

заведомо больше понижений давлений в тот же момент во всех

остальных точках внутри и на поверхности сферы.

Если t настолько велико, что в разложении в ряд экспоненци

альной функции можно ограничиться первыми двумя или первыми

тремя членами ряда, то формулу (8.32) можно приближенно

переписать так:

(8.35)

/,р£(1 ±0,63) гкр.

(

пер.2

yfbP

Рис. 8.5. Схематичное изображение графиков понижения давления для точек

внутри мгновенного поверхностного сферического стока

или же, несколько точнее,

Правые части равенств (8.31) и (8.37) одинаковы, т.е. при

достаточно больших значениях t график понижения давления в

любой точке на поверхности сферического мгновенного стока

совпадает с графиком понижения давления мгновенного точечного

стока такой же производительности.

При достаточно большом значении времени t формулу (8.30)

для определения понижения давления в центре сферы можно

приближенно переписать так:

Обозначим через D величину разности понижений давлений в

один и тот же момент в центре и на поверхности сферы. Пользуясь

формулами (8.38) и (8.39), получим при достаточно больших

значениях времени:

(8.38)

(8.39)

8 (к кt)3/l р* (4 « ‘

Как и следовало ожидать, величина D оказалась положительной

(это выше уже подчеркивалось), но быстро уменьшающейся с

увеличением времени t Так, например,

где значение было определено равенством (8.35).

Заметим еще, что, ограничиваясь опять первыми двумя членами

ряда в разложениях экспоненциальных функций, формулу (8.28)

можно приближенно переписать так:

Если время t столь велико, что можно пренебречь величиной

j^2

по сравнению с числом 1, то на основании формул (8.37),

(8.39) и (8.42) обнаруживаем:

Следовательно, на поздней стадии развития процесса перерас

пределения давления (при соответственно больших значениях

времени t) понижения давления во всех точках внутри, на и снаружи

сферического поверхностного стока будут одинаковыми и одина

ково быстро стремиться к нулю.

(8.41)

8(гск*)^р* ‘

Ар (0,0 S Лр (г, 0 а 6р (Я, 0 « 8 (][F^ .

(8.43)

ИСПОЛЬЗОВАНИЕ ОПЕРАЦИОННОГО МЕТОДА ЛАПЛАСА ДЛЯ

ИССЛЕДОВАНИЯ ПРОСТЕЙШИХ НЕСТАЦИОНАРНЫХ ПОТОКОВ

§ 1. Введение

Для математической физики операционные методы особенно полез

ны потому, что с их помощью задачи интегрирования дифференциальных

уравнений с частными производными сводятся к задачам интегрирова

ния обыкновенных дифференциальных уравнений.

В первых параграфах данной главы применение операционного

метода Лапласа иллюстрируется на примерах получения фундамен

тальных решений для задач, связанных с работой трех простейших

стоков — источников: плоского в пространстве (прямолинейного на

плоскости), прямолинейного в пространстве (точечного на плоскости),

точечного в пространстве. При работе этих трех простейших стоков —

источников возникают три простейших одномерных потока: прямоли

нейно-параллельный, прямолинейно-осесимметричный (плоско-ра-

диальный) и сферический радиальный. Исследование трех простей

ших стоков — источников и соответствующих им потоков уже про

водилось разными методами в предыдущих главах. Использование

операционного метода Лапласа для исследования трех простейших

потоков нужно не только для иллюстрации особой простоты получе

ния фундаментальных решений с помощью этого метода, но и для

других целей. Именно в последующих главах операционный метод

Лапласа будет использован для исследования стоков — источников

более сложных типов. В процессе этого исследования необходимо

будет пользоваться изображениями оригиналов функций, соответст

вующих трем простейшим стокам — источникам.

Изложение операционного исчисления см., например, в книгах

[259], [260], [426]; краткое изложение см. еще в главе XIV [427] и в

главах XII, XIII [350].

§ 2. Прямолинейный сток на плоскости

(плоский в пространстве)

Будем считать, что на неограниченной плоскости в начальный

момент t=0 был включен прямолинейный сток бесконечной длины.

Этот прямолинейный сток будем рассматривать как сечение

плоского пространственного стока, который для образности будем

называть плоской галереей. Прямолинейно-параллельный поток

жидкости будет притекать к галерее с двух сторон перпендикулярно

к ее стенке. На рис. 3.3 изображен в плане участок галереи, т.е.

отрезок ЛОВ прямолинейного стока.

Примем, что через участок стенки* галереи с площадью 2о в

начальный момент мгновенно был отобран объем жидкости Уж.

Поле давлений в начальный момент было невозмущенным. Требу

ется определить процесс перераспределения давления после

мгновенного включения стока. Обозначим понижение пластового

давления через Др; начало координат 0 поместим на прямолинейном

стоке и ось абсцисс х направим перпендикулярно к нему.

Математически задача ставится так: понижение давления

Др (jc, t) в любой точке, зависящее от времени t и координаты я,

должно удовлетворять дифференциальному уравнению пьезо про-

водности:

= 1 1 Д£ * >0 1>0 («•!)

га? к В t • ■ ■

где к — коэффициент пьезопроводности.

Кроме того, учитывая начальное условие, количество мгновенно

отобранной из пласта жидкости и условие на бесконечности,

должны удовлетворяться следующие соотношения:

Др = 0 при? = 0, 0<л:<оо} (9.2)

Vж = 2g р* J* Ар d x , f = О,

(9.3)

Ар = 0 при 0 < f < х = (9.4)

где [J* — коэффициент упругоемкости пласта.

Как принято, будем называть искомую функцию Д р (.х, t)

оригиналом, ее изображение по Лапласу будем обозначать одно

именной прописной (большой) буквой: АР fas), где аргумент s

функции-изображения служит параметром преобразования. Как

*Площадь обозначена через 2 а, так как приток жидкости к галерее учитыва

ется с двух сторон.

символ преобразования Лапласа используется буква L. Поэтому

переход от оригинала Ар (*, t) к изображению АР (.х, 5*) при

проведении преобразования Лапласа записьшается так:

L [ Ар (х, t) ] = Д Р (х, s) = J е А р (х, t) dt. (9.5)

Подвергнем уравнения (9.1)—(9.4) преобразованию Лапласа.

Тогда, следуя правилам операционного исчисления, которые будем

считать известными, получим:

Как и следовало ожидать, в результате применения операци

онного метода задача об интегрировании дифференциального

уравнения (9.1) с частными производными сведена к более простой

задаче интегрирования обыкновенного дифференциального урав

нения (9.6).

Общее решение обыкновенного линейного однородного диф

ференциального уравнения второго порядка с постоянными коэф

фициентами (9.6) имеет, как известно, такой вид:

где Л и В — постоянные величины, т.е. не зависящие от переменной

величины х, но они могут зависеть от параметра Эти коэффици

енты определим, используя условия (9.7) и (9.8).

На основании условия на бесконечности (9.7) из (9.9) получим:

(9.6)

(9.7)

АР = 0 прих —

(9.8)

^4* -VT*

Д P(x,s)=Ae +Ве

(9.9)

(9.10)

Соотношение (9.10) может быть выполнено только при следу

ющем условии:

Л = 0. (9.11)

Учитывая условие (9.11), подставим значение АР из равенства

(9.9) в (9.7):

— = В2а р* | е ~^Х dx = 2В а Р* V f",

откуда

____

2аР *у1х 'Is '

(9.12)

На основании равенств (9.11) и (9.12) из формулы (9.9) находим

окончательное выражение для изображения функции:

Л Р (Ху s) =

2G$*^fx 'Is

(9.13)

Для перехода от изображения к оригиналу следует совершить

обратное преобразование Лапласа. Воспользуемся известным об

ратным преобразованием Лапласа, которое приводится в соответ

ствующих таблицах — см., например, № 7 на стр. 483 [350], № 3.84

на стр. 153 [259],* № 51 на стр. 585 [427]:

-1

■yJT -I

- Уцх

4xt

(9.14)

где L'1 — символ обратного преобразования Лапласа, т.е.перехода

от изображения функции к ее оригиналу.

Учитывая формулу (9.14) и совершая в уравнении (9.13) обратное

преобразование Лапласа, получим:

Следует учитывать, что в справочнике [259] приводятся результаты преобразо

вания Карсона, отличающиеся лишь множителем от преобразования Лапласа.

Как и следовало ожидать, формула (9.15) совпадает с рассмот

ренным в главе 3 фундаментальным решением (3.28) для случая

мгновенного прямолинейного стока на плоскости в условиях

прямолинейно-параллельного потока.

Несколько изменим условие задачи — вместо мгновенного

рассмотрим непрерывно действующий сток с постоянным дебитом.

Т.е. предположим, что в начальный момент t- О прямолинейный

сток, изображающий на плоскости сечение прямолинейной галереи,

был включен с постоянным дебитом Qc, соответствующим участку

стенки галереи с площадью 2о (учитывается приток к галерее с

двух сторон). Тогда в математической постановке задачи равенства

(9.1), (9.2), (9.4) сохранятся, а вместо (9.3) граничное условие

примет такой вид:

(9.16)

Применим к уравнению (9.16) преобразование Лапласа:

(9.17)

Подставим в (9.17) решение (9.9), учитывая, что Л=0:

откуда

2 ok s Vs

(9.18)

и, следовательно, находим изображение АР из (9.9), (9.11) и (9.18):