Schlechta K. Nonmonotonic Logics: Basic Concepts, Results, and Techniques
Подождите немного. Документ загружается.


6.1. INHERITANCE DIAGRAMS
207
Diagram 6.28
r~j,
q~~ f~
shown in Diagram 6.28, so they are killed in the inner pipe.
The purpose of this construction is to satisfy the prerequisites of the Principle of
Disjunction.
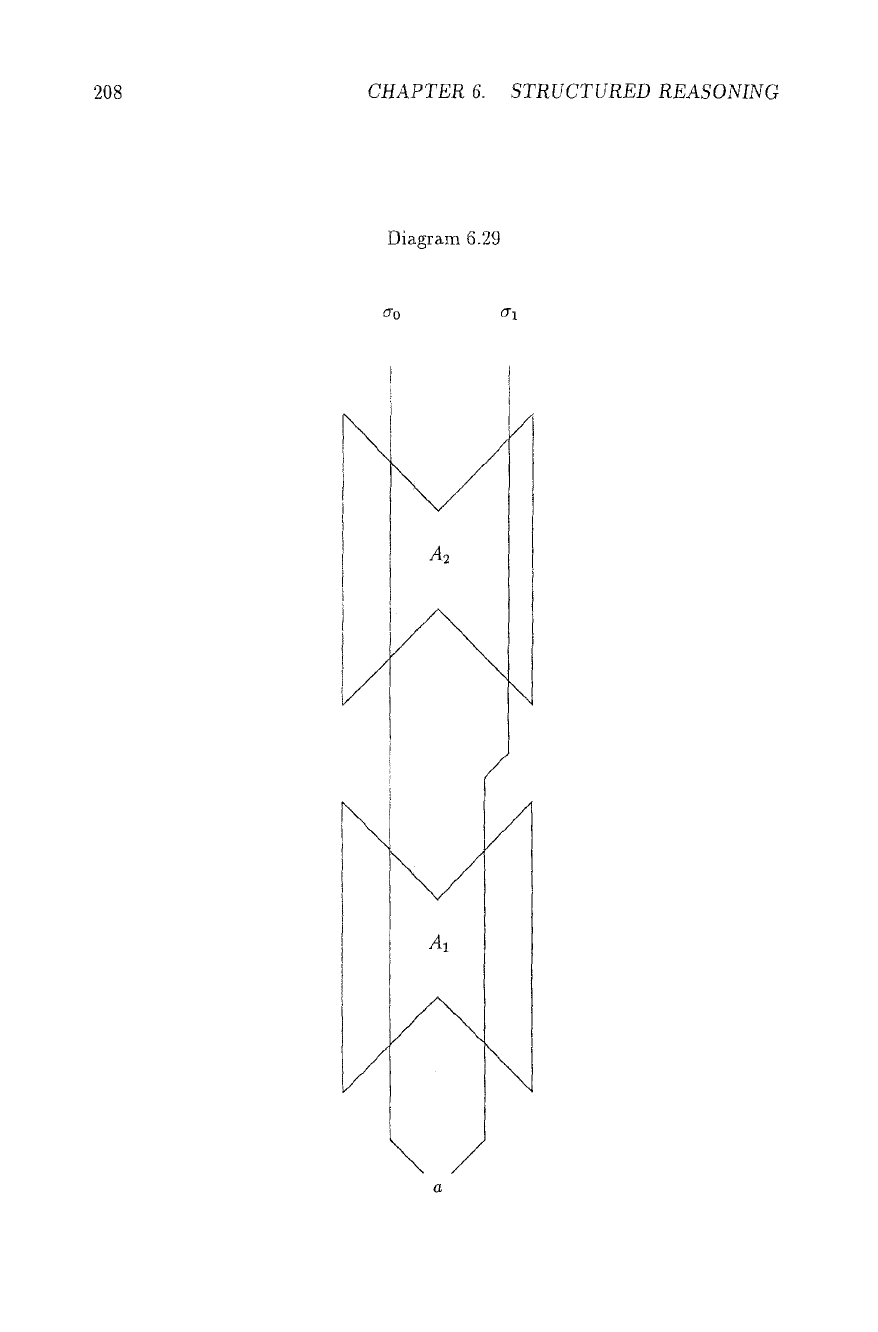
Combining Basic Cells (Diagram 6.29) The path a0 : a..- --* z0 will be
valid only in the extension where A1 and A2 are chosen positive, and 6h : a.-. --*
xl is valid iff A1 is positive, and A2 negative, thus oo encodes the extension
A1 A A2, ~1 the extension A1 A ~A2.
Final construction of P Let 2 ~ > t. Put n isomorphic Basic Cells/?i : i < n
with 2 n+l wings
Wi,j
: j < 2 ~+1 each "one above the other". (It will become clear
in a moment why we take 2 ~+1 wings instead of 2~.) For each of the 2 ~ different
extensions E we choose 2 wings in every cell to encode E (i.e. twice in the same
way) by joining the positive or negative pipes as shown above. Next, we join
all these paths in a bottom element a, and put a positive link ending in some x
on each path leaving the topmost cell. We thus construct 24+1 different paths
0 0 1 1 1
~j : a... --~ xj,
o" 3 : a-.. --* zi, j < 2 ~, where c~ and (rj are alike.
Formally, we first put the basic celIs
Bi : i < n
into F. For each ej : n -+ {0 =
1 Let
true, 1 = false}
(j < 2 '~) we construct two positive potential paths cr ~ crj.
a := 2j and work with the wings Wi,~, Wi,~+l in each cell Bi, making "vertical"
connections.
For i = O,
P
if 4i(0) = 0, add a --* p~,~ and a ~ Po,~+l,
if ed(0) = 1, add
a -+ Po,~
and
a --* Po,~+l.
Fori =n- 1,
if
r --
1) 0, add " 0 and 'p
1
~- rn_l, a ~ Xj
rn_l,a+ 1 ~
Xj,
if r 1) 1, add '~ _, 0 and r ~ 1
-- =
rn-l,a
"s -
v.-1,c~+I --4
Xj.
Fori<n-1,
208
CHAPTER 6. STRUCTURED REASONING
Diagram G.29
0~0 0" I
A2
\/
a

6.1. INHERITANCE DIAGRAMS
209
Diagram 6.30
53,j' ~,j,
4
if Cj(i) 0 and Cj(i + 1) 0, add r .p --+ p and
r p P
----- = ~,c~ Pi+l,a
i,a+l "--+ Pi+l,c~+l,
if
Cj(i)
0 and Cj(i + 1) 1, add re -+ ~ and r p
-=- =
,,a
Pi+l,~
i,a+l "--->
Pi+l,a+l,
P and ~ ~ P
if Cj(i) = 1 and
Cj(i +
l) = 0, add
ri, ~ --+ Pi+l,~ ri,~+l Pi+l,~+~,
if Cj(i) = 1 and
r +
1) = 1, add re -+ ~ and r '~ '~
,,c~ Pi+l,c~ i,a+l --+
Pi+l,c~+l"
From the discussion of the Basic Cells B~, it is clear that the following holds:
1) crj~ : a... --~ xj~ and c43 : a.-. -+ x~3 are valid (in the usual sense) positive paths
exactly in the extension which corresponds to Cj, i.e. makes a positive choice in
the core of Bi iff Cj (i) = 0.
2) all generalized paths from a to x] other than cr~ end in simple negative preclu-
sions.
We now show that all
~a,z}~, ~a,x},]]
for
j # jt
< 2 ~ are different, and we are
finished by 2 '~ > t =
the
number of truth values of 5". For this purpose, we add
for each pair < j, j/>, j # jl, j, jl < 2 ~, new nodes
bj,j,, blj,j,
and positive links
9 1 1 b/j,jt,
x~ -+ bj,j,
and
x~ -+ b/j,j,
for all k # 3, k < 2 ~ and the links
xj -+ bj,j,, xj~ --+
see Diagram 6.30.
Thus, in all extensions, and for all j, j/, there will be a path from a to
bj,j,,
because the "missing path" a ~ is replaced by its twin @, but not from a to
blj,j,,
as c~ and @ are true in the same extension, and the extension corresponding to
cr ~ has no valid path from a to
blj,j,.
As 5" is supposed to capture the intersection
of extensions, [[a,
bj,j,]J # ~a, bljJ.
By 1) and 2) above, our construction satisfies
the prerequisites of the Principle of Disjunction, so the pair
bj,jt, blj,j~
shows that
[[a,x}]] # [[a, x},]]. Repeating the argument, we see that all [[a, x}]], j < 2 ~ are
different, and we are done by 2 ~ > t. C3
It is natural to ask whether the finiteness assumption was necessary. Let me give
a short argument to show informally that it is. If we admit unboundedly many
truth values, we can encode for each potential path how it behaves with respect to
each decision (which corresponds essentially to a Nixon Diamond). Thus, roughly
speaking, a path will be in every extension iff every outcome of every decision is

210
CHAPTER 6. STRUCTURED REASONING
in its set of truth values. And there will be a valid path between two nodes, iff for
every outcome of every decision there is a path between the two, incorporating
this outcome as a truth value. Thus, looking at the (arbitrarily large) set of its
truth values, we can determine if a path is valid in every extension, and, looking
at the sets of truth values of each potential path linking two nodes z, y, we can
determine if there is a valid one in each extension.
Note: A preliminary version of this paper was presented at a German Workshop
on Nonmonotonic Reasoning held at Gesellschaft ffir Mathematik und Daten-
verarbeitung, Bonn, West Germany, in December 1989. The proceedings have
appeared as a technical report, see [Sch89-2].
6.1.6 A semantics for defeasible inheritance
Outline We use the technique o!' N-systems (see Chapter 3) to construct
models for (almost) any notion of validity in nets. (Though, in our opinion, the
extensions approach is best handled by a combination of these semantics and a
possible world technique.)
The first construction presented below has one defect: we build models from the
full theory, not from the axioms. To do the latter, we have to refine the method to
accomodate preclusion. The basic reason is, that direct links are for preclusion in
a stronger sense true than valid paths. We use N-families - decreasing sequences
of N'-systems - which give increasingly strong notions of truth and use them
to construct models suitable to express preclusion. The concept of X-families
is general enough to permit the construction of semantics for more complicated
notions of validity like the ones discussed in [Sch89-1].
Definition 6.41 Let g be a net, V(F) its vertices. We call V(F) the language
of F. A F-structure E is ~ tripel consisting of,. a universe, subsets of the universe,
denoted [[p~, for the p ~ V(F), and Y-systems over these subsets: E = < U,
{[[p]] : p C V(I')}, {N'(p) : p E V(F), N'(P) a N'-system over [[p~ } >.
We define validity:
g [~ p -+ q iff [[p~ O [[q~ 6 N'(p),
and say E is a ~-model of F (for ~ a notion of validity in nets), iff
forallp,q(El~ P-+qiffF ~p~q) and(E[~ p74qiffF ~p74q).
Proposition 6.42 Let F he a net and ~ be any notion of validity of links, which
1. does not permit P ~ p -~ q and F ~ p 74 q at the same time (note the
subsequent discussion, however),
2. satisfies P ~ p -~ p for all p.
Then there is a (canonical) ~-model ~ for ['.
Proof Let U := {f : V(F) --+ 2},
Xp
:= {f r U :
f(p)
= 1),
XH v := {f e
U : f(p)
= 0}
= U - Xv, Ip
:=
{q : F ~ p --+ q}, Ittp :~- {q : P ~ p 74 q},
s := {xp n xq : q e Ip} u n x,/q : q N(p) := {y c_ : ?z e

6.1. [NHERITANCE DIAGRAMS 211
Z;p.Z C Y}U{Xp}. We show that E := < U, {Xp: p E V(F)}, {N'(p): p E V(F))
> is a ~-model of 17': As 17' ~ p ~ p, so 17, ~ p 74 p, and p r I/IF. Again by 1.,
Ip N Ittp = ~. Moreover, N'(p) is a H-system over Xp for all p E V(F), so E is a
F-structure.
We turn to validity. 17, ~p--+ q => q E Ip => XpnXq EN'(p) => EI~ P---* q.
17, ~ p 7/+ q :ee q E Ittp => Xp ['l Xr = Xp - Xq E N'(p) => E I~ P 7 # q"
E I~ P --+ q ~ Xp N Xq E A/'(p). There are three cases to consider.
Case 1: Xp n X~ = X,, then p = q, and we are done by 2.
Case 2: There is Z E s Z C_ Xp N Xq.
Case 2.1: Z = Xp ~-1Xll~ C_ Xp M Xq for some r E Iltp.
The function
1 ifx=p
f(x) := 0 otherwise
is in Xp ;-t Xtt, and shows that q = p, and we are done again.
Case 2.2: Z = X v M X~ _C Xp N Xq for some r
E I v.
The function
1 ifx=porx=r
f(x) := 0 otherwise
shows that either q = p again or r -= q, thus q EIp and 17, ~ p --+ q by definition.
E I~ P 7# q =:> Xv - Xq = Xp M Xtlq E N'(p). Again we examine the above three
cases.
Case 1: Xp M XIIq = X v can't be.
Case 2.1: Z = Xp M X~ __ X v M XI/q is impossible too, as f = constant 1 shows.
Case 2.2: Z = Xp r3 Xtl~ C Xp M X1fq for some r E IIIp.
The function
0 ifx=r
f(x) := 1 otherwise
shows that q = r, so q E Iltp and 17' ~ p 7# q. []
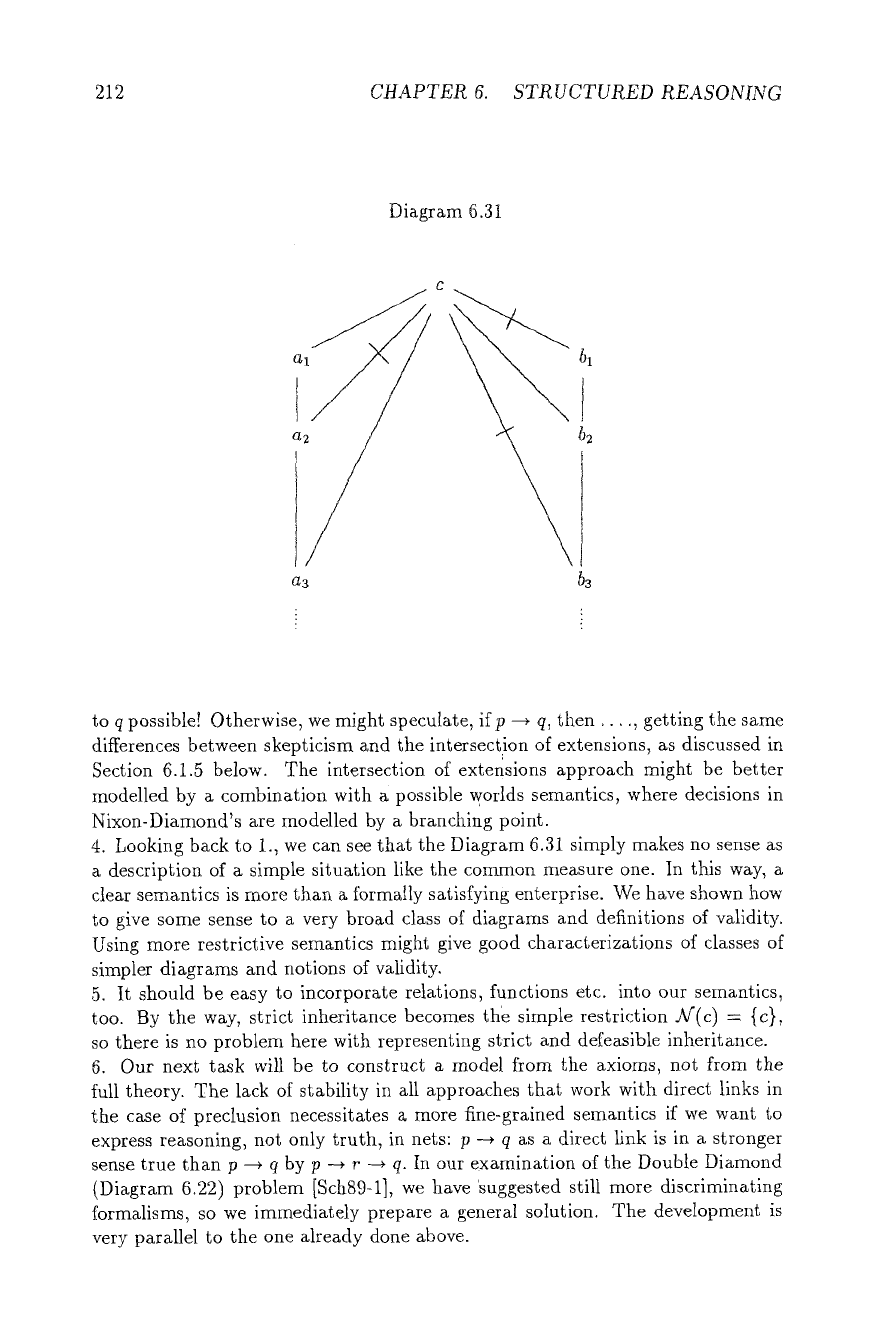
Discussion 1. We first tried simpler approaches like subsets of the real plane
and measures. But look at Diagram 6.31.
Following the simpler interpretation, we have to read: Most of al is in c, most
of a2 is in al, most of a2 is not in c. So, a2 has to be a lot smaller than al is
etc. In the end, some ai is very much smaller than b~ (or some bi than
al).
But,
then most of bl is in the complement of ai, and'we would have a negative arrow
from bl to ai, which simply is not there. If we took a lot of different models
and intersections of true statements, we could easily run into situations like those
discussed in Section 6.1.5, and be unable to fully model a skeptical approach. So,
taking different measures (N'(p)) for different p!s in V(F) seems ne<essary.
2. To represent directly contradictory information like the Garbage In Rule of
Thomason, we can construct 2 models in the above way, much as his construction
for the 4-valued monotonic case.
9 3. We have a ,3-valued semantics: [[p~ A [[q]] E Af(p), [[p]] - [[q~ E X(p) and
neither. We would like to emphasize very strongly that the latter case is not
intended to express lack of intbrmation: There simply is no decision with respect
212
CHAPTER 6. STRUCTURED REASONfNG
Diagram 6.31
C
I
a2
aa b3
to q possible! Otherwise, we might speculate, ifp ---+ q, then .... , getting the same
differences between skepticism and the intersection of extensions, as discussed in
Section 6.1.8 below. The intersection of extensions approach might be better
modelled by a combination with a possible worlds semantics, where decisions in
Nixon-Diamond's are modelled by a branching point.
4. Looking back to 1., we can see that the Diagram 6.al simply makes no sense as
a description of a simple situation like the common measure one. In this way, a
clear semantics is more than a formally satisfying enterprise. We have shown how
to give some sense to a very broad class of diagrams and definitions of validity.
Using more restrictive semantics might give good characterizations of classes of
simpler diagrams and notions of validity.
5. It should be easy to incorporate relations, functions etc. into our semantics,
too. By the way, strict inheritance becomes the simple restriction N'(c) = {c},
so there is no problem here with representing strict and defeasible inheritance.
6. Our next task will be to construct a model t?om the axioms, not from the
full theory. The lack of stability in all approaches that work with direct links in
the case of preclusion necessitates a more fine-grained semantics if we want to
express reasoning, not only truth, in nets: p --+ q as a direct link is in a stronger
sense true than p ~ q by p --~ r -4 q. In our examination of the Double Diamond
(Diagram 6.22) problem [Sch89-1], we have suggested still more discriminating
formalisms, so we immediately prepare a general solution. The development is
very parallel to the one already done above.

6.1. INHERITANCE DIA GRA MS 213
Lemma 6.43 Let < s " i < 3" >,
s C
IP(X) be such that A,B E U{gk : k < 7}
ArqB r 0. Then Hi(X) := {A C X: 3B E U{s i _<j < 3'}..B C A} U {X}
for i < 3' is a N'-family over X. []
Example 6.1 Let a be any ordinal, U := {f~: c~ ---+ 2}. For i < c~ let Xi :=
{f E U : f(i) = 1}, X/ti := {f E U : f(i) = 0} = U-Xi. For j < ~, i < 3'
let [j,i, I/lj,i
C_
ct, j r f/lj,i,
(U{fj,i :
i < 3'})
gl
(U{lltj,i
:
i < 3'}) = (i Let s :=
n xk : k u {xj n
x,,k : c mj,d.
Then < s : i < 3' > satisfies the prerequisites of Lemma 6.43 for all Xj, j < c~.
Thus, for all j, Afj,i(Xj) := {A C Xj: ~B E U{gj,* : i < k < 3'}./3 C A}
U
{Xj}
is a H-family of length 3' over Xj.
Definition 6.44 A F, 3'-structure E is a tripel, consisting of a universe, subsets
of the universe for all p E V(F), and a N-family of length 7 over these subsets:
= < U, {[[p]] : p E V(F)}, {< H/(p): i < 3` >: p E V(F),< Y/(p): i < 7 > a
A/'-family
over
[[p]] ) >.
We define 3` degrees of validity: Let i < 7, then ~ I~ ~P ~ q iff [[p~ N [[q]] E AYe(p)
and E I~ iP 74 q iff [[p]] - [[q~ E Af/(p) and say for a notion ~:=<~i: i < 3' >
of validity in nets of 7 degrees that 2 is a ~-model of F iff E is a F, 3'-structure
and for all p, q E V(F), i < 7:
~ ]~ ~p --~ q iff F ~ p -4 q and E i,~ ~p 74 q iff r ~ p ~C~ q.
Proposition 6.45 Let F be a net asld ~=<~i: i < 3` > a notion of validity of
links, which
1. does not permit F ~ p --* q, r ~j p 7~ q for any p, q, i, j at the same time,
2. satisfies I" ~ p --+ p for all p, i,
3. is increasing, i.e. satisfies r ~; p --* q ~ P ~j p --+ q for all p, q, i > j (likewise
for negative links).
Then there is a (canonical) ~-modeI for P.
Proof We can follow almost verbatim the construction and proof of Proposition
6.42. []
We now have the tools to handle preclusion, again with the proviso that no p --~ q,
p 7z~ q E r simultaneously. But this is an inessential restriction, as we can again
develop two models in tandem.
We extend I~ i to handle paths too. This, along with the notion of a preclusion-
structure, is made precise in
Definition 6.46 Set 3' := 2, w := 0, s := 1 (w for weak, s for strong). Let E be
a F, 2- structure. We say E is a F, 2,p-structure (p for preclusion), iff it satisfies
b. E I~ t~cr e* Z I~ ~ a+ where c ~+ is the "shortcut of a," i.e. treating ~r as a
single arrow,
c. ~ [~ ~, o = xl... z,~z iff
0. I>

214
CHAPTER 6. STRUCTURED REASONING
1. For noi<n, El~
~xig, and there is no r
=xl...yl...yr~...xiwithEl~ wr
and E ~ sykg,
2. if there is r = xi...y, E I~ ~r, E f~ ~Y~, then xl...yg is precluded (here,
we mean of course the semantical counterpart, i.e. the negation of 1).
(The negative arrows are handled entirely symmetrically.)
It is trivial to see that a P, 2,p-structure such that E l~ ,P --+ q iff p --+ q E F is
a correct model of the sceptical notion of inheritance.
Resume We have constructed a 5-valued model which gives E ]~ ~p -+ q iff
F ~:p~q, crnot adirect link, and ~1~ ~P--+qiffP--+ q E P. So, strong
validity corresponds to direct links, weak validity corresponds to valid paths (resp.
their result), this distinction makes it possible to handle preclusion.
6.2 Networks of inference - J. Pearl's book
6.2.1
Introduction
This Section deals with - probabilistic and more general - independence in graphs
representing influence relations. As independence permits local computation, it
is of high interest for questions of complexity.
More motivating discussion can be found in Pearl's book, this Section is largely
a service to the reader of [Pea88], and illustrates the handling of independence in
other contexts than the logical one (see Section 1.3.11).
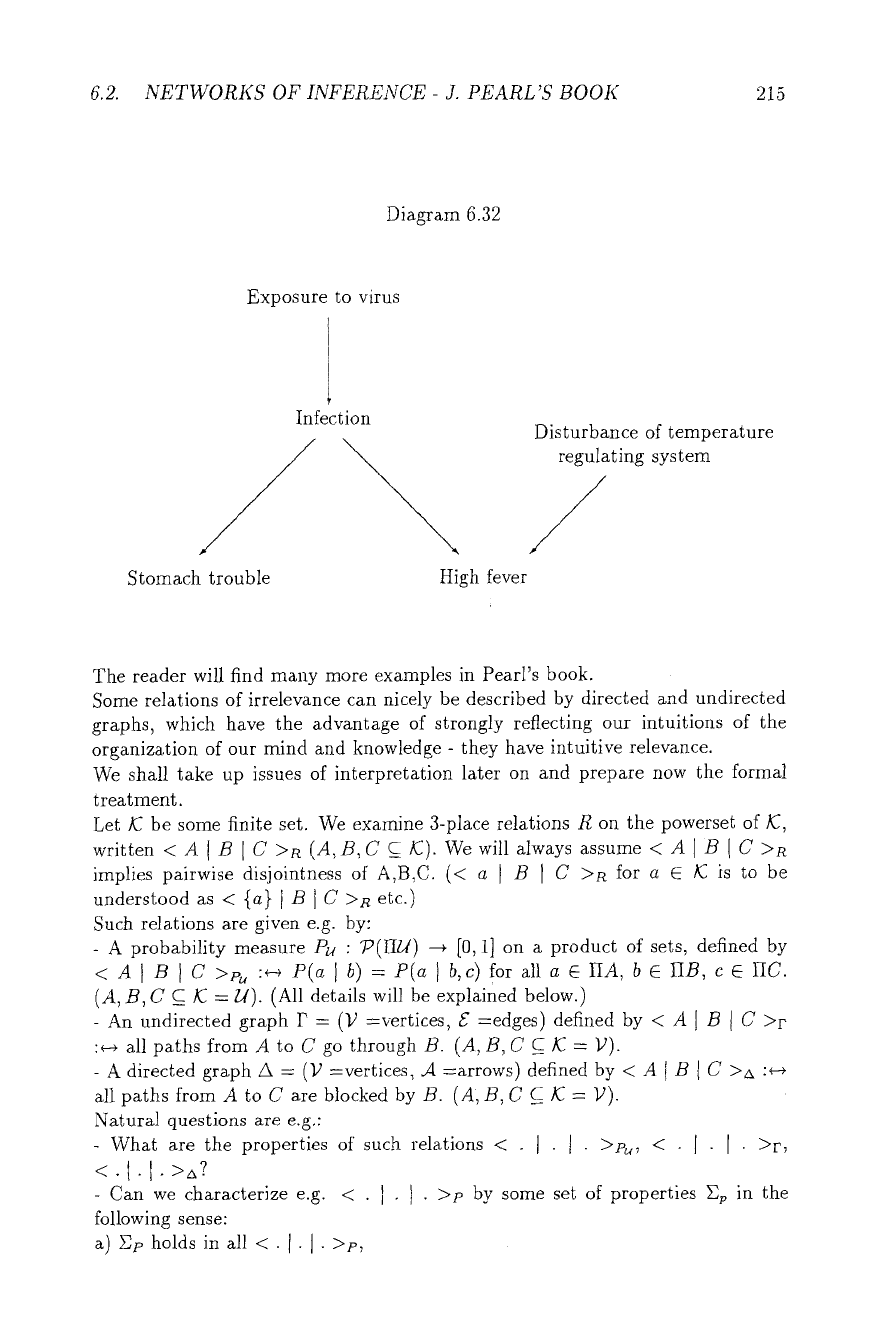
Let us give an illustration of possibilities of independence and influence. Suppose
we are given the following Diagram 6.32, where arrows stand for (probabilistic)
causal relations, i.e. the cause will usually bring the effect about, but not always.
The diagram is supposed to capture some part of medical knowledge.
Suppose now we know that person z has been exposed to the virus. So we will
suspect him to develop fever and stomach trouble in some days. Suppose now
that we
know
that an infection has or has actuMly not taken place, then our
knowledge of the exposure will be irrelevant for our conclusion about fever and
trouble. Thus, the knowledge about the actual infection has made the knowledge
about the exposure irrelevant~
Suppose now we know that person x has high fever. Then we will - to a certain
degree - consider it probable that he also has stomach trouble. If we are how-
ever informed again about the actual infection, the knowledge about high fever
will become irrelevant. (Leaving aside such intermediate knowledge as general
development of symptoms.) We have a similar situation as above.
Suppose on the other hand, that we know nothing about x's fever or troubles then
we might consider both diseases - i.e. infection and disturbance - independent. If
we are now informed that x has high fever, then the information that he has no
infection will influence our hypothesis about his temperature system. So, opposite
to the above cases, knowledge about a common consequence makes formerly
independent causes dependent.
6.2. NETWORKS OF INFERENCE - J. PEARL'S BOOK
215
Diagram 6.32
Exposure to virus
1
i
L
Infection
Stomach trouble
Disturbance of temperature
regulating system
/
High fever
The reader will find many more examples in Pearl's book.
Some relations of irrelevance can nicely be described by directed and undirected
graphs, which have the advantage of strongly reflecting our intuitions of the
organization of our mind and knowledge - they have intuitive relevance.
We shall take up issues of interpretation later on and prepare now the formal
treatment.
Let K be some finite set. We examine 3-place relations R on the powerset of K,
written < A I B [ C >R (A,B,C c K). We will always assume <
A IB I C >R
implies pairwise disjointness of A,B,C. (< a I B I C >R for a E ~ is to be
understood as < {a} t B1 C >R etc.)
Such relations are given e.g. by:
-
A probability measure
Pu
: ~(1]N) ~ [0, 1] on a product of sets, defined by
< A I B I C >pu :*-* P(a I b) = .P(a I b,c)
for all a E HA, b E liB, c E IIC.
(A, B, 6' _ K = N). (All details will be explained below.)
- An undirected graph P = (12 =vertices, g =edges) defined by < A B I C >r
:~ all paths from A to C go through B. (A, B, 6, C ]C = P).
- A directed graph A = (F --vertices, ..4 =arrows) defined by < A I B C >~x :~
all paths from A to C are blo&ed by B. (A, B, C C~ K: = F).
Natural questions are e.g.:
What are the properties of such relations < . [ 9 I 9
>Pu,
< 9 [ 9 >r,
<-t-l->~?
-
Can we characterize e.g. < 9 I - I . >P by some set of properties Ep in the
following sense:
a) 2p holds in all < . I. J- >P,

216
CHAPTER 6. STRUCTURED REASONING
b) if K; is any set, R a 3-place relation on P(~), and R satisfies Gp, is there then
/2 and a probability measure
Pu
: 5~ --+ [0, 1] and a bijection f : K~ --~/2 such
that <
A IB [ C >R +-+ < f[A] ] f[B] l f[C ]
>pu?
We shall henceforth assume X to be finite, and E = W(X). P on E will also be
said to be on X, and also called a probability variable. P is called strictly positive
iif
P(A)
= 0 ~ A = (~. For x E X, we shall also write P(x) for P({x}). Moreover,
the notation P : X -+ [0, 1] is justified, as E is fixed by X, and P(Y) for Y C_C_ X
is determined by the values on the singletons - as any Y C_ X is countable, even
finite, and by b. above.
Fact 6.47 Let Xi : i < n (n < co) be finite sets, P~ :
X; -+
[0, 1] probability
measures, then there is a (unique) probability measure P : [I{Xi : i < n} --+ [0, 1]
on the product defined by P(a0...x~-l):= P(< z0...x~-I >) :=
Po(xo) *... *
Conversely, if a probability measure P : II{Xi : i < n} --~ [0, 1] is given, m C__ n,
m = {j,...jk}, then P~(xj~ ...zjk ) := 2{P(xjl
...zj~x~l...z~,): z~ < X~,i,.
n - m} (suitably reordered) defines a probability measure on 11{& : j Em}.
We shall abuse notation by writing P for P~ too - the context will disambiguate.
In particular, for P :
XzY -~
[0, 1],
x E X, y E Y, P(z I Y)
will mean
pyre) =
PI~,~) P(~,_l
P({<xt,y>:xtEX-~ = ~{P(xt,y):xtEX}
Definition 6.48 Let X, Y etc. be variables.
a) Expressions like
P(X I Y) = P(X I Y, Z)
are to be understood as universally
quantified, i.e. Vx E
fiX, y C 1-IY, z E UZ.P(x l Y) = P(x l Y, z).
b) By P[X] we mean {<
:c',P(x)
>: z E IIX}, likewise
P[X I Y]
:= {<
x,y,P(x ]
y) >: x r
IIX, y
E UY}, etc.
c) Likewise, for X = {X~...X~} a set of variables,
P[X]
is to be read
PiXy,...,
X~] etc.
In Section 6.2.2, various independence relations are discussed (this is material
fl'om Chapter 3 of [Pea88]): in Section 6.2.2.1 those defined from probability
measures, in Section 6.2.2.2 independence defined by undirected graphs, and in
Section 6.2.2.3 independence as given by directed acyclic graphs (causal net-
works). In Section 6.2.3 we go into the details of computing probability functions
in directed acyclic graphs: The task is - essentially - to compute a probability
measure on the product of the vertices from tocal conditional probabilities be-
tween parents and children in the graph, using the independence relations given
by the graph. (The prerequisites and the result are made precise before Lemma
6.63 and in Corollary 6.64.) More precisely, we are interested in computing the
conditional probability
P(x I e),
where z is a value on some node X, and e is a set
of values on a set of nodes E. In the rest of Section 6.2.3, we reconstruct Pearl's
method (Chapter 4 in [Pea88]) of computing
P(x
I e) in singly connected directed
acyclic graphs by local computations and message passing. The situation is made
precise before Definition 6.65, and the results are summarized following Lemma
6.71.
