Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

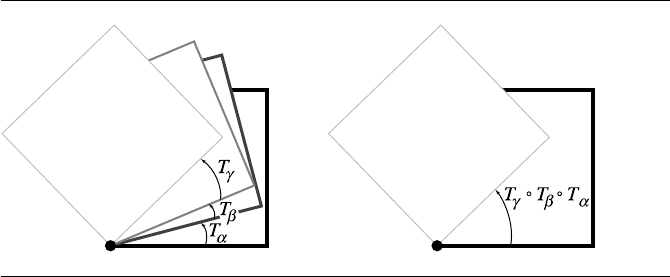
104 Chapter 3 Vector Algebra

Figure 3.40 Composition of afﬁne maps (rotation).

3.5 Barycentric Coordinates and Simplexes

We saw that the coordinates of points in an afﬁne space can be deﬁned in terms of the

basis vectors of the underlying vector space, relative to the point O of F:

Q =u + O

= a

v

+ a

v

+···+a

v

+ O

An alternative is to use what we might call “basis points”: P

=O, P

=O +v

, P

O +v

, ..., P

= O +v

(that is, a set of points consisting of O and the points

generated by adding the basis vectors to O).

We can then represent a point Q ∈ A,relativetoF as

Q = P



1 − a

− a

−···−a



+ P

+···+P

Q = P

+ P

+···+P

where a

is deﬁned by

1 = a

+ a

+···+a

This last identity is particularly important—the coefﬁcients sum to 1.

This should be recognizable as an afﬁne combination, and the values a

, ..., a

are called the barycentric coordinates of Q with respect to F. Figure 3.41

shows both the standard frame coordinates and the barycentric coordinates.

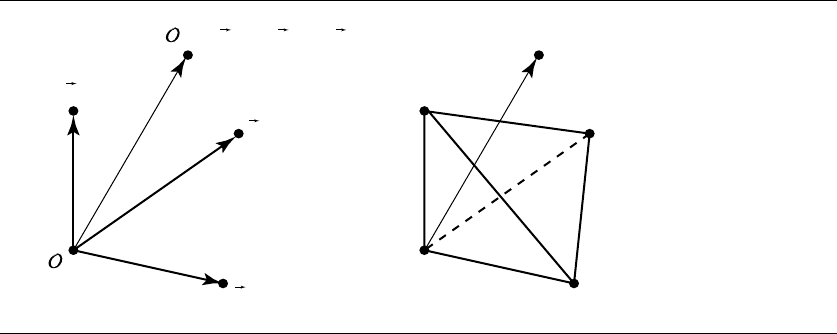
3.5 Barycentric Coordinates and Simplexes 105

Q = a

+ a

Q = + a

+ a

(a) (b)

Figure 3.41 Afﬁne (a) and barycentric (b) coordinates.

You might expect, due to the fundamental relationship between points and vec-

tors in an afﬁne space, that vectors themselves can also be represented using barycen-

tric coordinates; this is indeed the case. Recall that we can write any vector as

u = a

v

+ a

v

+···+a

v

If we let a

=−



+ a

+···+a



, then we can rewrite the vector as

u = a

+ a

+···+a

Note that

+ a

+···+a

=−



+ a

+···+a



+ a

+···+a

= 0

That is, the coefﬁcients sum to 0, not 1 as we have for points. The “basis points” are

generallyreferredtoasasimplex, just as the distinguished point plus basis vectors are

called a frame.

An afﬁne map’s preservation of relative ratios applies to barycentric coordinates

for higher-order simplexes as well as to lines (see Section 3.4). Let’s take this reasoning

a step further. A basis point K of a simplex is simply that point for which the barycen-

tric coordinates are of the form



= 0, a

= 0, ..., a

= 1, ..., a

= 0



. So, if the

basis points are transformed, we get another set of basis points deﬁning another sim-

plex, afﬁne combinations of which are equivalent to points to which the afﬁne map

has been applied. So, an afﬁne map can be completely and uniquely described by its

operation on a simplex. However, it turns out that an afﬁne map is even more general

106 Chapter 3 Vector Algebra

than that. It may transform an n-simplex into a set of n points that is not a simplex;

this is what happens when the map is a projection.

3.5.1 Barycentric Coordinates and Subspaces

Just as we can have subspaces of linear (vector) spaces, so too can we have afﬁne sub-

spaces, and barycentric coordinates can be discussed in terms of these. Suppose we

have an n-dimensional afﬁne space A as deﬁned by a simplex S =



, P

, ..., P



We can then deﬁne an m-dimensional subspace B ⊂ A, as speciﬁed by a simplex

T =



, Q

, ..., Q



. Any point R ∈B can be represented as

R = b

+ b

+···+b

with the usual deﬁnition of 1 = b

+ b

+···+b

. Of course, since the Q

are

representable in terms of A, we could rewrite R in terms of B.

Each n-simplex is composed of n + 1 points, so a 1-simplex is a line segment, a

2-simplex is a triangle (deﬁning a plane), and a 3-simplex is a tetrahedron (deﬁn-

ing a volume), as shown in Figure 3.42. This ﬁgure also illustrates the relationship

between barycentric and frame coordinates. Consider the 2-simplex in the middle

of the ﬁgure: the point R can be deﬁned as described above in terms of barycentric

coordinates; however, emanating from Q

is a line segment that intersects the oppo-

site side of the simplex at a point c



− Q



(and similarly for the other two basis

points), and we can consider any of the Q

to be O and the vectors from that point

to its two neighbors as deﬁning an afﬁne frame. It’s particularly interesting to note

that any two of these interior, intersecting line segments are sufﬁcient to determine

R. This also suggests that only two of the simplicial coefﬁcients are sufﬁcient to spec-

ify a point; the reason this “works” is due to the fact that these coefﬁcients sum to 1,

and so if we know two coefﬁcients, the third value is implied.

3.5.2 Afﬁne Independence

For an afﬁne frame, the basis vectors must be linearly independent. Considering that

an afﬁne frame or simplex can be used to deﬁne an afﬁne space, it’s logical to assume

there’s an analogous independence criterion for simplexes.

Recall that linear independence of vectors means that none of them are parallel.

Intuitively, the analogous characteristic for basis points is that none of them are

coincident, and that no more than two are collinear. That is, none are an afﬁne

combination of the others. Formally, we can say that a set of basis points are afﬁnely

independent if their simplicial coordinates are linearly independent (in the same way

that vectors in a vector space are linearly independent).

Let P

, P

, ..., P

be the n + 1 points deﬁning an n-simplex, and v

= P

− P

(recall that we’re using the convention that P

=O). If the n vectors v

, v

, ..., v

are

linearly independent, then the points P

, P

, ..., P

are afﬁnely independent. This

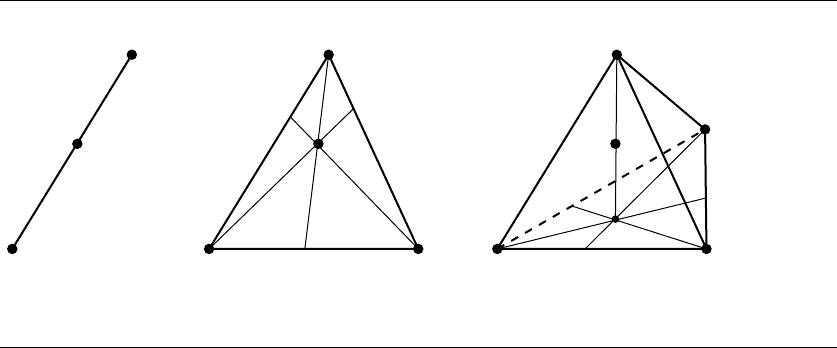
3.5 Barycentric Coordinates and Simplexes 107

(a)

(b)

(c)

Figure 3.42 The ﬁrst three simplexes: a line (a), a triangle (b), and a tetrahedron (c).

can be observed by looking at Figure 3.42: the two points deﬁning the 1-simplex can-

not be coincident; the three points deﬁning the 2-simplex cannot be all collinear; the

four points deﬁning the 3-simplex cannot be all coplanar. Note that if we “degen-

erate” any of these simplexes in that way, we get a space whose dimension is 1 less,

which corresponds to the “next smallest” simplex.

Chapter

4Matrices, Vector

Algebra, and

Transformations

4.1 Introduction

The point of the preceding chapter was to introduce the concepts and principles

of geometry in a coordinate-free fashion. For example, most treatments of the dot

product simply describe it in terms of how you perform arithmetic on row and

column matrices, without providing much in the way of an intuitive understanding

or justiﬁcation, whereas our approach was purely geometrical.

DeRose (1989,1992) and Goldman (1985, 1987) strongly advocate this

coordinate-free approach. DeRose describes a coordinate-free API, and an imple-

mentation is available. Such an approach has much to recommend it, especially in

contrast to the more usual scheme of requiring programmers to explicitly multiply

matrices, invert them, generally keep track of “what space they’re in,” and perform

all operations on coordinates.

On the other hand, the reality is that most graphics software is not so constructed,

and the programmer needs to deal with matrices and operations on them; further,

even a coordinate-free library would likely involve matrices in its implementation.

The goal of this chapter is to bring together the concepts and techniques intro-

duced in the previous chapter and the matrices introduced in the chapter before

that.

In Chapter 2 we covered matrices as a rather abstract tool, rather divorced from

their relationship to the vector algebra described in Chapter 3. However, we’ve

109

110 Chapter 4 Matrices, Vector Algebra, and Transformations

dropped a few clues along the way, such as our calling 1 × n matrices“rowvectors,”

or discussing coordinates in the context of afﬁne transformations; readers who have

been taught about transformations, spaces, and matrices would have seen this as

rather obvious, and readers for whom this sort of presentation of the topics is new

were probably making the connections as well.

Now, we bring together all these concepts and show explicitly how matrices are

used to represent points, vectors, and transformations, but from the point of view

of the “vector algebra” approach. This differs from the more typical treatment as

found, for example, in Rogers and Adams (1990) or Newman and Sproull (1979),

which generally start off by describing points and vectors in terms of x-, y-, and

z-coordinates, dot products as unintuitive and seemingly arbitrary operations on

the coordinates, and transformations as multiplications of magically constructed

matrices multiplied by the coordinates of a point or vector.

4.2 Matrix Representation of Points and

Vectors

In Section 3.3.3, we showed that an afﬁne frame F can be represented as a set of basis

vectors and an origin

F =



v

, v

, ..., v

, O



that any u ∈ V ,whereV is a vector space, can be written as

u = a

v

+ a

v

+···+a

v

(4.1)

and that any point P ∈ P (the set of points related to the associated vector space for

the frame) can be expressed as

P = a

v

+ a

v

+···+a

v

+ O (4.2)

Recall that the Coordinate Axiom deﬁned in Section 3.3 says that a point mul-

tiplied by 0 yields the zero vector, so we can write 0 · O =



0. If we also recall the

deﬁnition of tuple multiplication (Section 2.3.4) and the matrix notation associated

with it, we can rewrite Equation 4.1 in matrix notation:

4.2 Matrix Representation of Points and Vectors 111

u = a

v

+ a

v

+···+a

v

= a

v

+ a

v

+···+a

v

+ (0 ·O)

[

... a

][

v

... v

]

[

··· a

]







v







[

··· a

]







1,1

1,2

··· v

1,n

2,1

2,2

··· v

2,n

n,1

n,2

··· v

n,n

··· O







(4.3)

So, we can represent a vector as a row matrix whose ﬁrst n elements are the coefﬁ-

cients of the afﬁne coordinates and whose last element is 0. If the afﬁne frame is clear

from context, we will use the shorthand notation u = [

··· a

]. Be

aware that this notation is for convenience in identifying a vector u and its representa-

tion in the frame, but the equality is really in the sense of that shown in Equation 4.3.

We can apply the same argument for points. Again invoking the Coordinate

Axiom, we can rewrite Equation 4.2 in matrix notation:

P = a

v

+ a

v

+···+a

v

+ O

= a

v

+ a

v

+···+a

v

+ (1 · O)

[

... a

][

v

... v

]

[

··· a

]







v







[

··· a

]







1,1

1,2

··· v

1,n

2,1

2,2

··· v

2,n

n,1

n,2

··· v

n,n

··· O







(4.4)

112 Chapter 4 Matrices, Vector Algebra, and Transformations

So, we can represent a point as a row matrix whose ﬁrst n elements are the coefﬁcients

of the afﬁne coordinates and whose last element is 1. If the afﬁne frame is clear from

context, we will use the shorthand notation P = [

··· a

]. Be aware

that this notation is for convenience in identifying a point P and its representation

in the frame, but the equality is really in the sense of that shown in Equation 4.4.

Of course, the basis vectors and origin for an afﬁne frame F are no different than

any other vectors and points in an afﬁne space, and so we can rewrite the matrix

representing them as







1,1

1,2

··· v

1,n

2,1

2,2

··· v

2,n

n,1

n,2

··· v

n,n

··· O







(4.5)

which is, as you can see, a square (n + 1) × (n + 1) matrix. This will come in handy,

as you’ll see in the subsequent discussions.

Readers who have had any sort of experience programming two- or three-

dimensional graphics applications may well be objecting at this point that you typ-

ically use only the coordinates to represent a point or vector. A bit of explanation

is in order: Typically, representations of individual objects and entire scenes are im-

plemented as some sort of hierarchy. Parts of, say, a car are grouped, and each part

consists of subparts, and so on. Subparts are often deﬁned in their own “local” frame,

which is then transformed into the space of its “parent,” which itself is transformed

into the space of its parent, and so on upward in the hierarchy toward the root, which

isgenerallydeﬁnedtobein“worldspace.”

At each level, there is a local frame. This frame has as its origin the point

[

001

]or [

0001

], depending on whether it’s a two-dimensional or three-

dimensional system, respectively. Further, the frame has as its set of basis vectors what

isreferredtoastheusual basis (or more formally, the standard Euclidean basis). The

basis is orthonormal, follows the right-hand rule, and is ordered as follows: vector v

hasa1intheith position and 0 elsewhere. Conventionally, these are called the x-, y-

, and z-axes, respectively. The coefﬁcients of a point or vector—its coordinates—are

also referred to as the x-, y-, and z-components, respectively. Thus, the matrix seen

in Equation 4.5 is, in a three-dimensional system,







1000

0100

0010

0001







4.3 Addition, Subtraction, and Multiplication 113

and similarly for two-dimensional systems. Obviously, these are just identity matri-

ces, and so we can write the last line of Equation 4.4 as simply

P =

[

··· a

]

It was shown in Section 2.9.2 that we can construct an orthonormal basis from

any other (linearly independent) basis; thus, we can conventionally use these usual

bases for all local frames (“coordinate systems”), with no loss of representational

power. The usual bases have obvious advantages in terms of intuitive appeal and

computation. The rest of this chapter assumes the use of usual bases.

4.3 Addition, Subtraction, and Multiplication

In Section 4.2, we showed how points and vectors were represented in matrix form.

Here, we show formally how addition, subtraction, and scalar multiplication of

points and/or vectors are deﬁned in terms of their coordinate/matrix representation.

In all our previous discussions of afﬁne spaces, we’ve been (intentionally) quite

general: basis vectors have been given names like u, v, and so on, and their coor-

dinates been given names like a

, a

, and so on. By convention, in two- and three-

dimensional space, the basis vectors are generally referred to as the x-, y-, and z-axes,

and the coordinates are generally referred to directly as the x-, y-, and z coordinates.

However, to avoid confusion in the following sections, we’re going to refer to the ba-

sis vectors using a convention, often observed in calculus texts, which calls the basis

vectors i, j , and k. We’ll call the origin O as before (Figures 4.1 and 4.2 show this

notation).

4.3.1 Vector Addition and Subtraction

Suppose we have two vectors u = u

ı +u

 + u



k and v =v

ı +v

 + v



k, and we

wish to add or subtract them in their matrix representations:

u +v =

[

]

[

]

= u

ı +u

 + u



k + v

ı +v

 + v



= (u

+ v

)ı + (u

+ v

)  + (u

+ v

)



[

+ v

]

The proof for subtraction is analogous.