Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

154 Chapter 4 Matrices, Vector Algebra, and Transformations

T(P)

T(v ) T(v )

T(v )

T(v)

Figure 4.22 Mirror image in 3D.

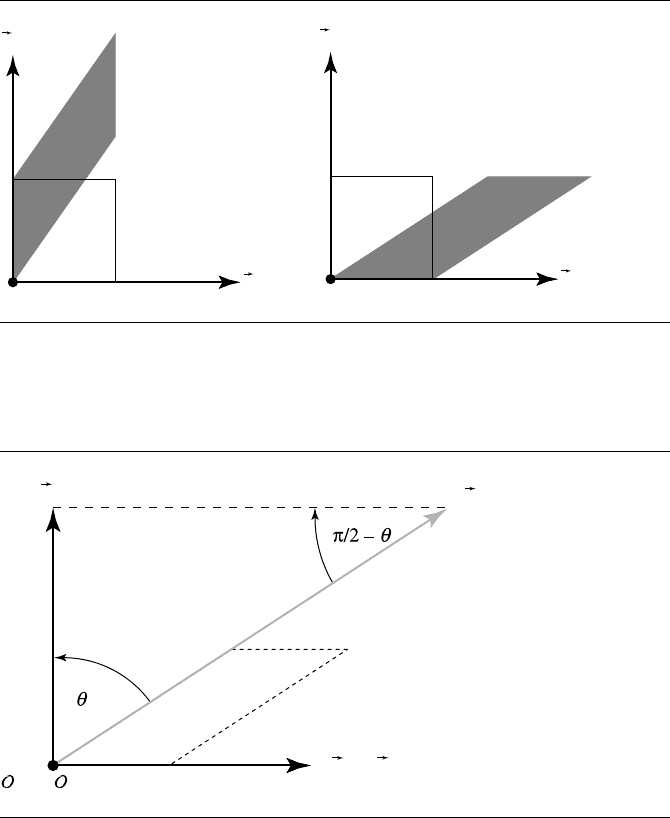
Simple Shearing

Shearing, in general, may be done along any line (in 2D) or orthogonally to any plane

(in 3D), but as with the other transforms, we’ll discuss the simple cases ﬁrst. The sim-

ple shears are done along the basis vectors and through the origin. Shears, as can be

seen in Figure 4.23, transform rectangles into parallelograms; these parallelograms,

however, must have the same area as the original rectangle. As any parallelogram has

its area as base × height, it should be clear why the simple shears preserve either the

base or height of an axis-aligned rectangle.

There are numerous options for specifying a simple shear. The one we’ll use here

speciﬁes the axis along which the shearing takes place and the shearing angle; other

books, such as M

oller and Haines (1999), specify a shearing scale rather than an

angle.

Again we’ll construct a transformation matrix by considering in turn what the

transformation must do to the basis vectors and origin of our frame. We’ll show a

shear along the x-axis (the right-hand image in Figure 4.23); we’ll refer to this as T

xy,θ

(the reason for the subscript being xy rather than just x will be more clear when we

cover 3D shearing).

First, let’s consider the image of v

—the x-axis, under T

xy,θ

. As can be seen in

Figure 4.24, the x-axis remains unchanged:

xy,θ

(v

) =v

[

100

]

4.7 Vector Geometry of Afﬁne Transformations 155

Figure 4.23 Shearing in 2D.

T(v

) = v

T(v

)

= T( )

Figure 4.24 T

xy,θ

The image of v

—the y-axis, under T

xy,θ

—can be computed in the following

fashion: if we consider the right triangle formed by the origin O and the points

O +v

and O + T(v

), the angle whose vertex is at O is θ . If we recall that v

=1

(because we’re assuming standard Euclidean basis), we can use simple trigonometry

to deduce the image of v

under T

xy,θ

156 Chapter 4 Matrices, Vector Algebra, and Transformations

xy,θ

(v

) =

[

tan θ 10

]

Finally, T clearly has no effect on the origin O,sowehave

T(O) = O

[

001

]

and thus our transformation matrix is

xy,θ





T(v

)

T(v

)

T(O)









100

tan θ 10

001





A similar approach for T

yx,θ

(a shear in the y-direction) yields

yx,θ





1 tan θ 0

010

001





In three dimensions, there are six different shears. If we let

ηγ

= tan θ

ηγ

where η speciﬁes which coordinate is being changed by the shearing matrix and γ

speciﬁes which coordinate does the shearing, then the following schematic can be

constructed that shows the placement of the shearing factor to get the desired shear

direction:







1 H

0001







Only one of these H factors should be nonzero. The composition of two or more

shears must be implemented by forming each shear matrix and multiplying the ma-

trices together.

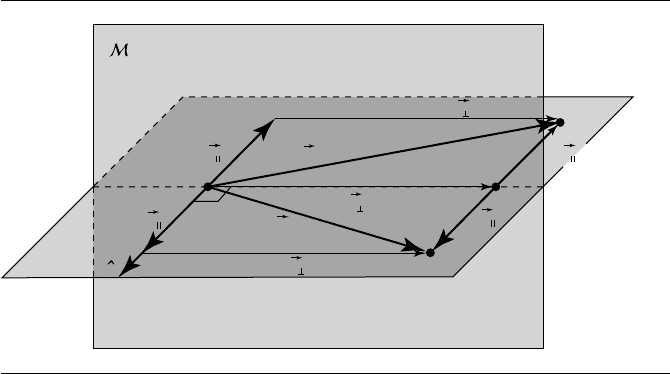
4.7 Vector Geometry of Afﬁne Transformations 157

ˆv

ˆn

Figure 4.25 General shear speciﬁcation.

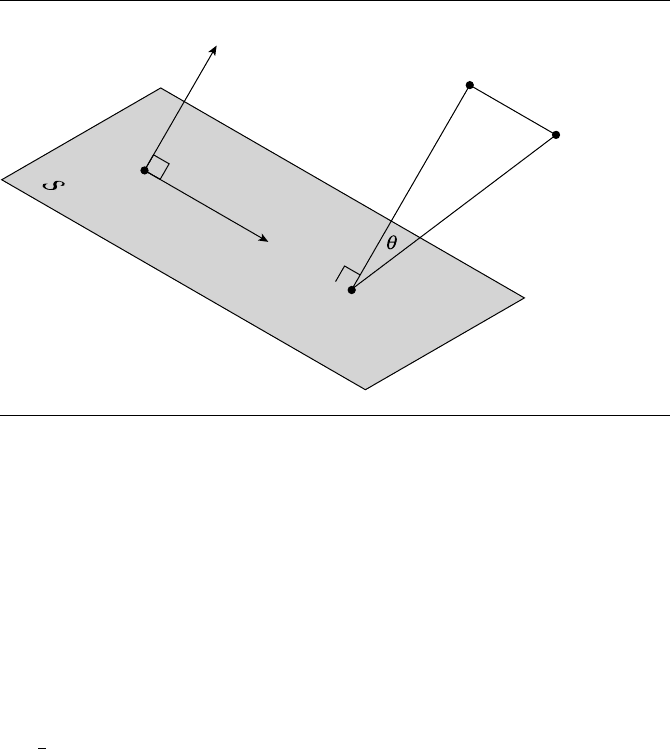
General Shearing

A more general shear is deﬁned by a shearing plane S, unit vector ˆv in S, and

shear angle θ . The plane S is deﬁned by a point Q on the plane and a normal ˆn.

The shear transform moves a family of parallel planes in space so that the planes

remain parallel; one plane (the one deﬁning it) is unmoved. Goldman (1991) gives

the construction of a shearing transform matrix (see Figure 4.25): for any point P ,let



be its orthogonal projection on S; then, construct point P



=P + t ˆv with t such

that







P =θ. If we apply a shear transform to P ,wegetP



. The transformation

Q,ˆn,v,θ



I +tan θ(ˆn ⊗ˆv)



−(Q ·ˆn) ˆv 1



Goldman notes that the determinant of this matrix is 1, and thus the shear transfor-

mation preserves volumes (note that −π/2 <θ<π/2).

The general 3D shear matrix can be constructed along different lines, and perhaps

more simply. The vectors ˆv and ˆn, along with the point Q, deﬁne an afﬁne frame (the

third basis vector is ˆv ×ˆn). If we have a point P =Q +y

ˆn +y

ˆv + y

( ˆn ×ˆv), then

the shearing operation would map that point to

158 Chapter 4 Matrices, Vector Algebra, and Transformations

T(P)= T (Q) + y

T(ˆn) + y

T(ˆv) + y

T(ˆn ×ˆv)

= Q + y

( ˆn + tan θ ˆv) + y

ˆv + y

( ˆn ×ˆv)

= Q + y

ˆn + (y

+ y

tan θ)ˆv + y

( ˆn ×ˆv)

The matrix relative to the afﬁne frame is







1 tan θ 00

0100

0010







whose upper-left 3 ×3blockH the reader should recognize as the 2D y-shear matrix

yx,θ

from the previous section (the basis vector v is acting as the y-axis for that

frame).

In terms of the standard Euclidean basis, if we have a rotation matrix

R =





ˆn

ˆv

ˆn ×ˆv





and

y =

[

]

then

P = Q +yR

and

T(P)= Q +yHR

= Q + (P − Q)R

The matrix T for T is

ˆn,ˆv,Q,θ





Q(I

− R

HR) 1



4.8 Projections

Projections are a class of transformations that all share the characteristic that they

transform points from an n-dimensional frame (coordinate system) to a frame with

4.8 Projections 159

less than n dimensions (generally, n − 1). The most signiﬁcant use of projection

in computer graphics is in the rendering pipeline of graphics display systems and

libraries, where three-dimensional objects are projected onto a plane before being

rasterized and displayed on a terminal screen.

The class of projective transformations contains two subclasses that are of par-

ticular interest in computer graphics: parallel and perspective. A projection can be

deﬁned as the result of taking the intersection of a line connected to each point on a

geometric object with a plane. In parallel projection, all of these projectors are paral-

lel, while in perspective projection, the projectors meet at a common point, referred

to as the center of projection. As pointed out in Foley et al. (1996, Section 6.1), you

can justiﬁably consider the center of projection in a parallel projection to be a point

at inﬁnity.

In the following sections, we’ll show how orthographic and perspective projection

transformation matrices can be constructed using only vector algebra techniques.

For a thorough treatment of the various subclasses of parallel projections, and the

construction of parallel and perspective projection transformation matrices for the

purposes of creating viewing transformations, see Foley et al. (1996, Chapter 6).

4.8.1 Orthographic

Orthographic projection (also called orthogonal) is the simplest type of projection

we’ll discuss: it consists of merely projecting points and vectors in a perpendicular

fashion onto a plane, as shown in Figure 4.26. As in the case of the mirror transform,

we deﬁne the plane M byapointQ on the plane and (unit) normal vector ˆu.

Orthographic projection of a vector v is simply the usual sort of projection we’ve

been using all along: we project v onto ˆu to get the parallel and perpendicular com-

ponents, and note that since v

⊥

is position independent, the relative location of Q is

not considered. Thus, we have

T(v) =v

⊥

=v −(v ·ˆu) ˆu

(4.33)

The transformation of a point P is similarly trivial:

T(P)= Q + T(v)

= Q + T(P − Q)

= P −((P − Q) ·ˆu) ˆu

(4.34)

The matrix representation of this is accomplished by factoring out v from Equa-

tion 4.33 to give the upper left-hand n × n submatrix:

ˆu

I −( ˆu ⊗ˆu)

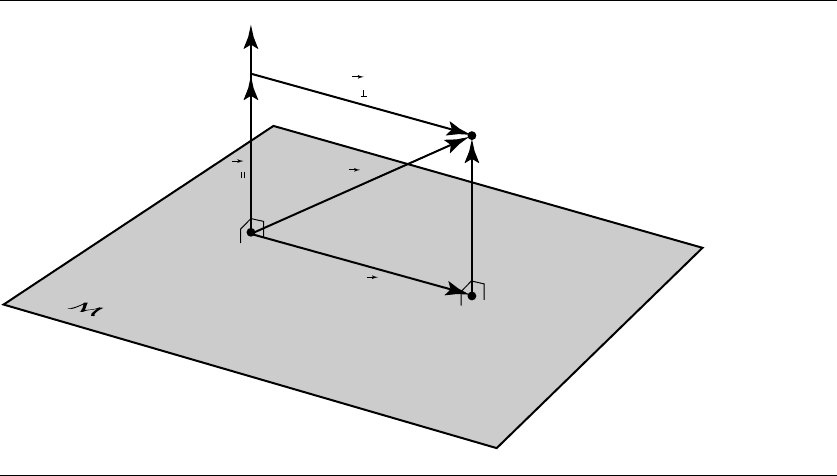
160 Chapter 4 Matrices, Vector Algebra, and Transformations

T(P)

T(v)

Figure 4.26 Orthographic (orthogonal) projection.

The bottom row is computed as usual by factoring out the above and the point P

from Equation 4.34:

ˆu,Q



ˆu



(Q ·ˆu) ˆu 1



4.8.2 Oblique

Oblique (or parallel) projection is simply a generalization of orthographic

projection—the projection is parallel, but the plane need not be perpendicular to

the projection “rays.” Again, the projection plane M is deﬁned by a point Q on it

and a normal vector ˆu, but since ˆu no longer also deﬁnes the direction of projection,

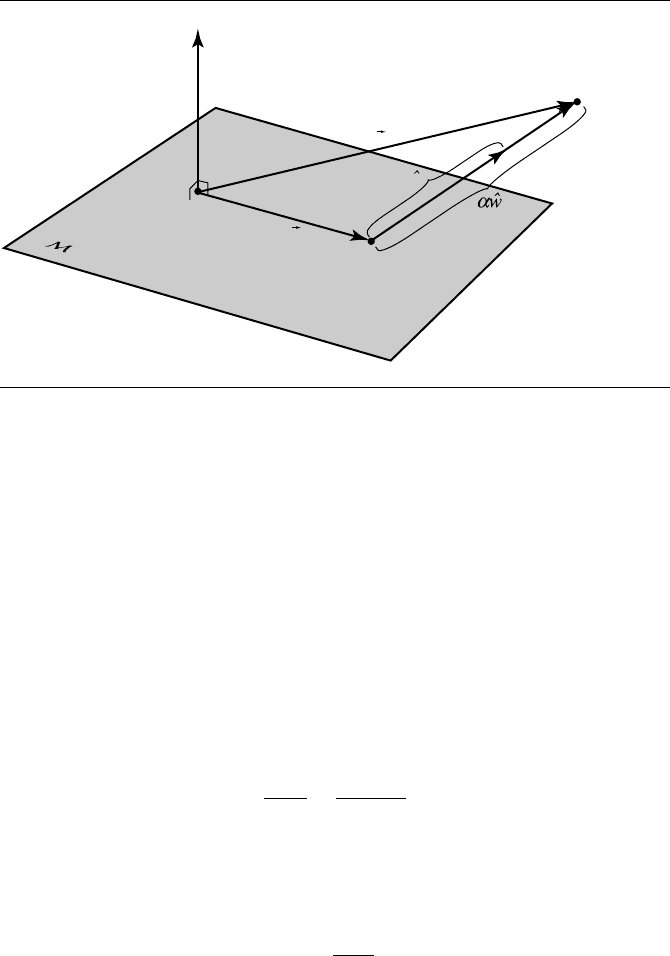
we need to specify another (unit) vector ˆw as the projection direction, as shown in

Figure 4.27.

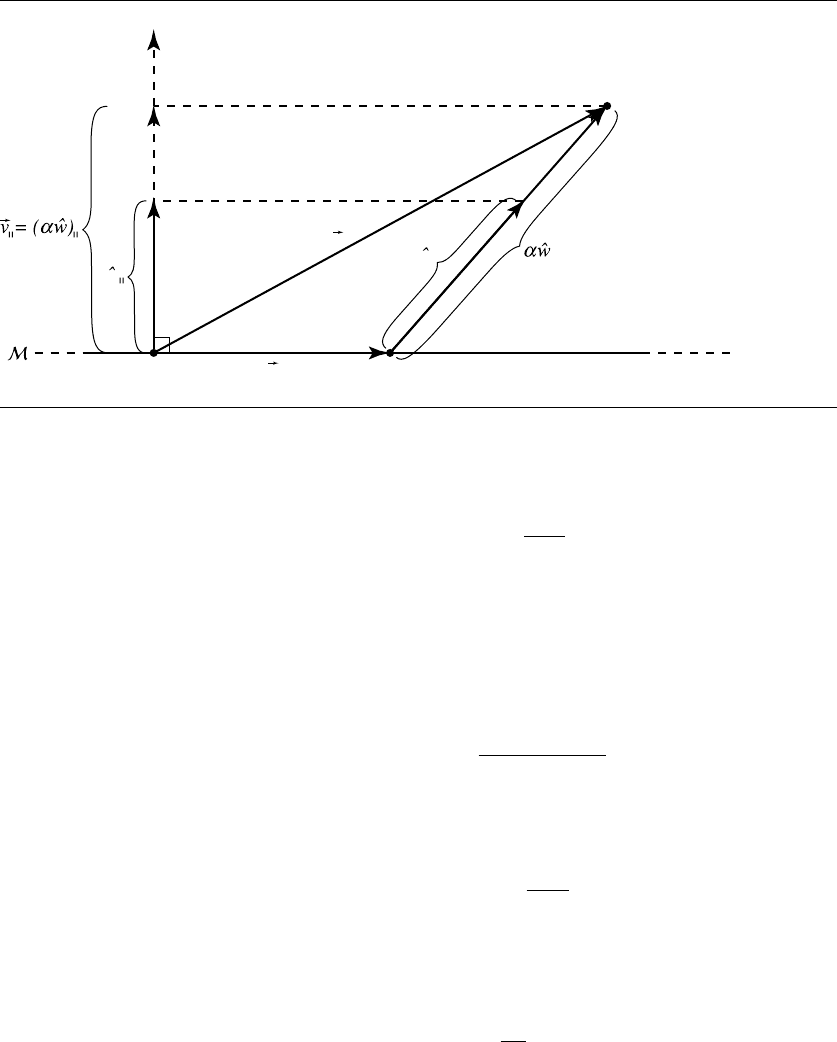
An edge-on diagram of this (Figure 4.28) will help us explain how to determine

the transformation of vectors. We can start out by observing that

v = T(v) + α ˆw

4.8 Projections 161

T(P)

T(v)

Figure 4.27

Oblique projection.

which we can rearrange as

T(v) =v −α ˆw (4.35)

Obviously, what we need to compute is α, but this is relatively straightforward, if

we realize that

v



=(α ˆw)



We can exploit this as follows:

v



ˆw



(α ˆw)



ˆw



= α

which we can rewrite using the deﬁnition of the dot product:

α =

v ·ˆu

ˆw ·ˆu

(4.36)

We then can substitute Equation 4.36 into Equation 4.35 to get the transformation

for vectors:

162 Chapter 4 Matrices, Vector Algebra, and Transformations

T(P)

T(v )

Figure 4.28 Edge-on view of oblique projection.

T(v) =v −

v ·ˆu

ˆw ·ˆu

ˆw (4.37)

We can then, as usual, employ the deﬁnition of point and vector addition and sub-

traction to obtain the formula for transforming a point:

P = Q + T(v)

= Q + T(P − Q)

= P −

((P − Q) ·ˆu) ˆw

ˆw ·ˆu

(4.38)

To convert this to matrix representation, we apply the usual technique of extract-

ing v from Equation 4.37 to compute the upper left-hand n × n submatrix:

ˆu, ˆw

I −

( ˆu⊗ˆw)

ˆw·ˆu

To compute the bottom row of the transformation matrix, we extract that and the P

from Equation 4.38, and the complete matrix looks like this:

ˆu,Q, ˆw



ˆu, ˆw



Q·ˆu

ˆw·ˆu

ˆw 1



4.8 Projections 163

T(P)

T(P

)

T(P

)

Figure 4.29 Perspective projection.

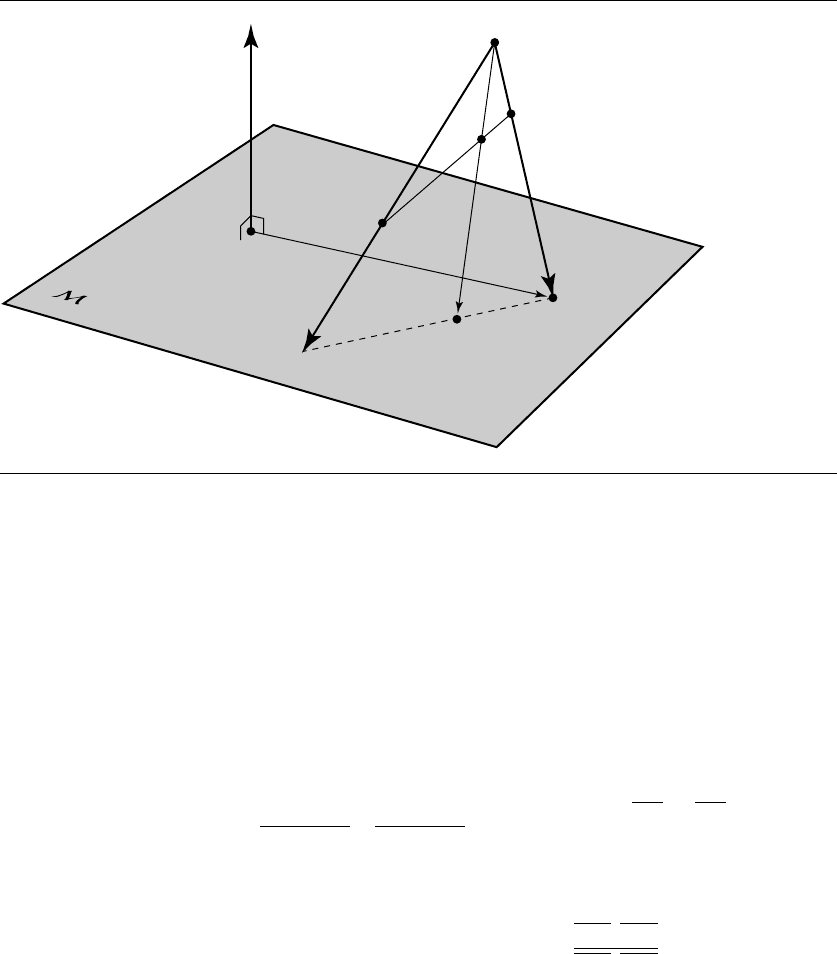
4.8.3 Perspective

Perspective projection is not an afﬁne transformation; it does not map parallel lines

to parallel lines, for instance. Unlike the orthographic and parallel projections, the

projection vectors are not uniform for all points and vectors; rather, there is a pro-

jection point or perspective point, and the line of projection is deﬁned by the vector

between each point and the perspective point, as shown in Figure 4.29.

Perspective projection does, however, preserve something called cross-ratios.Re-

call that afﬁne maps preserve ratios: given three collinear points P , R, and Q, the

ratio of the distance between P and R (which we notate as

PR)to

RQ is the same as

the ratio of

T(P)T(R)to T(R)T(Q)(see Figure 3.36).

The cross-ratio is deﬁned as follows: given four collinear points P , R

, R

, and Q,

the cross-ratio is

CrossRatio(P , R

, R

, Q) =

as shown on the left side of Figure 4.30. Preservation of cross-ratio means that the

following holds: