Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

164 Chapter 4 Matrices, Vector Algebra, and Transformations
P
Q
T(P)
T(PR
1
)
T(Q)
R
1
R
2
T(R
1
)
T(R
2
)
T(R
1
Q)
T(PR
2
)
T(R
2
Q)
PR
1
PR
2
R
2
Q
R
1
Q
T
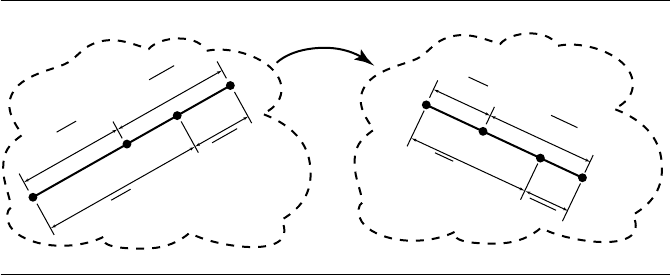
Figure 4.30 Cross-ratio.
CrossRatio(P , R
1
, R
2
, Q) = CrossRatio(T (P ), T(R
1
), T(R
2
), T (Q))
as shown in Figure 4.30. A more thorough treatment of the cross-ratio can be found
in Farin (1990) or DeRose (1992).
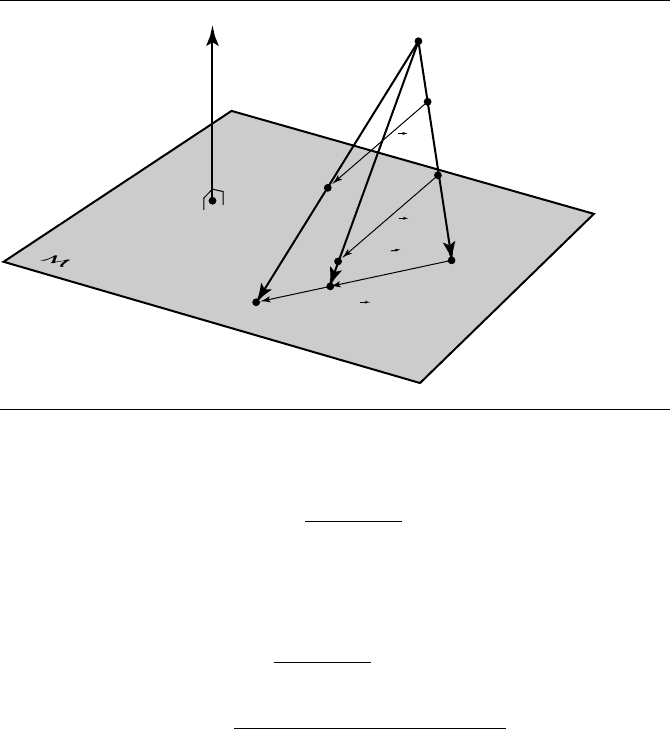
It is important to understand that perspective projection of vectors is ill defined.
If we take any two sets of points whose difference is a given vector, the vector between
the parallel projections of each set of points will be the same. This is not true with
the perspective projection; consider Figure 4.31, where we have two such pairs of
points, (P
1
, P
2
) and (P
3
, P
4
), each of which differ by the vector v
1
=v
2
.However,
if we look at the vectors between the projections of these pairs of points (T(v
1
) =
T(P
2
) −T(P
1
) and T(v
2
) =T(P
4
) −T(P
3
), respectively), it’s clear that these vectors
are not equivalent.
However, perspective projection is well defined for points. Clearly, T(P)is a point
at the end of a scaled version of the vector between P and S:
T(P)= P +α(S − P) (4.39)
Another way of looking at this is to note that
T(P)− Q = (P − Q) + α(S − P)
which must also be perpendicular to the plane normal, so we have
0 =ˆu ·
(
(P − Q) + α(S − P)
)
=ˆu · (P −Q) + α ˆu · (S − P)
If we solve the above for α,weget
4.9 Transforming Normal Vectors 165
Q
P
1
T(P
1
)
P
2
T(P
2
)
P
3
P
4
S
v
1
v
2
T(v
2
)
T(v
1
)
û
Figure 4.31 Perspective map for vectors.
α =
ˆu · (Q − P)
ˆu · (S − P)
(4.40)
We can now substitute Equation 4.40 into Equation 4.39 and do a little vector arith-
metic to yield the final formula:
T(P)= P +
(Q − P)·ˆu
(S −P)·ˆu
(S −P)
=
((S −Q) ·ˆu)P + ((Q − P)·ˆu)S
(S −P)·ˆu
The transformation matrix for this, then, is
T
u,Q,S
=
((S −Q) ·ˆu)I −ˆu ⊗ S −ˆu
T
(Q ·ˆu)S S ·ˆu
4.9 Transforming Normal Vectors
Vectors, as we saw, can be transformed by matrix multiplication in the same way
as points. A natural-seeming application of this principle would be to treat surface
normal vectors in this way, but it turns out this is (in general) incorrect. As this may
166 Chapter 4 Matrices, Vector Algebra, and Transformations
x
z
x
n
n
yy
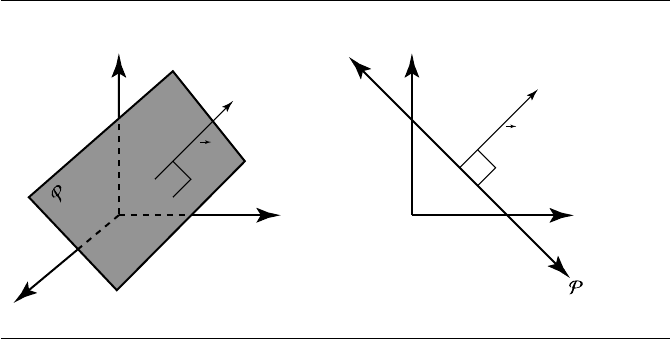
Figure 4.32 The plane x +y =k.
seem initially counterintuitive, a bit of explanation as to why this is wrong may be
useful, before we explain the correct method.
The culprit here is nonuniform scaling. An example by Eric Haines (1987) shows
this quite nicely: Consider a plane in three-dimensional space. If we look down the z-
axis, this would appear as a line with a 45
◦
angle, as shown in Figure 4.32. The normal
to this plane is n = [
110
]. Suppose we have a nonuniform scale transform T
where only x is scaled by a factor of two. This gives us a transformation matrix
T =
2000
0100
0010
0001
If we apply this transformation to the plane and the normal, we get the plane
stretched as expected. However, consider the transformation on the normal
T(n) =nT =
[
110
]
2000
0100
0010
0001
=
[
210
]
as shown in Figure 4.33. Clearly, this is incorrect. What’s going on? The problem is
that a normal vector isn’t really a vector in the usual sense. Rather, a normal to a
surface is actually the cross product of two (linearly independent) vectors that are
tangent to the surface
n =u ×v
4.9 Transforming Normal Vectors 167
x
y
n
T(x)
y
T(n)
T
T( )
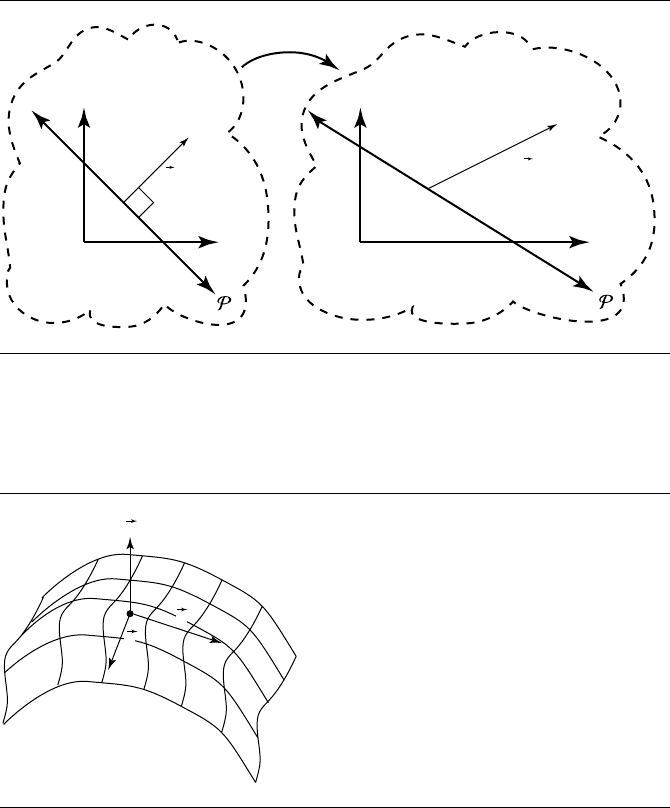
Figure 4.33 Incorrectly transformed normal.
n
u
v
Figure 4.34 Normal as cross product of surface tangents.
as shown in Figure 4.34. If T is a linear transform of the space containing the surface,
then the transformed tangents are T(u) and T(v), both tangent to the transformed
surface. A normal to the transformed surface can be chosen as m = T(u) × T(v).
But m (as we have seen) is not necessarily the transformed normal T(n); T(u ×v) =
T(u) ×T(v), and more generally T(u ×v) is not necessarily parallel to T(u) ×T(v).
168 Chapter 4 Matrices, Vector Algebra, and Transformations
Perpendicularity of n with respect to any tangent vector u can be expressed as
u ·n =un
T
= 0
We want the transformed normal to be perpendicular to the transformed tangent(s):
T(u) ·m = 0
If we just crunch through the math, we get
0 =un
T
=uTT
−1
n
T
= (uT)(n(T
−1
)
T
)
T
= T(u) · (n(T
−1
)
T
)
Therefore, a normal vector to the transformed surface is m =n(T
−1
)
T
,wheren is a
normal vector to the surface. The matrix (T
−1
)
T
is called the inverse transpose of T.
You should be aware that even if n is unit length, the vector m =n(T
−1
)
T
is not
necessarily unit length, so for applications requiring unit-length normals, m needs
to be normalized.
Recommended Reading
A thorough and deep understanding of vector algebra is a powerful tool for the
computer graphics programmer. Unfortunately, good coverage is rare in the more
widely read graphics literature, and courses covering it are rare in computer science
programs. Programmers with an academic background in mechanical engineering
or physics are more likely to have been exposed to this type of material, although
it is probably possible to get through some undergraduate mathematics programs
without an explicit course in vector analysis. This may be more the case now than
in the past, considering the very large number of textbooks with “Vector Analysis” in
their title (or as their title) that are notated as “out of print” in book search databases.
Goldman (1987) cites the following two books:
E.B. Wilson, Vector Analysis, Yale University Press, New Haven, CT, 1958.
A. P. Wills, Vector Analysis with an Introduction to Tensor Analysis, Dover Publica-
tions, New York, 1958.
Recommended Reading 169
Several other useful mathematically oriented sources are
Murray Spiegel, Schaum’s Outline of Theory and Problems of Vector Analysis, and
an Introduction to Tensor Analysis, McGraw-Hill, New York, 1959.
Banesh Hoffman, About Vectors, Dover, Mineola, NY, 1966, 1975.
Harry Davis and Arthur Snider, Introduction to Vector Analysis, McGraw-Hill,
New York, 1995.
More related to computer graphics are
Ronald Goldman, “Vector Geometry: A Coordinate-Free Approach,” in 1987
SIGGRAPH Course Notes 19: Geometry for Computer Graphics and Computer
Aided Design, ACM, New York, 1987.
Ronald Goldman, “Illicit Expressions in Vector Algebra,” in ACM Transactions on
Graphics, Vol. 4, No. 3, July 1985.
Tony D. DeRose, “A Coordinate-Free Approach to Geometric Programming,”
Math for SIGGRAPH: Course Notes 23, SIGGRAPH ’89, pages 55–115, July 1989.
Tony D. DeRose, Three-Dimensional Computer Graphics: A Coordinate-Free
Approach. Unpublished manuscript, University of Washington, 1992 (www.cs
.washington.edu).
James R. Miller, “Vector Geometry for Computer Graphics,” IEEE Computer
Graphics and Applications, Vol. 19, No. 3, May 1999.
James R. Miller, “Applications of Vector Geometry for Robustness and Speed,”
IEEE Computer Graphics and Applications, Vol. 19, No. 4, July 1999.
Chapter
5Geometric
Primitives in 2D
This chapter contains the definitions for various two-dimensional geometric primi-
tives that are commonly used in applications. Some of the primitives have multiple
representations. A geometric query involving an object might be more effectively for-
mulated with one representation than another. The discussion about a query will
indicate which representation is more appropriate.
In geometric queries with objects such as polygons, the object can be treated
as a one-dimensional or a two-dimensional object. For example, the triangle as a
one-dimensional object is just the closed polyline perimeter. As a two-dimensional
object, the triangle refers to its polyline perimeter and the region that it bounds. Some
objects have distinct names for the two possibilities. For example, circle refers to the
one-dimensional curve, and disk refers to the curve and the region it bounds. When
necessary, the distinction will be made clear. In the absence of distinct names, the
word solid will be used. For example, the method for computing distance between
a point and a triangle treats the triangle as a solid. If a point is inside the triangle
boundary, then the distance is zero.
5.1 Linear Components
Linear components may be represented either implicitly or parametrically. In the case
of lines, both representations have equal expressive power, but as we shall see, the
parametric form is convenient for representing rays and segments.
171
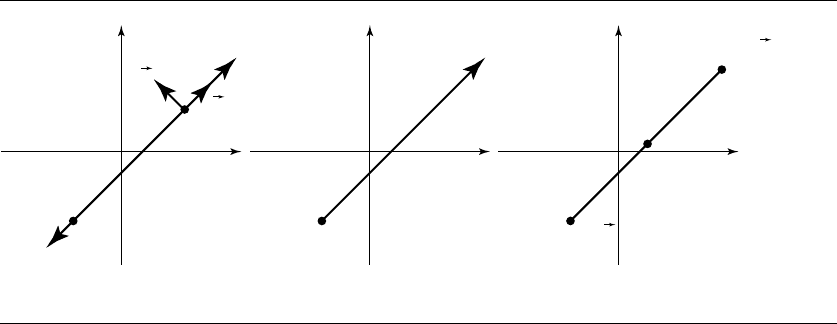
172 Chapter 5 Geometric Primitives in 2D
Positive
side
n
d
Negative
side
(a) (b) (c)
PP
P
0
= C – rd
P
1
= C + rd
C
Figure 5.1 Examples of (a) a line, (b) a ray, and (c) a segment.
5.1.1 Implicit Form
A line is defined by n · X = d. A normal vector to the line is n = (n
0
, n
1
), and points
on the line are represented by the variable X = (x
0
, x
1
).IfP is a specific point on the
line, then the equation for the line is n · (X −P)= 0 =n · X −d,wheren · P = d.
This definition for a line is called the normal form. A direction vector for the line is
d =(d
0
, d
1
) = (n
1
, −n
0
). Figure 5.1(a) illustrates a typical line in the plane. Of course
we cannot draw a line having infinite extent in both directions. The arrowheads are
meant to imply that what is drawn in fact does extend infinitely in both directions. A
line partitions the plane into two half-planes. The half-plane on the side of the line
to which the normal points is called the positive side of the line and is represented
algebraically by n · X − d>0. The other half-plane is called the negative side of the
line and is represented algebraically by n · X −d<0.
Although n is not required to be a unit-length vector, it is convenient in many
geometric queries if it is unit length. In this case
ˆ
d is also unit length. The point P
and the unit-length vectors
ˆ
d and ˆn form a right-handed coordinate system where P
is the origin and the unit-length vectors are the directions of the coordinate axes. See
Section 3.3.3 for a discussion of coordinate systems. Any point X can be represented
by X = P +y
0
ˆ
d + y
1
ˆn,wherey
0
=
ˆ
d · (X −P) and y
1
=ˆn · (X −P). The positive
side of the line is characterized by y
1
> 0, the negative side of the line is characterized
by y
1
< 0, and y
1
= 0 represents the line itself.
Another commonly seen representation of a line is the implicit form
ax + by + c = 0
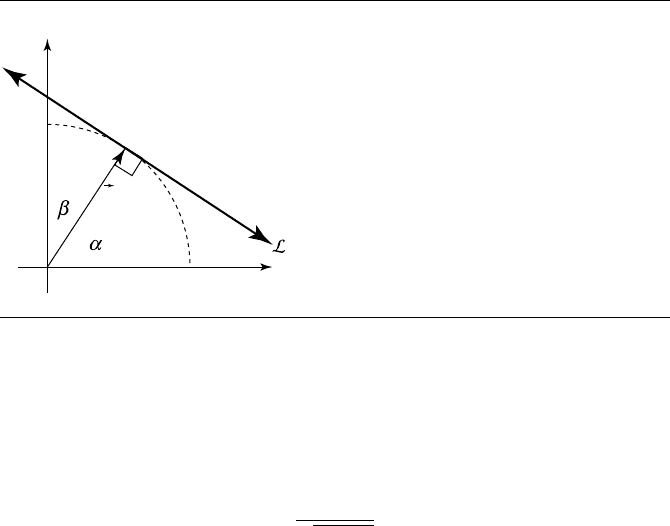
5.1 Linear Components 173
x
y
r
Figure 5.2
Implicit definition of a line.
This can be seen to be equivalent to the previous definition if we let ˆn =[
ab
], X =
[
xy
], and d =−c.Ifa
2
+ b
2
= 1, then the line equation is said to be normalized;
a nonnormalized equation can be normalized by multiplying through by
1
√
a
2
+ b
2
This, of course, is equivalent in the other representation as ˆn=1. With the equa-
tion so normalized, we can more easily gain an intuition of the coefficients:
a =cos α
b = cos β
c =r
In other words, a and b are the x- and y-components of a vector perpendicular to the
line (that is, ˆn), and c is the minimum (signed) distance from the line to the origin,
as can be seen in Figure 5.2.
5.1.2 Parametric Form
The parametric form of the line is X(t) = P + t
d for t ∈ R .Aray is a line with the
parametric restriction t ≥ 0. The origin of the ray is P . Figure 5.1(b) illustrates a ray
in the plane. As with drawing a line, it is not possible to draw a ray with infinite
extent, so we use an arrowhead to imply that the ray continues infinitely in the
specified direction. A line segment, or simply segment, is a line with the parametric
restriction t ∈ [t
0
, t
1
]. If P
0
and P
1
are end points of the segment, the standard form
