Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

184 Chapter 5 Geometric Primitives in 2D
d
0
≠ 0, d
1
= 0, e
1
= 0, d
0
r < 0
No solution
d
0
≠ 0, d
1
= 0, e
1
= 0, d
0
r > 0
Cylinder
d
0
≠ 0, d
1
= 0, e
1
≠ 0
Parabola
d
0
≠ 0, d
1
= 0, e
1
= 0, r = 0
Line
Figure 5.14 Solutions to the quadratic equation depending on the values for d
0
= 0, d
1
= 0, e
1
,
and r.
C
X – C
2
= r
X(t) = C + r[cos t sin t]
t
rCr
Figure 5.15 Circles defined in distance (implicit) and parametric forms.
the factored form states that D
1/2
R(X −C)=1. The vector whose length is indi-
cated here must be unit length, so D
1/2
R(X − C) =ˆu(t) is a valid choice. Solving
for X produces the parametric form. The quadratic form is X
T
AX + B · X +c = 0,
where A isa2×2 matrix whose diagonal entries are positive and whose determinant
is positive. Moreover, C =−A
−1
B/2 and R
T
DR = A/(B
T
A
−1
B/4 − c).
The area of an ellipse is π+
0
+
1
for the factored and parametric forms and
π(B
T
A
−1
B/4 − c)/
√
det(A) for the quadratic form.

5.6 Polynomial Curves 185
C
l
0
l
1
Figure 5.16 Definition of an ellipse.
5.6 Polynomial Curves
A polynomial curve in the plane is a vector-valued function X : D ⊂ R →R ⊂ R
2
,
say, X(t), and has domain D and range R. The components X
i
(t) of X(t) areeacha
polynomial in the specified parameter
X
i
(t) =
n
i
j=0
a
ij
t
j
where n
i
is the degree of the polynomial. In most applications the degrees of the
components are the same, in which case the curve is written as X(t) =
n
j=0
A
j
t
j
for known points A
j
∈R
2
. Even if the degrees are different, we can still use the vector
notation by selecting n =max
i
n
i
and setting coefficients a
ij
=0 for n
i
<j≤ n.The
domain D in the applications is typically either R or [0, 1]. A rational polynomial curve
is a vector-valued function X(t) whose components X
i
(t) are ratios of polynomials
X
i
(t) =
n
i
j=0
a
ij
t
j
m
i
j=0
b
ij
t
j
where n
i
and m
i
are the degrees of the numerator and denominator polynomials.
A few common types of curves that occur in computer graphics are B
´
ezier curves,
B-spline curves, and nonuniform rational B-spline (NURBS) curves. Only the defi-
nitions for these curves are given here. Various properties of interest may be found in
other texts on curves and surfaces (Bartels, Beatty, and Barsky 1987; Cohen, Riesen-
feld, and Elber 2001; Farin 1990, 1995; Rogers 2001; Yamaguchi 1988).
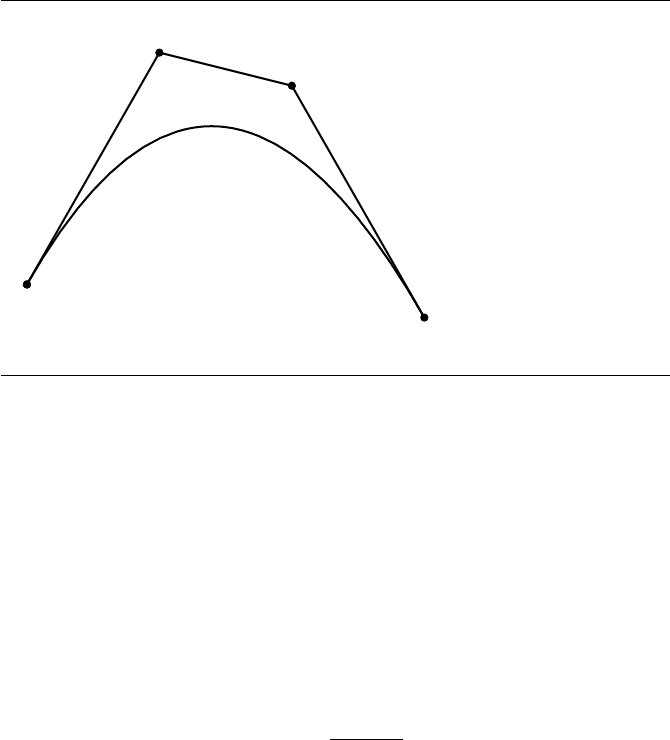
186 Chapter 5 Geometric Primitives in 2D
P
0
P
1
P
3
P
2
Figure 5.17 A cubic B
´
ezier curve.
5.6.1 B
´
ezier Curves
A planar B´ezier curve is constructed from a set of points P
i
∈R
2
for 0 ≤i ≤ n, called
control points,by
X(t) =
n
i=0
n
i
t
i
(1 − t)
n−i
P
i
=
n
i=0
B
i
(t)P
i
, t ∈ [0, 1]
where
n
i
=
n!
i!(n − i)!
is the number of combinations of i items chosen from a set of n items. The real-
valued polynomials B
i
(t) are called the Bernstein polynomials, each of degree n.The
polynomial components of X(t) are therefore also of degree n. Figure 5.17 shows a
cubic B
´
ezier curve, along with the control points and control polygon.
5.6.2 B-Spline Curves
A planar B-spline curve of degree j is constructed from a set of points P
i
∈ R
2
, called
control points, and a monotone set of parameters t
i
(i.e., t
i
≤ t
i+1
), called knots, for
0 ≤i ≤ n,by
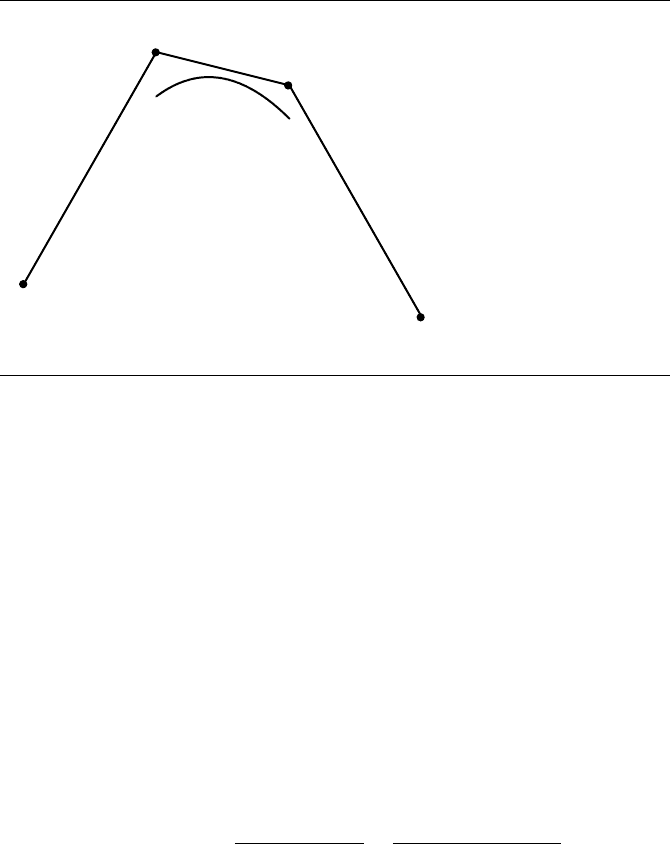
5.6 Polynomial Curves 187
P
0
P
1
P
3
P
2
Figure 5.18 A cubic B-spline curve.
X(t) =
n
i=0
B
i,j
(t)P
i
where t ∈[t
0
, t
n
]and 1 ≤j ≤n.Thevector(t
0
, ..., t
n
) is called a knot vector. The real-
valued polynomials B
i,j
(t) areofdegreej and defined by the Cox–de Boor recursion
formulas
B
i,0
(t) =
1, t
i
≤ t<t
i+1
0, otherwise
and
B
i,j
(t) =
(t − t
i
)B
i,j −1
(t)
t
i+j −1
− t
i
+
(t
i+j
− t)B
i+1,j −1
(t)
t
i+j
− t
i+1
for 1 ≤ j ≤ n. The polynomial components of X(t) are actually defined piecewise
on the intervals [t
i
, t
i+1
]. On each interval the polynomial is of degree j. The knot
values are not required to be evenly spaced. In this case the curve is said to be a
nonuniform B-spline curve. If the knot values are equally spaced, then the curve is
called a uniform B-spline curve. Figure 5.18 shows a uniform cubic B-spline curve,
along with the control points and control polygon.

188 Chapter 5 Geometric Primitives in 2D
5.6.3 NURBS Curves
A planar nonuniform rational B-spline curve or NURBS curve is obtained from a
nonuniform B-spline polynomial curve in three dimensions. The control points are
(P
i
,1) ∈ R
3
for 0 ≤ i ≤ n, with weights w
i
> 0, and the polynomial curve is
(Y (t ), w(t)) =
n
i=0
B
i,j
(t)w
i
(P
i
,1)
where B
i,j
(t) is the same polynomial defined in the previous subsection. The NURBS
curve is obtained by treating (Y (t), w(t)) as a homogeneous vector and dividing
through by the last component (often referred to as the weight) to obtain a projection
in three dimensions
X(t) =
Y(t)
w(t)
=
n
i=0
R
i,j
(t)P
i
where
R
i,j
(t) =
w
i
B
i,j
(t)
n
k=0
w
k
B
k,j
(t)
Chapter
6Distance in 2D
This chapter contains information on computing distance between geometric prim-
itives in 2D. An application might not want to pay the price for an expensive square
root calculation, so many of the algorithms in this chapter provide a construction for
squared distance. Of course, fundamental to any distance algorithm is the squared
distance between two points X =(x
0
, x
1
) and Y = (y
0
, y
1
)
Distance
2
(X, Y)=X − Y
2
= (x
0
− x
1
)
2
+ (y
0
− y
1
)
2
(6.1)
We will discuss algorithms for computing the distance between a point and an-
other object first; other combinations are discussed later in the chapter. When both
objects are convex with polyline or polygonal boundaries, including the degenerate
case when one is a linear component, the distance algorithms can be implemented
by applying a derivativeless numerical minimizer using the point-object formulas.
For example, the distance between a line segment and a triangle can be computed
as a minimization of a one-dimensional function. If F(X, T)is the squared distance
between the point X and the triangle T , then the squared distance between a line
segment X(t) = P
0
+ t(P
1
− P
0
), t ∈ [0, 1], and the triangle is G(t) = F(X(t), T).
A numerical minimizer can be applied to G(t) for t ∈ [0, 1]. Such an iterative ap-
proach certainly can produce a reasonable numerical estimate for the squared dis-
tance, but typically the approach takes more time to find the estimate than a method
that computes the squared distance using a noniterative method. The trade-off is ease
of implementation versus time efficiency of the algorithm.
189
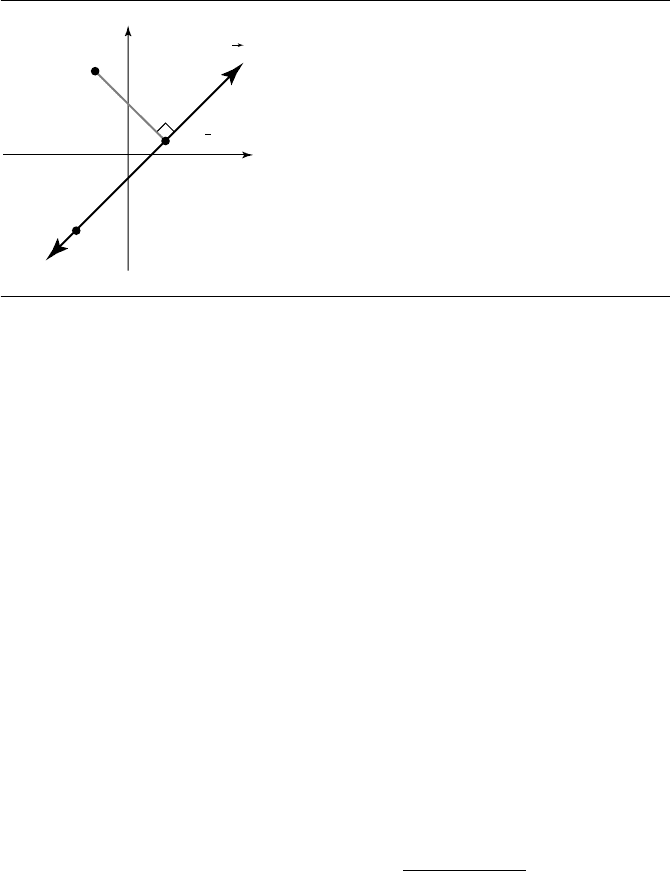
190 Chapter 6 Distance in 2D
P
d
Y
X(t)
Figure 6.1 Closest point X(
¯
t) on a line to a specified point Y .
6.1 Point to Linear Component
This section covers the distance algorithms for the three combinations of points with
lines, rays, or line segments: point-line, point-ray, and point-segment.
6.1.1 Point to Line
Given a point Y and a line L parameterized as X(t) = P + t
d, the closest point on
the line to Y is the projection X(
¯
t) of Y onto the line for some parameter value
¯
t.
Figure 6.1 illustrates the relationship. As shown in the figure, the vector Y − X(
¯
t)
must be perpendicular to the line direction
d. Thus,
0 =
d · (Y − X(
¯
t)) =
d · (Y − P −
¯
t
d) =
d · (Y − P)−
¯
t
d
2
and the parameter of the projection is
¯
t =
d ·(Y −P)/
d
2
. The squared distance is
Y − P −
¯
t
d
2
. Some algebra leads to
Distance
2
(Y , L) =Y −P
2
−
d · (Y − P)
2
d
2
(6.2)
If
d is already unit length, then the equation is slightly simplified in that
ˆ
d=1 and
no division is required to compute the squared distance.
If the line is represented as n · X =c, the closest point K on the line satisfies the
relationship Y = K + s n for some s. Dotting with n yields n · Y =n · K + sn
2
=
c + sn
2
,sos = (n · Y − c)/n
2
. The distance between the point and the line is
Y − K=|s|n,or

6.1 Point to Linear Component 191
Distance
Y , L
=
|n · Y − c|
n
(6.3)
If n is unit length, then the equation is slightly simplified in that ˆn=1 and no
division is required to compute the distance.
Equation 6.3 looks a lot simpler than Equation 6.2 and is less expensive to com-
pute. The relationship between the two equations is clear from the following identity
with the assumption that
ˆ
d and ˆn are unit length:
Y − P
2
= (Y − P)
T
(Y − P)
= (Y − P)
T
I(Y − P)
= (Y − P)
T
(
ˆ
d
ˆ
d
T
+ˆn ˆn
T
)(Y − P)
=
ˆ
d · (Y − P)
2
+
ˆn · (Y −P)
2
=
ˆ
d · (Y − P)
2
+
ˆn · Y −c
2
The key identity in the construction is I =
ˆ
d
ˆ
d
T
+ˆn ˆn
T
,whereI is the 2 × 2 identity
matrix. This identity is true for any pair of orthonormal vectors. The proof relies on
the fact that {
ˆ
d, ˆn} is an orthonormal basis for R
2
, so every vector can be represented
as
IX = X =(
ˆ
d
T
X)
ˆ
d + ( ˆn
T
X)ˆn = (
ˆ
d
ˆ
d
T
)X + ( ˆn ˆn
T
)X = (
ˆ
d
ˆ
d
T
+ˆn ˆn
T
)X
Since this is true for all X, it must be that I =
ˆ
d
ˆ
d
T
+ˆn ˆn
T
. Observe that the term
ˆ
d
ˆ
d
T
is not to be confused with the dot product
ˆ
d
T
ˆ
d.Thevector
ˆ
d isa2×1vector,so
ˆ
d
T
isa1×2 vector and the product
ˆ
d
ˆ
d
T
isa2× 2 matrix.
6.1.2 Point to Ray
The construction is similar to that of point to line. The difference is that in some cases
the projection of Y onto the line containing the ray R might not be a point on the
ray. In a sense, Y is behind the ray. Figure 6.2 shows the two possibilities. Figure 6.2(a)
shows the case when the projection is onto the ray. In this case
¯
t ≥ 0, and Equations
6.2 and 6.3 apply. Figure 6.2(b) shows the case when the projection is not onto the
ray. In this case
¯
t<0, and the closest point to Y is the ray origin P . The squared
distance is
Distance
2
Y , R
=
Y − P
2
−
d·(Y −P)
2
d
2
,
d · (Y − P)>0
Y − P
2
,
d · (Y − P)≤ 0
(6.4)
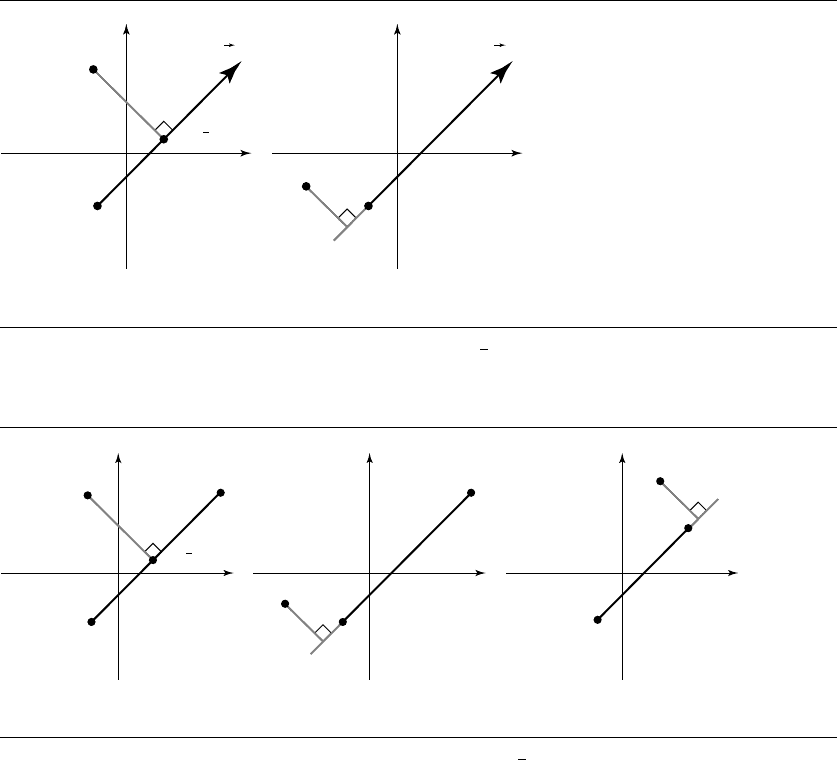
192 Chapter 6 Distance in 2D
P
Y
X(t)
(a)
P
Y
(b)
d d
Figure 6.2 Closest point on a ray to a given point: (a) X(t) closest to Y ; (b) P closest to Y .
P
0
P
1
Y
P
1
X(t)
(a)
P
0
P
0
P
1
Y
(b)
Y
(c)
Figure 6.3 Closest point on a segment to a given point: (a) X(t) closest to Y ; (b) P
0
closest to Y ; (c) P
1
closest to Y .
6.1.3 Point to Segment
The construction is also similar to that of point to line. The difference now is that
the projection of Y onto the line might not lie on the line segment S. The projection
could lie behind the initial point or ahead of the final point of the segment. Figure 6.3
shows the three possibilities. The direction vector is
d =P
1
−P
0
, the difference of end
points for the line segment. The parameter interval is [0, 1]. The value
¯
t is computed,
just as for the line, but then it is tested against the parameter interval [0, 1] for the
6.1 Point to Linear Component 193
segment. The squared distance is
Distance
2
Y , S
=
Y − P
0
2
,
¯
t ≤ 0
Y − (P
0
+
¯
t
d)
2
,
¯
t ∈ (0, 1)
Y − P
1
2
,
¯
t ≥ 1
(6.5)
where
¯
t =
d ·(Y −P
0
)/
d
2
. For the symmetric form (see Section 5.1.2), the squared
distance is
Distance
2
(Y , S) =
Y − (C − r
d)
2
,
¯
t ≤−r
Y − (C +
¯
t
d)
2
, |
¯
t| <r
Y − (C + r
d)
2
,
¯
t ≥ r
(6.6)
where
¯
t =
d · (Y − C).
For applications that compute a large number of distances, it might be important
to make the squared distance calculations as fast as possible. If the direction vector
d is not unit length, then a division occurs in the formulas. A space-time trade-off
can be made to avoid the division. If memory permits, whether in the parametric
or standard form, the quantity 1/
d
2
can be precomputed and stored with the line
segment. If memory is not readily available, then the division can be deferred until
absolutely needed. For example, in the standard form the algorithm to defer the
division is
float SquaredDistance(Point Y, Segment S)
{
Point D = S.P1 - S.P0;
Point YmP0=Y-S.P0;
float t = Dot(D, YmP0);
if (t <= 0) {
// P0 is closest to Y
return Dot(YmP0, YmP0);
}
float DdD = Dot(D, D);
if (t >= DdD) {
// P1 is closest to Y
Point YmP1=Y-S.P1;
return Dot(YmP1, YmP1);
}
// closest point is interior to segment
return Dot(YmP0, YmP0)-t*t/DdD;
}
