Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

134 Chapter 4 Matrices, Vector Algebra, and Transformations
P
Q
T(P)
T(Q)
u
T(w)
w
u
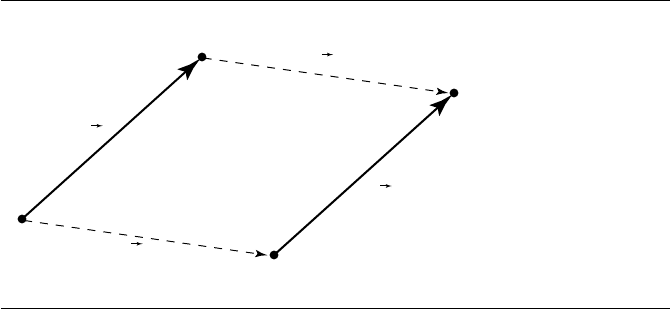
Figure 4.9 Translation.
4.7.2 Translation
Figure 4.9 shows a translation transform—P is an arbitrary point, w is an arbitrary
vector, and u is the translation vector, having coordinates [
u
1
u
2
... u
n
0
].
The affine frame is defined by basis vectors v
i
and origin O.LetQ be such that
Q − P =w.Let’sseehowP translates. Clearly,
T(P)= P +u
To see what the last row in our transformation matrix is, we need to understand how
the origin is translated; if we apply T to O,wehave
T(O) = O +w
=w +O
= (u
1
v
1
+ u
2
v
2
+···+u
n
v
n
) + O
Now, how does the translation transformation affect vectors? Again, we have
T (Q) = Q +u
As points P and Q are translated by the same vector, and that vector is, of course,
parallel to itself, we can see, intuitively, that T(w) is also parallel to w and of the
same length. By the definition of vector equality (see Section 3.1.1), then,
T(w) =w
Of course, this is what we’d expect: vectors are defined as being independent of
position (as they only define a direction), and so translating them about should not
4.7 Vector Geometry of Affine Transformations 135
affect them. This can be shown formally:
T
w
= T
(
Q − P
)
by definition of point subtraction
= T
(
Q
)
− T
(
P
)
by definition of T
=
P +w
−
P +w
by definition of translation of vectors and points
= P −P by Equation 3.3
=w
Translation doesn’t modify orientation or length of vectors, and of course this
includes the basis vectors; that is, the first three rows of the matrix representation of
T are just the coefficients that yield the original basis vectors. If the coordinates of
point P are [p
1
p
2
···p
n
], w e h ave
T
(
P
)
=
[
p
1
p
2
··· p
n
1
]
T
v
1
T
v
2
.
.
.
T
v
n
T
O
=
[
p
1
p
2
··· p
n
1
]
v
1
v
2
.
.
.
v
n
O +u
=
[
p
1
p
2
··· p
n
1
]
T
v
1
v
2
.
.
.
v
n
O
Using the definition of matrix multiplication, we can see that
T =
10··· 00
01··· 00
.
.
.0100
00··· 10
u
1
u
2
··· u
n
1
=
I
0
T
u 1
which can be seen diagrammatically in Figure 4.10.
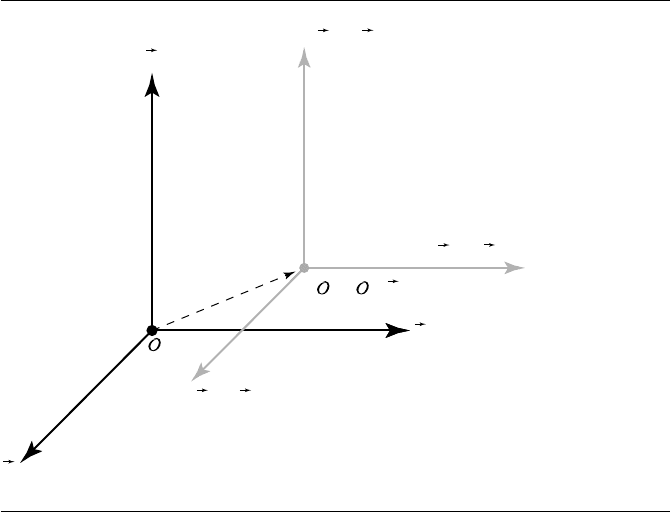
136 Chapter 4 Matrices, Vector Algebra, and Transformations
v
1
v
2
v
3
T(v
3
) = v
3
T( ) = + u
T(v
1
) = v
1
T(v
2
) = v
2
Figure 4.10 Translation of a frame.
4.7.3 Rotation
Rotation in 3D is frequently treated only as rotation about one of the coordinate axes
with general rotation treated as a reduction to this simpler case (using translation).
Here we describe the simple case but then go on to show how the general case can be
solved directly and more efficiently.
Simple Cases
The most general specification for a rotation is given by an arbitrary center of ro-
tation, an arbitrary axis, and an angle. However, we’ll wait to address this until we
describe the simplest form: the frame’s origin is the center of rotation, and the axis
of rotation is one of the frame’s basis vectors (“rotation about a coordinate axis”).
Building up a matrix for this can be done directly, using only vector algebra princi-
ples (Figure 4.11). We’ll describe how to build the matrix T for a rotation about the
z-axis by the angle θ. For the 3D case we’ll be discussing, the notation for the elements
of T is as follows:
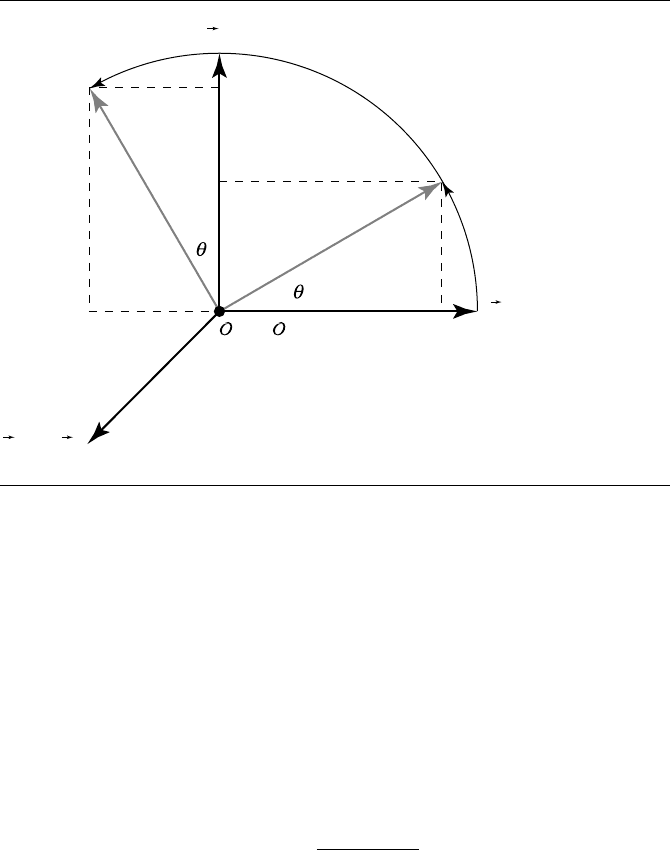
4.7 Vector Geometry of Affine Transformations 137
v
1
a
1, 2
v
2
a
2, 2
a
2, 1
a
1, 1
T(v
1
)
T(v
2
)
v
3
= T(v
3
)
= T( )
Figure 4.11 Simple rotation of a frame.
T =
a
1,1
a
1,2
a
1,3
0
a
2,1
a
2,2
a
2,3
0
a
3,1
a
3,2
a
3,3
0
0001
First, consider the effect of the transformation on the x-axis; that is, v
1
. We know
from our discussion of the dot product (Section 3.3.1) that T(v
1
) can be decomposed
into T(v
1
)
and T(v
1
)
⊥
(relative to v
1
). Using the definition of the dot product
(Equations 3.5, 3.6, and 3.7), we have
cos θ =
T(v
1
) ·v
1
T(v
1
)v
1
but T(v
1
)=1 and v
1
=1, so we have
cos θ = T(v
1
) ·v
1
Recalling that the dot product projects T(v
1
) onto v
1
, we can conclude that a
1,1
=
cos θ.
138 Chapter 4 Matrices, Vector Algebra, and Transformations
We can compute a
1,2
similarly: the angle between T(v
1
) and v
2
(the y-axis) is
π/2 − θ. If we apply the same reasoning as we just used for the x-axis, we see that
a
1,2
= cos(π/2 −θ). From trigonometry we know that cos(π/2 − θ) = sin θ ,sowe
can conclude that a
1,2
= sin θ. Thus, we have the transformed coordinates of basis
vector v
1
:
T(v
1
) =
[
cos θ sin θ 00
]
We can follow the same sort of reasoning for computing a
2,1
and a
2,2
, the coordinates
of T(v
2
) (the image of the y-axis under the rotation transformation T ). The projec-
tion of T(v
2
) onto v
1
is − cos(π/2 − θ) (negative because it points in the opposite
direction as v
1
; see Equation 3.4), and so we can conclude that a
2,1
=−sin θ .The
projection (dot product) of T(v
2
) onto v
2
gives us a
2,2
= cos θ, and so we have the
transformed coordinates of basis vector v
1
:
T(v
2
) =
[
− sin θ cos θ 00
]
Next, we consider what the matrix must do to the z-axis; again, nothing:
T(v
3
) =v
3
=
[
0010
]
Finally, consider what the transformation must do to the origin; that is, nothing:
T(O) = O
=
[
0001
]
So, our matrix for the rotation is formed by simply taking the images of the basis
vectors and origin under T as the rows:
T
z
(θ) =
cos θ sin θ 00
− sin θ cos θ 00
0010
0001
For rotation about the x-ory-axis, the same sort of reasoning will produce the
following simple rotation matrices:
T
x
(θ) =
10 00
0cosθ sin θ 0
0 − sin θ cos θ 0
00 01
4.7 Vector Geometry of Affine Transformations 139
and
T
y
(θ) =
cos θ 0 − sin θ 0
01 0 0
sin θ 0cosθ 0
00 0 1
Of course, these values can be arrived at via purely trigonometric reasoning, also
exploiting the fact that the basis vectors are orthonormal.
General Rotation
While individual rotations of points about the basis vectors (the “coordinate axes”)
may be a part of any graphics application, the general case is for a rotation by some
angle about an arbitrarily oriented axis. That being the case, most graphics texts then
go on to explain how you construct the matrix for a general rotation by decomposing
it (in a rather complex fashion) into a sequence of individual steps—translation of a
point on the rotation axis to the origin, determination of the three different angles of
rotation about each coordinate axis, and translation to “undo” the first translation.
The matrix for each of these steps is computed, and the final matrix representing the
general rotation is created by multiplying all of these matrices together.
This conventional approach can be shown to “work,” in that you can be convinced
that the matrix “does the right thing,” but the process is quite complex and results
in a matrix that’s essentially a “black box” from an intuitive standpoint—that is,
there is provided no understanding of the properties or characteristics of the rotation
matrix.
In this section, we’ll show how a general rotation can be defined in terms of
(coordinate-free) vector algebra and how this approach allows us to construct a ro-
tation matrix directly (i.e., as opposed to breaking it down into a sequence of trans-
lations and Euler rotations), in a way that we hope will leave you with an intuitive
understanding of the structure and properties of a rotation matrix. In short, we wish
to show why a general rotation matrix is the way it is, rather than just how you can
construct one using ad hoc trigonometric operations.
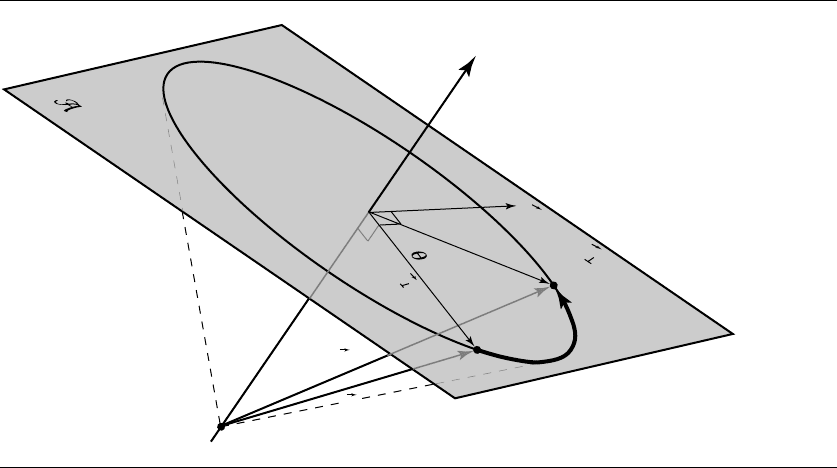
Figure 4.12 shows the general case of rotation of points and vectors about an
arbitrary axis. That figure, and the one following it, are a bit complex, so here are
the definitions of the symbols:
Q, ˆu point and unit vector defining the axis of rotation
θ angle of rotation
P point to be rotated
T(P) rotated point
v vector to be rotated
140 Chapter 4 Matrices, Vector Algebra, and Transformations
P
Q
T(P)
T(v)
v
û
v
w = û ⫻ v
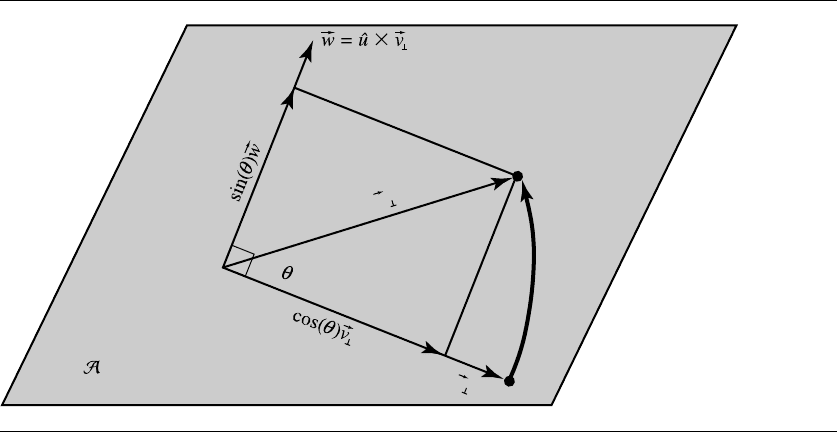
Figure 4.12 General rotation.
T(v) rotated vector
A plane perpendicular to ˆu
v
⊥
projection of v on A
We’re considering a rotation about a (unit) vector ˆu, defining, along with Q,an
axis of rotation, and an angle θ defining a (right-hand rule) counterclockwise rota-
tion about it. For convenience, select vector v as P − Q so we can use one diagram
for discussion of rotation of points and rotation of vectors. Recall our discussion in
Section 3.3.1, where we showed that a vector can be broken down into its parallel
and perpendicular components, relative to another vector; here we project v onto ˆu,
yielding us v
and v
⊥
. Note that we can draw v as originating at Q on the rotation axis
because vectors are position independent, and drawing it there makes the diagrams
easier to understand.
To make the rest of this easier to see, refer to Figure 4.13, which shows the plane
A perpendicular to ˆu and containing P = Q +v. With this in hand, we can make
the following assertions:
T
v
⊥
= T
v
⊥
= (cos θ)v
⊥
+ (sin θ)ˆu ×v
⊥
(4.25)
4.7 Vector Geometry of Affine Transformations 141
P
T(P)
v
T(v)
Figure 4.13 General rotation shown in the plane A perpendicular to ˆu and containing P .
and
T
v
= T
v
=v
(4.26)
Because v =v
+v
⊥
and T is a linear transformation, we have
T
v
= T(v
) + T(v
⊥
)
We can substitute Equations 4.25 and 4.26 and expand these using the definitions of
parallel and perpendicular vector components, and we get
T
v
= (v ·ˆu) + (cos θ)(v −(v ·ˆu) ˆu) + (sin θ)(ˆu × (v −(v ·ˆu) ˆu))
= (cos θ)v +(1 − cos θ)(v ·ˆu) ˆu + (sin θ)(ˆu ×v)
This formulation is variously known as the rotation formula or Rodriguez’s formula
(Hecker 1997).
Finally, we can use this formula, along with the definition of adding points and
vectors, to find the formula for rotation of a point:
142 Chapter 4 Matrices, Vector Algebra, and Transformations
T(P)= Q + T
(
P − Q
)
= Q + T
v
= Q + (cos θ)v +(1 − cos θ)(v ·ˆu) ˆu + (sin θ)(ˆu ×v)
Now, if we want the matrix representation of this, recall that we’re going to be “pulling
out” the vector from these equations. Let
T
u,θ
= (cos θ)I + (1 − cos θ)u ⊗u + (sin θ)˜u
be the upper left-hand submatrix of T (recall that ˜u is the skew-symmetric matrix
for the cross product operation involving ˆu, as discussed in Section 4.4.2). Then, our
total transform is now
T =
T
u,θ
0
T
Q − QT
u,θ
1
The submatrix T
u,θ
should be easy to understand: it’s just the (linear) transform
of the vector v. The bottom row, however, may require a little explanation. First,
observe that this bottom row only affects the transformation of points because the
last component of the matrix representation of a vector is 0. Clearly, vectors will be
properly transformed by T because T
u,θ
, which represents the linear transformation
component of the rotation, affects the calculation, but the bottom row does not. This
is tantamount to assuming the point Q is at the origin. Thus, if Q is not at the origin,
then we must translate by the difference between Q and its rotated counterpart.
4.7.4 Scaling
We’re going to treat scaling as two separate cases: uniform versus nonuniform. Recall
that earlier (Section 3.3), we claimed that certain operations on points are somewhat
“illegitimate”; scaling a point seems to be one of these operations. As we pointed
out, scaling only means something when it’s relative to some frame of reference. We
could, then, define scaling points relative to the affine frame’s origin; however, a more
general approach could be to define scaling relative to an arbitrary origin and scaling
vector (a vector whose components are the scaling factor in each dimension).
Simple Scaling
The simplest form of scaling is to use the frame’s origin as the center of scaling. Scal-
ing may be uniform or nonuniform: in the uniform case, a single scaling parameter
is applied to each of the basis vectors, or separate scaling parameters for each basis
vector.
4.7 Vector Geometry of Affine Transformations 143
v
1
v
2
v
3
T(v
1
) = s
x
v
1
T(v
3
) = s
z
v
3
T(v
2
) = s
y
v
2
= T( )
Figure 4.14 Scaling a frame.
Again, we proceed by considering in turn what the scaling transformation T does
to each of the basis vectors (Figure 4.14). We’ll assume a separate scaling parameter
for each, noting that a uniform scale simply has each of these specified with the same
value. For v
1
(the x-axis) we apply Equation 4.6 to the matrix representation of the
x-axis:
T(v
1
) = s
x
v
1
= s
x
[
1000
]
=
[
s
x
000
]
and similarly for the y-axis:
T(v
2
) = s
y
v
2
= s
y
[
0100
]
=
[
0 s
y
00
]
