Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

124 Chapter 4 Matrices, Vector Algebra, and Transformations

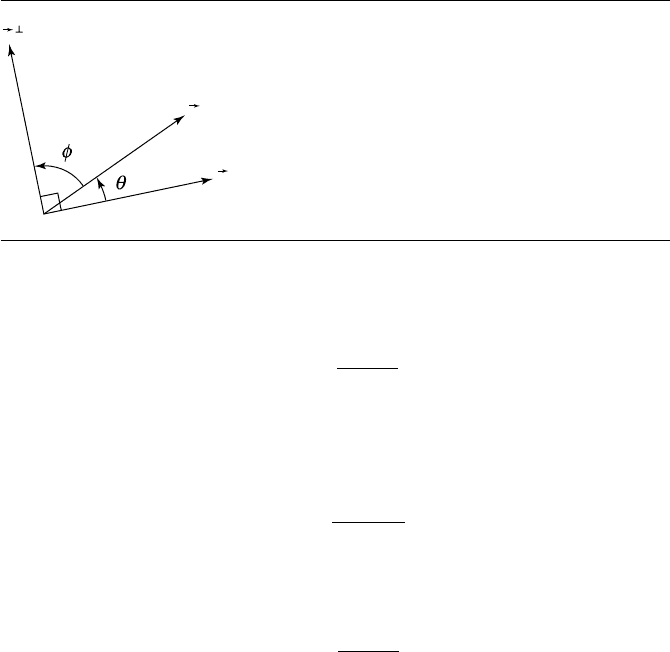
Figure 4.4 The perp dot product reﬂects the signed angle between vectors.

cos θ =

u ·v

uv

(4.9)

(see Section 3.3.1). So, if we consider the relationship between u

⊥

and v in terms of

the angle between them (as shown in Figure 4.4), we can see that

cos φ =

u

⊥

·v

u

⊥

v

As we proved earlier, u

⊥

=u, so the above can be rewritten as

cos φ =

u

⊥

·v

uv

(4.10)

u

⊥

·v =uvcos φ (4.11)

To carry this further, we note that if θ + φ =π/2, then sin θ =cos φ (we encour-

age you to break out your copy of your preferred symbolic math application program

to verify this). We can see directly from the ﬁgure that indeed θ + φ = π/2, and so

Equation 4.10 can be rewritten as

u

⊥

·v =uvsin θ

It may help if you suppose that the two vectors are normalized, in which case

ˆu

⊥

·ˆv =sin θ (4.12)

4.4 Products of Vectors 125

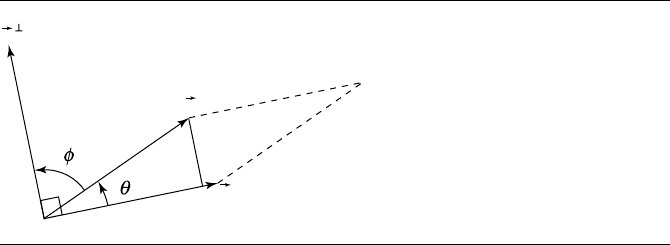
Figure 4.5 The perp dot product is related to the signed area of the triangle formed by two

vectors.

This makes it completely obvious that the perp dot product reﬂects not only the angle

between two vectors but the direction (that is, the sign) of the angle between them.

Contrast this with the relationship between the (usual) dot product of two vectors

and their angle, as shown in Equation 4.9, which indicates the angle between the

vectors, but fails to discriminate the orientation of the angle (i.e., the signed angle).

The second geometric property of the perp dot product can be seen by observing

Figure 4.5. By deﬁnition, sin θ = h/v, so the height of the parallelogram deﬁned

by u and v is h =v sin θ. Its base is, of course, u,sowehave

Area =uv sin θ

Note that the right-hand side of this equation is the same as that of Equation 4.12,

from which we can conclude that the perp dot product of two vectors is equal to

twice the signed area of the triangle deﬁned by the two vectors.

Recall from Section 3.3.1 that the cross product of two vectors (in 3-space) is

related to the area of the parallelogram, so we can now see, as Hill (1994) pointed out,

that the perp dot product can be viewed as the 2D analog of the 3D cross product.

Another way of arriving at this is to simply write out the perp dot product in

terms of its components:

u

⊥

·v =−u

+ u

= u

− u



If we consider u and v to be 3D vectors that are embedded in the z = 0 plane, then

the above can be seen to be exactly the triple scalar product (u ×v) · [

001

126 Chapter 4 Matrices, Vector Algebra, and Transformations

As shown in Equation 3.13 in Section 3.3.1, the triple scalar product is related to

the determinant formed by the three vectors as rows of a matrix, which deﬁnes the

volume of the parallelepiped. As the height in our case is 1, this is also related to the

area.

Properties

We conclude by enumerating and proving several properties of the perp dot product

where they differ from the usual dot product properties:

i. u

⊥

·v =−v

⊥

·u. The usual dot product rule is u ·v =v ·u.

ii. v

⊥

·v =0. The usual dot product rule is v ·v =v

iii. u

⊥

·v =uvsin θ. The usual dot product rule is u ·v =uv cos θ .

4.5 Matrix Representation of Afﬁne

Transformations

In Section 2.1.1, we showed that a matrix multiplication can be interpreted in any

one of several fashions—as a change of coordinates, a transformation of a plane onto

itself, or as transformation from one plane to another. In Section 4.6 we discuss how,

in general, we can construct a matrix that performs a change-of-basis transforma-

tion. In this section, we discuss how to construct a matrix that performs an afﬁne

transformation on points and vectors.

Suppose we have two afﬁne spaces A and B, and with each we have arbitrarily

chosen frames F

(v

, v

, ..., v

, O

) and F

( w

, w

, ..., w

, O

), respectively.

If we have an arbitrarily chosen point P , we can describe its position in terms of

(v

, v

, ..., v

, O

) as [

... a

]. If we have an afﬁne transformation T

that maps A to B, then we use the notation T

(

)

to refer to the point resulting from

applying that transformation to the point. This is all very abstract and coordinate-

free, but as we’re now discussing matrix representations (and hence coordinates),

we’d like to be able to ﬁnd the coordinates of T

(

)

relative to



w

, w

, ..., w

, O



respectively.

We showed in Section 4.2 how to represent a point (or vector) in matrix terms,

so we can expand T

(

)



v

+ a

v

+···+a

v

+ O



(4.13)

We can invoke the property of preservation of afﬁne combinations (Equation 3.14)

to rewrite Equation 4.13 as



v



+ a



v



+···+a



v



+ T





4.5 Matrix Representation of Afﬁne Transformations 127

The entities T



v



are, of course, just more vectors, and T





is just a point

(because, by deﬁnition, afﬁne transformations such as T mapvectorstovectors

and points to points). As such, they have a representation (i.e., coordinates)



, c

, ···, c



relative to



w

, w

, ..., w

, O



. We can then write



v



= c

1,1

w

+ c

1,2

w

+···+c

1,n

w



v



= c

2,1

w

+ c

2,2

w

+···+c

2,n

w



v



= c

n,1

w

+ c

n,2

w

+···+c

n,n

w





= c

n+1,1

w

+ c

n+1,2

w

+···+c

n+1,n

w

+ O

With all of this in place, we can now simply construct the matrix T, which

represents the transform T : A −→ B:

(

)

[

··· a

]









v





v





v













[

··· a

]







1,1

w

+ c

1,2

w

+···+c

1,n

w

2,1

w

+ c

2,2

w

+···+c

2,n

w

n,1

w

+ c

n,2

w

+···+c

n,n

w

n+1,1

w

+ c

n+1,2

w

+···+c

n+1,n

w

+ O







[

··· a

]







1,1

1,2

··· c

1,n

2,1

2,2

··· c

2,n

n,1

n,2

··· c

n,n

n+1,1

n+1,2

··· c

n+1,n













w







(4.14)

Of course, the rightmost matrix of the last line in Equation 4.14 is simply the frame

for B, and

128 Chapter 4 Matrices, Vector Algebra, and Transformations

[

··· a

]







1,1

1,2

··· c

1,n

2,1

2,2

··· c

2,n

n,1

n,2

··· c

n,n

n+1,1

n+1,2

··· c

n+1,n







[

··· a

]

T (4.15)

is, by the deﬁnition of matrix multiplication (see Section 2.3.4), simply a point. Taken

together, the matrix product deﬁnes a point in B, which is T(P), whose coordinates

are the elements of the row matrix resulting from multiplying the matrices in Equa-

tion 4.15. We call that (n + 1) × (n + 1) matrix T the matrix representation of the

transformation T .

Notice that the ﬁrst n rows of T are simply the transformed basis vectors of A,

and the last row is the transformed origin. At the end of Section 3.4, we showed

that an afﬁne transformation is completely determined by its operation on n basis

vectors; the observation that the matrix representing a transformation is deﬁned by

the transformation of the coordinates of the basis vectors’ matrix representations is

simply the matrix manifestation of this fact.

4.6 Change-of-Basis/Frame/Coordinate System

As discussed in Section 3.2.5, a point or vector may be represented in different frames

of reference. Put another way, if we have a ﬁxed point in some space, we can choose

any arbitrary frame and determine the coordinates of that point relative to the frame

uniquely. Recall that the computations for this looked rather cumbersome. We now

show how matrices can be conveniently employed in change-of-basis transforma-

tions. Further, by looking at the construction of such matrices from a vector algebra

perspective, the matrix construction is intuitive as well.

In the previous section we showed that a point P =(a

, a

, ..., a

,1) can be rep-

resented in relation to afﬁne frame F

=(v

, v

, ..., v

, O

)

using matrices. If we

have another frame F

= ( w

, w

, ..., w

, O

)

, how do we compute the coordi-

nates of P relative to these basis vectors and origin? (See Figure 4.6.) In Section 3.2.5,

we showed how this works, and we now show the process in terms of matrices.

The previous section showed the way we use matrices to express a point as the

multiplication of a row matrix (consisting of its coordinates) by an (n +1) ×n matrix

(consisting of the basis vectors and origin of the frame). If, then, we have another set

of basis vectors and origin for another frame, the problem consists of computing the

row matrix for P ’s coordinates:

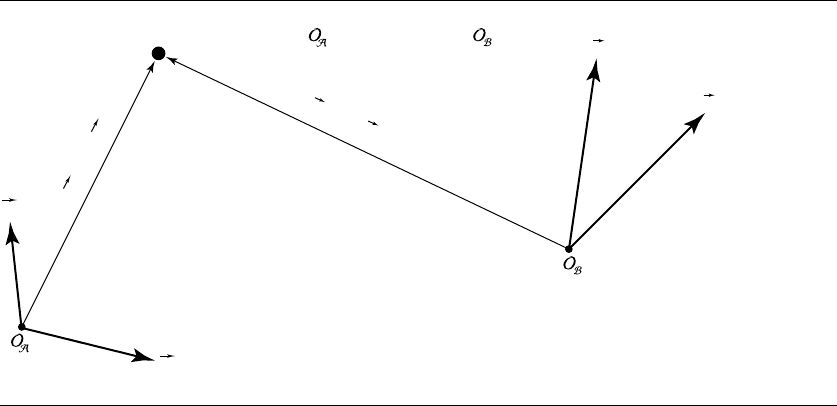
4.6 Change-of-Basis/Frame/Coordinate System 129

P = a

+ a

+ = b

+ b

+ a

+ b

Figure 4.6 Representing P in A and B.

P =

[

··· a

]







v







[

··· b

]







w







(4.16)

which, if we expand the matrix on each side of the equation, yields

[

··· a

]







1,1

1,2

··· v

1,n

2,1

2,2

··· v

2,n

n,1

n,2

··· v

n,n

A,1

A,2

··· O

A,n







[

··· b

]







1,1

1,2

··· w

1,n

2,1

2,2

··· w

2,n

n,1

n,2

··· w

n,n

B,1

B,2

··· O

B,n







(4.17)

130 Chapter 4 Matrices, Vector Algebra, and Transformations

n + 1, 2

n + 1, 1

+ c

n + 1, 2

= c

n + 1, 1

+ c

n + 2, 2

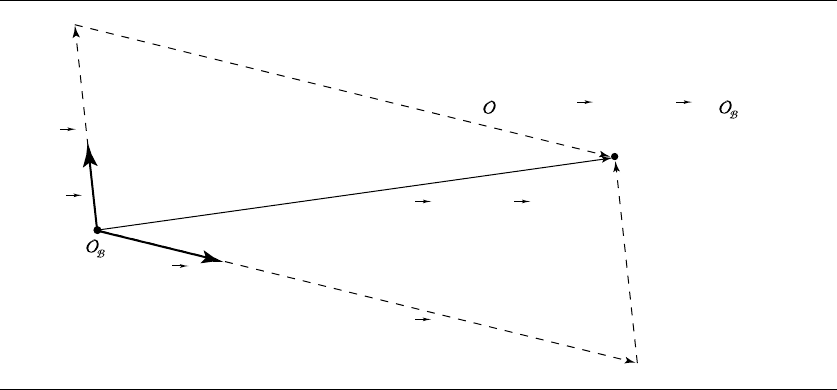
Figure 4.7 Representing O in G.

In Section 3.2.3, we showed how any point (vector) can be represented as a unique

afﬁne combination of basis vectors. Well, we can apply this principle to the vectors



v

, v

, ..., v



and the point O

v

= c

1,1

w

+ c

1,2

w

+···+c

1,n

w

(4.18)

v

= c

2,1

w

+ c

2,2

w

+···+c

2,n

w

(4.19)

v

= c

n,1

w

+ c

n,2

w

+···+c

n,n

w

(4.20)

= c

n+1,1

w

+ c

n+1,2

w

+···+c

n+1,n

w

+ 1 · O

(4.21)

In other words, the c

are the coordinates of the v

and O

, relative to the afﬁne frame



w

, w

, ..., w

, O



(see Figures 4.7 and 4.8, respectively). In terms of the matrix

representation, we can show this as well; we start off by noting that we can write

the right-hand sides of Equations 4.18 through 4.20 and Equation 4.21 in matrix

form:

4.6 Change-of-Basis/Frame/Coordinate System 131

1, 2

1, 1

= c

1, 1

+ c

= c

2, 1

+ c

2, 1

2, 2

Figure 4.8 Representing v

in B.







1,1

w

+ c

1,2

w

+···+c

1,n

w

2,1

w

+ c

2,2

w

+···+c

2,n

w

n,1

w

+ c

n,2

w

+···+c

n,n

w

n+1,1

w

+ c

n+1,2

w

+···+c

n+1,n

w

+ O







(4.22)

If we refer back to the deﬁnition of matrix multiplication (Section 2.3.4), we see we

could rewrite Equation 4.22 as two separate matrices:







1,1

w

+ c

1,2

w

+···+c

1,n

w

2,1

w

+ c

2,2

w

+···+c

2,n

w

n,1

w

+ c

n,2

w

+···+c

n,n

w

n+1,1

w

+ c

n+1,2

w

+···+c

n+1,n

w

+ O







(4.23)







1,1

1,2

··· c

1,n

2,1

2,2

··· c

2,n

n,1

n,2

··· c

n,n

n+1,1

n+1,2

··· c

n+1,n













1,1

1,2

··· w

1,n

2,1

2,2

··· w

2,n

n,1

n,2

··· w

n,n

B,1

B,2

··· O

B,1







132 Chapter 4 Matrices, Vector Algebra, and Transformations

This allows us to rewrite Equation 4.16 as

[

··· a

]







1,1

1,2

··· c

1,n

2,1

2,2

··· c

2,n

n,1

n,2

··· c

n,n

n+1,1

n+1,2

··· c

n+1,n













1,1

1,2

··· w

1,n

2,1

2,2

··· w

2,n

n,1

n,2

··· w

n,n

B,1

B,2

··· O

B,n







[

··· b

]







1,1

1,2

··· w

1,n

2,1

2,2

··· w

2,n

n,1

n,2

··· w

n,n

B,1

B,2

··· O

B,n







(4.24)

which, if we factor out the matrix common to both sides of the equation, yields

[

··· a

]







1,1

1,2

··· c

1,n

2,1

2,2

··· c

2,n

n,1

n,2

··· c

n,n

n+1,1

n+1,2

··· c

n+1,n







[

··· b

]

4.7 Vector Geometry of Afﬁne Transformations

The preceding section showed that we can construct the matrix T for a transforma-

tion T by simply “stacking up” the row matrices representing the transformed basis

vectors and origin. This is all very interesting and elegant, but in practical terms we

must now ask how we do this for each of the fundamental types of afﬁne transforms.

The subsequent sections describe each of these in vector algebra (coordinate-free)

fashion, along with how this translates (so to speak) to a matrix representation. All

we have to do, essentially, is to ﬁgure out what the matrix does to the origin and to

the basis vectors of the afﬁne space (actually, any linearly independent set of vectors,

and any point will do, of course).

4.7 Vector Geometry of Afﬁne Transformations 133

For the simpler transformations, this sort of constructive approach yields a ma-

trix that looks just like the ones given in more conventional treatments (i.e., trans-

lation and uniform scale). The other transformations will appear different because

we’ll be treating them in a more general, vector-algebra-based fashion. For example,

the conventional approach to rotation shows how you construct a matrix that ro-

tates about a basis vector (“coordinate axis”), and then how you can construct, and

then concatenate, a number of such matrices in order to implement a transforma-

tion about an arbitrary axis. In our treatment, we show how to construct the general

rotation matrix directly. To see how the conventional matrices are really just sim-

ple subsets of the general approach, we show what our approach produces for these

restricted subsets; for example, our rotation matrix rotates about an arbitrary axis,

and we show how this leads to a conventional matrix construction if we restrict the

rotation axis to one of the coordinate axes.

4.7.1 Notation

We’re going to be covering the construction of matrices for afﬁne transformations,

using vector algebra methods. In doing so, we’ll ﬁnd it convenient to employ a nota-

tional convention for matrices’ contents in a more “schematic” fashion. You should

understand by now that an (n + 1) ×(n + 1) afﬁne matrix T can be conceptually

broken up into three parts:

1. The n × n upper left-hand submatrix A

2. The (n +1) ×1 right-hand column, which is always of the form [

00··· 1

]

3. The 1 × n bottom row, which is always of the form



b = [

··· b

]

This compartmentalization will be depicted as

T =







1,1

1,2

··· a

1,n

2,1

2,2

··· a

2,n

n,1

n,2

··· a

n,n

··· b











b 1



and is typically called a block matrix.