Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

194 Chapter 6 Distance in 2D
6.2 Point to Polyline
For calculating the distance between a point Y and a polyline L with vertices P
0
through P
n
and line segments S
i
,0≤i<n, whose end points are P
i
and P
i+1
, the
straightforward algorithm is to calculate the minimum of the distances between the
point and the line segments of the polyline:
Distance
2
(Y , L) = min
0≤i<n
Distance
2
(Y , S
i
) (6.7)
Iterating blindly over the line segments can potentially be expensive for polylines with
a large number of segments or for an application with a large number of polylines for
which the distance calculations must be made frequently.
A variation is to use rejection methods that determine that a line segment is not
sufficiently close enough to the test point that it could replace the currently known
minimum distance, µ. The savings in time occurs by avoiding the potential division
that occurs when the closest point to Y on a line segment is interior to that segment.
Let Y = (a, b).Aslongasµ remains the current minimum, any line segment that
is outside the circle with center Y and radius µ is farther away from Y than µ,so
that segment cannot cause an update of µ. Figure 6.4 illustrates this. The segments
S
1
and S
2
are rejected for the full calculation of distance because both are outside the
circleofradiusµ centered at Y . The segment S
3
is not rejected since it intersects
the circle. However, this begs the question since the rejection tests require comput-
ing the distances from the segments to Y , exactly the tests we are trying to avoid!
A faster, but coarser, rejection test uses axis-aligned infinite strips that contain the
circle. Let S
i
=(x
i
, y
i
), (x
i+1
, y
i+1
)be the next segment to be tested. If S
i
is outside
the infinite strip |x − a|≤µ, then it cannot intersect the circle. The rejection test is
therefore
|x
i
− a|≤µ and |x
i+1
− a|≤µ and (x
i
− a)(x
i+1
− a) > 0
The first two conditions guarantee each segment end point is outside the strip. The
last condition guarantees that the end points are on the same side of the strip. Simi-
larly, if S
i
is outside the infinite strip |y − b|≤µ, then it cannot intersect the circle.
The rejection test is
|y
i
− b|≤µ and |y
i+1
− b|≤µ and (y
i
− b)(y
i+1
− b) > 0
Figure 6.4 illustrates this. The segment S
1
, although outside the circle, is not rejected
because it partly lies in each infinite strip. However, S
2
is rejected because it is outside
the vertical strip.
Since square roots should be avoided in the intermediate calculations, an imple-
mentation maintains the squared-distance µ
2
instead of µ. The rejection test must
be restructured accordingly to use µ
2
:
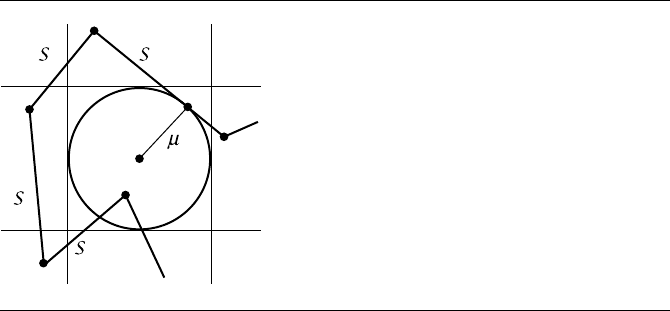
6.2 Point to Polyline 195
Y
1
2
3
0
Figure 6.4 The segment S
0
generated the current minimum distance µ between the polyline
and Y . S
1
and S
2
cannot cause µ to be updated because they are outside the circle
of radius µ centered at Y . Segment S
3
does cause an update since it intersects the
circle. The infinite-strip test does not reject S
1
and S
3
since they lie partly in both
infinite strips, but S
2
is rejected since it is outside the vertical strip. The rectangle test
rejects S
1
and S
2
since both are outside the rectangle containing the circle, but does
not reject S
3
.
|x
i
− a|
2
≤ µ
2
and |x
i+1
− a|
2
≤ µ
2
and (x
i
− a)(x
i+1
− a) > 0
or
|y
i
− b|
2
≤ µ
2
and |y
i+1
− b|
2
≤ µ
2
and (y
i
− b)(y
i+1
− b) > 0
The quantities in the rejection test are also used in the squared-distance calculation,
so these can be temporarily saved in case they are needed later to avoid redundant
calculations. Also, the quantities x
i+1
− a and y
i+1
− b in the current rejection test
become the x
i
− a and y
i
− b values in the next rejection test, so these should be
saved in temporary variables and used later when needed, again to avoid redundant
calculations.
A modification of the rejection test involves testing for intersection between a seg-
ment and the axis-aligned rectangle that contains the circle of radius µ centered at Y .
We can use the method of separating axes discussed in Section 7.7. The improvement
is illustrated by Figure 6.4. The segment S
1
was not rejected by the previous method
because it lies partly in both infinite strips. However, S
1
is rejected by the current
method because it does not intersect the axis-aligned rectangle.
If the segments of the polyline are stored using the symmetric form C +t ˆu,where
C is the center of the segment, ˆu is a unit-length vector, and |t|≤r, then the rejection
test is as follows. Define
3 = C − Y = (3
0
, 3
1
) and ˆu = (u
0
, u
1
). The segment is
rejected (and is outside the box) if any of the tests are true:
196 Chapter 6 Distance in 2D
|3
0
|≥µ + r|u
0
|
|3
1
|≥µ + r|u
1
|
|3
0
u
1
− 3
1
u
0
|≥rµ(|u
0
|+|u
1
|)
Since the square root is being avoided by tracking the value of µ
2
, the three tests
must be slightly revised to use µ
2
:
|3
0
|−r|u
0
|≥0 and (|3
0
|−r|u
0
|)
2
≥ µ
2
|3
1
|−r|u
1
|≥0 and (|3
1
|−r|u
1
|)
2
≥ µ
2
|3
0
u
1
− 3
1
u
0
|
2
≥ r
2
µ
2
(|u
0
|+|u
1
|)
2
Finally, if an application has specific knowledge of the form of its polylines, it
might be possible to organize the polyline with a data structure that helps localize
the calculations. These algorithms, of course, will be specific to the application and
might not work as general tools.
6.3 Point to Polygon
The only difference between measuring distance from a point to a polygon and
measuring distance between a point and a polyline is that the polygon is treated as a
solid object. If the point is inside the polygon, then the distance is zero. If the point is
outside, then for a nonconvex simple polygon without any preprocessing, the point-
to-polyline distance algorithms are applied. See Section 13.3 for the point-in-polygon
containment query.
Some special cases are handled here. We consider the special cases of computing
the distance between a point and a triangle, a rectangle, and an orthogonal frustum,
all polygons being convex. We also mention a couple of methods for computing
distance from a point to a convex polygon.
6.3.1 Point to Triangle
Let Y be the test point, and let the triangle have vertices P
i
,0≤i ≤ 2, that are coun-
terclockwise ordered. If Y is inside the solid triangle, then the distance is defined to
be zero. If Y is outside the solid triangle, then the problem reduces to finding the
closest point on the triangle (as a polyline). The algorithm localizes the search for the
closest point by determining where Y is relative to the triangle. This is more efficient
than just computing distances from the test point to all three triangle edges and se-
lecting the minimum. Figure 6.5 illustrates a few configurations. Figure 6.5(a) shows
a point that is zero distance from the triangle since it is contained in the triangle. Fig-
ure 6.5(b) shows a point that is closest to an edge of the triangle. Figure 6.5(c) shows
a point that is closest to a vertex of the triangle. The solid lines indicate the lines that
contain the edges of the triangles. The dotted lines indicate the perpendicular direc-
tions to the edges. Figure 6.5(d) shows a point that is closest to an edge of the triangle,
6.3 Point to Polygon 197
Y
P
2
P
1
P
0
Y
P
2
P
1
P
0
Y
P
2
P
1
P
0
Y
P
2
P
1
P
0
(a) (b)
(c) (d)
Figure 6.5 Closest point on a triangle to a given point: (a) Dist(Y , T ) = 0; (b) Dist(Y , T ) =
Dist(Y , <P
0
, P
1
>); (c) Dist(Y , T ) = Dist(Y , P
2
); (d) Dist(Y , T ) = Dist(Y , <
P
1
, P
2
>).
but is in the wedge formed by the two (solid) edge-rays with common origin at the
vertex. This example shows that the closest point on the triangle to a Y is determined
by the location of Y in the plane as partitioned by the edge-perpendicular lines at the
vertices, not the edge-lines themselves. In particular, the difference shows up at an
obtuse angle of the triangle.
We present two methods of searching for the closest point. The first method
effectively searches the triangle interior first and the edges second. Its main goal is
to allow at most one division and to do that division only if absolutely necessary. The
trade-off for avoiding the expensive division is more floating-point comparisons. On
current architectures where floating-point addition and multiplication are now faster
than floating-point comparisons, this could be an issue if the application has a large
number of point-triangle distance queries. The second method effectively does the
search in the reverse order, edges first and triangle interior second. Its main goal is to
hope that the closest point is a vertex and is found quickly.

198 Chapter 6 Distance in 2D
Interior-to-Edge Search for a Closest Point
The algorithm uses the parameterized form of the triangle. Let
d
0
= P
1
− P
0
and
d
1
= P
2
− P
0
. The triangle points are X(t
0
, t
1
) = P
0
+ t
0
d
0
+ t
1
d
1
for t
0
≥ 0, t
1
≥ 0,
and t
0
+ t
1
≤ 1. The squared distance between the test point Y and a point X(t
0
, t
1
)
on the triangle is the quadratic function
F(t
0
, t
1
) =X(t
0
, t
1
) − Y
2
=P
0
+ t
0
d
0
+ t
1
d
1
− Y
2
= a
00
t
2
0
+ 2a
01
t
0
t
1
+ a
11
t
2
1
− 2b
0
t
0
− 2b
1
t
1
+ c
where a
00
=
d
0
2
, a
01
=
d
0
·
d
1
, a
11
=
d
1
2
, b
0
=
d
0
· (Y − P
0
), b
1
=
d
1
· (Y − P
0
),
and c =Y − P
0
2
. Although the parameters t
0
and t
1
are subject to the previously
mentioned constraints for the triangle, we consider F(t
0
, t
1
) as a function for all
values of t
0
, t
1
. The set of all pairs (t
0
, t
1
) isreferredtoastheparameter plane.The
global minimum of F occurs when
(0, 0) =
∇F = 2
a
00
t
0
+ a
01
t
1
− b
0
, a
01
t
0
+ a
11
t
1
− b
1
The solution to this system of equations is
¯
t
0
=
a
11
b
0
− a
01
b
1
a
00
a
11
− a
2
01
and
¯
t
1
=
a
00
b
1
− a
01
b
0
a
00
a
11
− a
2
01
The closest triangle point to Y depends on where (
¯
t
0
,
¯
t
1
) lies in the parameter
plane. Figure 6.6 shows the partition of the parameter plane into seven regions by
the lines that contain the triangle edges. If (
¯
t
0
,
¯
t
1
) is in region 0, then Y is inside the
triangle and the distance is zero. For the other regions, notice that the level curves
defined by F(t
0
, t
1
) = λ>0 are ellipses. (For a definition and discussion of level
curves, see Section A.9.1.) If (
¯
t
0
,
¯
t
1
) is in region 1, then the closest triangle point is
on the edge where t
0
+t
1
=1. If there is a value λ
0
> 0 so that the corresponding level
curve is tangent to the edge, then the point of intersection (
ˆ
t
0
,
ˆ
t
1
) yields the closest
point to Y . It is possible that no level curve is tangent to the edge. In this case, the
closest point to Y must correspond to an end point of the edge. Figure 6.7 illustrates
these two cases. The same argument applies when (
¯
t
0
,
¯
t
1
) lies in region 3 or region 5.
Figure 6.7(a) shows tangential contact with an edge. Figure 6.7(b) shows contact with
avertex.
If (
¯
t
0
,
¯
t
1
) is in region 2, three possibilities arise. If there is a λ
0
> 0 so that the cor-
responding level curve is tangent to the edge contained by t
0
+ t
1
= 1, then the point
of intersection (
ˆ
t
0
,
ˆ
t
1
) yields the closest point to Y . If there is no level curve tangent
to that edge, there might be one that is tangent to the edge contained by t
0
= 0. The
point of intersection (0,
ˆ
t
1
) yields the closest point to Y . If no level curves are tan-
gent to the two edges, then the closest point Y is the triangle vertex corresponding to
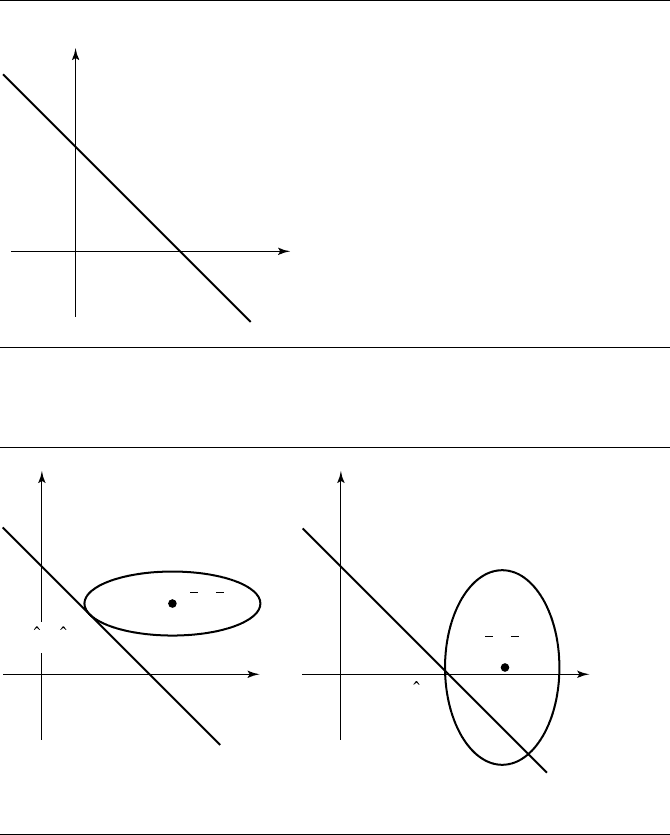
6.3 Point to Polygon 199
t
1
t
0
2
1
3
0
45 6
Figure 6.6 Partitioning of the parameter plane into seven regions.
(t
0
, t
1
)
(1, t
1
)
(t
0
, t
1
)
(t
0
, t
1
)
(a) (b)
Figure 6.7 Contact points of level curves of F(t
0
, t
1
) with the triangle: (a) contact with an edge;
(b) contact with a vertex.
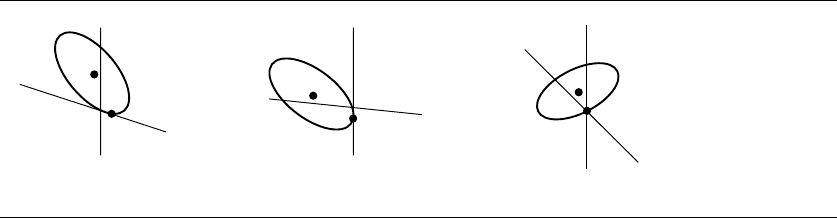
the parameter pair (0, 1). Figure 6.8 illustrates these three cases. The same argument
applies when (
¯
t
0
,
¯
t
1
) lies in region 4 or region 6. Figure 6.8(a) shows tangential con-
tact with one edge. Figure 6.8(b) shows tangential contact with another edge. Figure
6.8(c) shows contact with a vertex.
The following code fragment is structured so that at most one division occurs.
200 Chapter 6 Distance in 2D
2
1
3
0
2
1
3
0
2
1
3
0
(a) (b) (c)
Figure 6.8 Contact points of level curves of F(t
0
, t
1
) with the triangle: (a) contact with an edge; (b) con-
tact with another edge; (c) contact with a vertex.
float SquaredDistance(Point Y, Triangle T)
{
// coefficients of F(t0, t1), calculation of c is deferred until needed
Point D0 = T.P1 - T.P0, D1 = T.P2 - T.P0, Delta=Y-T.P0;
float a00 = Dot(D0, D0), a01 = Dot(D0, D1), a11 = Dot(D1, D1);
float b0 = Dot(D0, Delta), b1 = Dot(D1, Delta);
// Grad F(t0, t1) = (0, 0) at (t0, t1) = (n0 / d, n1 / d)
float n0 = a11 * b0 - a01 * b1;
float n1 = a00 * b1 - a01 * b0;
float d = a00 * a11 - a01 * a01; // theoretically positive
if(n0+n1<=d){
if (n0 >= 0) {
if (n1 >= 0) {
region 0
} else {
region 5
}
} else if (n1 >= 0) {
region 3
} else {
region 4
}
} else if (n0 < 0) {
region 2
} else if (n1 < 0) {
region 6
} else {
region 1
}
}
6.3 Point to Polygon 201
The code block for region 0 just returns zero since Y is inside the triangle and the
squared distance is zero.
// Region 0. Point is inside the triangle, squared distance is zero.
return 0;
If (
¯
t
0
,
¯
t
1
) is in region 5, then the squared-distance function reduces to
G(t
0
) = F(t
0
,0) = a
00
t
2
0
− 2b
0
t
0
+ c
Theproblemnowistocompute
ˆ
t
0
to minimize G(t
0
) for t
0
∈ [0, 1]. This is effec-
tively the same problem as minimizing F, but in one less dimension. The minimum
occurs either at a value where G
= 0 or at one of the end points of the interval. The
solution to G
= 2(a
00
t
0
− b
0
) = 0ist
0
= b
0
/a
00
.Ift
0
∈ (0, 1), then
ˆ
t
0
= b
0
/a
00
.If
t
0
≤ 0, then
ˆ
t
0
= 0. Otherwise t
0
≥ 1 and
ˆ
t
0
= 1. The code block for region 5 is
// Region 5. Minimize G(t0) = F(t0, 0) for t0 in [0, 1]. G’(t0)=0at
// t0 = b0 / a00.
float c = Dot(Delta, Delta);
if(b0>0){
if (b0 < a00) {
// closest point is interior to the edge
returnc-b0*b0/a00; // F(b0 / a00, 0)
} else {
// closest point is end point (t0, t1) = (1, 0)
return a00-2*b0+c; //F(1, 0)
}
} else {
// closest point is end point (t0, t1) = (0, 0)
return c; // F(0, 0)
}
A similar reduction in dimension applies for region 3. The code block is
// Region 3. Minimize G(t1) = F(0, t1) for t1 in [0, 1]. G’(t1)=0at
// t1 = b1 / a11.
float c = Dot(Delta, Delta);
if(b1>0){
if (b1 < a11) {
// closest point is interior to the edge
returnc-b1*b1/a11; // F(0, b1 / a11)
} else {
// closest point is end point (t0, t1) = (0, 1)
202 Chapter 6 Distance in 2D
return a11-2*b1+c; //F(0, 1)
}
} else {
// closest point is end point (t0, t1) = (0, 0)
return c; // F(0, 0)
}
A similar reduction in dimension also applies for region 1, but the algebra is
slightly more complicated. The function to minimize is
G(t
0
) = F(t
0
,1−t
0
) = (a
00
− 2a
01
+ a
11
)t
2
0
+ 2(a
01
− a
11
− b
0
+ b
1
)t
0
+ (a
11
− 2b
1
+ c)
The solution to G
=0ist
0
=(a
11
−a
01
+b
0
−b
1
)/(a
00
−2a
01
+a
11
). Theoretically
the denominator is positive.
// Region 1. Minimize G(t0) = F(t0, 1 - t0) for t0 in [0, 1]. G’(t0)=0at
//t0=(a11-a01+b0-b1)/(a00-2*a01+a11).
float c = Dot(Delta, Delta);
floatn=a11-a01+b0-b1,d=a00-2*a01+a11;
if(n>0){
if(n<d){
// closest point is interior to the edge
return (a11-2*b1+c)-n*n/d; //F(n/d,1-n/d)
} else {
// closest point is end point (t0, t1) = (1, 0)
return a00-2*b0+c; //F(1, 0)
}
} else {
// closest point is end point (t0, t1) = (0, 1)
return a11-2*b1+c; //F(0, 1)
}
Region 2 is more complex to analyze, as shown earlier, since the closest point can
be on one of two edges of the triangle. The pseudocode tests if the closest point is
an interior point of the edge t
0
= 0. If so, the distance is calculated and the function
returns. If not, the closest point on the other edge t
0
+ t
1
= 1 is found, the distance
calculated, and the function returns.
// Region 2. Minimize G(t1) = F(0, t1) for t1 in [0, 1]. If t1 < 1, the
// parameter pair (0, max{0, t1}) produces the closest point. If t1 = 1,
// then minimize H(t0) = F(t0, 1 - t0) for t0 in [0, 1]. G’(t1)=0at
6.3 Point to Polygon 203
// t1 = b1 / a11. H’(t0)=0att0=(a11-a01+b0-b1)/(a00-2*a01
// + a11).
float c = Dot(Delta, Delta);
// minimize on edge t0 = 0
if(b1>0){
if (b1 < a11) {
// closest point is interior to the edge
returnc-b1*b1/a11; // F(0, b1 / a11)
} else {
// minimize on the edge t0 + t1 = 1
floatn=a11-a01+b0-b1d=a00-2*a01+a11;
if(n>0){
if(n<d){
// closest point is interior to the edge
return (a11-2*b1+c)-n*n/d; //F(n/d,1-n/d)
} else {
// closest point is end point (t0, t1) = (1, 0)
return a00-2*b0+c; //F(1, 0)
}
} else {
// closest point is end point (t0, t1) = (0, 1)
return a11-2*b1+c; //F(0, 1)
}
}
} else {
// closest point is end point (t0, t1) = (0, 0)
return c; // F(0, 0)
}
The pseudocode for region 6 has a similar implementation:
// Region 6. Minimize G(t0) = F(t0, 0) for t0 in [0, 1]. If t0 < 1, the
// parameter pair (max{0, t0}, 0) produces the closest point. If t0 = 1,
// then minimize H(t1) = F(t1, 1 - t1) for t1 in [0, 1]. G’(t0)=0at
// t0 = b0 / a00. H’(t1)=0att1=(a11-a01+b0-b1)/(a00-2*a01
// + a11).
float c = Dot(Delta, Delta);
// minimize on edge t1 = 0
if(b0>0){
if (b0 < a00) {
