Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

204 Chapter 6 Distance in 2D

// closest point is interior to the edge

returnc-b0*b0/a00; // F(b0 / a00, 0)

} else {

// minimize on the edge t0 + t1 = 1

floatn=a11-a01+b0-b1,d=a00-2*a01+a11;

if(n>0){

if(n<d){

// closest point is interior to the edge

return (a11-2*b1+c)-n*n/d; //F(n/d,1-n/d)

} else {

// closest point is end point (t0, t1) = (1, 0)

return a00-2*b0+c; //F(1, 0)

}

} else

// closest point is end point (t0, t1) = (0, 1)

return a11-2*b1+c; //F(0, 1)

}

} else {

// closest point is end point (t0, t1) = (0, 0)

return c; // F(0, 0)

}

Finally, the pseudocode for region 4 is

// Region 4. Minimize G(t0) = F(t0, 0) for t0 in [0, 1]. If t0 > 1, the

// parameter pair (min{1, t0}, 0) produces the closest point. If t0 = 0,

// then minimize H(t1) = F(0, t1) for t1 in [0, 1]. G’(t0)=0at

// t0 = b0 / a00. H’(t1)=0att1=b1/a11.

float c = Dot(Delta, Delta);

// minimize on edge t1 = 0

if (b0 < a00) {

if(b0>0){

// closest point is interior to edge

returnc-b0*b0/a00; // F(b0 / a00, 0)

} else {

// minimize on edge t0 = 0

if (b1 < a11) {

if(b1>0){

// closest point is interior to edge

returnc-b1*b1/a11; // F(0, b1 / a11)

6.3 Point to Polygon 205

} else {

// closest point is end point (t0, t1) = (0, 0)

return c; // F(0, 0)

}

} else {

// closest point is end point (t0, t1) = (0, 1)

return a11-2*b1+c; //F(0, 1)

}

} else {

// closest point is end point (t0, t1) = (1, 0)

return a00-2*b0+c; //F(1, 0)

}

Interior-to-Edge Search Time Analysis

The operation counts for the pseudocode are presented here to provide best-case

and worst-case performance of the code. We count additions A; multiplications M;

divisions D; comparisons of two ﬂoating-point numbers C

, neither known to be

zero; and comparisons of a ﬂoating-point number to zero C

. The comparisons are

partitioned this way because ﬂoating-point libraries tend to support a test of the sign

bit of a number that is faster than a general ﬂoating-point comparison.

The block of code in

SquaredDistance that occurs before the set of conditional

statements, but including the sum in the ﬁrst conditional, requires 15 additions

and 16 multiplications. Each region block incurs the cost of these operations. Table

6.1 shows the best-case and worst-case operation counts for the various regions. As

expected because of the design, the best case for region 0 requires the least amount

of time per point. The worst case for region 6 requires the most amount of time per

point.

Edge-to-Interior Search for a Closest Point

This method, proposed by Gino van den Bergen in a post to the newsgroup

comp.graphics.algorithms, is an attempted speedup by computing distance to edges

ﬁrst and hoping that a common vertex for two edges is the closest point. The ar-

gument in that post is that intuitively this method should perform better than the

previous one when Y is far from the triangle. The basis is that if you were to select a

large bounding box for the triangle, and if the test points are uniformly distributed in

that box, the probability that a vertex is closest to a test point is much larger than the

probability that an edge point is closest to a test point or that the test point is interior

to the triangle. To motivate this, consider a triangle with vertices (0, 0), (1, 0), and

206 Chapter 6 Distance in 2D

Table 6.1 Operation counts for point-to-triangle distance calculation using the interior-to-

edge approach.

Region/count AMDC

0, best 15 16 0 1 2

0, worst 15 16 0 1 2

1, best 23 20 0 1 3

1, worst 24 21 1 2 3

2, best 16 18 0 1 2

2, worst 24 21 1 3 3

3, best 16 18 0 1 3

3, worst 17 19 1 2 3

4, best 18 19 0 2 2

4, worst 17 19 1 3 4

5, best 16 18 0 1 3

5, worst 17 19 1 2 3

6, best 16 18 0 1 3

6, worst 24 21 1 3 4

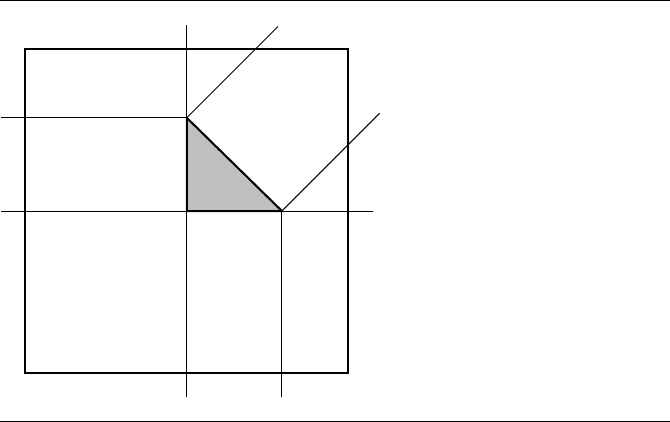
(0, 1) and a bounding box [−r, r]

,wherer ≥1. Figure 6.9 illustrates these and shows

the regions of points closest to vertices and to edges.

Regions V

, V

, and V

are the sets of points closest to (0, 0), (1, 0), and (0, 1),re-

spectively. Regions E

, E

, and E

are the sets of points closest to edges (0, 0), (1, 0),

(1, 0), (0, 1), and (0, 1), (0, 0), respectively. Region T is the triangle interior. The

area of T is A

= 1/2. The total area of the edge regions is A

= 4r − 3/2. The to-

tal area of the vertex regions is A

= 4r

− 4r + 1. Clearly A

for sufﬁciently

large r since A

is quadratic in r, but A

is only linear in r. Therefore, for sufﬁciently

large r, a randomly selected point in the rectangle has the largest probability of being

in a vertex region. It makes sense in this case to have an algorithm that tests vertices

ﬁrst for closeness to a test point.

However, now consider small r.Ifr =1, the only vertex region with positive area

is V

and has area A

= 1.TheedgeregionareaisA

= 5/2 >A

.IngeneralA

≥

for 1 ≤ r ≤ 1 +

√

6/4

1.612. For this range of r values, a randomly selected

point in the rectangle has the largest probability of being in an edge region. The

chances that the actual distribution of the test points in an application are uniformly

distributed in the sense mentioned above is small, so the method for measuring

distance from a point to a triangle is best determined by testing your own data with

these algorithms.

6.3 Point to Polygon 207

–r r

–r

Figure 6.9 A triangle, a bounding box of the triangle, and the regions of points closest to vertices

and to edges.

The pseudocode for the current algorithm is listed below. The code indicates that

the closest triangle point to the test point is returned. The distance to the test point

can be calculated from this.

float SquaredDistance (Point Y, Triangle T)

{

// triangle vertices V0, V1, V2, edges E0=<V0, V1>, E1=<V1, V2>, E2=<V2, V0>

// closest point on E0 to P is K0 = V0 + t0 * (V1 - V0) for some t0 in [0, 1]

float t0 = ParameterOfClosestEdgePoint(P, E0);

// closest point on E1 to P is K1 = V1 + t1 * (V2 - V1) for some t1 in [0, 1]

float t1 = ParameterOfClosestEdgePoint(P, E1);

if (t0 == 0 and t1 == 0) // closest point is vertex V1

return SquaredLength(Y - V1);

// closest point on E2 to P is K2 = V2 + t2 * (V0 - V2) for some t2 in [0, 1]

float t2 = ParameterOfClosestEdgePoint(P, E2);

if (t1 == 0 and t2 == 0) // closest point is vertex V2

return SquaredLength(Y - V2);

208 Chapter 6 Distance in 2D

if (t0 == 0 and t2 == 0) // closest point is vertex V0

return SquaredLength(Y - V0);

//Y=c0*V0+c1*V1+c2*V2forc0+c1+c2=1

GetBarycentricCoordinates(Y, V0, V1, V2, c0, c1, c2);

if (c0 < 0) // closest point is K1 on edge E1

return SquaredLength(Y - (V1 + t1 * (V2 - V1)));

if (c1 < 0) // closest point is K2 on edge E2

return SquaredLength(Y - (V2 + t2 * (V0 - V2)));

if (c2 < 0) // closest point is K0 on edge E0

return SquaredLength(Y - (V0 + t0 * (V1 - V0)));

return 0; // Y is inside triangle

}

The function ParameterOfClosestEdgePoint(P,E) effectively is what is used in

computing distance from a point to a line segment. The projection of P onto the

line containing the edge V

, V

is K =V

+t(V

−V

),wheret =(P −V

)/V

−



.Ift<0, it is clamped to t = 0 and the closest point to P is V

.Ift>1, it is

clamped to t =1 and the closest point is V

. Otherwise, t ∈[0, 1]and the closest point

is K. The aforementioned function returns the t value. If the function were to be

implemented as described, it involves a division by the squared length of the edge.

At least two calls are made to this function, so the distance calculator would require

a minimum of two divisions, an expensive proposition. A smarter implementation

does not do the division, but computes the numerator n and denominator d of t .If

n<0, t is clamped to 0. If n>d, t is clamped to 1. The numerators and denominators

should be stored as local variables at the scope of the function body for use later in the

barycentric coordinate calculations. If the function returns any of the three vertices,

the division n/d for any of the t-values is never performed.

The function

GetBarycentricCoordinates computes P =



i=0

,where



i=0

= 1. Once c

and c

are known, we can solve c

= 1 − c

− c

. The equa-

tion for P is equivalent to P − V

−V

) + c

−V

). The vector equation

represents two linear equations in the two unknowns c

and c

, a system that can be

solved in the usual manner. The solution, if implemented in a straightforward man-

ner, requires a division by the determinant of the coefﬁcient matrix. The division

is not necessary to perform. The barycentric calculator can return the coordinates

as three rational numbers c

= n

/d having the same denominator. The numerators

and denominator are returned in separate storage. The sign test c

< 0 is equivalent

to n

d<0, so the division is replaced by a multiplication. The conditional test is a

sign test, so the conventional ﬂoating-point comparison can be replaced by a (typi-

cally faster) test of the sign bit of the ﬂoating-point number. Even better would be to

6.3 Point to Polygon 209

avoid the multiplications n

d and have a conditional statement that tests the sign bit

of d. Each clause of the test has three conditionals testing the sign bits of n

If c

< 0, the closest point is on the edge E

and is K

= V

+ t

− V

).The

actual value of t

is needed. If the division n

is deferred by the call to Parame-

terOfClosestEdgePoint

, it must now be calculated in order to compute K

. Similar

arguments apply for the conditional statements for c

and c

More detailed pseudocode that uses the deferred division and avoids the division

in the barycentric calculator is listed below. The return statements are marked for

reference by the section on the time analysis of the pseudocode.

float SquaredDistance (Point Y, Triangle T)

{

// T has vertices V0, V1, V2

// t0 = n0/d0 = Dot(Y - V0, V1 - V0) / Dot(V1 - V0, V1 - V0)

Point D0=Y-V0,E0=V1-V0;

float n0 = Dot(D0, E0);

// t1 = n1/d1 = Dot(Y - V1, V2 - V1) / Dot(V2 - V1, V2 - V1)

Point D1=Y-V1, E1=V2-V1;

float n1 = Dot(D1, E1);

if (n0 <= 0 and n1 <= 0) // closest point is V1

return Dot(D1, D1); // RETURN 0

// t2 = n2/d2 = Dot(Y - V2, V0 - V2) / Dot(V0 - V2, V0 - V2);

Point D2=Y-V2, E2=V0-V2;

float n2 = Dot(D2, E2);

if (n1 <= 0 and n2 == 0) // closest point is V2

return Dot(D2, D2); // RETURN 1

if (n0 <= 0 and n2 <= 0) // closest point is V0

return Dot(D0, D0); // RETURN 2

//D0=Y-V0=V0+c1*(V1-V0)+c2*(V2-V0)=V0+c1

//*E1-c2*E2for

//c0+c1+c2=1,c0=m0/d,c1=m1/d,c2=m2/d

float e00 = Dot(E0, E0), e02 = Dot(E0, E2), e22 = Dot(E2, E2);

float d = e02 * e02 - e00 * e22;

float a = Dot(D0, E2);

float m1 = e02*a-e22*n0;

float m0, m2;

Point D;

210 Chapter 6 Distance in 2D

if(d>0){

if (m1 < 0) { // closest point is V2 + t2 * E2

t2 = n2 / e22;

D=Y-(V2+t2*E2);

return Dot(D, D); // RETURN 3a

}

m2=e00*a-e02*n0;

if (m2 < 0) { // closest point is V0 + t0 * E0

t0 = n0 / e00;

D=Y-(V0+t0*E0);

return Dot(D, D); // RETURN 4a

}

m0=d-m1-m2;

if (m0 < 0) { // closest point is V1 + t1 * E1

t1 = n1/Dot(E1, E1);

D=Y-(V1+t1*E1);

return Dot(D, D); // RETURN 5a

}

} else {

if (m1 > 0) { // closest point is V2 + t2 * E2

t2 = n2 / e22;

D=Y-(V2+t2*E2);

return Dot(D, D); // RETURN 3b

}

m2=e00*a-e02*n0;

if (m2 > 0) { // closest point is V0 + t0 * E0

t0 = n0 / e00;

D=Y-(V0+t0*E0);

return Dot(D, D); // RETURN 4b

}

m0=d-m1-m2;

if (m0 > 0) { // closest point is V1 + t1 * E1

t1 = n1 / Dot(E1, E1);

D=Y-(V1+t1*E1);

return Dot(D, D); // RETURN 5b

}

return 0; // Y is inside triangle, RETURN 6

}

6.3 Point to Polygon 211

Table 6.2

Operation counts for point-to-triangle distance calculation using the

edge-to-interior approach.

Return/count AMDC

011602

1171004

2181206

3a, 3b 29 28 1 8

4a, 4b 30 30 1 9

5a, 5b 33 32 1 10

62726010

Edge-to-Interior Search Time Analysis

The operation counts for the pseudocode are presented here to provide best-case

and worst-case performance of the code. We count additions A, multiplications M,

divisions D, and comparisons of a ﬂoating-point number to zero C

.Nogeneral

comparisons occur in this pseudocode, so C

as deﬁned for the previous algorithm

is always zero. Table 6.2 shows the operation counts for each of the return statements

in the pseudocode. The worst case is assumed for the pair of conditions for the ﬁrst

three return blocks; that is, both sign tests occur with the second one false so that the

return is skipped. The best case is that the condition fails because the ﬁrst sign test in

each condition is false and the return is skipped. The best case is when the function

terminates at the very ﬁrst return statement marked

RETURN 0. The worst case occurs

at the return statements marked

RETURN 5a and RETURN 5b.

Comparing this to the results of the other algorithm whose operation counts are

summarized in Table 6.1, we see that the best case for the edge-to-interior algorithm

(11A,6M,0D,2C

) is faster than the best case for the interior-to-edge algorithm

(15A,16M,0D,1C

,2C

). However, the worst case for the edge-to-interior algo-

rithm (33A,32M,1D,10C

) is slower than the worst case for the interior-to-edge

algorithm (24A,21M,1D,3C

,4C

). To decide which algorithm is the best one for

your application will require either some type of amortized analysis or actual experi-

ments that compute the execution time.

6.3.2 Point to Rectangle

Calculating the distance between a point and a rectangle is less complicated than

that between a point and a triangle. The fact that the polygon has all right angles

greatly simpliﬁes the problem. Within the coordinate system whose axes are aligned

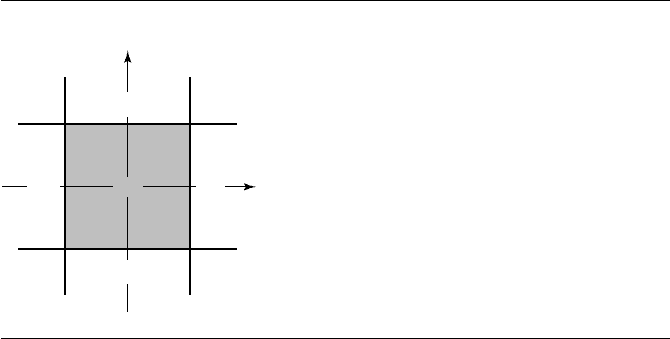
212 Chapter 6 Distance in 2D

MP PPZP

ZM PMMM

MZ ZZ PZ

Figure 6.10 Partitioning of the plane by a rectangle.

with the rectangle sides, the problem decomposes into distance calculations in each

dimension.

Let the test point be Y . The symmetric form for the rectangle is X(t

, t

) =

C +t

ˆu

for |t

|≤e

and |t

|≤e

. The vectors ˆu

are unit length, and C is the

center of the rectangle. This form is used to avoid any divisions at all. The test point

can be transformed to Y =C +s

ˆu

. Setting



 = Y − C,wehaves

=ˆu





and s

=ˆu



. The closest point on the rectangle to Y depends on which of the nine

regions contains (s

, s

) in the (t

, t

) parameter plane. Figure 6.10 illustrates these

regions. If (s

, s

) is in region ZZ, then Y is inside the rectangle and the distance is

zero. If (s

, s

) is in one of regions PZ, ZP, MZ,orZM, then the closest point is the

projection onto the corresponding edge of the rectangle. Otherwise (s

, s

) is in one

of regions PP, PM, MP,orMM. The closest point is the corresponding vertex of the

rectangle.

The skeleton of the pseudocode could be set up to have nested conditional state-

ments, each clause corresponding to one of the nine regions in the partition of the

parameter plane. However, this is not necessary because of the orthogonality of the

rectangle edges. The skeleton is set up to handle each dimension separately.

float SquaredDistance(Point Y, Rectangle R)

{

Point Delta=Y-R.C;

float s0 = Dot(R.U0, Delta), s1 = Dot(R.U1, Delta), sqrDist = 0;

float s0pe0 = s0 + R.e0;

if (s0pe0 < 0) {

sqrDist += s0pe0 * s0pe0;

6.3 Point to Polygon 213

} else {

float s0me0 = s0 - R.e0;

if (s0me0 > 0)

sqrDist += s0me0 * s0me0;

}

float s1pe1 = s1 + R.e1;

if (s1pe1 < 0) {

sqrDist += s1pe1 * s1pe1;

} else {

float s1me1 = s1 - R.e1;

if (s1me1 > 0)

sqrDist += s1me1 * s1me1;

}

return sqrDist;

}

6.3.3 Point to Orthogonal Frustum

A single cone is deﬁned as the set of points whose boundary consists of two rays with

a common origin, called the vertex of the cone. Let the vertex be denoted V . Let the

rays have unit-length directions

and

.Theaxis of the cone is the bisector ray. Let

ˆa be the unit-length direction of the axis. The angle of the cone is the angle θ ∈ (0, π)

between ˆa and either ray direction vector. In this section we restrict our attention to

cones for which θ<π/2. Figure 6.11(a) shows a single cone.

If two parallel lines are speciﬁed that transversely intersect the cone, the convex

quadrilateral that is bounded by the cone and the lines is called a frustum of the cone.

Figure 6.11(b) shows such a frustum. If the lines are perpendicular to the cone axis,

the frustum is said to be an orthogonal frustum. Figure 6.11(c) shows an orthogonal

frustum.

A point X is inside a cone if the angle between X −V and ˆa is smaller than θ.We

can write this constraint in terms of dot products as ˆa · (X −V)≥ cos(θ). A frustum

has additional constraints. If the parallel line closest to the vertex contains the point

P and has a unit-length normal ˆn that points inside the frustum, the line equation

is ˆn · (X −P)= 0. The other line contains a point P + s ˆn for some s>0. The line

equation is ˆn · (X − P)= s. The extra constraints for X to be inside the frustum are

0 ≤ˆn · (X −P)≤ s. If the frustum is orthogonal, ˆn =ˆa.

An orthogonal frustum in two dimensions is the analog of the view frustum that is

used in three dimensions when the camera model is based on perspective projection.

In two dimensions, V plays the role of the eye point, the two parallel lines play the

role of the near and far planes, and the two bounding rays play the role of the left and

right extents of the view frustum. This section provides an algorithm for computing