Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

214 Chapter 6 Distance in 2D
P + sn
n
P
0
1
VVV
(a) (b) (c)
â
ˆ
d
ˆ
d
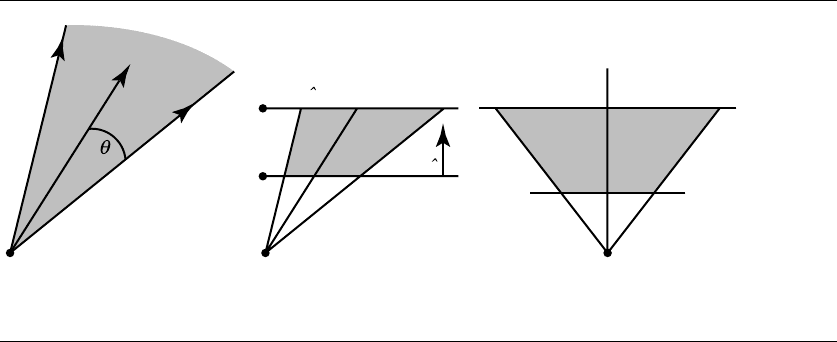
Figure 6.11 (a) An example of a single cone. (b) A frustum of a cone. (c) An orthogonal frustum.
the distance from a point to an orthogonal frustum. The idea is to motivate the same
problem in three dimensions. A distance query for point to frustum is useful for
visibility testing, in particular when the point represents the center of a bounding
sphere for a drawable mesh. If the bounding sphere is outside the frustum, then the
mesh is culled—it does not have to be sent to the renderer for drawing. The bounding
sphere is outside whenever the distance from the sphere center to the frustum is larger
than the sphere radius. Observe that in three dimensions, if the world is constructed
on the xy-plane and if the camera movement is restricted to translation in the xy-
plane and to rotation only about its up-vector, then visibility testing of a bounding
sphere against the left or right frustum planes can be done in 2D by projection onto
the xy-plane. The problem is reduced to testing if a circle is outside a 2D orthogonal
frustum.
The algorithm for computing the distance from a point to an orthogonal frustum
is based on determining the Voronoi regions for the edges and vertices of the frustum.
The region containing the point is computed. The nearest point on the frustum in
that region is also computed. From this the distance can be calculated. The concepts
in 2D generalize in a straightforward manner to 3D and are discussed later in this
book.
The orthogonal frustum has origin E, unit-length direction vector
ˆ
d, and per-
pendicular unit-length vector
ˆ
l. The near line has normal
ˆ
d and contains the point
E +n
ˆ
d for some n>0. The far line has normal
ˆ
d and contains the point E +f
ˆ
d for
some f>n. The four vertices of the frustum are E + n
ˆ
d ± &
ˆ
l for some &>0, and
E + (f/n)(n
ˆ
d ± &
ˆ
l).LetP be the point whose distance to the frustum is required.
The point can be written in the frustum coordinate system as
6.3 Point to Polygon 215
x
1
x
0
R
1
R
0
R
2b
R
2c
R
5
R
4
R
3b
R
3a
R
2a
f
n
f /n
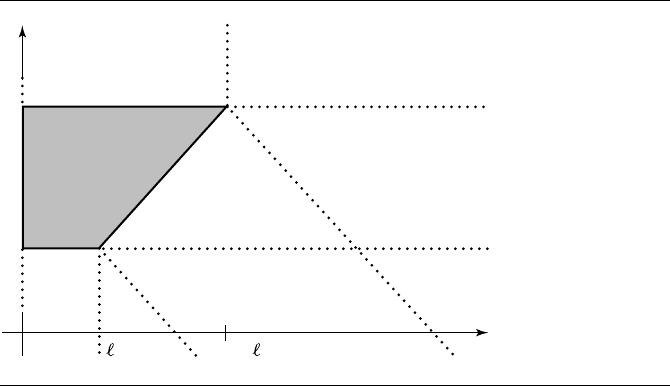
Figure 6.12 Portion of frustum in first quadrant.
P = E +x
0
ˆ
l +x
1
ˆ
d
so x
0
=
ˆ
l ·(P −E) and x
1
=
ˆ
d ·(P −E). It is sufficient to demonstrate the construc-
tion for x
0
≥0. For if x
0
< 0, a reflection can be made by changing the sign on x
0
, the
closest point can be calculated, then a reflection on that point yields the closest point
to the original. Figure 6.12 shows the portion of the frustum in the first quadrant.
The Voronoi region boundaries are dotted. Region R
0
contains those points in-
side the frustum. Region R
1
contains those points closest to the top edge of the frus-
tum. Region R
2
contains those points closest to the vertex (f &/n, f)of the frustum.
That region is split into three subregions based on
ˆ
d component being larger than f ,
between n and f , or smaller than n. Region R
3
contains those points closest to the
slanted edge of the frustum. That region is split into two subregions based on
ˆ
d com-
ponent being between n and f or smaller than n. Region R
4
contains those points
closest to the vertex (&, n) of the frustum. Finally, region R
5
contains those points
closest to the bottom edge of the frustum.
The pseudocode for determining the Voronoi region for (x
0
, x
1
) is
if (x1 >= f) {
if(x0<=f*l/n)
point in R1;
else
point in R2a;
} else if (x1 >= n) {
216 Chapter 6 Distance in 2D
t = Dot((n, -l), (x0, x1));
if (t <= 0)
point in R0;
else {
t = Dot((l, n), (x0, x1));
if (t <= Dot((l, n), (f*l/n,f)))
point in R3a;
else
point in R2b;
}
} else {
if (x0 <= l )
point in R5;
else {
t = Dot((l, n), (x0, x1));
if (t <= Dot((l, n), (l, n)))
point in R4;
else if (t <= Dot((l, n), (f*l/n,f)))
point in R3b;
else
point in R2c;
}
}
The closest point to (x
0
, x
1
) in R
1
is (x
0
, f). The closest point in R
2
is (f &/n, f).
The closest point in R
4
is (&, n). The closest point in R
5
is (x
0
, n). Region R
3
requires
projecting out the (n, −&) component from (x
0
, x
1
). The closest point is (x
0
, x
1
) −
[(nx
0
− &x
1
)/(&
2
+ n
2
)](n, −&).
6.3.4 Point to Convex Polygon
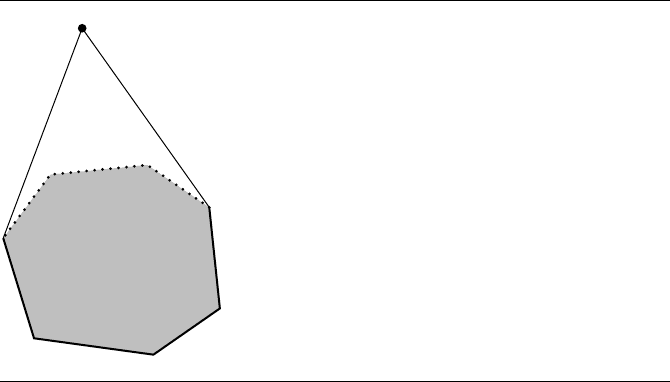
In the special case of a convex polygon, not all point-to-segment tests need to be
made while searching for the minimum distance between the point and edges of the
polygon. Only those edges that are visible to the point X must be considered. Figure
6.13 illustrates the idea.
Assuming that each edge P
i
, P
i+1
has an associated normal vector n
i
that points
to the interior of the polygon, an edge is visible only if n
i
· (X − P
i
) ≥ 0. By test-
ing this dot product first, and if negative, the potential division that occurs in the
point-to-segment distance calculation is avoided. Moreover, a further reduction in
calculations is attained by checking if the next point-to-segment distance is larger
than the current one. If the distance to the current edge is smaller or equal to the
distance from the two neighboring edges, then the current distance is the minimum
distance to the polygon boundary.
6.4 Point to Quadratic Curve 217
Figure 6.13 Only those edges visible to the test point must be searched for the closest point to
the test point. The three visible edges are dotted. The invisible edges are drawn in
black. The visible edges are in a cone with vertex at the test point and whose sides are
tangent to the convex polygon.
Finally, given a point and a convex polygon, the GJK algorithm described in
Section 6.10 provides a viable alternative to a boundary search algorithm that looks
for a closest feature. The method extends to higher dimensions and to arbitrary
convex objects, not necessarily polygons or polyhedra.
6.4 Point to Quadratic Curve
The general quadratic equation is
Q(X) = X
T
AX + B
T
X + c = 0
where A is a symmetric 2 ×2 matrix, but not necessarily invertible, B isa2×1vector,
and c is a scalar. The parameter is X,a2× 1 vector. Given the curve Q(X) = 0 and
a point Y , we need an algorithm for computing the closest point on the curve to Y .
Geometrically, the closest point X must satisfy the condition that Y − X is normal
to the curve. Figure 6.14 illustrates this. Since the gradient
∇Q(X) is normal to the
curve, Y −X and
∇Q(X) must be parallel and the algebraic condition for the closest
point is therefore
Y − X =t
∇Q(X) = t(2AX +B)
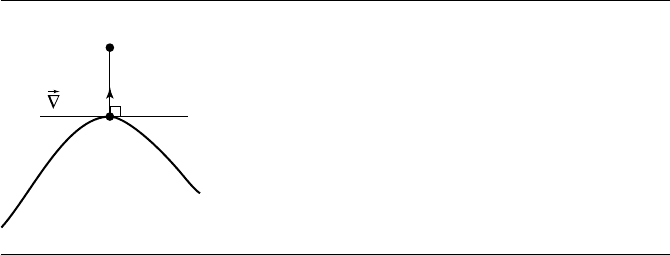
218 Chapter 6 Distance in 2D
Q(X)
X
Y
Figure 6.14 Closest point on a quadratic curve to a given point.
for some scalar t. Therefore,
X = (I + 2tA)
−1
(Y − tB)
where I is the identity matrix. This equation for X can be replaced into the general
quadratic equation to obtain a polynomial in t of at most fourth degree.
Instead of immediately replacing X in the quadratic equation, we can reduce the
problem to something simpler to implement. Factor A using an eigendecomposition
to obtain A = RDR
T
,whereR is an orthonormal matrix whose columns are eigen-
vectors of A and where D =Diag{d
0
, d
1
} is a diagonal matrix whose diagonal entries
are the eigenvalues of A (see Section A.3). Then
X = (I + 2tA)
−1
(Y − tB)
= (RR
T
+ 2tRDR
T
)
−1
(Y − tB)
= [R(I + 2tD)R
T
]
−1
(Y − tB)
= R(I + 2tD)
−1
R
T
(Y − tB)
= R(I + 2tD)
−1
(α − t
β)
where α = (α
0
, α
1
) = R
T
Y and
β = (β
0
, β
1
) = R
T
B. Replacing X in the quadratic
equation and simplifying yields
0 =(α − t
β)
T
(I +2tD)
−1
D(I +2tD)
−1
(α − t
β) +
β
T
(I +2tD)
−1
(α − t
β) + c
The inverse diagonal matrix is (I + 2tD)
−1
=Diag{1/(1 + 2td
0
),1/(1 + 2td
1
)}. Mul-
tiplying through by ((1 + 2td
0
)(1 + 2td
1
))
2
leads to a polynomial of at most fourth
degree, p(t) = p
0
+ p
1
t + p
2
t
2
+ p
3
t
3
+ p
4
t
4
, with
6.5 Point to Polynomial Curve 219
p
0
= c + α
0
β
0
+ α
1
β
1
+ α
2
0
d
0
+ α
2
1
d
1
p
1
= 4[c(d
0
+ d
1
) + α
0
d
1
(β
0
+ α
0
d
0
) + α
1
d
0
(β
1
+ α
1
d
1
)]− (β
2
0
+ β
2
1
)
p
2
= 4[c((d
0
+ d
1
)
2
+ 2d
0
d
1
) + α
0
d
2
1
(β
0
+ α
0
d
0
) + α
1
d
2
0
(β
1
+ α
1
d
1
)]
− β
2
0
(4d
1
+ d
0
) − β
2
1
(4d
0
+ d
1
)
p
3
= 4(d
0
+ d
1
)[4cd
0
d
1
− (β
2
1
d
0
+ β
2
0
d
1
)
p
4
= 4d
0
d
1
[4cd
0
d
1
− (β
2
1
d
0
+ β
2
0
d
1
)]
The roots of p(t) are computed and X = (I +2tA)
−1
(Y −tB) is computed for each
root t. The minimum squared distance is selected from the set of values X(t) − Y
2
for all roots t.
Numerical concerns are warranted with this algorithm. If the curve is a parabola,
then d
0
d
1
= 0, in which case p
4
= 0. If d
0
d
1
is nearly zero, then the curve is not a
parabola, but p
4
is nearly zero itself. A numerical polynomial root finder must be
robust enough to handle such a situation. If the curve is a circle and Y is the center of
the circle, then all points on the circle attain minimum distance to Y . The coefficients
of the polynomial are identically zero. If the curve is an ellipse that is nearly circular
in shape, then the leading coefficient of the polynomial could be sufficiently close to
zero to cause problems with a root finder.
6.5 Point to Polynomial Curve
We consider the case of a curve X(t) =
n
i=0
A
i
t
i
,where
A
n
=
0. Let Y be the test
point. Just as in the case of quadratic curves, the closest point X(t) must satisfy the
condition that Y −X(t) is normal to the curve, but only when t is an interior point
of the domain of the function. It is possible that the closest point is an end point of
the curve; distance to end points can be computed separately. Equivalently for the
closest interior point, Y − X(t) must be perpendicular to the curve tangent
X
(t).
Figure 6.15 illustrates this. The interior point condition and end point testing follow
from a direct application of calculus to minimizing the squared-distance function
F(t) =X(t) − Y
2
for t ∈ I,whereI is the domain interval for the curve. The
global minimum of F must occur either where F
(t) = 0 or at an end point of I
(if any exist). Since F(t)= (X(t) − Y)· (X(t) − Y), half the derivative is F
(t)/2 =
(X(t) − Y) ·
X
(t). The right-hand side is the dot product of two vector-valued
polynomials. The result is a scalar-valued polynomial of degree 2n − 1. The problem
of computing the minimum distance is reduced to finding the roots of a polynomial.
Specifically, define
B
0
=
A
0
− Y and
B
i
=
A
i
for i ≥ 1. The derivative of the
curve function is
X
(t) =
n−1
j=0
(j +1)
B
j+1
t
j
. Define
C
i,j
=(j +1)
B
i
·
B
j+1
for the
appropriate values of i and j ; then
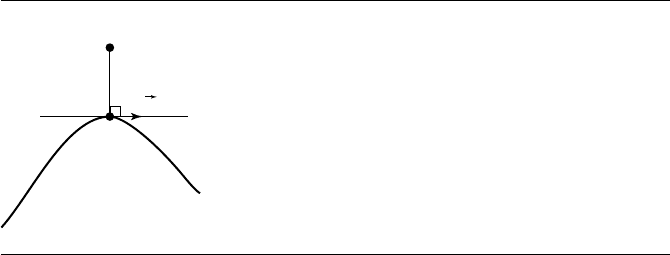
220 Chapter 6 Distance in 2D
X´
X
Y
Figure 6.15 Closest point on a polynomial curve to a given point.
F
(t)/2 = (X(t) − Y)·
X
(t)
=
n
i=0
n−1
j=0
(j + 1)
B
i
·
B
j+1
t
i+j
=
2n−1
k=0
k
m=max{0,k−n}
C
k−m,m
t
k
=
2n−1
k=0
D
k
t
k
(6.8)
where the last equality defines the D
k
terms. The candidates for minimum dis-
tance are those t such that F
(t) = 0, or equivalently, those t that are solutions to
2n−1
k=0
D
k
t
k
= 0.
For large degrees, numerical polynomial root finders can be ill conditioned. An
alternative to solving the problem uses a numerical minimizer for F(t). The mini-
mizer can use derivative information since
X
(t) is readily computed (for example,
Brent’s method, discussed in Section A.6) or can use just X(t) itself (for example,
Powell’s direction set method, also discussed in Section A.6).
Another alternative is to subdivide the curve to approximate it by a polyline
(see Section A.8), then compute the distance from Y to the polyline as an attempt
to approximate the distance or to localize the search for the closest point. In the
latter case, the numerical minimizer may be applied on the curve parameter intervals
corresponding to the line segments that yielded the smallest distances among all line
segments.
After subdivision, the squared distances are calculated between Y and the polyline
of the subdivision. On a final subinterval [t
0
, t
1
] in the subdivision, the derivative of
the squared-distance polynomial P(t) in Equation 6.8 can be tested for roots on

6.6 Linear Components 221
[t
0
, t
1
] (see the subsection in Section A.5 on Sturm sequences for polynomials). If
there are no roots, then P(t) is monotonic on the interval, and the minimum and
maximum distances occur at t
0
and t
1
. If the subinterval is an interior one, then the
minimum distance is not attained on the subinterval. If t
0
or t
1
are end points of
the original parameter interval, then the squared distances at those points must be
compared to any interior local minima that are calculated. If P
(t) hasonerooton
the subinterval, then a robust method such as bisection can be applied to locate the
root. If P
(t) has multiple roots on the subinterval, further subdivision should be
applied to obtain only intervals that have at most one root.
6.6 Linear Components
This section covers the distance algorithms for the six combinations of lines, rays, or
line segments: line-line, line-ray, line-segment, ray-ray, ray-segment, and segment-
segment.
6.6.1 Line to Line
Let the lines be represented by normal forms n
i
· X = c
i
for i = 0, 1. If the two
lines intersect, the distance is zero. Otherwise the lines are parallel, and the distance
between the lines is positive if the lines are disjoint or zero if the lines are the same.
Figure 6.16 illustrates the possibilities. In the case of parallel lines, the distance is
attained at a point P
0
on the first line and a point P
1
= P
0
+ t n
0
on the second
line. The distance itself is t n
0
.Thevalueoft is determined by c
1
=n
1
· P
1
=
n
1
· P
0
+ t n
1
·n
0
, in which case t = (c
1
−n
1
· P
0
)/(n
1
·n
0
). A point on the first line
is P
0
= c
0
n
0
/n
0
2
. Replacing this in the equation for t, substituting that into t n
0
,
and rearranging some terms leads to the distance formula
Distance
L
0
, L
1
=
0, n
0
·n
⊥
1
= 0
|(n
0
·n
0
)c
1
−(n
0
·n
1
)c
0
|
n
0
|n
0
·n
1
|
, n
0
·n
⊥
1
= 0
(6.9)
If n
0
=n
1
, the second portion of the distance formula reduces to |c
1
− σc
0
|/
n
0
,whereσ = Sign(n
0
·n
1
). The division is avoided if additionally n
0
=1.
The equivalent formula for the parametric representations P
i
+ t
i
d
i
, i =0, 1, is
Distance
L
0
, L
1
=
0,
d
0
·
d
⊥
1
= 0
|
d
⊥
0
·
|
d
0
,
d
0
·
d
⊥
1
= 0
(6.10)
where
=P
1
−P
0
. The second portion of the formula is the length of the projection
of
onto a normal line that is perpendicular to the two given lines.

222 Chapter 6 Distance in 2D
(a) (b)
Figure 6.16 Various line-line configurations: (a) zero distance; (b) positive distance.
6.6.2 Line to Ray
The distance calculations are similar to the case for line versus line. The only differ-
ence is that if the line L and ray R are not parallel, the ray might not intersect the
line. Figure 6.17 shows the possibilities. Let the normal representation for the line be
n
0
·X = c
0
. Let the ray be represented parametrically as P
1
+t
d
1
for t ≥0. If P
1
is on
the side of the line to which n
0
points, then the line and ray intersect if the ray points
toward the line, that is, if n
0
·
d
1
< 0. In this case the distance between the line and the
ray is zero. Otherwise, the ray points away from the line and the distance is attained at
P
1
on the ray and its projection onto the line; call this point P
0
. Similarly, if P
1
is on
the opposite side of the line to which n
0
points, then the line and ray intersect if the
ray points toward the line, that is, if n
0
·
d
1
> 0. Otherwise, the ray points away from
the line, and the distance is attained at P
1
and its projection onto the line, P
0
.Inthe
nonintersection case, if
= P
1
− P
0
, then the distance between the line and the ray
is |n
0
·
|/n
0
=|n
0
· P
1
− c
0
|/n
0
. Thus, it is not necessary to actually compute
P
0
when computing the distance. The distance is summarized by
Distance
L, R
=
0, (n
0
·
d
1
)(n
0
· P
1
− c
0
)<0
|n
0
·P
1
−c
0
|
n
0
, (n
0
·
d
1
)(n
0
· P
1
− c
0
) ≥ 0
(6.11)
The equivalent formula for the parametric line P
0
+ t
0
d
0
, t
0
∈ R, and the para-
metric ray P
1
+ t
1
d
1
, t
1
≥ 0, is
Distance
L, R
=
0, (
d
⊥
0
·
d
1
)(
d
⊥
0
·
) < 0
|
d
⊥
0
·
|
d
0
, (
d
⊥
0
·
d
1
)(
d
⊥
0
·
) ≥ 0
(6.12)
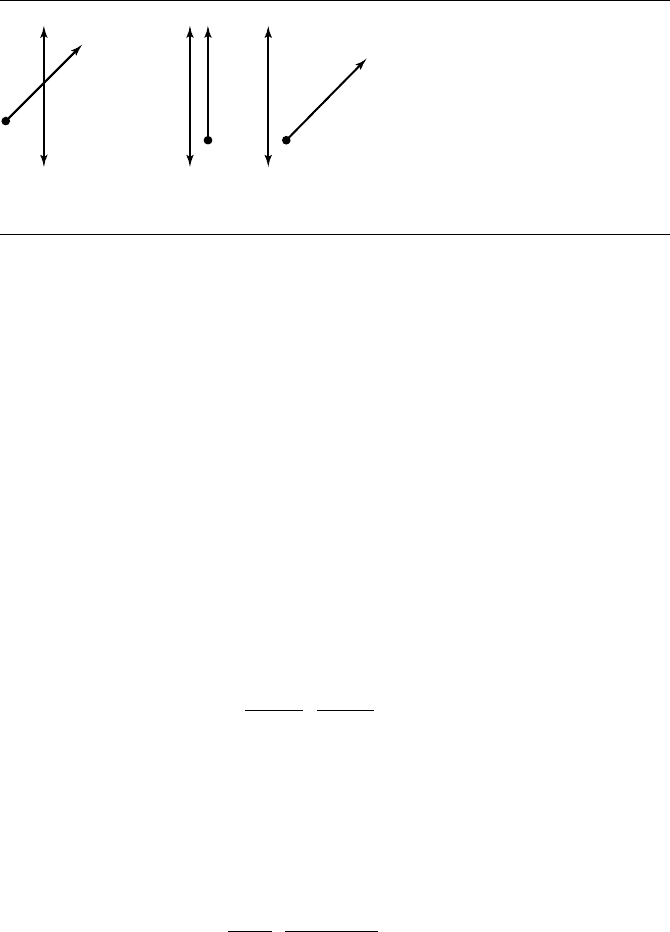
6.6 Linear Components 223
(a) (b)
Figure 6.17 Various line-ray configurations: (a) zero distance; (b) positive distance.
where
=P
1
−P
0
and (x, y)
⊥
=(y, −x). The second portion of the formula is the
length of the projection of
onto a normal line that is perpendicular to the two given
lines.
6.6.3 Line to Segment
Given a line L represented by n · X =c and a line segment S with end points Q
0
and
Q
1
, either they intersect, in which case the distance between them is zero, or they do
not intersect, in which case the distance between them is attained by the closer of the
two line segment end points. Figure 6.18 shows the possibilities. The distance is
Distance
L, S
=
0, (n · Q
0
− c)(n · Q
1
− c) < 0
min
|n·Q
0
−c|
n
,
|n·Q
1
−c|
n
, (n · Q
0
− c)(n · Q
1
− c) ≥0
(6.13)
The equivalent formula for the parametric line P
0
+ t
0
d
0
, t
0
∈ R, and the para-
metric segment P
1
+ t
1
d
1
, t
1
∈ [0, T
1
], i s
Distance
L, S
=
0, (
d
⊥
0
·
)(
d
⊥
0
· (
+ T
1
d
1
)) < 0
min
|
d
⊥
0
·
|
d
0
,
|
d
⊥
0
·(
+T
1
d
1
)|
d
0
, (
d
⊥
0
·
)(
d
⊥
0
· (
+ T
1
d
1
)) ≥ 0
(6.14)
where
= P
1
− P
0
.
