Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

234 Chapter 6 Distance in 2D

become known as the GJK algorithm, where the acronym is just the initial letters of

the last names of the authors of the paper. The algorithm was later extended to handle

convex objects in general (Gilbert and Foo 1990). An enhancement of the algorithm

was also developed that computes penetration distances when the polyhedra are

intersecting (Cameron 1997).

6.10.1 Set Operations

The Minkowski sum of two sets A and B is deﬁned as the set of all sums of vector

pairs, one from each set. Formally, the set is A + B ={X +Y : X ∈ A, Y ∈B}.The

negation ofasetB is −B ={−X : X ∈ B}.TheMinkowski difference of the sets is

A − B ={X −Y : X ∈ A, Y ∈ B}. Observe that A − B = A + (−B). If the sets A

and B are both convex, then A + B, −B, and A − B are all convex sets. If A is a

convex polygon with n vertices and B is a convex polygon with m vertices, in the

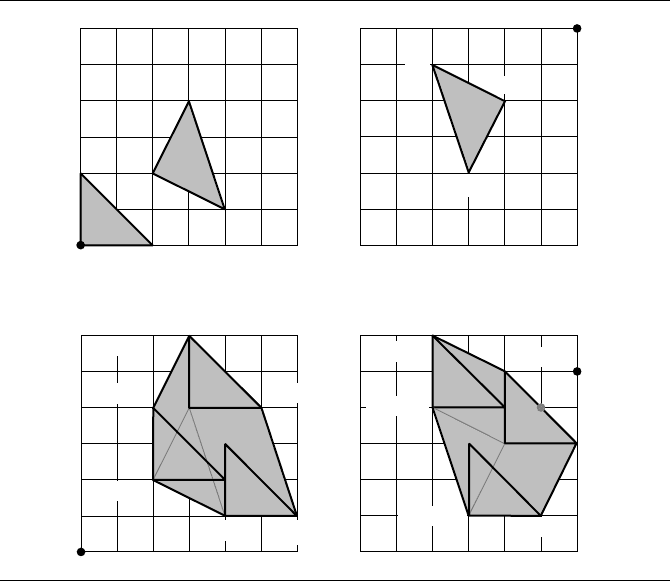
worst case the sum A + B has n + m vertices. Figure 6.24 illustrates where A is

the triangle U

, U

=(0, 0), (2, 0), (0, 2) and B is the triangle V

, V

=

(2, 2), (4, 1), (3, 4). The origin (0, 0) is marked as a black dot.

Figure 6.24(a) shows the original triangles. Figure 6.24(b) shows −B. Figure

6.24(c) shows A + B. To provide some geometric intuition on the sum, the ﬁgure

shows three triangles, with black edges corresponding to triangle A translated by each

of the three vertices of triangle B. Triangle B itself is shown with gray edges. Imagine

painting the hexagon interior by the translated triangle A where you move U

+ V

within triangle B. The same geometric intuition is illustrated in the drawing of A −B

(Figure 6.24(d)).

The distance between any two sets A and B is formally

Distance(A, B) = min{X − Y  : X ∈ A, Y ∈ B}=min{Z: Z ∈A − B}

The latter equation shows that the Minkowski difference can play an important role

in distance calculations. The minimum distance is attained by a point in A − B that

is closest to the origin. Figure 6.24(d) illustrates this for two triangles. The closest

point to the origin is the dark gray dot at the point (−1, −1) ∈ A − B. That point is

generated by (1, 1) ∈ A and (2, 2) ∈ B, so the distance between A and B is

√

2 and is

attained by the aforementioned points.

The heart of the distance calculation is how to efﬁciently search A − B for the

closest point to the origin. A straightforward algorithm is to compute A −B directly,

then iterate over the edges and compute the distance from each edge to the origin. The

minimum such distance is the distance between A and B. However, this approach is

not efﬁcient in that it can take signiﬁcant time to compute A − B as the convex hull

of the set of points U − V ,whereU isavertexofA and V isavertexofB.Moreover,

an exhaustive search of the edges will process edges that are not even visible to the

origin. The approach is O(nm) where A has n vertices and B has m vertices since the

convex hull can have nm vertices. The GJK algorithm is an iterative method designed

6.10 GJK Algorithm 235

– V

A – B

–V

+ V

A + B

(a) (b)

–B

+ V

Figure 6.24 (a) Triangles A and B; (b) set −B; (c) set A +B; (d) set A −B, where the gray point

is the closest point in A − B to the origin. The black dots are the origin (0, 0).

to avoid the direct convex hull calculation and to localize the search to edges near the

origin.

6.10.2 Overview of the Algorithm

The discussion here is for the general n-dimensional problem for convex objects A

and B.LetC = A − B,whereA and B are convex sets. As noted earlier, C itself is a

convex set. If 0 ∈ C, then the original sets intersect and the distance between them is

zero. Otherwise, let Z ∈C be the closest point to the origin. It is geometrically clear

that only one such point exists and must lie on the boundary of C. However, there

can be many X ∈ A and Y ∈ B such that X −Y =Z. For example, this happens for

two disjoint convex polygons in 2D whose closest features are a pair of parallel edges,

onefromeachpolygon.

236 Chapter 6 Distance in 2D

The GJK algorithm is effectively a descent method that constructs a sequence of

points on the boundary of C, each point having smaller distance to the origin than

the previous point in the sequence. In fact, the algorithm generates a sequence of

simplices with vertices in C (triangles in 2D, tetrahedra in 3D), each simplex having

smaller distance to the origin than the previous simplex. Let S

denote the simplex

vertices at the kth step, and let

denote the simplex itself. The point V

∈

selected to be the closest point in

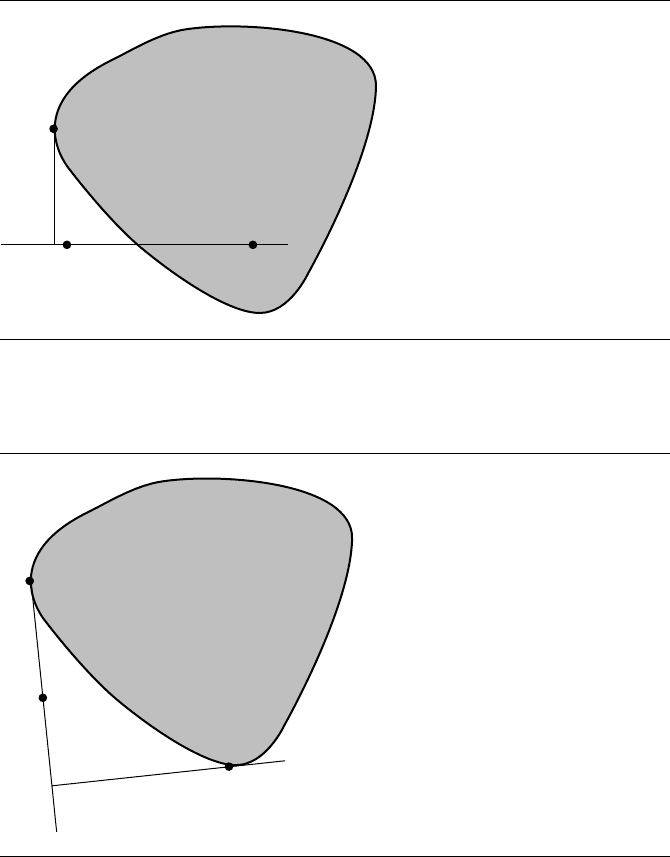
to the origin. Initially, S

=∅(the empty set)

and V

is an arbitrary point in C. The set C is projected onto the line through 0 with

direction V

, the resulting projection being a closed and bounded interval on the line.

The interval end point that is farthest left on the projection line is generated by a point

∈C. The next set of simplex vertices is S

={W

}. Figure 6.25 illustrates this step.

Since S

is a singleton point set,

= S

and V

= W

is the closest point in

to the origin. The set C is now projected onto the line containing 0 with direction

. The interval end point that is farthest left on the projection line is generated by a

point W

∈C. The next set of simplex vertices is S

={W

, W

}. Figure 6.26 illustrates

this step.

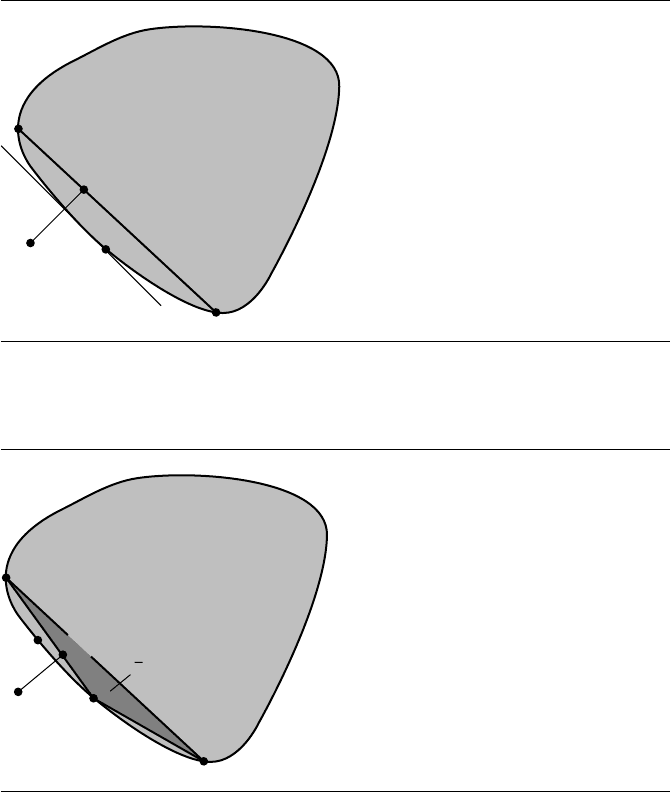
The set

is the line segment W

, W

. The closest point in

to the origin is

an edge-interior point V

. The set C is projected onto the line containing 0 with

direction V

. The interval end point that is farthest left on the projection line is

generatedbyapointW

∈ C. The next set of simplex vertices is S

={W

, W

Figure 6.27 illustrates this step.

The set

is the triangle W

, W

. The closest point in

to the origin is

a point V

on the edge W

, W

. The next simplex vertex that is generated is W

The next set of simplex vertices is S

=W

, W

. The old simplex vertex W

discarded. Figure 6.28 illustrates this step. The simplex

is shown in dark gray.

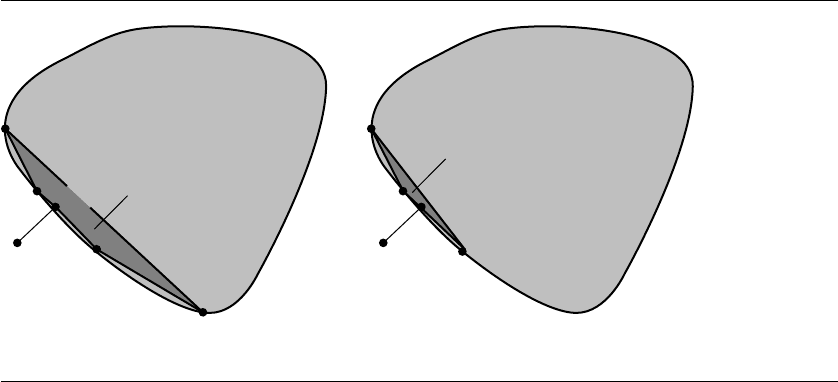
Generally, V

k+1

is chosen to be the closest point to the origin in the convex hull

of S

∪{W

}. The next set of simplex vertices S

k+1

is chosen to be set M ⊆ S

∪{W

}

with the fewest number of elements such that V

k+1

is in the convex hull of M. Such

asetM must exist and is unique. Figure 6.29(a) shows the convex hull of S

∪{W

a quadrilateral. The next iterate V

is shown on that hull. Figure 6.29(b) shows the

simplex

that was generated by M ={W

, W

We state without proof that the sequence of iterates is monotonically decreasing

in length, V

k+1

≤V

. In fact, equality can only occur if V

=Z, the closest point.

For convex faceted objects, the closest point is reached in a ﬁnite number of steps. For

general convex objects, the sequence can be inﬁnite, but must converge to Z.Ifthe

GJK algorithm is implemented for such objects, some type of termination criterion

must be used. Numerical issues also arise when the algorithm is implemented in a

ﬂoating-point number system. A discussion of the pitfalls is given by van den Bergen

(1997, 1999, 2001a), and the ideas are implemented in a 3D collision detection

system called SOLID (Software Library for Interference Detection) (van den Bergen

2001b). The main concern is that the simplices eventually become ﬂat in one or more

dimensions.

6.10 GJK Algorithm 237

Figure 6.25 The ﬁrst iteration in the GJK algorithm.

Figure 6.26

The second iteration in the GJK algorithm.

238 Chapter 6 Distance in 2D

Figure 6.27 The third iteration in the GJK algorithm.

Figure 6.28 The fourth iteration in the GJK algorithm.

6.10.3 Alternatives to GJK

The GJK algorithm is by no means the only algorithm for computing distance be-

tween convex polygons or convex polyhedra, but good, robust implementations are

publicly available (van den Bergen 2001b). The distance between two nonintersecting

convex polygons can be computed using the method of rotating calipers (Pirzadeh

1999). This powerful method is useful for solving many other types of problems in

6.10 GJK Algorithm 239

hull (S

})

⊃

(a) (b)

Figure 6.29 (a) Construction of V

k+1

in the convex hull of S

∪{W

}. (b) The new simplex

k+1

generated from M ={W

, W

computational geometry. Assuming both polyhedra have O(n) vertices, an O(n

) al-

gorithm, both in space and in time, for computing the distance is given by Cameron

and Culley (1986). An asymptotically better algorithm is given by Dobkin and Kirk-

patrick (1990) and is O(n) in space and O(log

n) in time. However, no imple-

mentation appears to be publicly available. The method is based on constructing a

hierarchical representation of a polyhedron that is useful for solving other queries,

for example, in rapid determination of an extreme point of a polyhedron for a speci-

ﬁed direction. In more recent times, the Lin-Canny algorithm (Lin and Canny 1991)

is O(n) in space, empirically O(n) in time, but maintains the closest pair of features

to exploit frame coherence. After computing the distance in one frame, the polyhedra

move slightly, and the distance must be recalculated in the next frame. The incre-

mental update is O(1) in time. Implementations based on this method are I-Collide

(Cohen et al. 1995) and V-Clip (Mirtich 1997).

Chapter

7Intersection in 2D

This chapter contains information on computing the intersection of geometric prim-

itives in 2D. The simplest object combinations to analyze are those for which one of

the objects is a linear component (line, ray, segment). These combinations are cov-

ered in the ﬁrst four sections. Section 7.5 covers the intersection of a pair of quadratic

curves; Section 7.6 covers the problem of intersection of a pair of polynomial curves.

The last section is about the method of separating axes, a very powerful technique for

dealing with intersections of convex objects.

7.1 Linear Components

Recall from Chapter 5 the deﬁnitions for lines, rays, and segments. A line in 2D is

parameterized as P + t



d,where



d is a nonzero vector and where t ∈ R.Aray is

parameterized the same way except that t ∈ [0, ∞). The point P is the origin of the

ray. A segment is also parameterized the same way except that t ∈[0, 1]. The points P

and P +



d are the end points of the segment. A linear component is the general term

for a line, a ray, or a segment.

Given two lines P

+ s



and P

+ t



for s, t ∈ R, they are either intersect-

ing, nonintersecting and parallel, or the same line. To help determine which of

these cases occurs, deﬁne for two input 2D vectors the scalar-valued operation

Kross((x

, y

), (x

, y

)) = x

− x

. The operation is related to the cross product

in 3D given by (x

, y

,0) ×(x

, y

,0) =(0, 0, Kross((x

, y

), (x

, y

))). The operation

has the property that Kross(u, v) =−Kross(v, u).

A point of intersection, if any, can be found by solving the two equations in

two unknowns implied by setting P

+ s



= P

+ t



. Rearranging terms yields



− t



= P

− P

. Setting



 = P

− P

and applying the Kross operation yields

241

242 Chapter 7 Intersection in 2D

Kross(



)s= Kross(



,



) and Kross(



)t = Kross(



,



). If Kross(



)

= 0, then the lines intersect in a single point determined by s = Kross(



,



Kross(



) or t = Kross(



,



)/Kross(



).IfKross(



) = 0, then the lines

are either nonintersecting and parallel or the same line. If the Kross operation of the

direction vectors is zero, then the previous equations in s and t reduce to a single

equation Kross(



,



) = 0 since



is a scalar multiple of



. The lines are the same if

this equation is true; otherwise, the lines are nonintersecting and parallel.

If using ﬂoating-point arithmetic, distinguishing the nonparallel from the parallel

case can be tricky when Kross(



) is nearly zero. Using the relationship of Kross

to the 3D cross product, a standard identity for the cross product in terms of Kross

is Kross(



)=







| sin θ |,whereθ is the angle between



and



.For

the right-hand side of the last equation to be nearly zero, one or more of its three

terms must be nearly zero. A test for parallelism using an absolute error comparison

Kross(



)≤ε for some small tolerance ε>0 may not be suitable for some

applications. For example, two perpendicular direction vectors that have very small

length can cause the test to report that the lines are parallel when in fact they are

perpendicular. If possible, the application should require that the line directions be

unit-length vectors. The absolute error test then becomes a test on the sine of the

angle between the directions: Kross(



)=|sin θ|≤ε. For small enough angles,

the test is effectively a threshold on the angle itself since sin θ

θ for small angles. If

the application cannot require that the line directions be unit length, then the test for

parallelism should be based on relative error:

Kross(



)











=|sin θ|≤ε

The square root calculations for the two lengths and the division can be avoided by

using instead the equivalent inequality

Kross(



)

≤ ε











If the two linear components are a line (s ∈ R)andaray(t ≥ 0), the point of

intersection, if it exists, is determined by solving for s and t as shown previously.

However, it must be veriﬁed that t ≥ 0. If t<0, the ﬁrst line intersects the line

containing the ray, but not at a ray point. Computing the solution t as speciﬁed earlier

involves a division. An implementation can avoid the cost of the division when testing

t ≥ 0 by observing that t = Kross(



,



)Kross(



)/(Kross(



))

and using the

equivalent test Kross(



,



)Kross(



) ≥ 0. If in fact the equivalent test shows that

t ≥ 0 and if the application needs to know the corresponding point of intersection,

only then should t be directly computed, thus deferring a division until it is needed.

Similar tests on s and t may be applied when either linear component is a ray or a

segment.

7.1 Linear Components 243

Finally, if the two linear components are on the same line, the linear com-

ponents intersect in a t-interval, possibly empty, bounded, semi-inﬁnite, or inﬁ-

nite. Computing the interval of intersection is somewhat tedious, but not com-

plicated. As an example, consider the case when both linear components are line

segments, so s ∈ [0, 1] and t ∈ [0, 1]. We need to compute the s-interval of the sec-

ond line segment that corresponds to the t-interval [0, 1]. The ﬁrst end point is

represented as P

= P

+ s



; the second is represented as P



= P

+ s



 = P

− P

, then s



/





and s

= s



/





.Thes-interval

is [s

min

, s

max

] = [min(s

, s

), max(s

, s

)]. The parameter interval of intersection is

[0, 1] ∩[s

min

, s

max

], possibly the empty set. The 2D points of intersection for the line

segment of intersection can be computed from the interval of intersection by using

the interval end points in the representation P

+ s



The pseudocode for the intersection of two lines is presented below. The return

value of the function is 0 if there is no intersection, 1 if there is a unique intersection,

and 2 if the two lines are the same line. The returned point

I is valid only when the

function returns 1.

int FindIntersection(Point P0, Point D0, Point P1, Point D1, Point& I)

{

// Use a relative error test to test for parallelism. This effectively

// is a threshold on the angle between D0 and D1. The threshold

// parameter ’sqrEpsilon’ can be defined in this function or be

// available globally.

PointE=P1-P0;

float kross = D0.x * D1.y - D0.y * D1.x;

float sqrKross = kross * kross;

float sqrLen0 = D0.x * D0.x + D0.y * D0.y;

float sqrLen1 = D1.x * D1.x + D1.y * D1.y;

if (sqrKross > sqrEpsilon * sqrLen0 * sqrLen1) {

// lines are not parallel

float s = (E.x * D1.y - E.y *D1.x) / kross;

I=P0+s*D0;

return 1;

}

// lines are parallel

float sqrLenE = E.x * E.x + E.y * E.y;

kross = E.x * D0.y - E.y * D0.x;

sqrKross = kross * kross;

if (sqrKross > sqrEpsilon * sqrLen0 * sqrLenE) {

// lines are different

return 0;

}