Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

394 Chapter 10 Distance in 3D
P
v
C
h
w
h
u
h
v
u
w
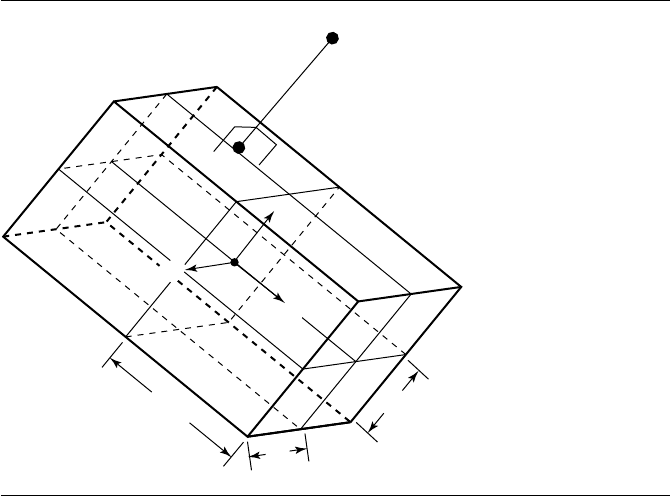
Figure 10.21 Distance from a point to an oriented bounding box.
10.4.2 Point to Oriented Bounding Box
In this section we address the problem of computing the distance from a point to
an oriented bounding box (OBB). An OBB is defined as a centerpoint C; three unit
vectors ˆu, ˆv, and ˆw forming a right-handed orthornormal basis; and three scalars
h
u
, h
v
, and h
w
representing half the dimension in each of the u, v, and w directions.
This can be seen in Figure 10.21.
We could, of course, consider that an OBB consists of six rectangles, and simply
compute the distance from the point to each rectangle, and take the minimum;
however, this is inefficient.
The OBB’s centerpoint C and ˆu, ˆv, and ˆw define a frame. Observe that, relative
to that frame, the OBB is an axis-aligned box centered at the origin, whose sides lie
in one of the XY, XZ,orYZ planes. If we compute the position of a point P in this
frame, then we can exploit this axis-aligned, origin-centered nature of the OBB and
compute the closest point, and the distance to it, quite trivially.
Given the OBB’s center C and ˆu, ˆv, and ˆw, a point P ’s coordinates in that frame
can be computed as
P
=
[
(P − C) ·ˆu(P− C) ·ˆv(P− C) ·ˆw
]
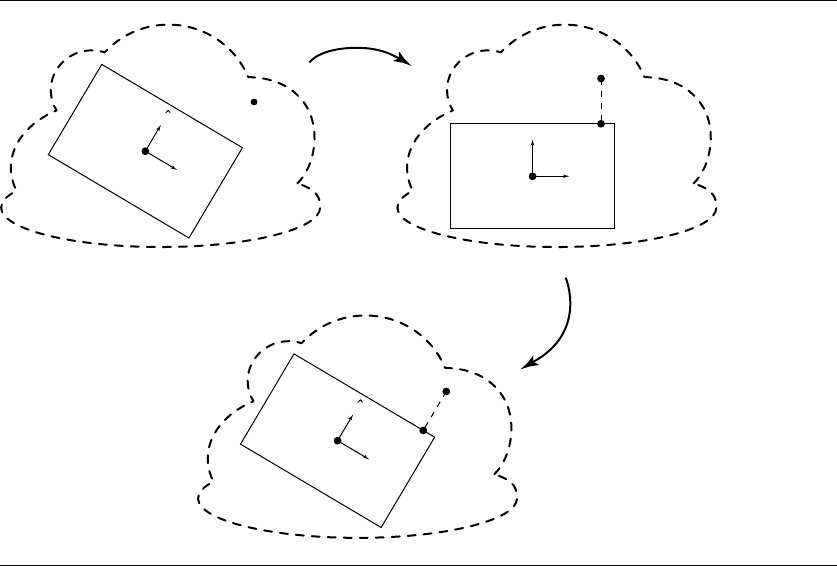
10.4 Point to Polyhedron 395
v
C
P
C
P'
Q'
C
P
Q
T
T
–1
x
y
û
v
û
Figure 10.22 Computing the distance between a point and an OBB.
That is, we simply project the vector between the P and C onto each of the OBB’s
basis vectors. Note that this is functionally equivalent to creating a transform T from
global space into the local space of the OBB with matrix
T =
ˆu
T
ˆv
T
ˆw
T
0
T
−C 1
and multiplying by P , but is more efficient.
We can then simply project P
onto the box—this yields a point Q
closest to
P
—and trivially find the distance between them, which is also the distance between
the original point P and the box. If we want the coordinates of the closest point in
global space, we simply transform Q
by the T
−1
, yielding the point Q closest to P .
An example of this, shown in 2D for ease of illustration, appears in Figure 10.22.
The pseudocode is below (note we compute the distance squared and return the
nearest point Q only if asked):
396 Chapter 10 Distance in 3D
float PointOBBDistanceSquared(Point p, OBB box, boolean computePoint,
Point& q)
{
// Transform p into box’s coordinate frame
Vector offset=p-box.center();
Point pPrime(Dot(offset, box.u), Dot(offset, box.v), Dot(offset, box.w));
// Project pPrime onto box
float distanceSquared = 0;
float d;
if (pPrime.x < -box.uHalf) {
d = pPrime.x + box.uHalf;
distanceSquared +=d*d;
qPrime.x = -box.uHalf;
} else if (pPrime.x > box.uHalf) {
d = pPrime.x - box.uHalf;
distanceSquared +=d*d;
qPrime.x = box.uHalf;
} else {
qPrime.x = pPrime.x;
}
if (pPrime.y < -box.vHalf ) {
d = pPrime.y + box.v;
distanceSquared +=d*d;
qPrime.y = -box.vHalf;
} else if (pPrime.y > box.vHalf) {
d = pPrime.y - box.vHalf;
distanceSquared +=d*d;
qPrime.y = box.vHalf;
} else {
qPrime.y = pPrime.y;
}
if (pPrime.z < -box.wHalf) {
d = pPrime.z + box.wHalf;
distanceSquared +=d*d;
qPrime.z = -box.wHalf;
} else if (pPrime.z > box.wHalf) {
d = pPrime.z - box.wHalf;
distanceSquared +=d*d;
qPrime.z = box.wHalf;
} else {
10.4 Point to Polyhedron 397
qPrime.z = pPrime.z;
}
// If requested, compute the nearest point in global space (T^{-1})
if (computePoint) {
q.x = qPrime.x * box.u.x + qPrime.y * box.v.x + qPrime.z * box.w.x;
q.y = qPrime.x * box.u.y + qPrime.y * box.v.y + qPrime.z * box.w.y;
q.x = qPrime.x * box.u.z + qPrime.y * box.v.z + qPrime.z * box.w.z;
q += box.center;
}
return distanceSquared;
}
10.4.3 Point to Orthogonal Frustum
The material in this section is motivated in two dimensions in Section 6.3.3. The
algorithm for computing the distance from a point to an orthogonal frustum is based
on determining the Voronoi regions for the faces, edges, and vertices of the frustum.
Given a set of objects, the Voronoi region for a single object is the set of all points that
are closer to that object than to any other object. The Voronoi region containing the
point is computed. The nearest point on the frustum in that region is also computed.
From this the distance can be calculated.
The orthogonal view frustum has origin E. Its coordinate axes are determined by
left vector
ˆ
l, up-vector ˆu, and direction vector
ˆ
d. The vectors in that order form a
right-handed orthonormal system. The extent of the frustum in the
ˆ
d direction is
[n, f ], w h er e 0 <n<f. The four corners of the frustum in the near plane are E ±
6
ˆ
l ±µ ˆu +n
ˆ
d. The four corners of the frustum in the far plane are E +(f/n)(±6
ˆ
l ±
µ ˆu + n
ˆ
d). The frustum axis is the ray with origin E and direction
ˆ
d. The frustum is
orthogonal in the sense that its axis is perpendicular to the near and far faces.
Let P be the point whose distance to the frustum is required. The point can be
written in the frustum coordinate system as
P = E +x
0
ˆ
l +x
1
ˆu + x
2
ˆ
d
so x
0
=
ˆ
l ·(P −E), x
1
=ˆu ·(P −E), and x
2
=
ˆ
d ·(P −E). It is sufficient to demon-
strate the construction for x
0
≥ 0 and x
1
≥ 0. The idea is the same as in the 2D case:
reflect the x
0
and x
1
components, find the closest point, then reflect its x
0
and x
1
components back to the original quadrant.
The naming conventions for the frustum components are N for near, F for far,
U for up, and L for left. The top face of the frustum is labeled the F -face. It has two
edges: the UF-edge that is in the direction of
ˆ
l and the LF -edge that is in the direction
398 Chapter 10 Distance in 3D
n
f
E
û
d
ˆ
l
ˆ
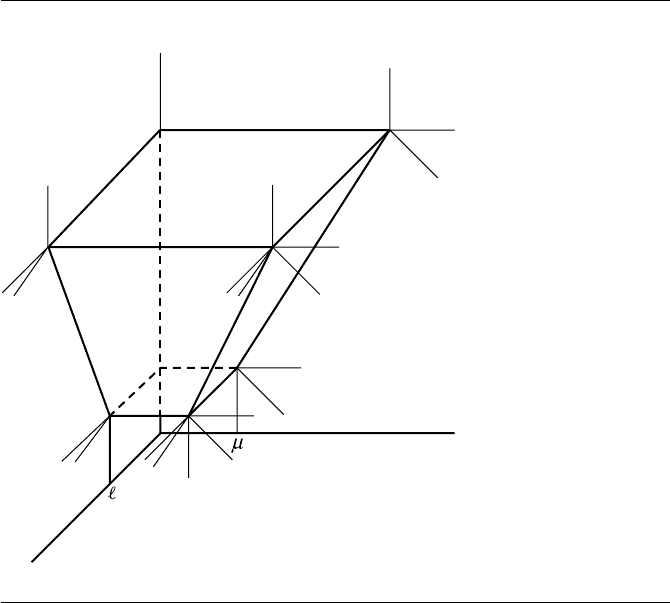
Figure 10.23 The portion of the frustum in the first octant.
of ˆu. It also has a vertex: the LUF -vertex at (f 6/n, fµ/n, f). The bottom face of the
frustum is labeled the N -face. It has two edges: the UN-edge that is in the direction
of
ˆ
l and the LN-edge that is in the direction of ˆu. It also has a vertex: the LUN -vertex
at (6, µ, n). The remaining two faces are the L-face whose normal is (n,0,−6) and
the U -face whose normal is (0, n, −µ). Finally there is the LU -edge that is shared
by the L-face and the U-face. Figure 10.23 illustrates the Voronoi region boundaries.
The thin black lines indicate the near and far planes that split some of the Voronoi
regions.
The pseudocode for determining the Voronoi region for (x
0
, x
1
, x
2
) is given
below.
if (x2 >= f) {
if(x0<=f*l/n){
if(x1<=f*u/n)
10.4 Point to Polyhedron 399
F-face is closest;
else
UF-edge is closest;
} else {
if(x1<=f*u/n)
LF-edge is closest;
else
LUF-vertex is closest;
}
} else if (x2 <= n) {
if (x0 <= l) {
if (x1 <= u)
N-face is closest;
else {
t=u*x1+n*x2;
if(t>=(f/n)*(u*u+n*n))
UF-edge is closest;
else if (t >=u*u+n*n)
U-face is closest;
else
UN-edge is closest;
}
} else {
if (x1 <= u) {
t=l*x0+n*x2;
if(t>=(f/n)*(l*l+n*n))
LF-edge is closest;
else if (t >=l*l+n*n)
L-face is closest;
else
LN-edge is closest;
} else {
r=l*x0+u*x1+n*x2;
s=u*r-(l*l+u*u+n*n)*x1;
if (s >= 0.0) {
t=l*x0+n*x2;
if(t>=(f/n)*(l*l+n*n))
LF-edge is closest;
else if (t >=l*l+n*n)
L-face is closest;
else
LN-edge is closest;
} else {
s=l*r-(l*l+u*u+n*n)*x0;
400 Chapter 10 Distance in 3D
if (s >= 0.0) {
t=u*x1+n*x2;
if(t>=(f/n)*(u*u+n*n))
UF-edge is closest;
else if (t >=u*u+n*n)
U-face is closest;
else
UN-edge is closest;
} else {
if(r>=(f/n)(l*l+u*u+n*n))
LUF-vertex is closest;
else if (r >=l*l+u*u+n*n)
LU-edge is closest;
else
LUN-vertex is closest;
}
}
}
}
} else {
s=n*x0-l*x2;
t=n*x1-u*x2;
if (s <= 0) {
if (t <= 0)
point inside frustum;
else {
t=u*x1+n*x2;
if(t>=(f/n)*(u*u+n*n))
UF-edge is closest;
else
U-face is closest;
}
} else {
if (t <= 0) {
t=l*x0+n*x2;
if(t>=(f/n)*(l*l+n*n))
LF-edge is closest;
else
L-face is closest;
} else {
r=l*x0+u*x1+n*x2;
s=u*r-(l*l+u*u+n*n)*x1;
if (s >= 0) {
t=l*x0+n*x2;
10.5 Point to Quadric Surface 401
if(t>=(f/n)*(l*l+n*n))
LF-edge is closest;
else
L-face is closest;
} else {
t=l*r-(l*l+u*u+n*n)*x0;
if (t >= 0) {
t=u*x1+n*x2;
if(t>=(f/n)*(u*u+n*n))
UF-edge is closest;
else
U-face is closest;
} else {
if(r>=l*l+u*u+n*n)
LUF-vertex is closest;
else
LU-edge is closest;
}
}
}
}
}
The closest point in each region is obtained by projection onto that component.
10.5 Point to Quadric Surface
In this section we address the problem of computing the distance from a point to
a quadric surface. As we shall see, the general case involves solving a sixth-degree
equation: all the roots must be computed, and their associated distances compared,
in order to find the actual minimum distance. We can exploit the geometry of specific
types of quadrics and obtain a somewhat less expensive algorithm; the example we
give is for an ellipsoid.
10.5.1 Point to General Quadric Surface
This section describes an algorithm for computing the distance from a point to a
quadric surface. The general quadratic equation is
Q(X) = X
T
AX + B
T
X + c = 0
402 Chapter 10 Distance in 3D
where A is a symmetric 3 × 3 matrix, not necessarily invertible (for example, in the
case of a cylinder or paraboloid), B isa3×1 vector, and c is a scalar. The parameter
is X,a3× 1 vector. Given the surface defined implicitly by Q(X) = 0 and a point Y ,
find the distance from Y to the surface and compute a closest point X.
Geometrically, the closest point X on the surface to Y must satisfy the condition
that Y − X is normal to the surface. Since the surface gradient ∇Q(X) is normal to
the surface, the algebraic condition for the closest point is
Y − X =t∇Q(X) = t(2AX + B)
for some scalar t. Therefore,
X = (I + 2tA)
−1
(Y − tB)
where I is the identity matrix. We could replace this equation for X into the general
quadratic equation to obtain a polynomial in t of at most sixth degree.
Instead of immediately replacing X in the quadratic equation, we can reduce the
problem to something simpler to code. Factor A using an eigendecomposition to ob-
tain A =RDR
T
,whereR is an orthonormal matrix whose columns are eigenvectors
of A and where D is a diagonal matrix whose diagonal entries are the eigenvalues of
A. Then
X = (I + 2tA)
−1
(Y − tB)
= (RR
T
+ 2tRDR
T
)
−1
(Y − tB)
= [R(I + 2tD)R
T
]
−1
(Y − tB)
= R(I + 2tD)
−1
R
T
(Y − tB)
= R(I + 2tD)
−1
(α − t
β)
where the last equation defines α and
β. Replacing in the quadratic equation and
simplifying yields
0 =(α − t
β)
T
(I +2tD)
−1
D(I +2tD)
−1
(α − t
β) +
β
T
(I +2tD)
−1
(α − t
β) + C
The inverse diagonal matrix is
(I +2tD)
−1
= Diag{1/(1 + 2td
0
),1/(1 + 2td
1
),1/(1 + 2td
2
)}
Multiplying through by ((1 +2td
0
)(1+2td
1
)(1+2td
2
))
2
leads to a polynomial equa-
tion of at most sixth degree.

10.5 Point to Quadric Surface 403
The roots of the polynomial are computed and X = (I + 2tA)
−1
(Y − tB) is
computed for each root t. The distances between X and Y are computed, and the
minimum distance is selected from that set.
10.5.2 Point to Ellipsoid
The previous section discussed a general solution to the problem of the distance from
a point to a quadric surface. The equation of the intersection can be as much as a
sixth-degree equation; solutions for such equations exist, but they can be relatively
expensive.
For a specific type of quadric surface, simplifications can be made by exploiting
the geometry of the object. We’ll look at the ellipsoid as an example. The equation of
an ellipsoid is
q(x) =
x
2
a
2
+
y
2
b
2
+
z
2
c
2
− 1 = 0 (10.7)
Let P be the point from which we wish to compute the distance. The closest point on
the ellipsoid can be viewed as being connected by a line that is normal to P ; that is,
P − x =∇q(x) (10.8)
where x is the point on the surface and ∇q(x) is the normal to the ellipsoid at x.
The normal to a point on the surface of the ellipsoid is
∇q(X) =(
∂q
∂x
,
∂q
∂y
,
∂q
∂z
)
= 2(
x
a
2
,
y
b
2
,
z
c
2
)
(10.9)
Substituting Equation 10.9 into Equation 10.8 and then substituting the results into
Equation 10.7 will give us the equation we need to solve to find the closest point:
a
2
(λ + b
2
)
2
(λ + c
2
)
2
P
2
x
+ b
2
(λ + a
2
)
2
(λ + c
2
)
2
P
2
y
+ c
2
(λ + a
2
)
2
(λ + b
2
)
2
P
2
z
− (λ + a
2
)
2
(λ + b
2
)
2
(λ + c
2
)
2
= 0
To see that this is a sixth-degree equation, consider eliminating λ and then using
two of the equations to solve for, say, x and y in terms of the constants and z. This
yields this unpleasant equation:
