Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

384 Chapter 10 Distance in 3D
If the projected point is in region 0, then that projected point is the closest to Q.
If it instead is in any one of regions 2, 4, 6, or 8, then the closest point is P
2
, P
3
, P
0
,or
P
1
, respectively. Finally, if it is in any one of regions 1, 3, 5, or 7, then the closest point
is the projection of that point onto edge P
1
P
2
, P
2
P
3
, P
3
P
0
,orP
0
P
1
, respectively.
The projection of Q onto the plane containing R is
Q
= Q + s e
0
+ t e
1
where
s = (Q − P)·e
0
(10.5)
t = (Q − P)·e
1
(10.6)
The pseudocode is
float PointRectangleDistanceSquared3D(Point q, Rectangle rectangle)
{
floatd=q-rectangle.p;
float s = Dot(rectangle.e0, d);
if(s>0){
float dot0 = Dot(rectangle.e0, rectangle.e0);
if (s < dot0) {
d=d-(s/dot0) * rectangle.e0;
} else {
d=d-rectangle.e0;
}
}
float t = Dot (rectangle.e1, d);
if(t>0){
float dot1 = Dot(rectangle.e1, rectangle.e1);
if (t < dot1) {
d=d-(t/dot1) * rectangle.e1;
} else {
d=d-rectangle.e1;
}
}
return Dot(d, d);
}
10.3 Point to Planar Component 385
P
V
0
V
1
V
2
V
3
V
4
n
V
5
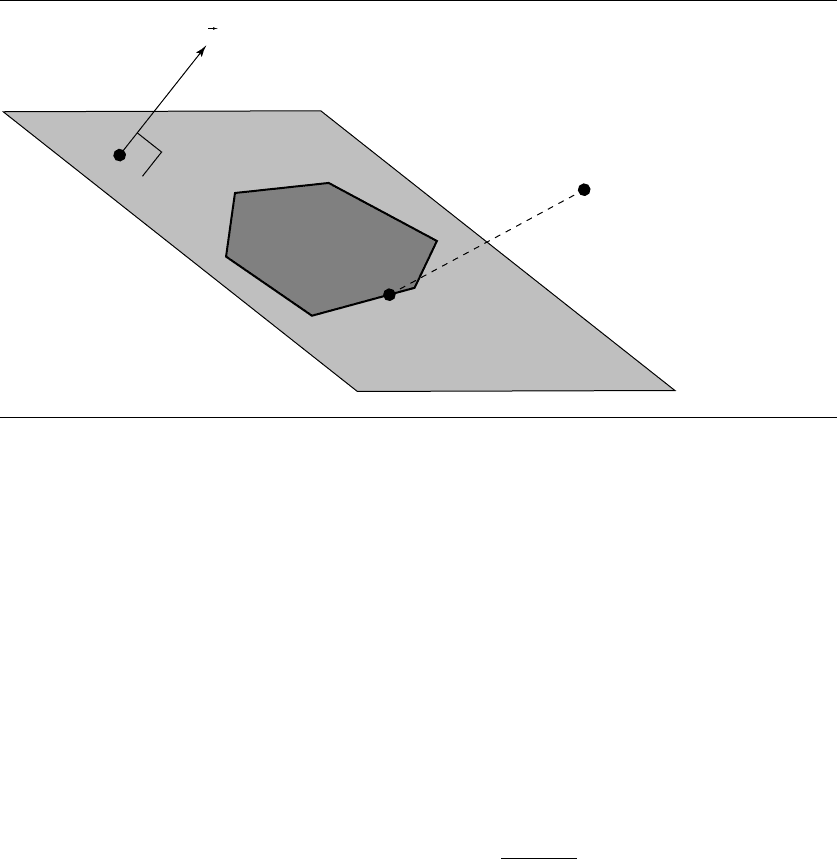
Figure 10.14 Distance from a point to a polygon.
10.3.4 Point to Polygon
In this section we address the problem of finding the distance from a point to a
polygon in 3D, as shown in Figure 10.14. A polygon is defined as a list of n vertices:
V
0
, V
1
, ..., V
n−1
. The plane in which these points lie can be computed by finding
three noncollinear and noncoincident points V
i
, V
j
, V
k
, i<j<k, by taking the
cross product (V
j
− V
i
) × (V
k
− V
i
) as the normal to the plane and any of V
i
,0≤
i ≤ n − 1, as a point on the plane. Given floating-point imprecision and the actual
computation involved in determining noncollinearity, it may be wise to instead use
Newell’s method (Tampieri 1992), described in Section A.7.4.
Let the plane of the polygon P be defined as ax +by +cz + d =. The projection
of the point P onto P is
P
= P −
P ·n + d
n ·n
n
Then if we project the V
i
and P
onto one of the XY , XZ,orYZ planes (typically,
we project along the axis that the points of the polygon differ least in), we can
compute Q
, the point on the (projected) polygon closest to P
, using the 2D point-
polygon distance algorithm found in Section 6.3.4. The point Q on the unprojected
polygon closest to P can be computed by plugging in the coordinates of Q
that
386 Chapter 10 Distance in 3D
P
V
0
V
1
V
2
V
3
V
4
V
5
Q'
P''
Q
n
P'
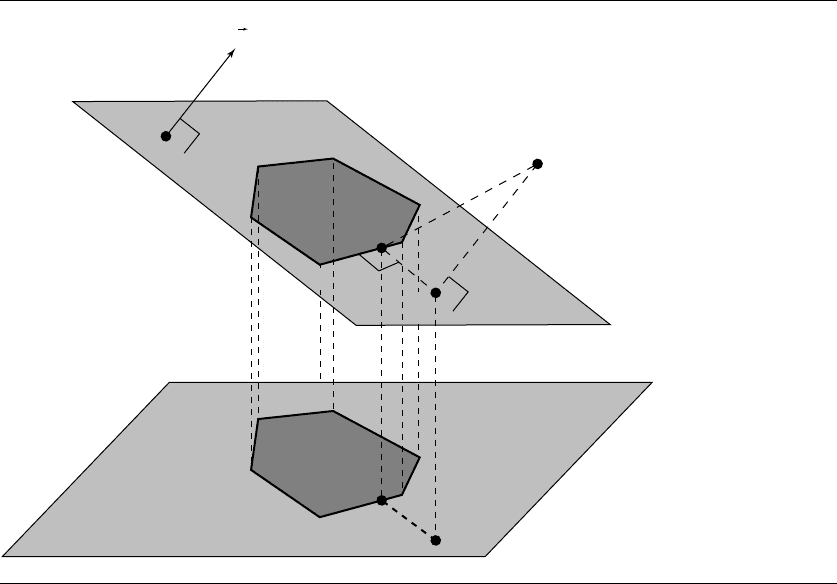
Figure 10.15 Solving the 3D point-polygon distance test by projecting to 2D.
did not correspond to the axis of projection into the plane equation of the polygon.
The distance between P and Q is then the distance from P to the polygon (see
Figure 10.15).
The pseudocode is
float PointPolygonDistanceSquared3D(Point p, Polygon poly)
{
// Get plane equation for polygon
float a, b, c, d;
PolygonPlaneEquation(poly, a, b, c, d);
Vectorn={a,b,c};
// Project point onto plane of polygon
Point pPrime;
10.3 Point to Planar Component 387
pPrime=p-((Dot(p, n) - d) / Dot(n, n)) * n;
// Determine plane to project polygon onto
if (MAX(n.x, MAX(n.y, n.z)) == n.x) {
projectionPlane = YZ_PLANE;
} else if (MAX(n.x, MAX(n.y, n.z)) == n.y) {
projectionPlane = XZ_PLANE;
} else {
projectionPlane = XY_PLANE;
}
// Project poly and pPrime onto plane
Point pPrimePrime = pPrime;
if (projectionPlane == YZ_PLANE) {
pPrimePrime.x = 0;
} else if (projectionPlane == XZ_PLANE) {
pPrimePrime.y = 0;
} else {
pPrimePrime.z = 0;
}
Polygon2D poly2D;
for (i = 0; i < poly.nVertices; i++) {
poly2D.vertices[i] = poly.vertices[i];
if (projectionPlane == YZ_PLANE) {
poly2D.vertices[i].x = 0;
} else if (projectionPlane == XZ_PLANE) {
poly2D.vertices[i].y = 0;
} else {
poly2D.vertices[i].z = 0;
}
}
// Find closest point in 2D
Point qPrime;
float dist2D;
dist2D = PointPolygonDistance2D(pPrimePrime, poly2D, qPrime);
// Compute q, the closest point on the 3D polygon’s plane
q = qPrime;
if (projectionPlane == YZ_PLANE) {
qPrime.x = (-b * qPrime.y-c*qPrime.z - d) / a;
} else if (projectionPlane == XZ_PLANE) {
388 Chapter 10 Distance in 3D
qPrime.y = (-a * qPrime.x-c*qPrime.z - d) / b;
} else {
qPrime.z = (-a * qPrime.x-b*qPrime.y - d) / c;
}
// Finally, compute distance (squared)
Vector3Dd=p-qPrime;
return Dot(d, d);
}
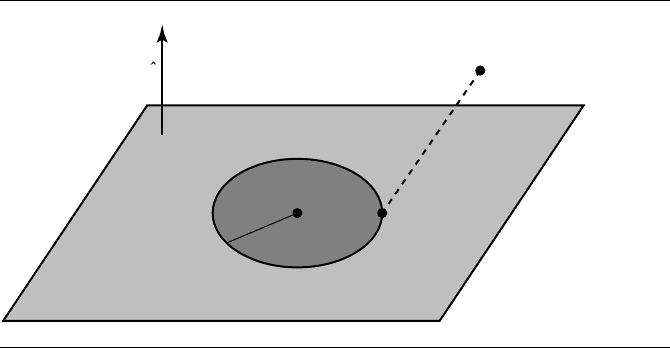
10.3.5 Point to Circle or Disk
Acirclein3DisrepresentedbyacenterC, a radius r, and a plane containing the
circle, ˆn ·(X −C) =0, where ˆn is a unit-length normal to the plane. If ˆu and ˆv are also
unit-length vectors so that ˆu, ˆv, and ˆn form a right-handed orthonormal coordinate
system (the matrix with these vectors as columns is orthonormal with determinant
1), then the circle is parameterized as
X =C + r(cos(θ ) ˆu + sin(θ) ˆv) =: C +r ˆw(θ)
for angles θ ∈ [0, 2π). Note that X − C=r, so the X values are all equidistant
from C.Moreover, ˆn · (X −C) = 0 since ˆu and ˆv are perpendicular to ˆn, so the X lie
in the plane.
For each angle θ ∈ [0, 2π), the squared distance from a specified point P to the
corresponding circle point is
F(θ)=C +r ˆw(θ) − P
2
= r
2
+C − P
2
+ 2r(C − P)·ˆw
The problem is to minimize F(θ) by finding θ
0
such that F(θ
0
) ≤ F(θ) for all θ ∈
[0, 2π). Since F is a periodic and differentiable function, the minimum must occur
when F
(θ) = 0. Also, note that (C − P) ·ˆw should be negative and as large in
magnitude as possible to reduce the right-hand side in the definition of F .The
derivative is
F
(θ) = 2r(C − P)·ˆw
(θ)
where ˆw ·ˆw
= 0 since ˆw ·ˆw =1 for all θ.Thevector ˆw
is a unit-length vector since
ˆw
=−ˆw and 0 =ˆw ·ˆw
implies 0 =ˆw ·ˆw
+ˆw
·ˆw
=−1 +ˆw
·ˆw
. Finally, ˆw
is
perpendicular to ˆn since ˆn ·ˆw =0 implies 0 =ˆn ·ˆw
. All conditions imply that ˆw is
parallel to the projection of P − C onto the plane and points in the same direction.
Let Q be the projection of P onto the plane. Then
Q − C = P − C −
ˆn · (P − C)
ˆn
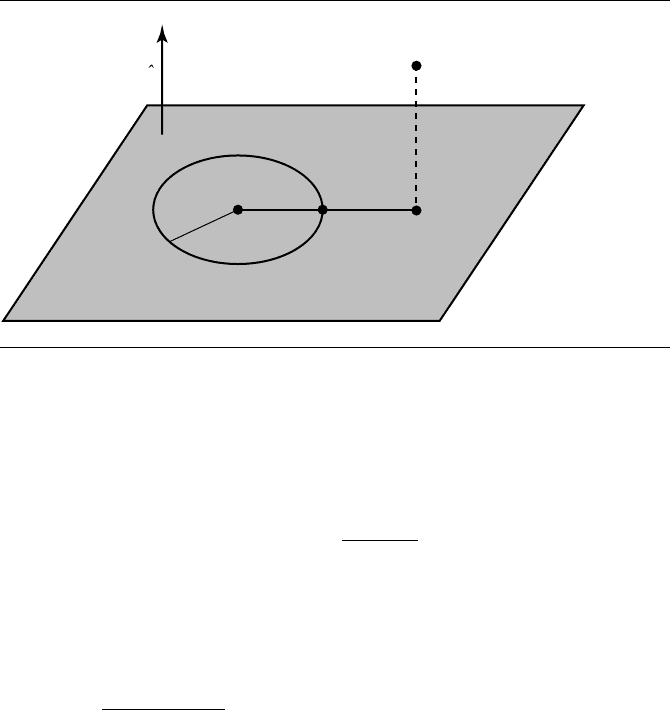
10.3 Point to Planar Component 389
C
X
P
Q
r
n
Figure 10.16 Typical case, closest point to circle.
The vector ˆw(θ) must be the unitized projection (Q − C)/Q − C. The closest
point on the circle to P is
X =C + r
Q − C
Q − C
assuming that Q = C. The distance from point to circle is then P − X.
If the projection of P is exactly the circle center C, then all points on the circle are
equidistant from C. The distance from point to circle is the length of the hypotenuse
of any triangle whose vertices are C, P , and any circle point. The lengths of the
adjacent and opposite triangle sides are r and P − C, so the distance from point
to circle is
r
2
+P − C
2
.
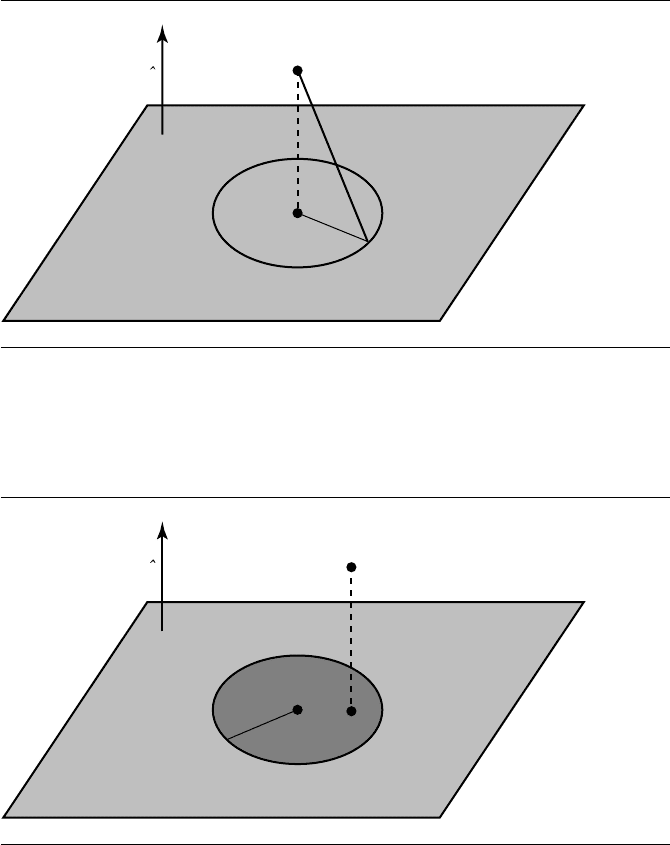
The typical case where P does not project to the circle center is shown in Figure
10.16. The case where P does project to the circle center is shown in Figure 10.17.
Point to Disk
Finding the distance from a point to a disk requires a minor modification of the
point and circle algorithm. The disk is the set of all points X = C + ρ ˆw(θ),where
0 ≤ρ ≤r. If the projection of P is contained in the disk, then the projection is already
the closest point to P . If the projection is outside the disk, then the closest point to P
is the closest point on the disk boundary, a circle. Figure 10.18 shows the case when
P projects inside the disk. Figure 10.19 shows the case when P projects outside the
disk.
390 Chapter 10 Distance in 3D
C
P
r
n
Figure 10.17 Closest point is circle center.
C
P
n
r
X
Figure 10.18
Closest point when P projects inside the disk.
10.4 Point to Polyhedron 391
C
P
n
r
X
Figure 10.19 Closest point when P projects outside the disk.
10.4 Point to Polyhedron
In this section, we address the problem of finding the distance from a point to a poly-
hedron. We first consider the general case and then address two commonly encoun-
tered specific instances—oriented bounding boxes (OBBs) and orthogonal frustums.
10.4.1 General Problem
In this section we consider the distance between a point and a polyhedron. We present
three algorithms—one for tetrahedra, one for strictly convex polyhedra, and one for
simply convex and concave polyhedra.
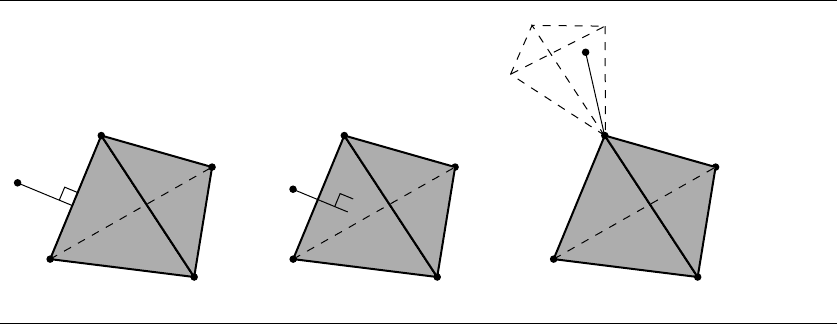
Point to Tetrahedron
We take the tetrahedron to be a special case of this problem, as we can exploit its
properties in finding its distance to a point. Consider a point P and a tetrahedron
with noncoplanar vertices V
i
for 0 ≤ i ≤ 3, as shown in Figure 10.20. The point may
be closest to an edge, to the interior of a face, or to one of the vertices (or it may
be on the interior of the tetrahedron, in which case the distance is 0). To simplify
the discussions, we assume that the vertices are ordered so that the 3 × 3 matrix M
whose columns are V
i
− V
0
for 0 ≤ i ≤ 2, in that order, has a positive determinant.
The canonical tetrahedron with this ordering is
392 Chapter 10 Distance in 3D
P
V
0
V
3
V
2
V
1
P
V
0
V
3
V
2
V
1
P
V
0
V
3
V
2
V
1
Figure 10.20 Distance from a point to a polyhedron (tetrahedron).
V
0
= (0, 0, 0)
V
1
= (1, 0, 0)
V
2
= (0, 1, 0)
V
3
= (0, 0, 1)
Outward-pointing normal vectors for the triangular faces are
n
0
= (V
1
− V
3
) × (V
2
− V
3
)
n
1
= (V
0
− V
2
) × (V
3
− V
2
)
n
2
= (V
3
− V
1
) × (V
0
− V
1
)
n
3
= (V
2
− V
0
) × (V
1
− V
0
)
Thefacetowhichn
i
is normal is the one opposite vertex V
i
and contains the vertex
V
3−i
.
The point P is inside the tetrahedron if it is on the negative side of each face plane;
that is, when n
i
· (P − V
3−i
< 0 for all i. In this case the distance will be zero. It is
possible that P is on the tetrahedron boundary itself, in which case n
i
·(P −V
3−i
) ≤
0 for all i with equality for at least one i. If an equality occurs once, the point is on a
face, but not on an edge or at a vertex. If two equalities occur, the point is on an edge,
but not at a vertex. If three equalities occur, the point is at a vertex. It is not possible
for equality to occur four times.
10.4 Point to Polyhedron 393
We know that if P is not contained within the tetrahedron, then it will have
a nonnegative distance to one, two, or three faces. Thus, we can calculate the dot
product
n
i
· (P −V
3−i
)
for i = 0, 1, 2, 3. By looking at the signs of all four dot products, we can determine
which (if any) faces the point is outside of; we then can compute the distance to
each face for which the dot product is nonnegative, and take the minimum of these
distances to be our final solution.
Point to Convex Polyhedron
If the convex polyhedron is strictly convex (no faces share a plane), then an approach
can be taken that is analogous to that taken for the tetrahedron. Let the faces be
contained in the planes n
i
· (X − V
i
) = 0, where V
i
is a vertex on the face and n
i
is an outer normal vector to the face. The point P is inside the polyhedron when
n
i
· (P − V
i
)<0 for all i. The point is outside if n
i
· (P − V
i
)>0 for some i.The
point is on the polyhedron boundary itself if n
i
· (P −V
i
) ≤ 0 for all i with equality
occurring for at least one i. If one equality occurs, the point is interior to a face. If two
equalities occur, the point is interior to an edge. If three or more equalities occur, the
point is a vertex. In this latter case, the number of equalities is the number of faces
sharing that vertex.
In any case, if we examine each face i = 0, 1, 2, ..., n − 1 in turn, and find that
all the dot products have a negative value, then P is inside the polyhedron, and
the distance is zero. Otherwise, we find one or more faces whose signed distance
is nonnegative, and we then must compute the distance between P and each such
face, and the distance is the minimum of such distances so calculated. If the faces
are triangular, then the algorithm of Section 10.3.2 can be used; otherwise, the more
general algorithm of Section 10.3.4 must be used.
Point to General Polyhedron
We start by noting that a point that is contained within a polyhedron is considered to
be at zero distance from the polyhedron. Thus, in general we can first test the point for
containment inside the polyhedron using the algorithm described in Section 13.4.3
for general polyhedra. If the point is in the polyhedron, then its distance is zero, and
no further tests need be done. Otherwise, we must then apply a method analogous to
that used in the previous section for convex polyhedra—for each face, if the point P
is on the outside of the face, find the distance from P to that face using the algorithm
of either Section 10.3.2 or Section 10.3.4 if the face is triangular or nontriangular,
respectively.
