Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

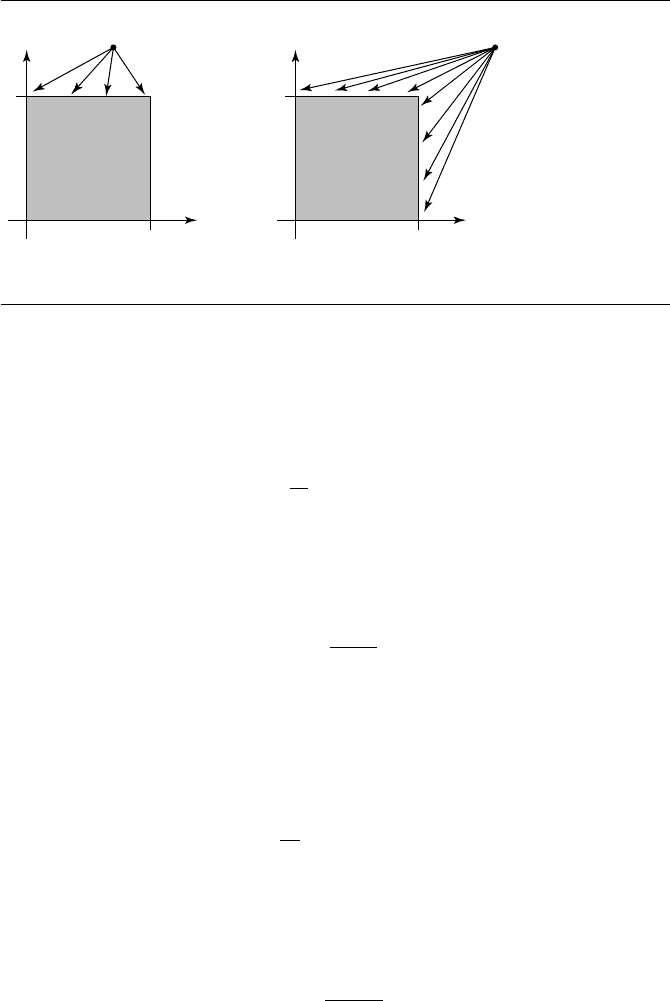
414 Chapter 10 Distance in 3D
s
t
1
1
(s
c
, t
c
)(s
c
, t
c
)
s
t
1
1
t = 1 visible
t = 1 and s = 1 visible
Figure 10.29 Definition of visibility of domain boundaries.
v
2
= (u − t
d
1
) · (u − t
d
1
),whereu = P
0
− P
1
. The derivative of this with respect
to t gives us
0 =
d
dt
v|
2
=−2
d
1
· (u − t
d
1
)
giving us a minimum at
t
=
d
1
·u
d
1
·
d
1
If 0 ≤t
≤1, then this is the actual solution; otherwise, the actual solution is 1 if t
> 1
or 0 if t
< 0.
The case for the edge t = 0 is exactly analogous: In this case we have v
2
=
(−u − s
d
0
) · (−u − s
d
0
). The derivative of this with respect to s gives us
0 =
d
ds
v|
2
=−2
d
0
· (−u − s
d
0
)
giving us a minimum at
s
=
−
d
0
·u
d
0
·
d
0

10.8 Linear Components 415
If 0 ≤s
≤1, then this is the actual solution; otherwise, the actual solution is 1 if s
> 1
or 0 if s
< 0.
In the case of edge s =1, we have v
2
= (u +
d
0
− t
d
1
) · (u +
d
0
− t
d
1
). Taking
the derivative with respect to t gives us
0 =
d
dt
v|
2
=−2
d
1
(u − t
d
1
+
d
0
)
giving us a minimum at
t
=
d
1
·u +
d
0
·
d
1
d
1
·
d
1
If 0 ≤t
≤1, then this is the actual solution; otherwise, the actual solution is 1 if t
> 1
or 0 if t
< 0.
In the case of edge t = 1, we have v
2
= (−u +
d
1
− s
d
0
) · (−u +
d
1
− s
d
0
).
Taking the derivative with respect to s gives us
0 =
d
ds
v|
2
=−2
d
0
(−u − s
d
0
+
d
1
)
giving us a minimum at
s
=
−
d
0
·u +
d
1
·
d
0
d
0
·
d
0
If 0 ≤s
≤1, then this is the actual solution; otherwise, the actual solution is 1 if s
> 1
or 0 if s
< 0.
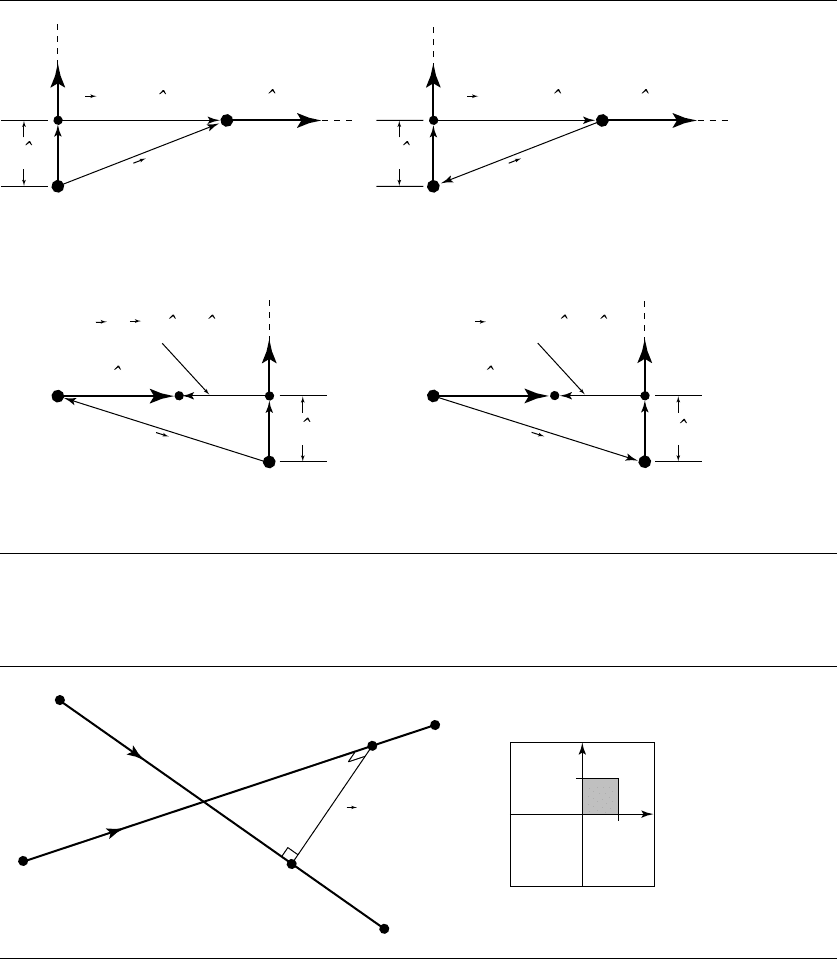
Figure 10.30 should make this more clear, but note that the figures are intended
to be schematic. It is not necessary that the two linear components be perpendicular.
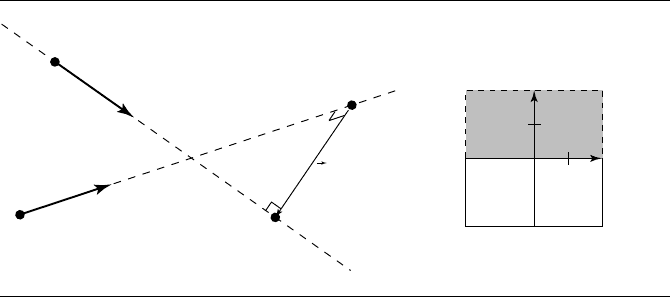
Segment to Segment
Figure 10.31 shows two line segments we want to find the distance between, and
the restricted domain for the solution. In this case, the domain of the solution is
restricted to [0, 1]×[0, 1]; the domain is bounded on all four sides: s =0, s =1, t =0,
and t = 1. If either s
c
or t
c
lies outside this region, we have to find the point on the
boundary edge of the domain that is closest to the solution point (s
c
, t
c
). The domain
416 Chapter 10 Distance in 3D
P
0
P
1
P
1
P
1
P
0
P
0
td
1
v = –u – sd
0
u
sd
0
sd
0
d
1
d
0
u
v = u – td
1
+ d
0
u
v = –u – sd
0
+ d
1
s = 0 t = 0
s = 1 t = 1
d
1
P
0
P
1
td
1
d
0
v = u – td
1
u
Figure 10.30 Cases for the four edges of the domain.
1
1
s
t
P
0
P
1
d
0
ˆ
d
1
ˆ
Q
1
Q
0
v
Figure 10.31 Distance between two line segments.
10.8 Linear Components 417
is bounded on all four sides, but clearly we need only to find the boundary point on
at most two of the edges.
The pseudocode is
float SegmentSegmentDistance3D(Segment seg0, Segment seg1)
{
u = seg0.base - seg1.base;
a = Dot(seg0.direction, seg0.direction);
b = Dot(seg0.direction, seg1.direction);
c = Dot(seg1.direction, seg1.direction);
d = Dot(seg0.direction, u);
e = Dot(seg1.direction, u);
det=a*c-b*b;
// Check for (near) parallelism
if (det < epsilon) {
// Arbitrary choice
sNum = 0;
tNum = e;
tDenom = c;
sDenom = det;
} else {
// Find parameter values of closest points
// on each segment’s infinite line. Denominator
// assumed at this point to be ‘‘det’’,
// which is always positive. We can check
// value of numerators to see if we’re outside
// the [0, 1] x [0, 1] domain.
sNum=b*e-c*d;
tNum=a*e-b*d;
}
// Check s
sDenom = det;
if (sNum < 0) {
sNum = 0;
tNum = e;
tDenom = c;
} else if (sNum > det) {
sNum = det;
tNum=e+b;
tDenom = c;
} else {
418 Chapter 10 Distance in 3D
tDenom = det;
}
// Check t
if (tNum < 0) {
tNum = 0;
if(-d<0){
sNum = 0;
} else if (-d > a) {
sNum = sDenom;
} else {
sNum = -d;
sDenom = a;
}
} else if (tNum > tDenom) {
tNum = tDenom;
if((-d+b)<0){
sNum = 0;
} else if ((-d + b) > a) {
sNum = sDenom;
} else {
sNum=-d+b;
sDenom = a;
}
}
// Parameters of nearest points on restricted domain
s = sNum / sDenom;
t = tNum / tDenom;
// Dot product of vector between points is squared distance
// between segments
v = seg0.base + (s * seg0.direction) - seg1.base + (t * seg1.direction);
return Dot(v,v);
}
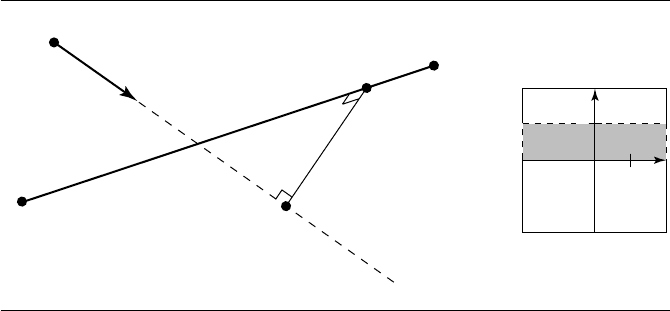
Line to Ray
Figure 10.32 shows two line segments we want to find the distance between, and the
restricted domain for the solution. In the case of a line/ray distance test, the domain
of the distance function is [−∞, ∞]× [0, ∞](or vice versa); the domain is bounded
on one side only, corresponding to either s =0ort =0. If the parameter of the closest
point on the ray’s infinite line is less than 0, then we need only compute the nearest
point along that one edge.
10.8 Linear Components 419
P
0
P
1
d
0
ˆ
d
1
ˆ
Q
0
Q
1
v
1
1
s
t
Figure 10.32 Distance between a line and a ray.
The pseudocode is
float LineRayDistance3D(Line line, Ray ray)
{
u = line.base - ray.base;
a = Dot(line.direction, line.direction);
b = Dot(line.direction, ray.direction);
c = Dot(line.direction, ray.direction);
d = Dot(line.direction, u);
e = Dot(ray.direction, u);
det=a*c-b*b;
sDenom = det;
// Check for (near) parallelism
if (det < epsilon) {
// Arbitrary choice
sNum = 0;
tNum = e;
tDenom = c;
} else {
// Find parameter values of closest points
// on each segment’s infinite line. Denominator
// assumed at this point to be ‘‘det’’,
// which is always positive. We can check
// value of numerators to see if we’re outside
// the (-inf, inf) x [0, inf) domain.
sNum=b*e-c*d;
tNum=a*e-b*d;
}
420 Chapter 10 Distance in 3D
d
1
ˆ
P
1
P
2
Q
1
1
1
s
t
Figure 10.33 Distance between a line and a line segment.
// Check t
if (tNum < 0) {
tNum = 0;
sNum = -d;
sDenom = a;
}
// Parameters of nearest points on restricted domain
s = sNum / sDenom;
t = tNum / tDenom;
// Dot product of vector between points is squared distance
// between segments
v = line.base + (s * line.direction) - s1.base + (t * ray.direction);
return Dot(v,v);
}
Line to Segment
Figure 10.33 shows two line segments we want to find the distance between, and the
restricted domain for the solution. In the case of a line/segment distance test, the
domain of the distance function is [−∞, ∞] × [0, 1] (or vice versa); the domain is
bounded on opposite sides, corresponding to either s = 0 and s = 1, or t = 0 and
t = 1. If the parameter of the closest point on the segment’s infinite line is less than 0
or greater than 1, then we need to compute the nearest point along one of those two
edges.
10.8 Linear Components 421
The pseudocode is
float LineSegmentDistance3D(Line line, Segment s)
{
u = line.base - seg.base;
a = Dot(line.direction, line.direction);
b = Dot(line.direction, seg.direction);
c = Dot(seg.direction, seg.direction);
d = Dot(line.direction, u);
e = Dot(seg.direction, u);
det=a*c-b*b;
sDenom = det;
// Check for (near) parallelism
if (det < epsilon) {
// Arbitrary choice
sNum = 0;
tNum = e;
tDenom = c;
} else {
// Find parameter values of closest points
// on each segment’s infinite line. Denominator
// assumed at this point to be ‘‘det’’,
// which is always positive. We can check
// value of numerators to see if we’re outside
// the [0,1] x [0,1] domain.
sNum=b*e-c*d;
tNum=a*e-b*d;
}
// Check t
if (tNum < 0) {
tNum = 0;
sNum = -d;
sDenom = a;
} else if (tNum > tDenom) {
tNum = tDenom;
sNum=-d+b;
sDenom = a;
}
// Parameters of nearest points on restricted domain
s = sNum / sDenom;
t = tNum / tDenom;
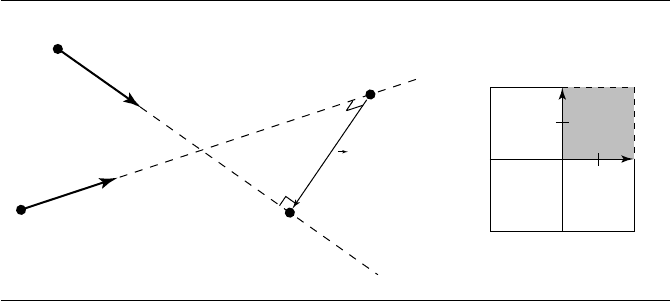
422 Chapter 10 Distance in 3D
1
1
s
t
P
1
P
0
d
0
ˆ
d
1
ˆ
Q
1
Q
0
v
Figure 10.34 Distance between two rays.
// Dot product of vector between points is squared distance
// between segments
v = line.base + (s * line.direction) - seg.base + (t * seg.direction);
return Dot(v,v);
}
RaytoRay
Figure 10.34 shows two line segments we want to find the distance between, and the
restricted domain for the solution. In the case of a ray/ray distance test, the domain
of the distance function is [0, ∞] × [0, ∞]; the domain is bounded on two adjacent
sides, corresponding to s =0 and t =0. If the parameter of the closest point on either
ray’s infinite line is less than 0, then we need to compute the nearest points on either
or both of the s = 0 and t = 0 edges.
The pseudocode is
float RayRayDistance3D(Ray ray0, Ray ray1)
{
u = ray0.base - ray1.base;
a = Dot(ray0.direction, ray0.direction);
b = Dot(ray0.direction, ray1.direction);
c = Dot(ray1.direction, ray1.direction);
d = Dot(ray0.direction, u);
e = Dot(ray1.direction, u);
det=a*c-b*b;
// Check for (near) parallelism
10.8 Linear Components 423
if (det < epsilon) {
// Arbitrary choice
sNum = 0;
tNum = e;
tDenom = c;
sDenom = det;
} else {
// Find parameter values of closest points
// on each segment’s infinite line. Denominator
// assumed at this point to be ‘‘det’’,
// which is always positive. We can check
// value of numerators to see if we’re outside
// the [0, inf) x [0, inf) domain.
sNum=b*e-c*d;
tNum=a*e-b*d;
}
// Check s
sDenom = det;
if (sNum < 0) {
sNum = 0;
tNum = e;
tDenom = c;
}
// Check t
if (tNum < 0) {
tNum = 0;
if(-d<0){
sNum = 0;
} else {
sNum = -d;
sDenom = a;
}
}
// Parameters of nearest points on restricted domain
s = sNum / sDenom;
t = tNum / tDenom;
// Dot product of vector between points is squared distance
// between segments
v = ray0.base + (s * ray0.direction) - ray1.base + (t * ray1.direction);
return Dot(v,v);
}
