Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

374 Chapter 10 Distance in 3D
P
n
Q
Q´
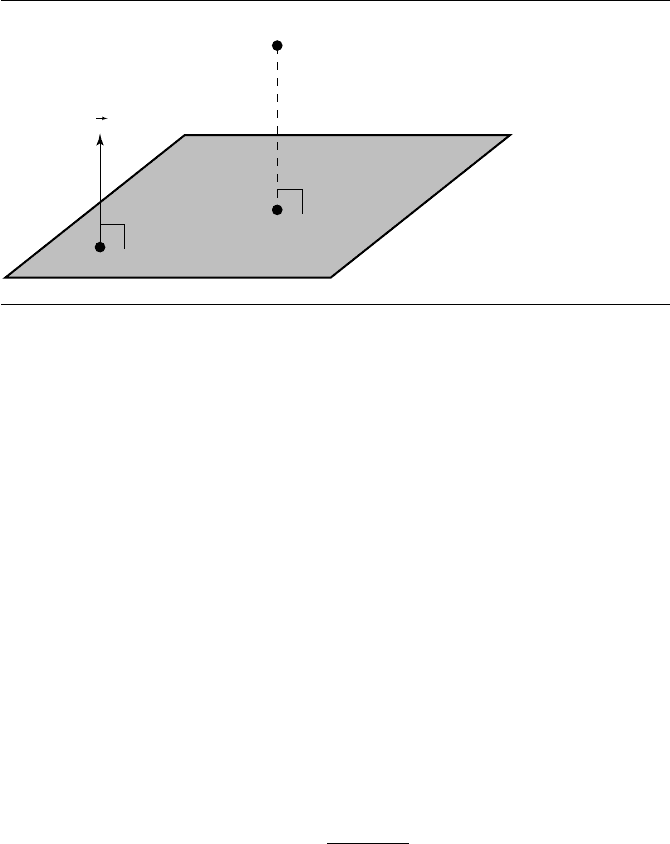
Figure 10.6 Distance between a point and a plane.
10.3
Point to Planar Component
In this section, we discuss the problem of computing the distance between a point
and planar components—planes, triangles, rectangles, polygons, circles, and disks.
10.3.1 Point to Plane
In this section, we consider the distance from a point Q to a plane P : {P , n},wheren
is a normal vector of the plane and P is a point on P (Section 9.2.1); see Figure 10.6.
The point on the plane P closest to Q is denoted Q
. Note that the vector between
Q and Q
is perpendicular to P (that is, parallel to n), and we can exploit this fact in
determining the distance from Q to P.
Figure 10.7 shows an edge-on view of plane P. From trigonometry, we can ob-
serve that
cos θ =
Q − Q
Q − P
So we have
d =Q − Q
=Q − P cos θ
(10.3)
By definition, u ·v =uv cos θ, so we can rewrite Equation 10.3 as

10.3 Point to Planar Component 375
P
Q
Q'
r
n
Figure 10.7 Edge-on view of plane P.
d =Q − P cos θ
=Q − P
−kn ·−(Q − P)
knQ − P
=
|n · (Q − P)|
n
If the plane’s normal is unit length, then the denominator is 1, and no division is
required.
In some situations, the side of a plane that a point is on may be important. In
this case, the signed distance (the sign being relative to the plane normal) may be
required. A simple algorithm (Georgiades 1992) exists for finding this signed distance
if the plane equation is normalized. If we have a plane P in the “vector version” of
the implicit form
P ·ˆn + d = 0
and a point Q, then the line connecting the projection Q
of Q onto P is parallel to
ˆn. If the plane normal is normalized, then Q − Q
is a scalar multiple of ˆn; that is,
that scalar multiple is the distance.
Following Georgiades (1992), the derivation is as follows: Let r =Q −Q
; then
Q = r ˆn + Q
If we multiply both sides by ˆn,wehave
ˆn · Q = r ˆn ·ˆn +ˆn · Q
(10.4)
376 Chapter 10 Distance in 3D
V
0
V
2
P
P´
V
0
V
1
V
2
P
P´
V
1
(a) (b)
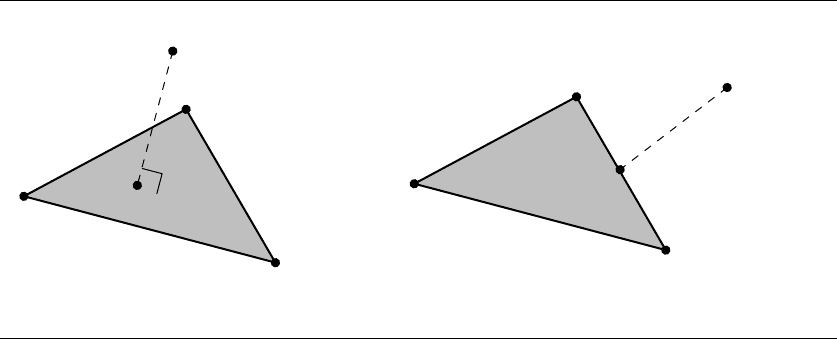
Figure 10.8 Distance between a point and a triangle. The closest point may be on the interior of the
triangle (a), on an edge (b), or be one of the vertices.
However, ˆn=1 because of the assumption of normalization. Further, ˆn · Q
=−d
because Q
is on the plane by definition. If we substitute these back into Equa-
tion 10.4, we get
r =ˆn · Q + d
Thus, the distance from Q to plane P is r, and the sign of r is positive if Q is on the
side of P toward which the normal points and negative if it is on the other side.
10.3.2 Point to Triangle
In this section, we discuss the problem of finding the distance between a point P
and a triangle, as shown in Figure 10.8. For the purposes of this section, we define a
triangle T with vertices {V
0
, V
1
, V
2
} parametrically
T (s, t) = B + s e
0
+ t e
1
for (s, t) ∈ D ={(s, t) : s ∈ [0, 1], t ∈ [0, 1], s + t ≤ 1}, B = V
0
, e
0
= V
1
− V
0
, and
e
1
= V
2
− V
0
. The minimum distance is computed by locating the values (¯s,
¯
t) ∈ D
corresponding to the point P
, the closest point on the triangle to P .
The distance from any point on the triangle to P is
T (s, t) − P

10.3 Point to Planar Component 377
but we use instead the squared-distance function
Q(s, t) =T (s, t) − P
2
for (s, t) ∈ D. If we expand the terms and multiply them out, we can see that this
function is quadratic in s and t:
Q(s, t) = as
2
+ 2bst + ct
2
+ 2ds + 2et + f
where
a =e
0
·e
0
b =e
0
·e
1
c =e
1
·e
1
d =e
0
· (B − P)
e =−e
1
· (B − P)
f = (B − P)· (B − P)
Quadratics are classified by the sign of ac −b
2
.ForQ
ac − b
2
= (e
0
·e
0
)(e
1
·e
1
) − (e
0
·e
1
)
2
=e
0
×e
1
2
> 0
This value is positive because we assume that the two edges e
0
and
d
1
of the triangle
are linearly independent (that is, not parallel and neither having zero length). Thus,
their cross product is a nonzero vector.
In calculus terms, the goal is to minimize Q(s, t) over the domain D. Since Q is a
continuously differentiable function, the minimum occurs either at an interior point
of D where the gradient ∇Q = 2(as + bt + d, bs +ct + e) = (0, 0) (that is, inside
the triangle) or at a point on the boundary of D.
The gradient of Q is zero only when
¯s =
be − cd
ac − b
2
and
¯
t =
bd −ad
ac − b
2
378 Chapter 10 Distance in 3D
2
4
1
56
3
0
s
t
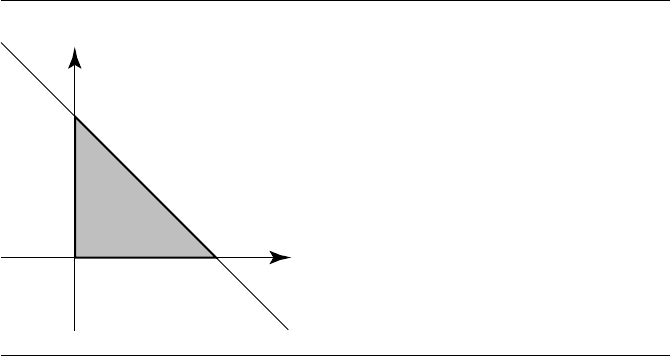
Figure 10.9 Partition of the st-plane by triangle domain D.
If (¯s,
¯
t) ∈ D, then we have found the minimum of Q. Otherwise, the minimum
must occur on the boundary of the triangle. To find the correct boundary, consider
Figure 10.9. The central triangle labeled 0 is the domain of Q, (s, t) ∈ D.If(¯s,
¯
t) is
in region 0, then P
, the point on the triangle closest to P , is on the interior of the
triangle.
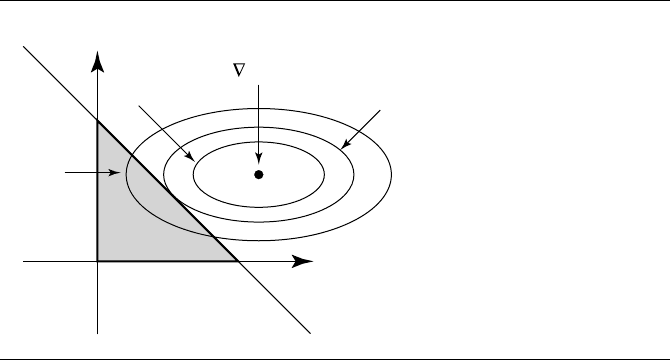
Suppose (¯s,
¯
t) is in region 1. The level curves of Q are those in the st-plane
for which Q is a constant. Since the graph of Q is a paraboloid, the level curves
are ellipses (see Section A.9.1). At the point where ∇Q = (0, 0), the level curve
degenerates to a single point (¯s,
¯
t). The global minimum of Q occurs there; call
it V
min
. As the level values V increase from V
min
, the corresponding ellipses are
increasingly further away from (¯s,
¯
t). There is a smallest level value V
0
for which
the corresponding ellipse (implicitly defined by Q = V
0
) just touches the triangle
domain edge s + t = 1 at a value s = s
0
∈ [0, 1], t
0
= 1 − s
0
. For level values V<V
0
,
the corresponding ellipses do not intersect D. For level values V>V
0
, portions of D
lie inside the corresponding ellipses. In particular, any points of intersection of such
an ellipse with the edge must have a level value V>V
0
. Therefore, Q(s,1− s) >
Q(s
0
, t
0
) for s ∈ [0, 1] and s = s
0
. The point (s
0
, t
0
) provides the minimum squared
distance between P and the triangle. The triangle point is an edge point. Figure 10.10
illustrates the idea by showing various level curves.
An alternative way of visualizing where the minimum distance point occurs on
the boundary is to intersect the graph of Q, which lives in (s, t, Q) space, with the
plane s + t = 1. The curve of intersection is a parabola and is the graph of F(s)=
Q(s,1− s) for s ∈ [0, 1]. Now the problem has been reduced by one dimension to
minimizing a function F(s) for s ∈ [0, 1]. The minimum of F occurs either at an
10.3 Point to Planar Component 379
s
t
Q > V
0
Q < V
0
Q = V
0
Q = 0
Figure 10.10 Various level curves Q(s, t)= V .
interior point of [0, 1], in which case F
(s) = 0 at that point, or at an end point s =0
or s =1. Figure 10.10 shows the case when the minimum occurs at an interior point.
At that point the ellipse is tangent to the line s + t = 1. In the end point cases, the
ellipse may just touch one of the vertices of D, but not necessarily tangentially.
To distinguish between the interior point and end point cases, the same partition-
ing idea applies in the one-dimensional case. The interval [0, 1]partitions the real line
into three intervals: s<0, s ∈ [0, 1], and s>1. Let F
(ˆs) = 0. If ˆs<0, then F(s) is
an increasing function for s ∈[0, 1]. The minimum restricted to [0, 1]must occur at
s = 0, in which case Q attains its minimum at (s, t) = (0, 1).If
ˆ
(s) > 1, then F(s)
is a decreasing function for s ∈ [0, 1]. The minimum for F occurs at s = 1, and the
minimum for Q occurs at (s, t) =(1, 0). Otherwise, ˆs ∈[0, 1], F attains its minimum
at ˆs, and Q attains its minimum at (s, t) = (ˆs,1−ˆs).
The occurrence of (¯s,
¯
t)in region 3 or region 5 is handled in the same way as when
the global minimum is in region 0. If (¯s,
¯
t) is in region 3, then the minimum occurs
at (s
0
,0) for some s
0
∈[0, 1]. Determining if the first contact point is at an interior or
end point of the appropriate interval is handled the same as discussed earlier.
If (¯s,
¯
t) is in region 2, it is possible the level curve of Q that provides first contact
with the unit square touches either s + t = 1 or edge s =0. Because the global min-
imum occurs in region 2, and because the level sets of Q are ellipses, at least one of
the directional derivatives (0, −1) ·∇Q(0, 1) and (1, −1) ·∇Q(0, 1) must be positive.
The two vectors (0, −1) and (1, −1) are directions for the edges s = 0 and s + t = 1,
respectively. The choice of edges s +t = 1ors =0 can be made based on the signs of
(0, −1) ·∇Q(0, 1) and (1, −1) ·∇Q(0, 1).
380 Chapter 10 Distance in 3D
The same type of argument applies in region 6. In region 4, the two quantities
whose signs determine which edge contains the minimum are (1, 0) ·∇Q(0, 0) and
(0, 1) ·∇Q(0, 0).
The implementation of the algorithm is designed so that at most one floating-
point division is used when computing the minimum distance and corresponding
closest points. Moreover, the division is deferred until it is needed. In some cases, no
division is required.
Quantities that are used throughout the code are computed first. In particular,
the values computed are
d = B − P
a =e
0
·e
0
b =e
0
·e
1
c =e
1
·e
1
d =e
0
·
d
e =e
1
·
d
f =
d ·
d
The code actually computes σ =|ac − b
2
| since it is possible for small edge lengths
that some floating-point round-off errors lead to a small negative quantity.
In the theoretical development, we compute ¯s = (be − cd)/σ and
¯
t = (bd −
ae)/σ so that ∇Q(¯s,
¯
t) = (0, 0). The location of the global minimum is then tested
to see if it is in the triangle domain D. If so, then we have already determined what
we need to compute the minimum distance. If not, then the boundary of D must
be tested. To defer the division by σ , the code instead computes ¯s = be − dc and
¯
t = bd − ae and tests for containment in a scaled domain: s ∈ [0, σ ], t ∈ [0, σ ], and
s + t ≤ σ . If in that set, then the divisions are performed. If not, then the boundary
of the unit square is tested. The general outline of the conditionals for determining
which region contains (¯s,
¯
t) is
det = a*c - b*b; s = b*e - c*d; t = b*d - a*e;
if(s+t<=det) {
if(s<0){
if(t<0){
region 4
} else {
region 3
}
}
} else {
10.3 Point to Planar Component 381
if(s<0){
region 2
} else if (t < 0) {
region 6
} else {
region 1
}
}
The block of code for handling region 0 is
invDet=1/det;
s *= invDet;
t *= invDet;
and requires a single division.
The block of code for region 1 is
// F(s)=Q(s,1-s)=(a-2b+c)s^2 + 2(b-c+d-e)s+(c+2e+f)
// F’(s)/2 = (a - 2b + c)s + (b-c+d-e)
// F’(s}=0whens=(c+e-b-d)/a-2b+c)
// a-2b+c=|e0-e1|^2 > 0,
// so only the sign ofc+e-b-dneed be considered
numer=c+d-b-d;
if (numer <= 0) {
s=0;
} else {
denom=a-2*b+c; //positive quantity
s = (numer >= denom ? 1: numer/denom);
}
t=1-s;
The block of code for region 3 is given below. The block for region 5 is similar.
// F(t) = Q(0, t) = ct^2 + et + f
// F’(t)/2 = ct + e
// F’(t) = 0 when t = -e/c
s=0;
t=(e>=0?0:(-e>=c?1:-e/c));
The block of code for region 2 is given below. Blocks for regions 4 and 6 are
similar.
382 Chapter 10 Distance in 3D
P
0
P
1
P
2
P
3
e
0
e
1
Figure 10.11 Alternative definition of a rectangle.
// Grad{Q} = 2(as + bt + d, bs + ct + e)
// (0, -1) * Grad(Q(0, 1)) = (0, -1) * (b + d,c+e)=-(c+e)
// (1, -1) * Grad(Q(0, 1)) = (1, -1) * (b + d,c+e)=(b+d)-(c+e)
// minonedges+t=1if(1,-1)*Grad(Q(0, 1)) < 0)
// minonedges=0otherwise
tmp0=b+d;
tmp1=c+e;
if (tmp1 > tmp0) { // min on edges+t=1
numer = tmp1 - tmp0;
denom=a-2*b+c;
s = (numer >= denom? 1 : numer / denom);
t=1-s;
} else {
s=0;
t = (tmp1 <=0?1:(e>=0?0:-e/c));
}
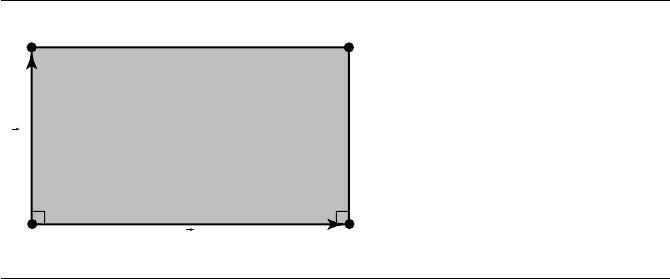
10.3.3 Point to Rectangle
Typically, a rectangle is defined by a list of four vertices P
0
, P
1
, P
2
, and P
3
.However,
if we let P = P
0
and define e
0
= P
1
− P and e
1
= P
3
− P , then a rectangle can
be equivalently defined as R(s, t) = P + s e
0
+ t e
1
for (s, t) ∈ [0, 1]
2
, as shown in
Figure 10.11.
Given a point Q and a rectangle R, we wish to find the distance from Q to Q
, the
closest point of R to Q, as shown in Figure 10.12. The closest point on the rectangle
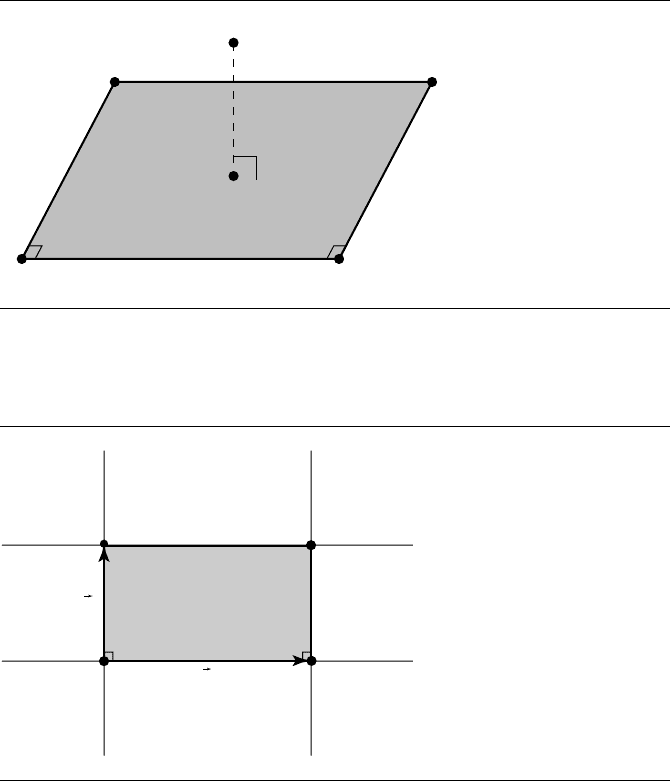
10.3 Point to Planar Component 383
Q
Q'
P
2
P
3
P
0
P
1
Figure 10.12 Distance between a point and a rectangle.
e
1
24
15
6
3
0
78
P
0
P
1
P
3
P
2
e
0
Figure 10.13 Partition of the plane by a rectangle.
to Q is obtained by projecting Q onto the plane containing R, and then analyzing
the relationship of Q
to the vertices and edges of R.IfQ
is in the interior of R,
then that is the closest point; however, if Q
is on the exterior of R, then the closest
point is instead either a vertex of R or a point on an edge of R. The vectors e
0
and
e
1
are orthogonal and, if extended outside the range [0, 1], can be seen to divide the
plane into nine regions, as shown in Figure 10.13.
