Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

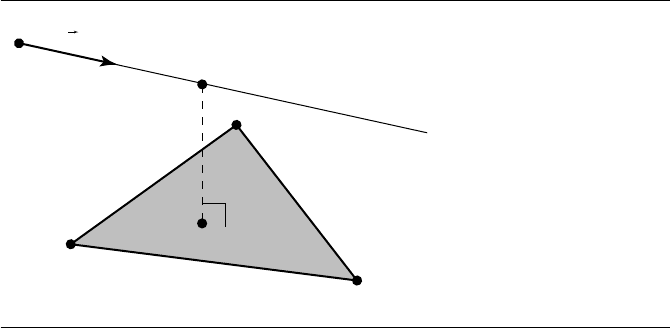
434 Chapter 10 Distance in 3D
V
0
V
1
V
2
Q
P
d
Figure 10.38 Distance between a line and a triangle.
are typically represented as three vertices V
0
, V
1
, and V
2
. For the purposes of this
problem, however, we use a parametric representation:
T (u, v) =V + ue
0
+ ve
1
where V is a vertex of the triangle, say, V
0
, and e
0
= V
1
− V
0
and e
1
= V
2
− V
0
.Any
point in the triangle can then be described in terms of the two parameters u and v,
with 0 ≤ u, v ≤ 1, and u + v ≤ 1 (see Figure 10.39). Computing the distance between
the linear component and the triangle means that we must find the values of t, u, and
v that minimize the (squared) distance function
Q(u, v, t) =T (u, v) − L(t)
2
Expanding terms and multiplying, we get
Q(u, v, t) =T (u, v) − L(t)
2
= (e
0
·e
0
)u
2
+ (e
1
·e
1
)v
2
+ (
d ·
d)t
2
+ 2(e
0
·e
1
)uv + 2(−e
0
·
d)ut + 2(−e
1
·
d)vt
+ 2(e
0
· (V − P ))u + 2(e
1
· (V − P ))v + 2(−
d · (V − P ))t
+ (V − P)· (V − P)
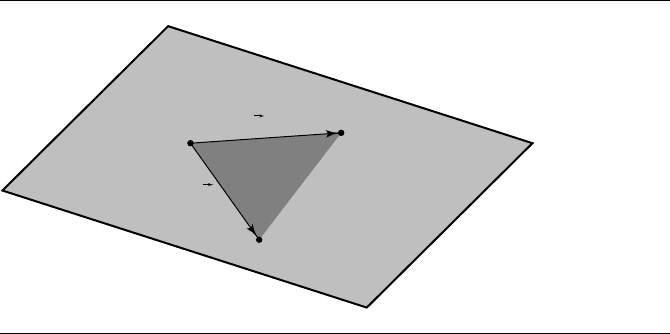
10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 435
V
0
V
1
V
2
e
0
e
1
Figure 10.39 Parametric representation of a triangle.
or, more compactly
Q(u, v, t) = a
00
u
2
+ a
11
v
2
+ a
22
t
2
+ 2a
01
uv + 2a
02
ut + 2a
12
vt +2b
0
u
+ 2b
1
v + 2b
2
t + c (10.14)
where
a
00
=e
0
·e
0
a
11
=e
1
·e
1
a
22
=
d ·
d
a
01
=e
0
·e
1
a
02
=−e
0
·
d
a
12
=−e
1
·
d
b
0
=e
0
· (V − P)
b
1
=e
1
· (V − P)
b
2
=−
d · (V − P)
c = (V − P)· (V − P)
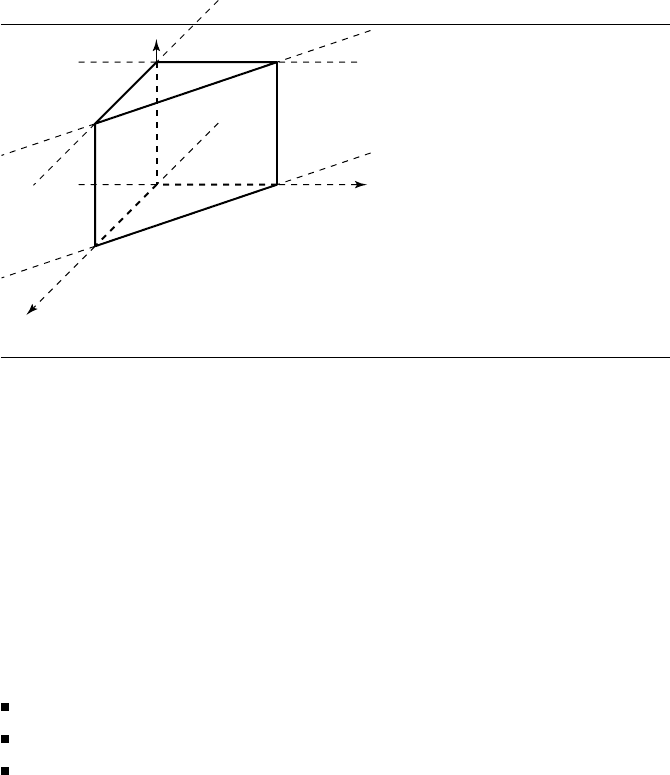
436 Chapter 10 Distance in 3D
u
v
t
0
1
234
5
6
Figure 10.40 Possible partitionings of the solution space for the linear component/triangle dis-
tance problem.
As the solution to this consists of three values (u
0
, v
0
, t
0
), we can think of the
solution space as three spatial dimensions (not to be confused with the 3D space
in which the linear component and the triangle lie). This is analogous to the parti-
tioning of the two-dimensional solution space domain in the point-triangle distance
test shown in Figure 10.9, except that we now have a third dimension correspond-
ing to the parameter t of the linear component. For linear components, we have
three possible domains, and so there are three possible partitionings of the solution
space:
Line: an infinite triangular prism
Line segment: a finite triangular prism
Ray: a semi-infinite triangular prism
The case for a line segment is shown in Figure 10.40.
If the configuration of the triangle and linear component are such that the point
on the plane containing the triangle that is nearest to the linear component actually
lies within the triangle, and the point on the linear segment nearest the triangle is
within the bounds (if any) of the linear segment, then the solution ( ¯u, ¯v,
¯
t) will lie
within region 0 of the solution domain’s triangular prism; the distance between the
linear segment and the triangle will be T ( ¯u, ¯v,
¯
t)−L(t). Otherwise, the minimum
of ∇Q = ( ¯u, ¯v,
¯
t) will be on a face separating the regions (and where it lies on a face
may be along an edge or vertex of the boundaries between regions).
The first step in the algorithm is to find the values of u, v, and t that minimize
the squared-distance function of Equation 10.14. Formally, we must find where the
10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 437
gradient ∇Q = 0; this can be expressed as finding the solution to the system of
equations
a
00
a
01
a
02
a
10
a
11
a
12
a
20
a
21
a
22
b
0
b
1
b
2
=
u
v
t
which can be done by inverting the 3 ×3 matrix. As noted in Section 2.5.4, a matrix
must have a nonzero determinant in order for it to be invertible; in this case, the
determinant is zero if and only if the linear component and the plane are parallel,
and so we handle this as a special case.
For each type of linear component, the first step is to find the determinant of
the system, and if it is nonzero, to then compute the solution in order to find the
region in which the solution lies. Once the region has been determined, calculations
specific to that region are made in order to find the point ( ¯u, ¯v,
¯
t) on the boundary
that represents the minimum.
Line to Triangle
For the line to triangle distance, the solution domain breaks up the domain into six
regions. The pseudocode to determine the region is as follows:
float LineTriangleDistanceSquared(Line line, Triangle triangle)
{
e0 = triangle.v[1] - triangle.v[0];
e1 = triangle.v[2] - triangle.v[0];
a00 = Dot(e0, e0);
a01 = Dot(e0, e1);
a02 = -Dot(e0, line.direction);
a11 = Dot(e1, e1);
a12 = -Dot(e1, line.direction);
a22 = Dot(line.direction, line.direction);
diff = triangle.v[0] - line.base;
b0 = Dot(e0, diff);
b1 = Dot(e1, diff);
b2 = -Dot(line.direction, diff);
c = Dot(diff, diff);
// Cofactors to be used for determinant
// and inversion of matrix A
cof00 = a11 * a22 - a12 * a12;
cof01 = a02 * a12 - a01 * a22;
cof02 = a01 * a12 - a02 * a11;
438 Chapter 10 Distance in 3D
det = a00 * cof00 - a01 * cof01 + a02 * cof02;
// Invert determinant and b if det is negative --
// Avoids having to deal with special cases later.
if (det < 0) {
det = -det;
b0 = -b0;
b1 = -b1;
b2 = -b2;
}
// Check if determinant is (nearly) 0
if (det < epsilon) {
// Treat line and triangle as parallel. Compute
// closest points by computing distance from
// line to each triangle edge and taking minimum.
Segment seg0 = {triangle.v[0], triangle.v[1] };
dist0 = LineLineSegDistanceSquared(line, seg0);
Segment seg1 = {triangle.v[0], triangle.v[1] };
dist1 = LineLineSegDistanceSquared(line, seg1);
Segment seg2 = {triangle.v[1], triangle.v[2] };
dist2 = LineLineSegDistanceSquared(line, seg2);
distance = MIN(dist0, MIN(dist1, dist2));
return distance;
} else {
// Determine the region in which solution lies by
// computing u and v and checking their signs
cof11 = a00 * a22 - a02 * a02;
cof12 = a02 * a01 - a00 * a12;
u = -(cof00 * b0 + cof01 * b1 + cof02 * b2);
v = -(cof01 * b0 + cof11 * b1 + cof12 * b2);
if(u+v<=det) {
if(u<0){
if(v<0){
region 4
} else {
region 3
}
} else if (v < 0) {
10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 439
region 5
} else {
region 0
}
} else {
if(u<0){
region 2
} else if (v < 0) {
region 6
} else {
region 1
}
}
}
}
The pseudocode for region 0 is
invDet=1/det;
u=u*invDet;
v=v*invDet;
cof22 = a00 * a11 - a01 * a01;
r = -(cof02 * b0 + cof12 * b1 + cof22 * b2) * invDet;
The code for the other regions is more complex. Consider the code for re-
gion 3—here, ¯u = 0. If we substitute this back into Equation 10.14, the original
squared-distance formula, terms involving u drop out, and we have effectively a
lower-dimension quadratic equation to solve:
Q
1
(v, t) = a
11
v
2
+ a
22
t
2
+ 2a
12
vt +2b
1
v + 2b
2
t + c, v, t ∈ [0, 1] ×(−∞, ∞)
The region consists of an infinite strip bounded v =0 and v =1 lying in the (v, t)
plane, and two half-planes, shown “looking down the t -axis” in Figure 10.41. The
solution ( ¯v,
¯
t) to ∇Q
1
is computed; v may lie either in the infinite strip or on one of
the two half-planes. If it lies in the infinite strip (i.e., 0 ≤¯v ≤ 1, then the solution to
Q is (0, ¯v,
¯
t). Otherwise, it lies on one or the other half-plane, and the minimum will
then be on the line at the intersection of the infinite strip and the half-planes (where
v = 0orv = 1). If v =0, then the quadratic equation resulting from dropping out
termsofbothu and v of Equation 10.14 is
Q
2
(t) = a
22
t
2
+ 2b
2
t + c, t ∈ (−∞, ∞)
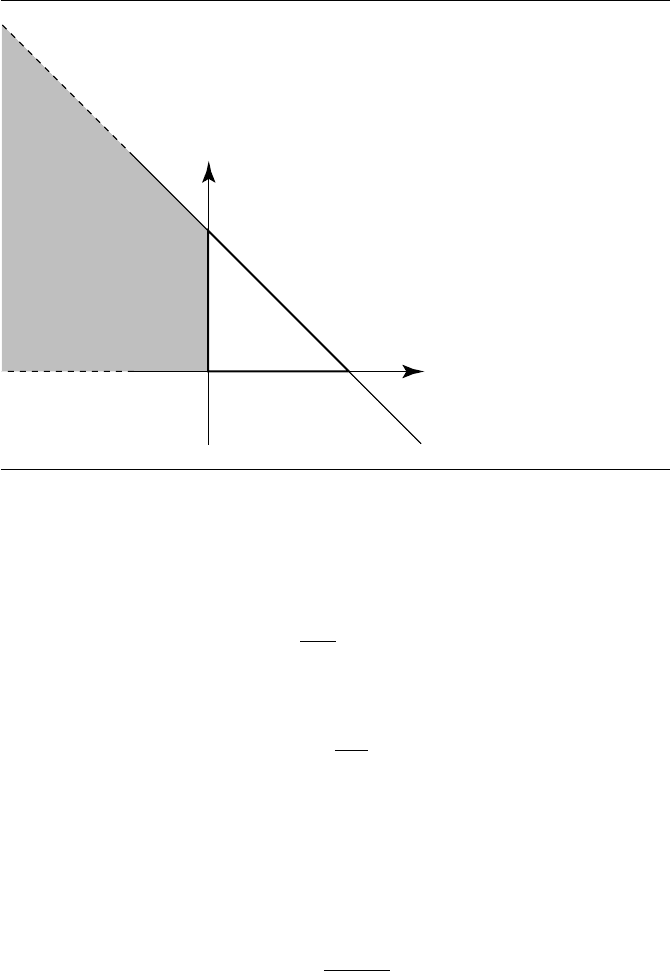
440 Chapter 10 Distance in 3D
2
4
1
56
3
0
u
v
Figure 10.41 Boundary strip and planes for region 3.
whose solution occurs when
dQ
2
dt
= 0
so
t =
−b
2
a
22
If ¯v>1, then the quadratic to minimize is
Q
3
= a
22
t
2
+ 2(a
12
+ b
2
)t + (a
11
+ 2b
1
+ c)
so
t =−
a
12
+ b
2
a
22
.
10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 441
The pseudocode for this is
u=0;
v=a12*b2-a22*b1;
if (t >= 0) {
if (t <= det) {
invDet=1/cof00;
v *= invDet;
t = (a12 * b1 - a22 * b2) * invDet;
} else {
v=1;
t = -(b2 + a12) / a22;
}
} else {
v=0;
t = -b2 / a22;
}
The analysis and associated code for regions 1 and 5 are similar to that for region
3. The analysis and code for regions 2, 4, and 6 are a bit simpler because we only
have two half-planes against which to test: we have (u = 0, v =1), (u =0, v = 0), and
(u = 1, v = 0), respectively, for each of these regions.
Ray to Triangle and Segment to Triangle
The basic approach for the ray/triangle and segment/triangle distance problems is
exactly analogous to that just presented for line/triangle distance. However, in the
former case, instead of having 6 regions in the domain, we have 12 (the same 6 as
for the line/triangle case, but doubled because the ray divides its infinite line into 2
regions—t<0 and t ≥ 0); in the latter case, we have 18 regions—three sets of the
same 6 for t<0, 0 ≤ t ≤ 1, and t>1.
10.9.2 Linear Component to Rectangle
In this section we consider the problem of finding the distance between a linear
component and a rectangle, as shown in Figure 10.42. The linear component is
represented in the usual fashion, by a base point and direction vector: L(t) =P +t
d.
Typically, a rectangle is considered to be defined by four vertices V
0
, V
1
, V
2
, and V
3
.
However, as for the problem of the linear component/triangle distance problem, we
utilize an alternative representation, consisting of a vertex and two vectors defining
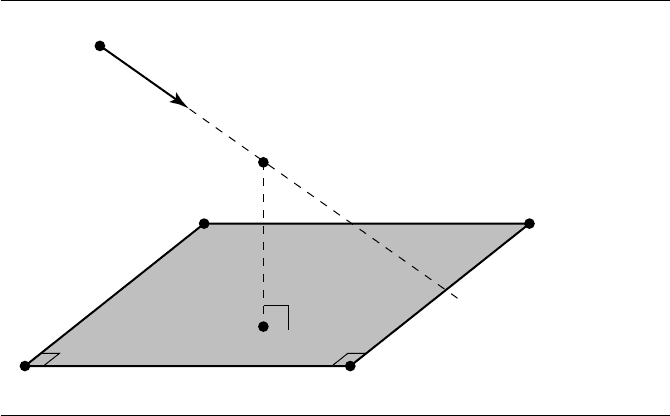
442 Chapter 10 Distance in 3D
V
0
V
3
V
2
V
1
Q
d
ˆ
P
Figure 10.42 Distance between a line and a rectangle.
the edges incident on the vector. Arbitrarily, we choose V
0
as the “origin,” giving us
a rectangle {V , e
0
, e
1
},whereV = V
0
, e
0
= V
1
− V
0
, and e
1
= V
3
− V
0
, as shown in
Figure 10.13. This gives us a parametric rectangle as R(u, v) = V + ue
0
+ ve
1
with
0 ≤u, v ≤ 1.
Given this, our squared-distance function is
Q(u, v, t) =R(u, v) − L(t).
Substituting in the formulas for the linear component and rectangle, we get
Q(u, v, t) = (e
0
·e
0
)u
2
+ (e
1
·e
1
)v
2
+ (
d ·
d)t
2
+ (e
0
·e
1
)uv + (−e
0
·
d)ut + (−e
1
·
d)vt
+ 2(e
0
· (V − P ))u + 2(e
1
· (V − P ))v + 2((V − P)· (V − P ))t + c
or, more compactly,
Q(u, v, t) = a
00
u
2
+ a
11
v
2
+ a
22
t
2
+ a
01
uv + a
02
ut + a
12
vt +2b
0
u
+ 2b
1
v + 2b
2
t + c (10.15)
10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 443
where
a
00
=e
0
·e
0
a
01
=e
0
·e
1
a
11
=e
1
·e
1
a
12
=−e
0
·
d
a
02
=−e
0
·
d
a
12
=−e
1
·
d
a
22
=
d ·
d
b
0
=e
0
· (V − P)
b
1
=e
1
· (V − P)
b
2
= (V − P)· (V − P)
The domain of Q is R
3
and is partitioned similarly to Figure 10.40, but instead
defines either an infinite square column, a semi-infinite square column, or a cube,
for the cases of lines, rays, and segments, respectively. The partitioning for the line
segment case is shown in Figure 10.43. If the configuration of the rectangle and
linear component are such that the point on the plane containing the rectangle that
is nearest to the linear component actually lies within the rectangle, and the point
on the linear segment nearest the rectangle is within the bounds (if any) of the
linear segment, then the solution ( ¯u, ¯v,
¯
t) will lie within region 0 of the solution
domain’s cube; the distance between the linear segment and the rectangle will be
T ( ¯u, ¯v,
¯
t) − L(t). Otherwise, the minimum of ∇Q = ( ¯u, ¯v,
¯
t) willbeonaface
separating the regions (and where it lies on a face may be along an edge or vertex of
the boundaries between regions).
The first step in the algorithm is to find the values of u, v, and t that minimize
the squared-distance function of Equation 10.15. Formally, we must find where the
gradient ∇Q = 0; this can be expressed as finding the solution to the system of
equations
a
00
a
01
a
02
a
10
a
11
a
12
a
20
a
21
a
22
b
0
b
1
b
2
=
u
v
t
which can be done by inverting the 3 ×3 matrix. As noted in Section 2.5.4, a matrix
must have a nonzero determinant in order for it to be invertible; in this case, the
determinant is zero if and only if the linear component and the plane are parallel,
and so we handle this as a special case.
