Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

454 Chapter 10 Distance in 3D

Here, the squared distance is simply the sum of the squared distances in y and z:













+ extent



< −extent



− extent



> extent

0 otherwise









+ extent



< −extent



− extent



> extent

0 otherwise

(Note that if the line intersects the box, the distance is 0.)

The closest point on the line is (arbitrarily, but consistently) chosen to correspond

to the “positive” YZ face of the box:

t =

extent

− P







The closest point on the box is (again arbitrarily, but consistently) chosen to be

on the box’s “positive” YZ face; the point will be within that face if the line intersects

the box, and either along one of the edges or at a corner if it does not.

The pseudocode is

real CaseTwoZeroComponents_YZ(Line line, OBB box, real t)

{

real distanceSquared = 0;

// Parameter of closest point on the line

t = (box.extents.x - line.origin.x) / line.direction.x;

// Closest point on the box

qPrime.x = box.extents.x;

qPrime.x = line.origin.y;

qPrime.x = line.origin.z;

// Compute distance squared and Y and Z components

// of box’s closest point

if (line.origin.y < - box.extents.y) {

delta = line.origin.y + box.extents.y;

distanceSquared += delta * delta;

qPrime.y = -box.extents.y;

} else if (line.origin.y > box.extents.y) {

delta = line.origin.y - box.extents.y;

distanceSquared += delta * delta;

10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 455

qPrime.y = box.extents.y;

}

if (line.origin.z < - box.extents.z) {

delta = line.origin.z + box.extents.z;

distanceSquared += delta * delta;

qPrime.z = -box.extents.z;

} else if (line.origin.z > box.extents.z) {

delta = line.origin.z - box.extents.z;

distanceSquared += delta * delta;

qPrime.z = box.extents.z;

}

return distanceSquared;

}

One Zero-Component

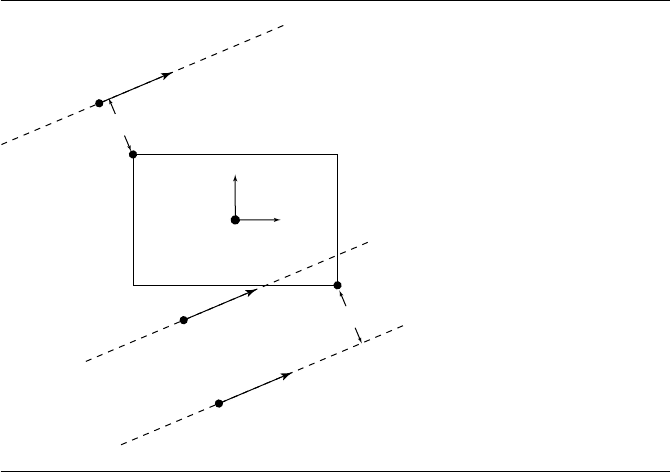
In this case, the transformed line is perpendicular to only one of the basis vectors.

Figure 10.49 shows a line that is perpendicular to the z-axis; the line may be above,

within, or below the OBB. Note that in this case, if the line does not intersect the

OBB, the closest point is always a corner.

The implementation of this can be highly optimized. Assume for the moment that

the (transformed) line’s direction vector





has only positive components; in this case,

if the line doesn’t intersect the box, then the closest point will be either the upper-left

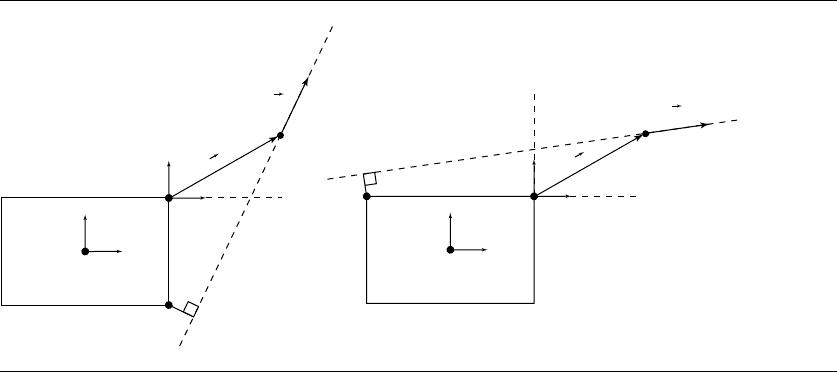
or lower-right corner of the box, as can be seen in Figure 10.49. We can determine

which of these cases is possible by looking at the angle between the vector e going

from the upper-right corner to the line’s origin and the line’s direction vector





.The

Kross function discussed in Section 7.1 can be applied to these two vectors in order to

determine whether the angle between them is positive or negative; if Kross(e,





)>0,

then the line will intersect the “x-axis”; otherwise it will intersect the “y-axis.” In the

former case, the closest point on the box (if no intersection occurs) will be at the

lower-right corner, and in the latter case, the closest point will be at the upper-left

corner. Figure 10.50 demonstrates this. Once this has been determined, we need to

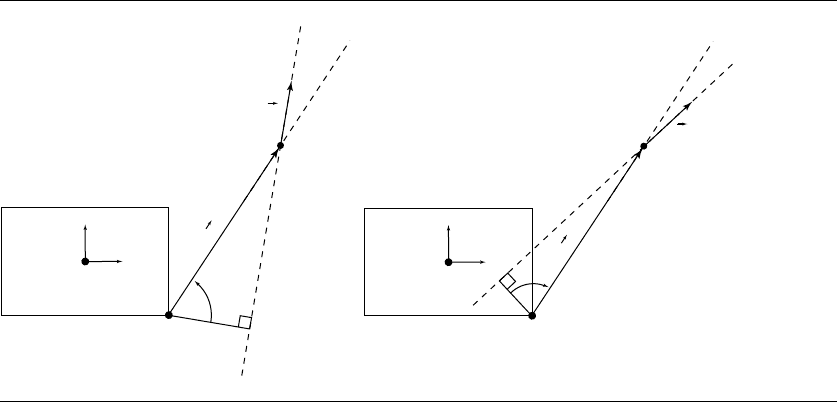
determine whether or not the line intersects the box. Consider the case where the

lower-right corner may be the closest point: If the angle between the line and a vector

from the closest corner to the line’s origin is positive, then the line will not intersect

the box; if the angle is negative, the line will intersect the box. Taking the dot product

of these vectors will not work, as the cosine function is symmetric about 0; however,

we can use the Kross function on the “perp” of the line and the corner-to-line-origin

vector, as shown in Figure 10.51. If the line intersects the box, then its distance is

0; otherwise, the distance squared is the distance between Q



and the transformed

line.

456 Chapter 10 Distance in 3D

dist = 0

dist

Figure 10.49 Case of one zero-component.

The pseudocode is

real CaseOneZeroComponent_Z(Line line, OBB box, real t0, Point qPrime)

{

Vector3D ptMinusExtents = line.origin - box.extents;

real prod0 = line.direction.y * ptMinusExtents.x;

real prod1 = line.direction.x * ptMinusExtents.y;

real distanceSquared = 0;

qPrime.z = line.origin.z;

if (prod0 >= prod1) {

// line intersects ‘‘x-axis’’ of OBB

// Closest point is along bottom edge of right face of OBB

qPrime.x = box.extent.x;

real tmp = line.origin.y + box.extents.y;

delta = prod0 - line.direction.x * tmp;

if (delta >= 0) {

// There is no intersection, so compute distance

10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 457

(ext

, ext

)(ext

, ext

)

Figure 10.50 Determining where to look for the closest point on the box.

invLSquared=1/(line.direction.x * line.direction.x +

line.direction.y + line.direction.y);

distanceSquared += (delta * delta) * invLSquared;

// If desired, compute the parameter of the line’s closest

// point, and set the closest point on the box to be along

// the lower-right edge.

qPrime.y = -box.extents.y;

t0 = -(line.direction.x * ptMinusExtents.x * line.direction.y + tmp)

* invLSquared;

} else {

// Line intersects box. Distance is zero.

inv=1/line.direction.x;

qPrime.y = line.origin - (prod0 * inv);

t0 = -ptMinusExtents.x * inv;

}

} else {

// line intersects the ‘‘y-axis’’ of OBB

// Closest point is along top edge of left face of OBB

// (or, equivalently, left edge of top face)

// Code exactly parallels that above...

}

458 Chapter 10 Distance in 3D

Figure 10.51 Determining whether the line intersects the box.

// Now, consider the z-direction

if (line.origin.z < -box.extents.z) {

delta = line.origin.z + box.extents.z;

distanceSquared += delta * delta;

qPrime.z = -box.extents.z;

} else if (line.origin.z > box.extents.z) {

delta = line.origin.z - box.extents.z;

distanceSquared += delta * delta;

qPrime.z = box.extents.z;

}

return distanceSquared;

}

No Zero-Components

In this case, the transformed line is not parallel to any of the basis vectors. We can,

however, use the Kross operator as we did in the “one zero-component” case and

also assume that all of the transformed line’s components are positive; by doing so,

we can determine which plane the line intersects ﬁrst and exploit this knowledge in

determining intersection with, or distance from, the faces of the box.

10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 459

The pseudocode for this is

real CaseNoZeroComponents(Line line, OBB box, real t, Point qPrime)

{

Vector3D ptMinusExtents = line.origin - box.extents;

real dyEx = line.direction.y * ptMinusExtents.x;

real dxEy = line.direction.x * ptMinusExtents.y;

if (dyEx >= dxEy) {

real dzEx = line.direction.z * ptMinusExtents.x;

real dxEz = line.direction.x * ptMinusExtents.z;

if (dzEx >= dxEz) {

// line intersects x = box.extent.x plane

distanceSquared = FaceX(line, box, ptMinusExtents, t, qPrime);

} else {

// line intersects z = box.extent.z plane

distanceSquared = FaceZ(line, box, ptMinusExtents, t, qPrime);

}

} else {

real dzEy = line.direction.z * ptMinusExtents.y;

real dyEz = line.direction.y * ptMinusExtents.z;

if (dzEy >= dyEz) {

// line intersects y = box.extent.y plane

distanceSquared = FaceY(line, box, ptMinusExtents, t, qPrime);

} else {

// line intersects z = box.extent.z plane

distanceSquared = FaceZ(line, box, ptMinusExtents, t, qPrime);

}

return distanceSquared;

}

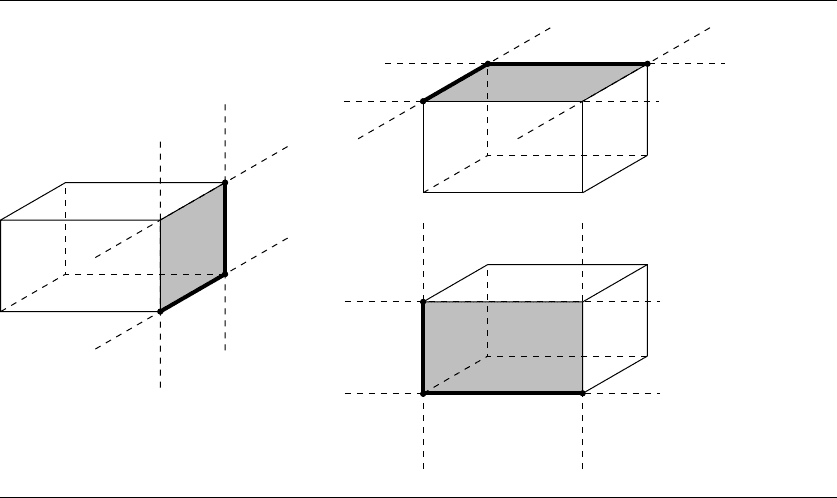
Figure 10.52 shows each “positive” face, against which we test for intersection and

distance. The line intersects the plane of the face (it may or may not intersect the

face itself). Because all the components of the line’s direction vector



d are positive,

it is not possible for the line to be closest to two of the four edges of the face (in the

diagram, the potential “closest” edges are shown with thicker lines). Thus, we are only

interested in six of the nine possible regions deﬁned by the edges of the face.

460 Chapter 10 Distance in 3D

345

Figure 10.52 Each “positive” face of the OBB has two edges and three vertices that may be closest to

the line.

The pseudocode for the face-testing routine for the “positive” X face is as follows:

real Face_X(Line line, OBB box, Vector3D ptMinusExtents, real t, Point3D qPrime)

{

Point3D qPrime = line.origin;

real distanceSquared = 0;

Vector3D ptPlusExtents = line.origin + box.extents;

if (line.direction.x * ptPlusExtents.y >= line.direction.y * ptMinusExtents.x) {

// region 0, 5, or 4

if (line.direction.x * pPe.z >= line.direction.z * ptMinusExtents.x) {

// region 0 - line intersects face

qPrime.x = box.extents.x;

inverse = 1.0 / line.direction.x;

qPrime.y -= line.direction.y * ptMinusExtents.x * inverse;

10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 461

qPrime.z -= line.direction.z * ptMinusExtents.x * inverse;

t = -ptMinusExtents * inverse;

} else {

// region 4 or 5

lSqr = line.direction.x * line.direction.x

+ line.direction.z * line.direction.z;

tmp = lSqr * ptPlusExtents.y - line.direction.y

* (line.direction.x * ptMinusExtents.x + line.direction.z

* ptPlusExtents.z);

if (tmp <= 2 * lSqr * box.extents.y) {

// region 4

tmp = ptPlusExtents.y - (tmp / lSqr);

lSqr += line.direction.y * line.direction.y;

delta = line.direction.x * ptMinusExtents.x + line.direction.y * tmp

+ line.direction.z * ptPlusExtents.z;

t = -delta / lSqr;

distanceSquared += ptMinusExtents.x * ptMinusExtents.x

+ tmp * tmp

+ ptPlusExtents.z * ptPlusExtents.z

+ delta * t;

qPrime.x = box.extents.x;

qPrime.y=t-box.extents.y;

qPrime.z = -box.extents.z;

} else {

// region 5

lSqr += line.direction.y * lineDirection.y;

delta = line.direction.x * ptMinusExtents.x

+ line.direction.y * ptMinusExtents.y

+ line.direction.z * ptPlusExtents.z;

t = -delta / lSqr;

distanceSquared += ptMinusExtents.x * ptMinusExtents.x

+ ptMinusExtents.y * ptMinusExtents.y

+ ptPlusExtents.z * ptPlusExtents.z

+ delta * t;

qPrime.x = box.extents.x;

qPrime.y = box.extents.y;

462 Chapter 10 Distance in 3D

qPrime.z = -box.extents.z;

}

} else {

if (line.direction.x * ptPlusExtents.z >= line.direction.z * ptMinusExtents.x)

// region 1 or 2

lSqr = line.direction.x * line.direction.x + line.direction.y

* line.direction.y;

tmp = lSqr * ptPlusExtents.z - line.direction.z * (line.direction.x

* ptMinusExtents.x + line.direction.i1 * ptPlusExtents.y);

if (tmp <= 2 * lSqr * box.extents.z) {

// region 2

tmp = ptPlusExtents.z - (tmp / lSqr);

lSqr += line.direction.z * line.direction.z;

delta = line.direction.x * ptMinusExtents.x + line.direction.y

* ptPlusExtents.y + line.direction.z * tmp;

t = -delta / lSqr;

distanceSquared += ptMinusExtents.x * ptMinusExtents.x

+ ptMinuxExtents.y * ptMinusExtents.y

+ tmp * tmp

+ delta * t;

qPrime.x = box.extents.x;

qPrime.y = -box.extents.y;

qPrime.z=t-box.extents.z;

} else {

// region 1

lSqr += line.direction.z * lineDirection.z;

delta = line.direction.x * ptMinusExtents.x

+ line.direction.y * ptMinusExtents.y

+ line.direction.z * ptPlusExtents.z;

t = -delta / lSqr;

distanceSquared += ptMinusExtents.x * ptMinusExtents.x

+ ptPlusExtents.y * ptPlusExtents.y

+ ptMinusExtents.z * ptMinusExtents.z

+ delta * t;

qPrime.x = box.extents.x;

10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 463

qPrime.y = -box.extents.y;

qPrime.z = box.extents.z;

}

} else {

lSqr = line.direction.x * line.direction.x +

line.direction.z * line.direction.z;

tmp = lSqr * ptPlusExtents.y - line.direction.y * (line.direction.x

* ptMinusExtents.x + line.direction.z * ptPlusExtents.z);

if (tmp >= 0) {

// region 4 or 5

if (tmp <= 2 * lSqr * box.extents.y) {

// region 4. Code block same as previous region 4 code.

} else {

// region 5. Code block same as previous region 5 code.

}

lSqr = line.direction.x * line.direction.x + line.direction.y

* line.direction.y;

tmp = lSqr * ptPlusExtents.z

- line.direction.z * (line.direction.x * ptMinusExtents.x

+ line.direction.y * ptPlusExtents.y);

if (tmp >= 0) {

// region 1 or 2

if (tmp <= 2 * lSqr * box.extents.z) {

// Region 2. Code block same as previous region 2 code.

} else {

// Region 1. Code block same as previous region 1 code.

}

return distanceSquared;

}