Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

444 Chapter 10 Distance in 3D

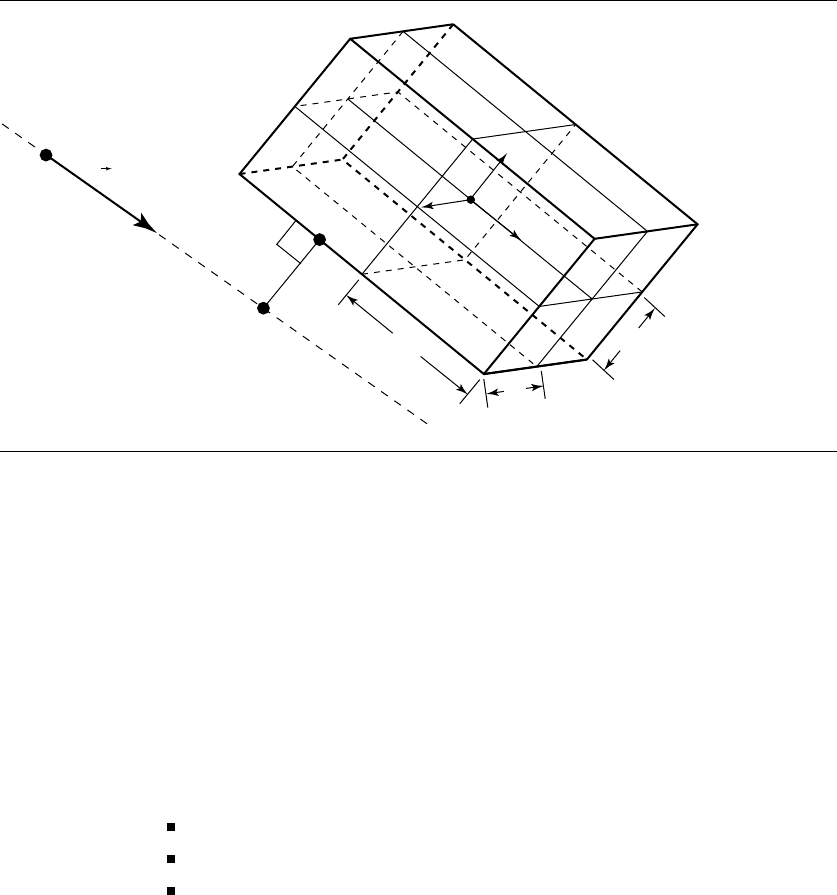
Figure 10.43 The partitioning of the solution domain for a line segment and rectangle.

For each type of linear component, the ﬁrst step is to ﬁnd the determinant of

the system, and if it is nonzero, to then compute the solution in order to ﬁnd the

region in which the solution lies. Once the region has been determined, calculations

speciﬁc to that region are made in order to ﬁnd the point ( ¯u, ¯v,

t) on the boundary

that represents the minimum.

For the case of the line and rectangle distance, the domain is partitioned into an

inﬁnite square column, which deﬁnes nine regions. The pseudocode for ﬁnding the

region in which the unconstrained solution lies is

float LineRectangleDistanceSquared(Line line, Rectangle rectangle)

{

// Convert to parametric representation

// Assumes rectangle vertices are ordered counterclockwise

V = rectangle.V[0];

e0 = rectangle.V[1] - V;

e1 = rectangle.V[3] - V;

a00 = Dot(e0, e0);

a01 = Dot(e0, e1);

a02 = -Dot(e0, line.direction);

a11 = Dot(e1, e1);

a12 = -Dot(e1, line.direction);

a22 = Dot(line.direction, line.direction);

diff=V-line.base;

10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 445

b0 = Dot(e0, diff);

b1 = Dot(e1, diff);

b2 = Dot(line.direction, diff);

c = Dot(diff, diff);

// Cofactors to be used for determinant

// and inversion of matrix A

cof00 = a11 * a22 - a12 * a12;

cof01 = a02 * a12 - a01 * a22;

cof02 = a01 * a12 - a02 * a11;

det = a00 * cof00 + a01 * cof01 + a02 * cof02;

// Flip determinant and b, to avoid

// special cases later

if (det < 0) {

det = -det;

b0 = -b0;

b1 = -b1;

b2 = -b2;

}

// Check for (near) parallelism

if (det < epsilon) {

// Line and rectangle are parallel.

// Find the closest points by computing

// the distance between the line to

// the segment defining each edge and

// taking the minimum.

Segment seg0 = { rectangle[0], rectangle[1] };

float dist0 = LineLineSegmentDistanceSquared(line, seg0);

Segment seg1 = { rectangle[1], rectangle[2] };

float dist1 = LineLineSegmentDistanceSquared(line, seg1);

Segment seg2 = { rectangle[2], rectangle[3] };

float dist2 = LineLineSegmentDistanceSquared(line, seg2);

Segment seg3 = { rectangle[3], rectangle[0] };

float dist3 = LineLineSegmentDistanceSquared(line, seg3);

return (MIN(seg0, MIN(seg1, MIN(seg2, seg3))));

}

// Compute u, v

446 Chapter 10 Distance in 3D

cof11 = a00 * a22 - a02 * a02;

cof12 = a02 * a01 - a00 * a12;

u = -(cof00 * b0 + cof01 * b1 + cof02 * b2);

v = -(cof01 * b0 + cof11 * b1 + cof12 * b2);

if(s<0){

if(t<0){

region 6;

} else if (t <= det) {

region 5;

} else {

region 4;

}

} else if (s <= det) {

if(t<0){

region 7;

} else if (t <= det) {

region 0;

} else {

region 3;

}

} else {

if(t<0){

region 8;

} else if (t <= det) {

region 1;

} else {

region 2;

}

The code for the various regions is implemented in exactly the way that the line-

to-triangle code is built.

Ray to Rectangle and Line Segment to Rectangle

The basic approach for the ray/rectangle and segment/rectangle distance problems is

exactly analogous to that just presented for line/rectangle distance. However, in the

former case, instead of having 9 regions in the domain, we have 18 (the same 9 as

for the line/rectangle case, but doubled because the ray divides its inﬁnite line into

2 regions—t<0 and t ≥ 0); in the latter case, we have 27 regions—three sets of the

same 9 for t<0, 0 ≤ t ≤ 1, and t>1.

10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 447

Figure 10.44 Distance between a line and a tetrahedron.

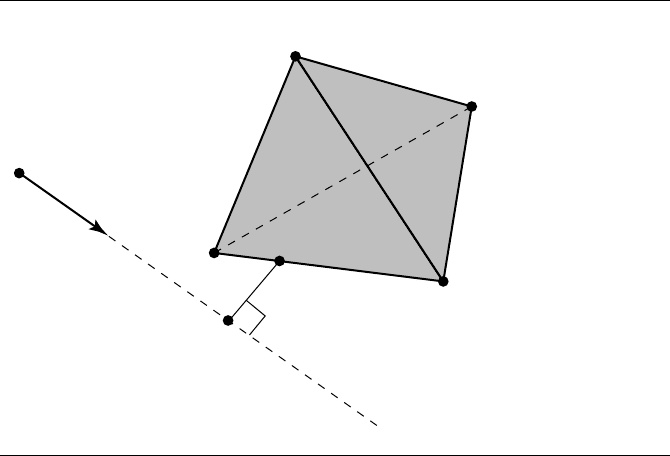
10.9.3 Linear Component to Tetrahedron

In this section we discuss the problem of computing the distance from a linear com-

ponent to a tetrahedron, as shown in Figure 10.44. Let V

,0≤i ≤3, be the vertices of

the tetrahedron. The linear component is P + t

d,where

d is a unit-length vector and

t ∈ R (line), t ≥ 0 (ray), or t ∈ [0, T ] (segment). The construction can be modiﬁed

slightly to handle

d that is not unit length. The tetrahedron can be parameterized by

+ s

e

+ s

e

+ s

e

,wheree

= V

− V

, s

≥ 0, and s

+ s

≤ 1.

Distance

Translate the tetrahedron and line by subtracting P . The tetrahedron vertices are

now V

= U

− P for all i. The line becomes s

d. Project onto the plane containing

the origin O and having normal

d; Figure 10.45(a) shows this projection (in 2D for

clarity). The projected line is the single point O. The projected tetrahedron vertices

are W

= (I −

for all i. The boundary of the projected solid tetrahedron is a

convex polygon, either a triangle or a quadrilateral. If the convex polygon contains

O, the distance from the line to the tetrahedron is zero. Otherwise, the distance

from the line to the tetrahedron is the distance from O to the convex polygon. The

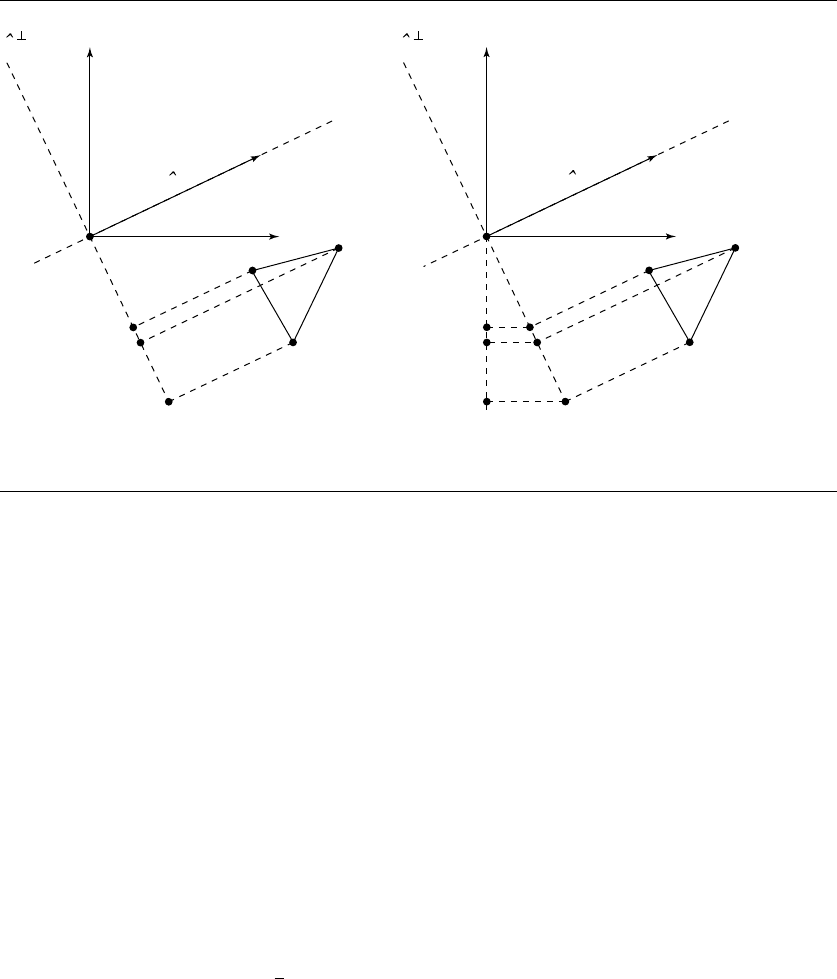
448 Chapter 10 Distance in 3D

d d

(a) (b)

Figure 10.45 Projecting a tetrahedron (a) onto a plane perpendicular to

d and then (b) into 2D.

projected values are in a plane in 3D and can be projected into 2D with the standard

technique of eliminating the coordinate corresponding to the maximum absolute

component of

d, as shown in Figure 10.45(b). The distance between a point and a

convex polygon can be computed in 2D. This value must be adjusted to account for

the 3D-to-2D projection. For example, if

d = (d

, d

) with |d

|=max

{|d

|} and

r is the computed 2D distance, then the 3D distance is r/d

Closest Points

The set of tetrahedron points closest to the line in many cases consists of a single

point. In other cases, the set can consist of a line segment of points. For example, con-

sider the tetrahedron with vertices (0, 0, 0), (1, 0, 0), (0, 1, 0), and (0, 0, 1). The line

(1/4, 1/4, 0) +t(0, 0, 1) intersects the tetrahedron for t ∈ [0, 1/2], so the correspond-

ing points are zero units of distance from the tetrahedron. The line (−1, −1, 1/2) +

t(0, 0, 1) is

√

2 units of distance from the tetrahedron. The closest points on the line

are generated by t ∈ [0, 1/2], and the closest points on the tetrahedron are (0, 0, t)for

the same interval of t values. The line (1/2, −1/2, 0) +t(0, 0, 1) is 1/2 units of distance

10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 449

from the tetrahedron. The closest points on the line are generated by t ∈[0, 1/2], and

the closest points on the tetrahedron are (1/2, 0, t) for the same interval of t values.

Case 1 Let O be strictly inside the convex polygon. In this case, the line intersects the tetra-

hedron in an interval of points. Let E = [e

e

] be the matrix whose columns are

the speciﬁed edge vectors of the tetrahedron. Let s be the 3 ×1 vector whose com-

ponents are the s

parameters. The line segment of intersection is t

d + P = Es + V

for t ∈ [t

min

, t

max

].Theproblemnowistocomputethet-interval. The edge vectors

of the tetrahedron are linearly independent, so E is invertible. Multiplying the vector

equation by the inverse and solving for the tetrahedron parameters yields

s = E

−1



d + P − V



=at +



where a = (a

, a

) = E

−1

d and



b = (b

, b

) = E

−1

(P − V

). The parameters

s must satisfy the inequality constraints for the tetrahedron. The parameter t is

therefore constrained by the four inequalities:

t + b

≥ 0, a

t + b

≥ 0, a

t + b

≥ 0, (a

+ a

)t + (b

+ b

) ≤ 1

Each of these inequalities deﬁnes a semi-inﬁnite interval of the form [

t, ∞) or

(−∞,

t]. In this particular case, we know the intersection of the four intervals must

be nonempty and of the form [t

min

, t

max

The division required to compute E

−1

can be avoided. Let us assume that the

tetrahedron is oriented so that det(E)>0. Multiply by the adjoint E

adj

to obtain

det(E)s = E

adj



d + P − V



=αt +



The four t-inequalities are of the same form as earlier, but where a

refers to the

components of α, b

refers to the components of



β, and the last inequality becomes a

comparison to det(E) instead of to 1.

Case 2 Let O be on the convex polygon boundary or outside the polygon. Let C be the

closest polygon point (in 3D) to O. The line t

d + C intersects the tetrahedron with

vertices either in a single point or in an interval of points. The method in Case

1 may be used again, but now you need to be careful with the interval construction

when using ﬂoating-point arithmetic. If the intersection is a single point, theoretically

min

= t

max

, but numerically you might wind up with an empty intersection. It is not

difﬁcult to trap this and handle appropriately. Observe that Cases 1 and 2 are handled

by the same code since in Case 1 you can choose C =O.

450 Chapter 10 Distance in 3D

Ray and Tetrahedron

Use the line-tetrahedron algorithm for computing the closest line points with param-

eters I =[t

min

, t

max

](with possibly t

min

max

). Deﬁne J =I ∩[0, ∞).IfJ =∅, the

ray-tetrahedron distance is the same as the line-tetrahedron distance. The closest ray

points are determined by J .IfJ =∅, the ray origin P is closest to the tetrahedron.

Segment and Tetrahedron

Use the line-tetrahedron algorithm for computing the closest line points with pa-

rameters [t

min

, t

max

] (with possibly t

min

= t

max

). Deﬁne J =I ∩ [0, T ]. If J =∅, the

segment-tetrahedron distance is the same as the line-tetrahedron distance. The clos-

est segment points are determined by J .IfJ =∅, the closest segment point is P when

max

< 0orP + T

d when t

min

>T.

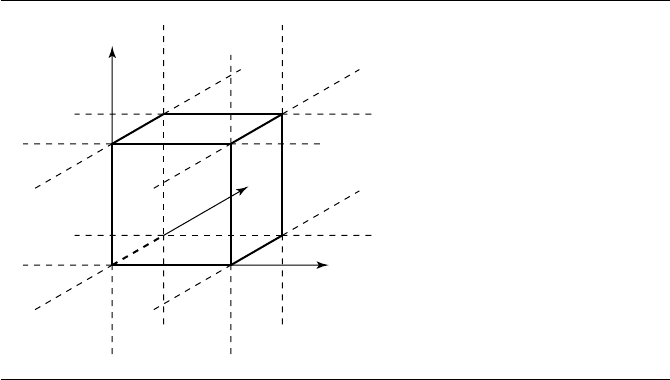
10.9.4 Linear Component to Oriented Bounding Box

In this section we discuss the problem of computing the distance between a linear

component and an oriented bounding box (OBB). A linear component is deﬁned as

a base point and a direction vector:

L(t) = P + t



An OBB is deﬁned as a centerpoint C; three orthonormal orientation vectors ˆu, ˆv,

and ˆw; and three half-extents h

, h

, and h

, as shown in Figure 10.46.

The naive approach would compute the squared distance between the line and

each of the six faces and take the minimum of these; however, this would be quite

expensive because of the arbitrary orientation of the faces and also would fail to

exploit the fact that each face is parallel or orthogonal to every other face.

The approach we take here is analogous to that taken for the problem of comput-

ing the distance of a point to an OBB, as described in Section 10.4.2.

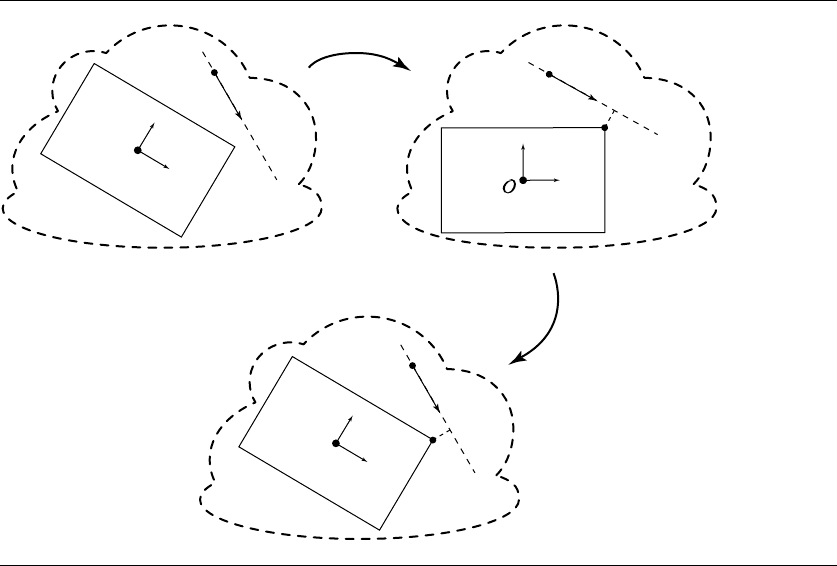
The OBB’s centerpoint C and ˆu, ˆv, and ˆw deﬁne a frame. Observe that, relative

to that frame, the OBB is an axis-aligned box centered at the origin, whose sides are

each parallel to either the x-, y-, or z-axis. If we transform the line {P ,



d} into this

frame, then we can exploit this axis-aligned, origin-centered nature of the OBB and

compute the closest point, and the distance to it, more efﬁciently.

Given the OBB’s center C and ˆu, ˆv, and ˆw, a point P ’s coordinates in that frame

can be computed as



[

(P − C) ·ˆu(P− C) ·ˆv(P− C) ·ˆw

]

10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 451

Figure 10.46

Distance between a line and an oriented bounding box.

That is, we simply project the vector between the P and C onto each of the OBB’s

basis vectors. Note that this is functionally equivalent to creating a transform T from

global space into the local space of the OBB with matrix

T =



ˆu

ˆv

ˆw



−C 1



and multiplying by P , but is more efﬁcient. The same process may be applied to



the direction vector for the line.

Once inside the frame of the OBB, we can compute three things:

The coordinates of the closest point on the OBB to the line.

The parameter of the point on the line closest to the OBB.

The squared distance between the OBB and the line.

(Note that, of course, if the line intersects the OBB, then the distance is 0, and the

other two pieces of information are moot.)

The coordinates of the closest point on the OBB are found in a frame whose

origin is [

000

] and whose basis vectors are orthonormal. Because of this, we

452 Chapter 10 Distance in 3D

P' = T(P)

–1

Figure 10.47 Schematic for line-OBB distance algorithm.

can view these coordinates as parameter values of the closest point on the OBB, in

the untransformed frame. If we want the actual location of the closest point in that

frame, we simply have to compute the following:

Q = C + Q



ˆu + Q



ˆv + Q



ˆw

Of course, the parameter of the point on the transformed line can simply be applied

to the untransformed line, in order to ﬁnd the actual point (if this is desired) in the

untransformed frame. Figure 10.47 shows a schematic of this process (shown in 2D

for clarity).

Once the line has been transformed into the OBB’s local frame, we can exploit

the fact that the faces are all parallel to the basis vectors of the frame. Certainly, it is

more efﬁcient to compute intersections and distances when the “target” is parallel to

a basis vector, but we exploit this even further by breaking down the conﬁgurations

into several cases, to which we apply an algorithm that computes only the minimum

necessary for each case.

10.9 Linear Component to Triangle, Rectangle, Tetrahedron, Oriented Box 453

The conﬁgurations are categorized by looking at the (now-transformed) direc-

tion vector





of the line L. Speciﬁcally, we look for how many components of





are zero—there may be none, one, two, or three. We discuss these cases in order of

increasing complexity.

For the cases of zero, one, or two zero-components, we employ a bit of a “trick” in

the implementation. We consider the values of the components of





:ifacomponent

is negative, we ﬂip its sign and ﬂip the sign of the corresponding component of P



We then proceed with the rest of the algorithm, and then ﬂip the corresponding

components of the resulting nearest point on the OBB (this works because the OBB

is symmetric about the origin in all three dimensions). This ensures that all the

components of





are nonnegative, which reduces the number of cases we have to

consider.

Three Zero-Components

In this case, the line is simply a point, and the problem degenerates into ﬁnding the

distance from a point to an axis-aligned box, the solution to which may be found in

Section 10.4.2.

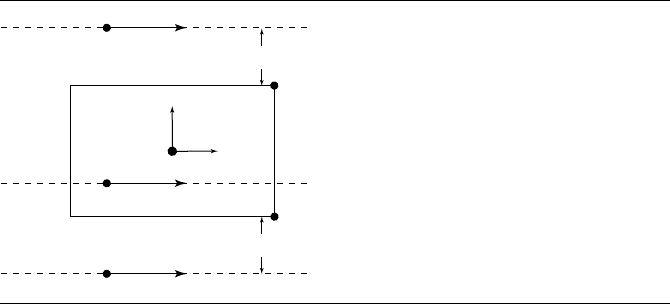
Two Zero-Components

In this case, the transformed line is perpendicular to two of the basis vectors and

parallel to the third. Figure 10.48 shows a line that is perpendicular to the y- and

z-axes of the OBB; the line may be above, within, or below the OBB.

dist

dist = 0

dist

Figure 10.48 Case of two zero-components.