Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

484 Chapter 11 Intersection in 3D
The pseudocode for line-plane intersection is
boolean LineIntersectPlane(
Line3D line,
Plane plane,
float& t,
Point3D& intersection)
{
// Check for (near) parallel line and plane
denominator = Dot(line.direction, plane.normal)
if (Abs(denominator) < epsilon) {
// Check if line lies in the plane or not.
// We do this, somewhat arbitrarily, by checking if
// the origin of the line is in the plane. If it is,
// set the parameter of the intersection to be 0. An
// application may wish to handle this case differently...
if (Abs(line.origin.x * plane.a + line.origin.y * plane.b +
line.origin.z * plane.c + plane.d) < epsilon) {
t=0;
return (true);
} else {
return false;
}
}
// Nonparallel, so compute intersection
t = -(plane.a * line.origin.x + plane.b * line.origin.y +
plane.c * line.origin.z + plane.d);
t=t/denominator;
intersection = line.origin+t*line.direction;
return true
}
Ray-Plane Intersection
A ray is only defined for t ≥ 0, so we can simply check if the t value calculated by
the line intersection routine is greater than or equal to 0, and accept or reject the
intersection.
Line Segment–Plane Intersection
We assume a line segment is represented by a pair of points {P
0
, P
1
}. We can again
employ a similar algorithm for line-plane intersection by converting the line segment
into ray form:
11.1 Linear Components and Planar Components 485
R(t) = P
0
+ t(P
1
− P
0
)
The segment is defined for 0 ≤ t ≤ 1, and so we can simply compare the t-value
computed to that range, and accept or reject the intersection.
11.1.2 Linear Components and Triangles
In this section, we’ll cover intersections of rays, lines, and line segments with trian-
gles. In a subsequent section, we’ll be covering the more general case of the intersec-
tion of linear components and polygons; it certainly would be possible to simply solve
the line/triangle intersection problem as a special case of a three-vertex polygon, but
we can exploit barycentric coordinates and come up with a more direct and efficient
solution.
One approach is to intersect the linear component with the plane containing
the triangle, and then determine whether or not the intersection point is within the
triangle. The determination of containment can be done by simply projecting the
triangle’s vertices and the point of intersection onto one of the axis-aligned planes
(choosing the plane that maximizes the area of the projected triangle), and then
using a 2D point-in-triangle test (see Haines 1994 and Section 13.3.1). However,
such an approach requires either computing the normal of the triangle every time
an intersection test is done or storing the normal (and making sure it’s recomputed
if and when it changes).
An alternative is to use an approach due to M
¨
oller and Trumbore (1997). We’ll
again consider a linear component defined as an origin and direction vector (Equa-
tion 11.1). A triangle is defined simply as a sequence of vertices {V
0
, V
1
, V
2
} (see
Figure 11.2).
To review, any point in a triangle can be defined in terms of its position relative
to the triangle’s vertices:
Q
u,v,w
= wV
0
+ uV
1
+ vV
2
(11.5)
where u + v + w = 1. The triple (u, v, w) is known as the barycentric coordinates
of Q, although since w = 1 − (u + v), frequently just the pair (u, v) is used (see
Section 3.5).
As with the linear component–plane intersection, we can compute the linear
component–triangle intersection by simply substituting Equation 11.2 into Equa-
tion 11.5:
P + t
ˆ
d = (1 − (u + v))V
0
+ uV
1
+ vV
2
which can be expanded to
[
−
ˆ
dV
1
− V
0
V
2
− V
0
]
t
u
v
=
[
P − V
0
]
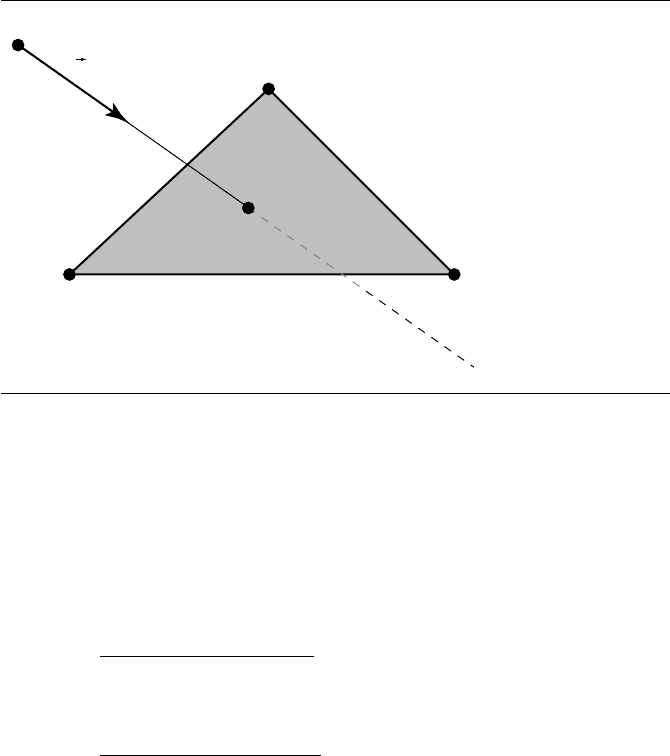
486 Chapter 11 Intersection in 3D
P
Q
V
0
V
1
V
2
d
Figure 11.2 Intersection of a line and a triangle.
Recalling that each of these variables are vector-valued, you can see that this is a three-
equation linear system, with three unknowns. There are any number of ways to solve
this, but here we choose to use Cramer’s rule (see Sections 2.7.4 and A.1).
By Cramer’s rule, we have
t
u
v
=
1
|
−
ˆ
dV
1
− V
0
V
2
− V
0
|
|P − V
0
V
1
− V
0
V
2
− V
0
|
|−
ˆ
dP− V
0
V
2
− V
0
|
|−
ˆ
dV
1
− V
0
P − V
0
|
=
1
(
ˆ
d × (V
2
− V
0
)) · (V
1
− V
0
)
((P − V
0
) × (V
1
− V
0
)) · (V
2
− V
0
)
(
ˆ
d × (V
2
− V
0
)) · (P −V
0
)
((P − V
0
) × (V
1
− V
0
)) ·
ˆ
d
This last rewriting is due to the fact that
|
u v w
|
=−(u ×w) ·v
=−( w ×v) ·u
and was done to expose the common subexpressions
ˆ
d × (V
2
−V
0
) and (P − V
0
) ×
(V
1
− V
0
).
Once we solve for t, u, and v, we can determine whether the intersection point
is within the triangle (rather than somewhere else in the plane of the polygon) by
11.1 Linear Components and Planar Components 487
inspecting their values: if 0 ≤u ≤ 1, 0 ≤ v ≤ 1, and u + v ≤1, then the intersection
is within the triangle; otherwise, it is in the plane of the polygon, but outside the
triangle.
The pseudocode for this is
bool LineTriangleIntersect(
Triangle3D tri,
Line3D line,
Isect& info,
float epsilon,
Point3D& intersection)
{
// Does not cull back-facing triangles.
Vector3D e1, e2, p, s, q;
float t, u, v, tmp;
e1 = tri.v1 - tri.v0;
e2 = tri.v2 - tri.v0;
p = Cross(line.direction, e2);
tmp = Dot(p, e1);
if (tmp > -epsilon && tmp < epsilon) {
return false;
}
tmp = 1.0 / tmp;
s = line.origin - tri.v0;
u = tmp * Dot(s, p);
if (u < 0.0 || u > 1.0) {
return false;
}
q = Cross(s, e1);
v = tmp * Dot(d, q);
if (v < 0.0 || v > 1.0) {
return false;
}
t = tmp * Dot(e2, q);
info.u = u;
info.v = v;
info.t = t;
488 Chapter 11 Intersection in 3D
intersection = line.origin+t*line.direction;
return true;
}
Ray-Triangle Intersection
A ray is only defined for t ≥ 0, so we can simply check if the t valuecomputedis
nonnegative, and accept or reject the intersection.
Line Segment–Triangle Intersection
We assume a line segment is represented by a pair of points {P
0
, P
1
}. We can again em-
ploy a similar algorithm for line-triangle intersection by converting the line segment
into line form. The segment is defined for 0 ≤t ≤ 1, and so we can simply compare
the t-value to that range, and accept or reject the intersection.
11.1.3 Linear Components and Polygons
Computation of intersections between linear components and triangles was aided
by our ability to specify the point of intersection in barycentric coordinates; the
intersection was guaranteed (within floating-point error) to be in the plane of the
triangle. Unfortunately, this trick cannot be directly exploited for polygons in general.
For polygons that are not self-intersecting, it is theoretically possible to triangulate
them, and then apply the linear component–triangle intersection algorithm on each
triangle, but this is likely not efficient.
In the following sections, the polygons are assumed to be planar within floating-
point error, non-self-intersecting, closed, and consisting of a single contour. Polygons
are represented by a list of n vertices: {V
0
, V
1
, ..., V
n−1
}. The plane of the polygon is
implied by the vertices and represented in the usual fashion as a normal and distance
from the origin: ax +by + cz + d = 0, where a
2
+ b
2
+ c
2
= 1.
Because we cannot (in general) exploit the “barycentric coordinates trick” we
used for triangles, linear component–polygon intersection requires several steps:
1. Compute the plane equation for the polygon. This can be done by selecting an
arbitrary vertex as a point on the plane and then computing the normal using
the cross product of the vectors formed by that vertex and its neighbors; however,
in general polygons are not exactly planar, so a more robust mechanism, such
as Newell’s method (Tampieri 1992) or the hyperplanar fitting of Section A.7.4
should be employed.
2. Compute the intersection of the linear component with the plane (see Sec-
tion 11.1.1).
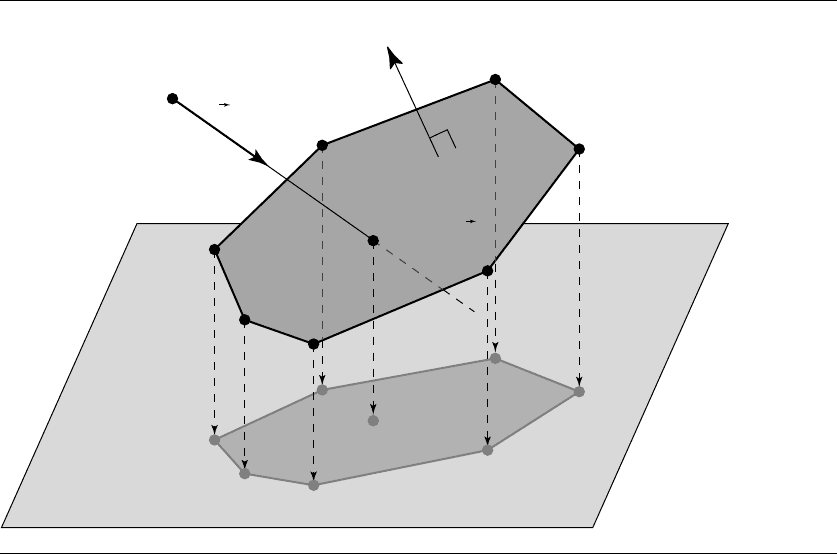
11.1 Linear Components and Planar Components 489
P
Q = P + td
V
0
V
1
V
2
V
3
V
4
V
5
V
6
V'
0
V'
1
V'
2
V'
3
V'
4
V'
5
V'
6
Q'
XZ plane
nˆ
d
Figure 11.3 Intersectionofarayandapolygon.
3. If the linear component intersects the polygon’s plane, determine whether the
intersection point is within the boundaries of the polygon.
This last step corresponds to the inspection of the barycentric coordinates for the
ray/triangle intersection, but for polygons we must employ a “trick.” This trick con-
sists of projecting the polygon’s vertices and the intersection point Q onto one of
the planes defined by the local frame (the XY , YZ,orXZ planes) and then deter-
mining whether the projected intersection point Q
lies within the projected polygon
{V
0
, V
1
, ..., V
n−1
} (see Figure 11.3).
As the projection we desire is orthographic, the projection step consists of
choosing one coordinate to ignore and using the other two coordinates as (x, y)
coordinates in a two-dimensional space. The coordinate to ignore should be the one
that shows minimal variance across the vertices of the polygon; that is, if we compute
a bounding box, the rejected coordinate should be the one that corresponds to the
shortest side of the box. By doing this, numerical errors due to the projection are
minimized, particularly when the polygon is very nearly coplanar with one of the
orthogonal planes.
490 Chapter 11 Intersection in 3D
So, in the final step we simply have to solve a two-dimensional point-in-polygon
problem, for which there are many algorithms (see Section 13.3).
We should note that a polygon may be defined as the intersection of a plane and
a set of half-spaces; these half-spaces are those defined by considering each pair of
vertices {V
i
, V
i+1
}as two points on a plane perpendicular to the plane of the polygon.
We could then determine if the intersection point of the line and the polygon’s plane
was on the same side of all of these half-spaces. This same sort of algorithm could
be employed as the 2D point-in-polygon algorithm the other approach uses, and so
the question arises, “Why project the points if we’re going to use (basically) the same
method?” The answer is efficiency—it’s arguably faster to do it in (projected) 2D.
The pseudocode for this is
bool LinePolygonIntersection(
Polygon3D poly,
Line3D line,
float& t,
Point3D& intersection)
{
// lcp direction is assumed to be normalized
// Also assumes polygon is planar
Vector3D N, p, e1, e2;
float numer, denom;
e1 = poly.vertexPosition(1) - poly.vertexPosition(0);
e2 = poly.vertexPosition(2) - poly.vertexPosition(1);
N = Cross(e1, e2);
N /= N.length();
p = poly.vertexPosition(0);
denom = Dot(line.direction, N);
if (denom < 0) {
numer = Dot(N, p - line.origin);
t = numer / denom;
if(t<0){
return false;
}
p = line.origin+t*r.d;
int projectionIndex = MaxAbsComponent(N);
Point2D* 2dPoints;
Point2D p2d;
2dPoints = new Point2D[poly.numVertices];
// Project Points into a 2D plane
// by removing the coordinate that
// was the fabs maximum in the normal
11.1 Linear Components and Planar Components 491
// return them in array 2dPoints.
Project2D(poly.VertexArray, projectionIndex, 2dPoints,
poly.numVertices);
Project2D(p, projectionIndex, p2d, 1);
// Choose your method of winding test
// Sign of dotProducts etc...
if (PointIn2DPolygon(p2d, 2dPoints)) {
delete [] 2dPoints;
intersection = line.origin+t*line.direction;
return true;
} else {
delete [] 2dPoints;
return false;
}
} else {
// Back facing
return false;
}
}
Ray-Polygon Intersection
A ray is only defined for t ≥ 0, so we can simply check if t is nonnegative, and accept
or reject the intersection.
Line Segment–Polygon Intersection
We assume a line segment is represented by a pair of points {P
0
, P
1
}. We can again
employ a similar algorithm for line-polygon intersection by converting the line seg-
ment into ray form. The segment is defined for 0 ≤t ≤1, and so we can simply check
if t is in that range, and accept or reject the intersection.
11.1.4 Linear Component and Disk
In this section we address the problem of intersecting a linear component with a disk
(see Figure 11.4). The linear component is defined in the usual fashion:
L(t) = P + t
d
and the disk is defined in the same fashion as the 3D circle (see Section 9.2.3):
P = C +r ˆw
θ
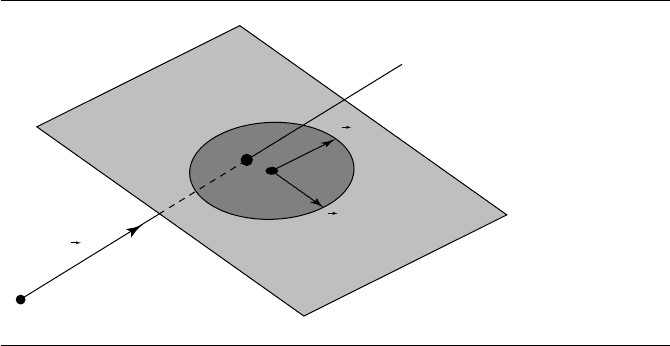
492 Chapter 11 Intersection in 3D
C
P
d
v
u
Figure 11.4 Intersection of a linear component and a disk.
where
ˆw
θ
= cos θ ˆu + sin θ ˆv
A disk is simply a 3D circle that also includes the planar region bounded by the
perimeter of the circle: if a line goes through the “interior” of a circle, no intersection
occurs, but if a line goes through a disk’s interior, an intersection occurs. Alterna-
tively, we can specify it simply as a centerpoint C, a plane normal ˆn,andaradiusr;
however, this loses any parametric information (of the intersection point, relative to
the “axes” of the circle)—this may or may not be relevant to the application.
The algorithm is simply to intersect the linear component with the plane in which
the disk lies, and then to compute the squared distance between the intersection and
the center of the disk, and compare this against the squared radius. If the linear com-
ponent lies within the plane of the disk, then an application may or may not wish to
consider intersections. If intersections in this case are desired, a 3D generalization of
the 2D linear component–circle intersection algorithm may be used; if the applica-
tion is merely interested in whether or not an intersection occurred, then the distance
(squared) from the linear component to the circle can be compared to the (squared)
radius.
The pseudocode is
bool LineIntersectDisk(Line3D line, Disk3D disk, Point3D p)
{
Plane3D plane;
plane.normal = disk.normal;
11.2 Linear Components and Polyhedra 493
plane.p = disk.center;
float t;
Point3D intersection
if (!LinePlaneIntersection(plane, line, t, p)) {
return false;
}
if (DistanceSquared(p, disk.center) <= disk.radius * disk.radius) {
return true;
} else {
return false;
}
}
Ray-Disk Intersection
A ray is only defined for t ≥ 0, so we can simply check if t is nonnegative, and accept
or reject the intersection.
Line Segment–Disk Intersection
We assume a line segment is represented by a pair of points {P
0
, P
1
}. We can again
employ a similar algorithm for line-disk intersection by converting the line segment
into ray form. The segment is defined for 0 ≤t ≤ 1, and so we can simply check if t
is in that range, and accept or reject the intersection.
11.2 Linear Components and Polyhedra
This section addresses the problem of intersecting linear components with polyhedra
and polygonal meshes. The linear components ray, line, and line segment are defined
by an origin point and a vector:
L(t) = P + t
d
In the case of a line segment defined by two points P
0
and P
1
,welet
d = P
1
− P
0
.A
polyhedron is defined as described in Section 9.3. A polygonal mesh, for the purposes
of this section, is simply a polyhedron that is not necessarily closed. Figure 11.5
shows a ray intersecting with an octahedron, while Figure 11.6 shows a line segment
intersecting with a triangle mesh. Note that polyhedra are not required to be regular,
and polygonal meshes are not required to have all triangular faces.
